大問１
１ 次の (1)～(5) の問いに答えよ。
(1) \( 63 \div 9-2 \) を計算せよ。
(2) \( \left( \dfrac{1}{2}-\dfrac{1}{5} \right) \times \dfrac{1}{3} \) を計算せよ。
(3) \( (x+y)^2-x(x+2y) \) を計算せよ。
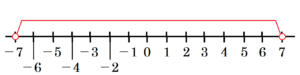
(4) 絶対値が \( 7 \) より小さい整数は全部で何個あるか求めよ。
絶対値が \( 7 \) より小さい整数 \( n \) を不等号を使って表すと，\( -7<n<7 \) となります。
（絶対値が \( 7 \) より小さい なので，\( -7 \) と \( 7 \) は含まれません）
よって，あてはまるのは，\( -6 \) から \( 6 \) までの１３個になります。
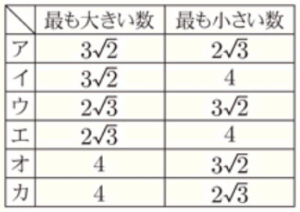
(5) ３つの数 \( 3\sqrt{2}，2\sqrt{3}，4 \) について，最も大きい数と最も小さい数の組み合わせとして正しいものを下のア～カの中から１つ選び，記号で答えよ。
２ 連立方程式 \( \left\{ \begin{array}{}
3x+y=8 \\
x-2y=5 \\ \end{array} \right. \) を解け。
３ １０円硬貨が２枚，５０円硬貨が１枚，１００円硬貨が１枚ある。この４枚のうち，２枚を組み合わせてできる金額は何通りあるか求めよ。
４ \( \dfrac{9}{11} \) を小数で表すとき，小数第２０位を求めよ。
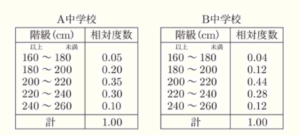
５ 下の２つの表は，Ａ中学校の生徒２０人とＢ中学校の生徒２５人の立ち幅跳びの記録を，相対度数で表したものである。このＡ中学校の生徒２０人とＢ中学校の生徒２５人を合わせた４５人の記録について，\( 200 \; cm \) 以上 \( 220 \; cm \) 未満の階級の相対度数を求めよ。
ここから，Ａ，Ｂ各中学校の\( 200 \; cm \) 以上 \( 220 \; cm \) 未満の階級の度数を求めると，
Ａ中学校 ･･･ \( 0.35 \times 20=7 \)（人）
Ｂ中学校 ･･･ \( 0.44 \times 25=11 \)（人）
となり，両中学校の合計の度数は \( 18 \) 人になります。
【 相対度数 \( = \) 度数 \( \div \) データの総数 】で求められるので，
\( 18 \div 45=0.40 \)
大問２
1 次は，先生と生徒の授業中の会話である。次の (1)～(3) の問いに答えよ。
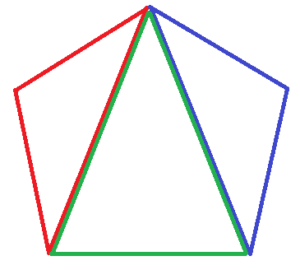
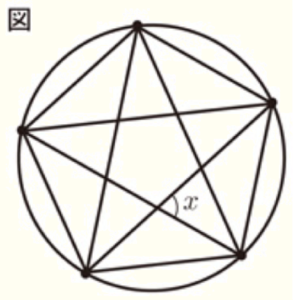
先 生：円周を５等分している５つの点をそれぞれ結ぶと，図のように
なります。図を見て何か気づいたことはありますか。
生徒Ａ：先生，私は正五角形と星形の図形を見つけました。
先 生：正五角形と星形の図形を見つけたんですね。
それでは，正五角形の内角の和は何度でしたか。
生徒Ａ：正五角形の内角の和は 度です。
先 生：そうですね。
生徒Ｂ：先生，私は大きさや形の異なる二等辺三角形がたくさん
あることに気づきました。
先 生：いろいろな図形がありますね。
他の図形を見つけた人はいませんか。
生徒Ｃ：はい。➀ひし形や台形もあると思います。
先 生：たくさんの図形を見つけましたね。
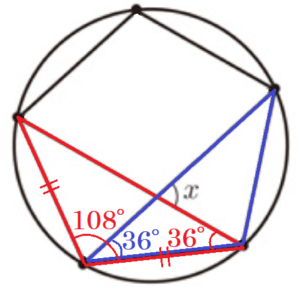
図形に注目すると，➁図の \( ∠x \) の大きさもいろいろな方法で
求めることができそうですね。
(1) にあてはまる数を書け。
右の図のように対角線をひくと，五角形は三角形を３つくっつけたものと考えることができます。
三角形の内角の和は \( 180° \) なので，五角形の内角の和は，
\( 180° \times 3=540° \)
(2) 下線部 ➀ について，ひし形の定義を下のア～エの中から1つ選び，記号で答えよ。
ア ４つの角がすべて等しい四角形
イ ４つの辺がすべて等しい四角形
ウ ２組の対辺がそれぞれ平行である四角形
エ 対角線が垂直に交わる四角形
(3) 下線部 ➁ について，\( ∠x \) の大きさを求めよ。
正五角形は，５つの内角がすべて等しく，内角の和は \( 540° \) なので，
１つの内角は，\( 540° \div 5=108° \)
また，正五角形は，すべての辺の長さが等しいので，
右の図の赤の三角形は二等辺三角形になっています。
ここから，底角は，\( \dfrac{180°-108°}{2}=36° \)
青の三角形は赤の三角形と合同になるので，底角は \( 36° \) になります。
ここで，\( ∠x \) は赤と青の三角形が重なっている
小さい三角形の外角になっているので，\( ∠x=36°+36°=72° \)
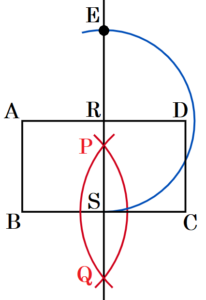
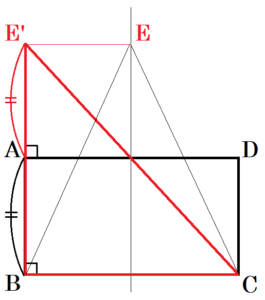
２ 右の図のような長方形 \( ABCD \) がある。次の【条件】を
すべて満たす点 \( E \) を，定規とコンパスを用いて作図せよ。
ただし，点 \( E \) の位置を示す文字 \( E \) を書き入れ，作図に用
いた線も残しておくこと。
【条件】
・ 線分 \( BE \) と線分 \( CE \) の長さは等しい。
・ \( △BCE \) と長方形 \( ABCD \) の面積は等しい。
・ 線分 \( AE \) の長さは，線分 \( BE \) の長さより短い。
手順１ 点 \( A，B \) を中心に円弧を描く。
（交点を点 \( P，Q \) とします）
手順２ ２点 \( P，Q \) を通る直線を描く。
（線分 \( AD，BC \) との交点を点 \( R，S \) とします）
手順３ 点 \( R \) を中心に線分 \( RS \) を半径とする円弧を描く。
手順３の円弧と手順２の直線の交点が求める点 \( E \) になります。
条件１より，点 \( E \) は線分 \( BC \) の垂直二等分線上にある点であるとわかります。
条件２より，線分 \( BC \) を固定して \( △BCE \) を等積変形し，
点 \( E \) が線分 \( AB \) の延長線上にある点を点 \( E’ \) とすると，
\( △BCE’ \) の面積は，\( BC \times BE’ \times \dfrac{1}{2} \)
長方形 \( ABCD \) の面積は，\( BC \times AB \)
と表すことができるので，
\( BC \times BE’ \times \dfrac{1}{2}=BC \times AB \)
\( BE’=2AB \)
となります。
条件３より，点 \( E \) は線分 \( BC \) よりも上側にあることがわかります。
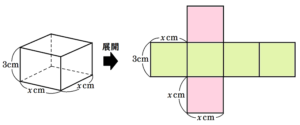
３ 底面が正方形で，高さが \( 3 \; cm \) の直方体がある。この直方体の表面積が \( 80 \; cm^2 \) であるとき，底面の正方形の一辺の長さを求めよ。ただし，底面の正方形の一辺の長さを \( x \; cm \) として，\( x \) についての方程式と計算過程も書くこと。
大問３
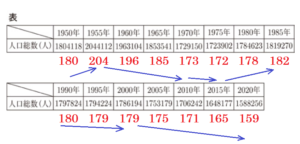
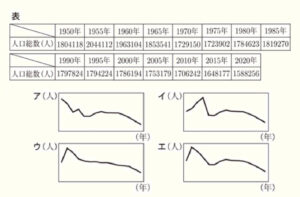
国勢調査(１９５０年～２０２０年)の結果をもとに表や図を作成した。次の１～３の問いに答えなさい。
１ 表は，鹿児島県の人口総数を表したものである。表をもとに，横軸を年，縦軸を人口総数として，その推移を折れ線グラフに表したとき，折れ線グラフの形として最も適当なものを下のア～エの中から１つ選び，記号で答えよ。
例）１９８５年の場合 ･･･ １８１９２７０ → １８２００００ → １８２
また，数値の上下変化を大まかに矢印で表してみます。
この矢印の形と最も近いのは エ になります。
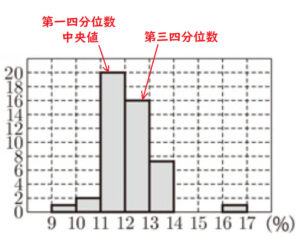
２ 図１は，２０２０年における都道府県別の人口に占める１５歳未満の人口の割合を階級の幅を１％にして，ヒストグラムに表したものである。鹿児島県は約１３．３％であった。次の (1)，(2) の問いに答えよ。
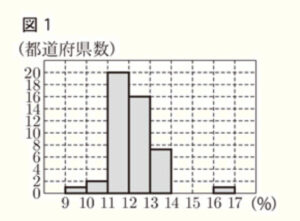
(1) 鹿児島県が含まれる階級の階級値を求めよ。
(2) ２０２０年における都道府県別の人口に占める１５歳未満の人口の割合を箱ひげ図に表したものとして，最も適当なものを下のア～エの中から１つ選び，記号で答えよ。
第三四分位数は，多い方から１２番目の値になります。
図１のヒストグラムから，
第一四分位数が含まれる階級は１１％以上１２％未満，
第三四分位数が含まれる階級は１２％以上１３％未満なので，
これを満たしている箱ひげ図は イ になります。
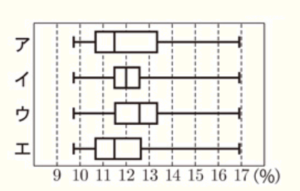
３ １９６０年から２０２０年まで１０年ごとの鹿児島県の市町村別の人口に占める割合について，図２は１５歳未満の人口の割合を，図３は６５歳以上の人口の割合を箱ひげ図に表したものである。
ただし，データについては，現在の４３市町村のデータに組み替えたものである。
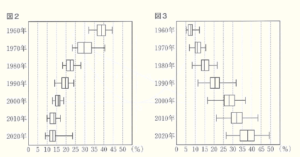
図２や図３から読みとれることとして，次の ➀～➄ は，「正しい」，「正しくない」，「図２や図３からはわからない」のどれか。最も適当なものを下のア～ウの中からそれぞれ１つ選び，記号で答えよ。
➀ 図２において，範囲が最も小さいのは１９９０年である。
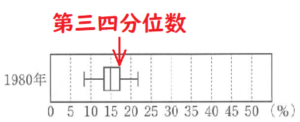
➁ 図３において，１９８０年の第３四分位数は１５％よりも大きい。
➂ 図２において，１５％を超えている市町村の数は，２０１０年よりも２０２０年の方が多い。
➃ 図３において，２０００年は３０以上の市町村が２５%を超えている。
➄ 図２の１９９０年の平均値よりも，図３の１９９０年の平均値の方が大きい。
ア 正しい イ 正しくない ウ 図２や図３からはわからない
１９９０年は約１０％，２０００年が約５％なので，正しくない。
➁
➂ ２０１０年，２０２０年ともに第三四分位数は１５％より小さくなっています。
市町村数は４３なので，第三四分位数が表すのは多い方から１１番目の値になります。
ここから，１５％を超えている市町村の数が１０未満であることはわかりますが，
それ以上絞り込むことはできません。
よって，図２からはわからないということになります。
➃ 第一四分位数が２５％を超えていて，少ない方から１１番目の値を表しているので，
３３以上の市町村が２５%を超えています。
➄ 箱ひげ図だけでは平均値を求めることはできません。
大問４
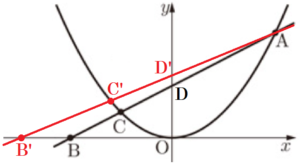
右の図で，放物線は関数 \( y=\dfrac{1}{4}x^2 \) のグラフであり，点 \( O \) は原点である。点 \( A \) は放物線上の点で，その \( x \) 座標は \( 4 \) である。点 \( B \) は \( x \) 軸上を動く点で，その \( x \) 座標は負の数である。２点 \( A，B \) を通る直線と放物線との交点のうち，\( A \) と異なる点を \( C \) とする。次の１～３の問いに答えなさい。
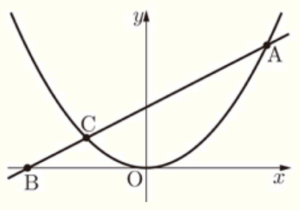
１ 点 \( A \) の \( y \) 座標を求めよ。
２ 点 \( B \) の \( x \) 座標が小さくなると，それにともなって小さくなるものを下のア～エの中からすべて選び，記号で答えよ。
ア 直線 \( AB \) の傾き イ 直線 \( AB \) の切片 ウ 点 \( C \) の \( x \) 座標 エ \( △OAC \) の面積
直線 \( AB \) の切片を \( D \) としています。
グラフから，
ア 直線 \( AB \) の傾き は小さくなっている
イ 直線 \( AB \) の切片 は大きくなっている
ウ 点 \( C \) の \( x \) 座標 は小さくなっている
とわかります。
エ \( △OAC \) の面積
\( △OAC=△OAD+△OCD \)，
\( △OAC’=△OAD’+△OC’D’ \)
となっています。
ここで，
\( △OAD<△OAD’，△OCD<△OC’D’ \)
なので，\( △OAC<△OAC’ \) となります。
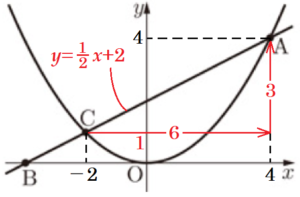
３ 点 \( C \) の \( x \) 座標が \( -2 \) であるとき，次の (1)，(2) の問いに答えよ。
(1) 点 \( B \) の座標を求めよ。ただし，求め方や計算過程も書くこと。
\( y=\dfrac{1}{4}x^2 \) に \( x=-2 \) を代入すると，
\( y=\dfrac{1}{4} \times 2^2=1 \)
よって，点 \( C \) の座標は，\( (-2，1) \)
直線 \( AC \) の傾きは，\( \dfrac{4-1}{4-(-2)}=\dfrac{1}{2} \)
直線 \( AC \) の式を \( y=\dfrac{1}{2}x+b \) とすると，
\( (-2，1) \) を通るので，
\( 1=\dfrac{1}{2} \times (-2)+b \)
\( b=2 \)
よって，直線 \( AC \) の式は，\( y=\dfrac{1}{2}x+2 \)
点 \( B \) は，\( y=\dfrac{1}{2}x+2 \) 上の点で， \( y \) 座標が \( 0 \) なので，
\( 0=\dfrac{1}{2}x+2 \)
\( \dfrac{1}{2}x=-2 \)
\( x=-4 \)
以上より，点 \( B \) の座標は，\( (-4，0) \)
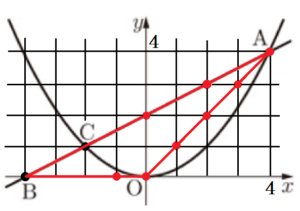
(2) 大小２個のさいころを同時に投げ，大きいさいころの出た目の数を \( a \)，小さいさいころの出た目の数を \( b \) とするとき，座標が \( (a-2，b-1) \) である点を \( P \) とする。点 \( P \) が３点 \( O，A，B \) を頂点とする \( △OAB \) の辺上にある確率を求めよ。ただし，大小２個のさいころはともに，１から６までのどの目が出ることも同様に確からしいものとする。
また，\( a，b \) は自然数なので，\( a-2，b-1 \) は整数になります。
\( -1≦a-2≦4，0≦b-1≦5 \) を満たす座標のうち，\( x \) 座標，\( y \) 座標がともに整数になるのは，
\( (a-2，b-1)=(-1，0)，(0，0)，(0，2)，(1，1)，(2，2)，(2，3)，(3，3)，(4，4) \) の８個。
取り得る座標は全部で３６個あるので，求める確率は，\( \dfrac{8}{36}=\dfrac{2}{9} \)
大問５
図１のような \( AB=6 \; cm，BC=3 \; cm \) である長方形 \( ABCD \) がある。
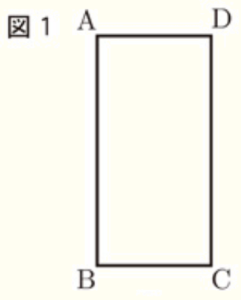
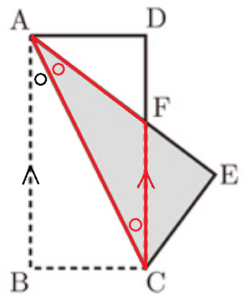
図２は，図１の長方形 \( ABCD \) を対角線 \( AC \) を折り目として折り返したとき，点 \( B \) の移った点を \( E \) とし，線分 \( AE \) と辺 \( DC \) の交点を \( F \) としたものである。
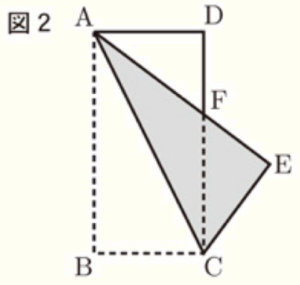
図３は，図２の折り返した部分をもとに戻し，長方形 \( ABCD \) を対角線 \( DB \) を折り目として折り返したとき，点 \( C \) の移った点を \( G \) とし，線分 \( DG \) と辺 \( AB \) の交点を \( H \) としたものである。
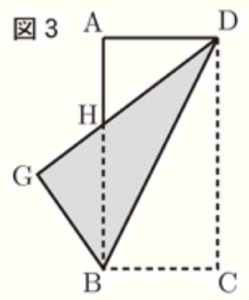
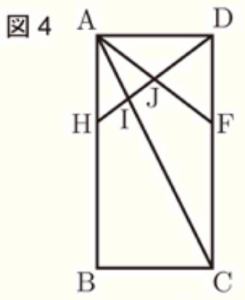
図４は，図３の折り返した部分をもとに戻し，線分 \( DH \) と対角線 \( AC \)，線分 \( AF \) の交点をそれぞれ \( I，J \) としたものである。
次の１～４の問いに答えなさい。
１ 長方形 \( ABCD \) の対角線 \( AC \) の長さを求めよ。
２ 図２において，\( △ACF \) が二等辺三角形であることを証明せよ。
\( △ACF \) において，
長方形の向かい合う辺は平行なので，錯角は等しく，
\( ∠FCA=∠BAC \) ･･･ ➀
折り返す前後の図形は合同なので，
\( ∠FAC=∠BAC \) ･･･ ➁
➀➁より，\( ∠FCA=∠FAC \)
よって，底角が等しいので，\( △ACF \) は二等辺三角形である。
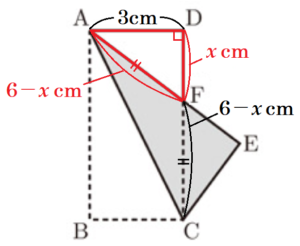
３ 線分 \( DF \) の長さを求めよ。
\( DF=x \; cm \) とすると，
\( CF=6-x \; cm \) と表すことができます。
問２より，\( △ACF \) は \( AF=CF \) の二等辺三角形なので，
\( AF=CF=6-x \; cm \)
\( △ADF \) において，三平方の定理より，
\( x^2+3^2=(6-x)^2 \)
\( x^2+9=x^2-12x+36 \)
\( 12x=27 \)
\( x=\dfrac{9}{4} \; (cm) \)
４ \( △AIJ \) の面積を求めよ。
この問題では，\( AD//HF \) であることに気付くことができれば，\( △ADJ≡△FHJ \)，\( △ADI \) ∽ \( △KHI \) であることを使って，線分 \( HI，IJ，DJ \) の比を求めることができます。
（線分 \( AC \) と線分 \( HF \) の交点を点 \( K \) としています。）
図２と図３ は折り返し方を左右入れ替えただけなので，\( AH=DF \)
\( AH//DF，AH=DF \) より，四角形 \( AHFD \) は長方形になります。
このとき，線分 \( AF，DH \) は対角線になっているので，
\( △ADJ≡△FHJ \) となります。
よって，\( HJ：DJ=1：1 \) ･･･ ➀
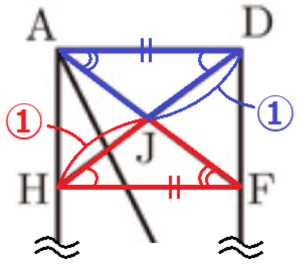
注）図の上半分のみ記載しています
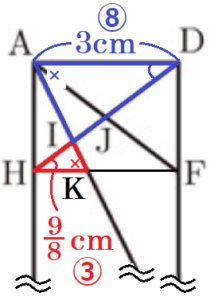
次に，線分 \( AC \) と線分 \( HF \) の交点を点 \( K \) とすると，
\( △AHK \) ∽ \( △ABC \) なので，
\( AH=DF=\dfrac{9}{4} \; cm，AB=6 \; cm，BC=3 \; cm \) より，
\( HK：BC=AH：AB \)
\( HK：3=\dfrac{9}{4}：6 \)
\( 6HK=\dfrac{27}{4} \)
\( HK=\dfrac{9}{8} \; (cm) \)
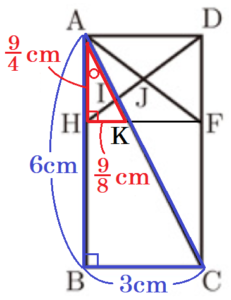
\( △KHI \) ∽ \( △ADI \) なので，
\( HK=\dfrac{9}{8} \; cm，AD=3 \; cm \) より，
\( HI：DI=HK：AD=\dfrac{9}{8}：3=3：8 \) ･･･ ➁
注）図の上半分のみ記載しています
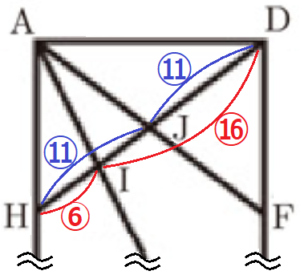
➀より，\( HJ：DJ=1：1=11：11 \)
➁より，\( HI：DI=3：8=6：16 \)
ここから，
\( HI：IJ：DJ=HI：(DI-DJ)：DJ \)
\( =6：(16-11)：11 \)
\( =6：5：11 \)
よって，\( IJ：DH=5：22 \)
注）図の上半分のみ記載しています
\( △ADH \) と \( △AIJ \) は高さが等しいので，底辺の長さの比が面積比と等しくなります。
よって，
\( △AIJ：△ADH=IJ：DH=5：22 \)
\( 22△AIJ=5△ADH \)
\( △AIJ=\dfrac{5}{22}△ADH \)
\( AD=3 \; cm，AH=\dfrac{9}{4} \; cm \) より，\( △ADH=3 \times \dfrac{9}{4} \times \dfrac{1}{2}=\dfrac{27}{8} \; (cm^2) \) なので，
\( △AIJ=\dfrac{5}{22} \times \dfrac{27}{8}=\dfrac{135}{176} \; (cm^2) \)
