大問１
１ \( -9+2 \) を計算しなさい。
２ \( -15 \div \left( -\dfrac{5}{3} \right) \) を計算しなさい。
３ \( 110 \) を素因数分解しなさい。
４ 等式 \( 4a-9b+3=0 \) を \( a \) について解きなさい。
５ 連立方程式 \( \left\{ \begin{array}{}
3x-y=17 \\
2x-3y=30 \\
\end{array} \right. \) を解きなさい。
６ \( \sqrt{54}+\dfrac{12}{\sqrt{6}} \) を計算しなさい。
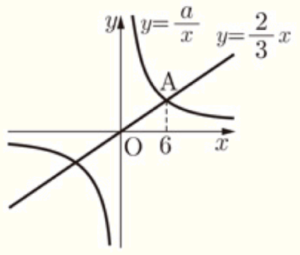
７ 下の図のように，比例 \( y=\dfrac{2}{3}x \) のグラフと反比例 \( y=\dfrac{a}{x} \) のグラフとの交点のうち，\( x \) 座標が正である点を \( A \) とします。点 \( A \) の \( x \) 座標が \( 6 \) のとき，\( a \) の値を求めなさい。
８ ある学年のＡ組，Ｂ組，Ｃ組は，どの組にも３５人の生徒が在籍しています。これら３つの組の各生徒を対象に，１か月間に図書室から借りた本の冊数を調べました。下の図は，組ごとに，各生徒が借りた本の冊数の分布のようすを箱ひげ図に表したものです。この箱ひげ図から必ずいえることを，あとのア～エから1つ選び，記号で答えなさい。
ア 第１四分位数は，Ａ組とＢ組で同じである。
イ 四分位範囲がもっとも小さいのは，Ａ組である。
ウ 借りた本の冊数が６冊以上である人数は，Ｂ組がもっとも多い。
エ 借りた本の冊数が２冊以上８冊以下である人数は，Ｃ組がもっとも多い。
大問２
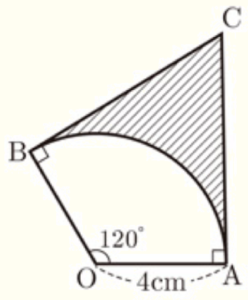
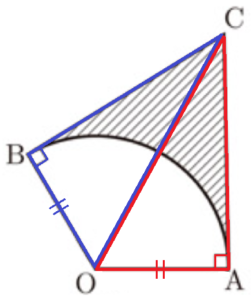
１ 右の図のような，半径が \( 4 \; cm \) ，中心角が \( 120° \) のおうぎ形 \( OAB \) があります。点 \( A \) を通って線分 \( OA \) に垂直な直線と，点 \( B \) を通って線分 \( OB \) に垂直な直線をひき，その交点を \( C \) とします。
次の (1)，(2) の問いに答えなさい。ただし，円周率を \( \pi{} \) とします。
(1) 弧 \( AB \) の長さを求めなさい。
(2) 弧 \( AB \) と線分 \( AC \)，線分 \( BC \) とで囲まれた斜線部分の面積を求めなさい。
円の半径と２本の接線で囲まれる四角形を，２接線の交点と円の中心を通る直線で分けてできる２つの三角形は合同になります。
（詳細は別途解説します）
\( △AOC≡△BOC，∠AOB=120° \) より，
\( ∠AOC=60° \) なので，
\( AC=\sqrt{3}OA=4\sqrt{3} \; (cm) \)
四角形 \( OACB=2 \times OA \times AC \times \dfrac{1}{2} \)
\( =2 \times 4 \times 4\sqrt{3} \times \dfrac{1}{2} \)
\( =16\sqrt{3} \; (cm^2) \)
おうぎ形 \( OAB=\pi{} \times OA^2 \times \dfrac{∠AOB}{360°} \)
\( =\pi{} \times 4^2 \times \dfrac{120°}{360°} \)
\( =\dfrac{16}{3}\pi{} \; (cm^2) \)
よって，
斜線部分の面積 \( =16\sqrt{3}-\dfrac{16}{3}\pi{} \; (cm^2) \)
円の半径と接線は接点において垂直に交わるので，
\( OA⊥AC，OB⊥BC \) であり，
\( △OAC，△OBC \) は直角三角形になります。
\( △OAC \) と \( △OBC \) において，
円 \( O \) の半径なので，\( OA=OB \) ･･･ ➀
\( OC \) は共通 ･･･ ➁
➀➁より，
直角三角形において，斜辺と他の１辺がそれぞれ等しいので，
\( △OAC≡△OBC \)
２ 哲也さんと舞さんは，坂の途中にある \( A \) 地点からボールを転がしたときの，ボールの転がる時間と距離の関係を調べました。その結果，ボールが転がり始めてから \( x \) 秒間に転がる距離を \( y \; m \) としたとき，\( x \) と \( y \) の関係は，\( y=\dfrac{1}{4}x^2 \) であることがわかりました。右の図は，そのときの \( x \) と \( y \) の関係を表したグラフです。
次の (1)，(2) の問いに答えなさい。
(1) 関数 \( y=\dfrac{1}{4}x^2 \) について，\( x \) の値が \( 0 \) から \( 6 \) まで増加するときの変化の割合を求めなさい。
(2) 舞さんは，一定の速さで坂を下っています。舞さんが \( A \) 地点を通過するのと同時に，哲也さんは，\( A \) 地点からボールを転がしました。ボールが転がり始めてから \( 6 \) 秒後にボールは舞さんに追いつき，ボールが舞さんを追いこしてからは，舞さんとボールの間の距離はしだいに大きくなりました。
ボールが舞さんを追いこしてから，舞さんとボールの間の距離が \( 18 \; m \) になったのは，ボールが転がり始めてから何秒後ですか。
３ 赤球と白球がたくさん入っている箱の中に，赤球が何個あるかを推定します。最初に箱の中にあった赤球と白球の個数の比は \( 4：1 \) であったことがわかっています。この箱に白球を３００個追加し，箱の中の球をよくかき混ぜました。そのあと，１２０個の球を無作為に抽出したところ，赤球が８０個ありました。
この結果から，最初に箱の中にあった赤球は，およそ何個と考えられますか。
４ 下の図のように，１００行３列のマス目がある表に，次の【規則】にしたがって，１から３００までの自然数が１から順に，１つのマスに１つずつ入っています。ただし，表の中の・は，マスに入る自然数を省略して表したものです。
➀ １行目は，１列目に１，２列目に２，３列目に３を入れる。
➁ ２行目以降は，１つ前の行に入れたもっとも大きい自然数より
１大きい数から順に，次のとおり入れる。
偶数行目は，３列目，２列目，１列目の順で数を入れる。
奇数行目は，１列目，２列目，３列目の順で数を入れる。
たとえば，８は，３行目の２列目のマスに入っています。
次の (1)，(2) の問いに答えなさい。
(1) ４５は，何行目の何列目のマスに入っていますか。
(2) \( n \) 行目のマスに入っている３つの自然数のうち，もっとも小さいものを \( P \) とします。
次の (ア)，(イ) の問いに答えなさい。ただし，\( n \) は１以上１００以下とします。
(ア) 自然数 \( P \) を \( n \) を使った式で表しなさい。
(イ) \( n \) が２以上のとき，\( n \) 行目の１つ前の行を \( (n-1) \) 行目とします。\( (n-1) \) 行目のマスに入っている３つの自然数のうち，もっとも大きいものを \( Q \) とします。\( P+Q=349 \) のとき，\( n \) 行目の３列目のマスに入っている自然数を求めなさい。
大問３
数学の授業で，生徒たちが，直線 \( y=x \) と三角形を素材にした応用問題を考えることになりました。
次の１，２の問いに答えなさい。
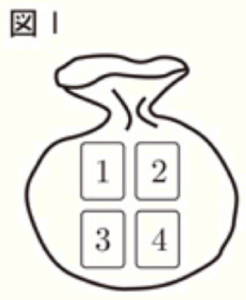
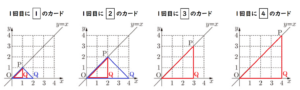
１ 京子さんと和真さんは，確率を求める問題をつくろうとしています。２人は，図Ⅰのような， \( 1，2，3，4 \) の数字が１つずつ書かれた４枚のカードが入った袋を使い，次の【操作】をすることを考え，それをもとに会話をしています。
あとの(1) ，(2)の問いに答えなさい。
・袋の中のカードをよくかき混ぜて，カードを１枚取り出し，
カードに書かれた数を確認してからもとにもどす。この作業を
２回行う。
・１回目に取り出したカードに書かれた数を \( a \) として，
直線 \( y=x \) 上に \( (a，a) \) となる点 \( P \) をとる。
・２回目に取り出したカードに書かれた数を \( b \) として，
\( x \) 軸上に \( (b，0) \) となる点 \( Q \) をとる。
・原点 \( O \)，点 \( P \)，点 \( Q \) をそれぞれ結んで \( △OPQ \) をつくる。
京子さん：この【操作】をすると，取り出すカードによって，
さまざまな形の \( △OPQ \) ができるね。
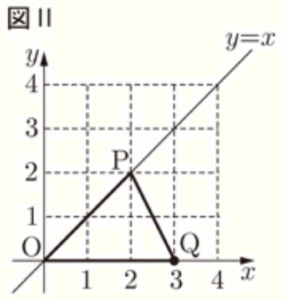
和真さん：たとえば，取り出したカードに書かれた数が，
１回目が \( 2 \) で，２回目が \( 3 \) のときの \( △OPQ \) は
図Ⅱのようになるよ。他の場合もやってみよう。
京子さん：すべての場合をかいたけれど，この中に，合同な
三角形の組はないようだね。つまり，【操作】に
したがって \( △OPQ \) をつくるとき，\( △OPQ \) は
全部で ① 通りあるね。
和真さん：\( △OPQ \) が直角三角形になる場合があったよ。
この確率を求める問題にしよう。
(1) ① にあてはまる正しい数を答えなさい。
(2) 【操作】にしたがって \( △OPQ \) をつくるとき，\( △OPQ \) が直角三角形になる確率を求めなさい。
必ず，直角二等辺三角形になります。
１回目にひいたカードを１から４まで順番に固定して，
２回目にどのカードをひいたら \( △OPQ \) が直角二等辺三角形になるのかをグラフから考えると，
全部で次の６通りがあります。
よって，求める確率は，\( \dfrac{6}{16}=\dfrac{3}{8} \)
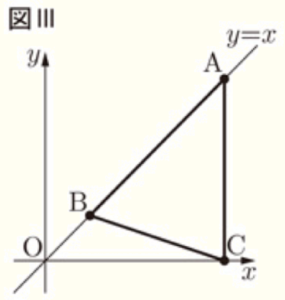
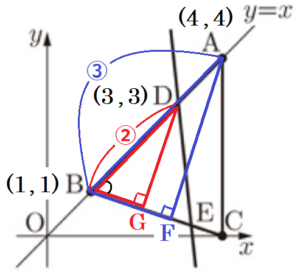
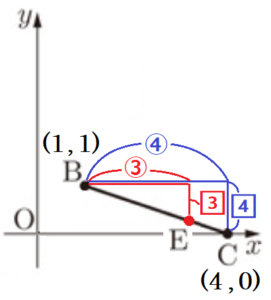
２ 優矢さんと志保さんは，三角形の面積を２等分する問題をつくろうとしています。２人は，直線 \( y=x \) 上の２点 \( (4，4)，(1，1) \) をそれぞれ \( A，B，x \) 軸上の点 \( (4，0) \) を \( C \) とし，３点 \( A，B，C \) をそれぞれ結んで，\( △ABC \) をつくりました。図Ⅲは，直線 \( y=x \) と \( △ABC \) をかいたものです。２人は，図Ⅲを見ながら，次の会話をしています。
あとの (1)～(3) の問いに答えなさい。
優矢さん：頂点 \( A \) を通り，\( △ABC \) の面積を２等分する直線は，
\( △ABC \) が二等辺三角形ではないようだから，
➁ だね。
志保さん：頂点を通らない直線で \( △ABC \) の面積を２等分する
場合も考えてみようよ。
優矢さん：直線 \( y=x \) 上の点 \( (3，3) \) を \( D \) として，点 \( D \) を通り，
\( △ABC \) の面積を２等分する直線だとどうなるかな。
志保さん：その直線は辺 \( BC \) と交わりそうだよ。その直線と辺 \( BC \)
との交点の座標を求める問題にしよう。
(1) ➁ にあてはまるものとして正しいものを，次のア～エから１つ選び，記号で答えなさい。
ア \( ∠BAC \) の二等分線
イ 辺 \( BC \) の垂直二等分線
ウ 頂点 \( A \) から辺 \( BC \) への垂線
エ 頂点 \( A \) と辺 \( BC \) の中点を通る直線
(2) ２点 \( B，C \) を通る直線の式を求めなさい。
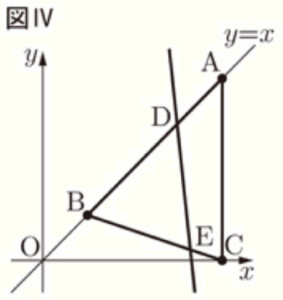
(3) 図Ⅳは，優矢さんと志保さんが，図Ⅲにおいて，点 \( D \) を通り，\( △ABC \) の面積を２等分する直線をかき，その直線と辺 \( BC \) との交点を \( E \) としたものです。点 \( E \) の座標を求めなさい。
点 \( A，D \) から辺 \( BC \) に垂線をひき，交点を点 \( F，G \) とすると，
\( ∠B \) は共通，\( ∠DGB=∠AFB=90° \) より，
２組の角がそれぞれ等しいので，\( △DBG \) ∽ \( △ABF \) であり，
相似比は，\( DB：AB=2：3 \)
よって，\( DG：AF=2：3 \) であり，\( DG=\dfrac{2}{3}AF \)
このとき，線分 \( DG，AF \) は，
それぞれ \( △DBE，△ABC \) の高さになっています。
\( △DBE=BE \times DG \times \dfrac{1}{2} \)
\( =BE \times \dfrac{2}{3}AF \times \dfrac{1}{2} \)
\( △ABC=BC \times AF \times \dfrac{1}{2} \)
なので，
\( △DBE：△ABC=\left( BE \times \dfrac{2}{3}AF \times \dfrac{1}{2} \right)：\left( BC \times AF \times \dfrac{1}{2} \right) \)
\( =\dfrac{2}{3}BE：BC \)
\( =2BE：3BC \)
\( △DBE：△ABC=1：2 \) のとき，
\( △DBE：△ABC=1：2 \)
\( 2BE：3BC=1：2 \)
\( 4BE=3BC \)
\( BE=\dfrac{3}{4}BC \)
\( B(1，1)，C(4，0) \) なので，\( BE=\dfrac{3}{4}BC \) のとき，
点 \( E \) の \( x \) 座標は，
点 \( B \) の \( x \) 座標より \( 3 \times \dfrac{3}{4}=\dfrac{9}{4} \) 大きい値であり，
\( 1+\dfrac{9}{4}=\dfrac{13}{4} \)
点 \( E \) の \( y \) 座標は，
点 \( B \) の \( y \) 座標より \( 1 \times \dfrac{3}{4}=\dfrac{3}{4} \) 小さい値であり，
\( 1-\dfrac{3}{4}=\dfrac{1}{4} \)
になります。
よって，\( E \left( \dfrac{13}{4}，\dfrac{1}{4} \right) \)
大問４
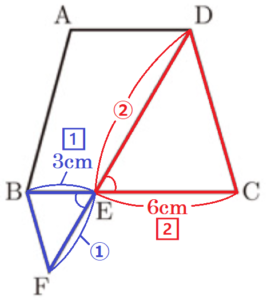
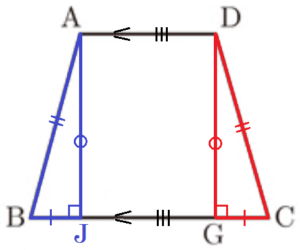
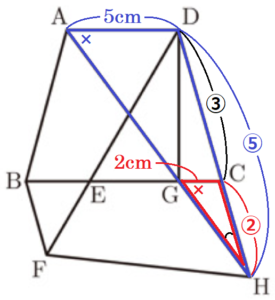
図Ⅰのような，\( AB=DC=7 \; cm，AD=5 \; cm，BC=9 \; cm \)，\( AD//BC \) の台形 \( ABCD \) があります。辺 \( BC \) 上に，\( BE=3 \; cm \) となる点 \( E \) をとります。また，直線 \( DE \) 上に，\( DE：EF=2：1 \) となる点 \( F \) を，直線 \( BC \) に対して点 \( D \) と反対側にとり，点 \( B \) と点 \( F \) を結びます。
次の１～３の問いに答えなさい。
１ \( △CDE \) ∽ \( △BFE \) であることを証明しなさい。
\( △CDE \) と \( △BFE \) において，
仮定より，
\( CE：BE=(BC-BE)：BE=(9-3)：3=2：1 \) ･･･ ➀
\( DE：EF=2：1 \) ･･･ ➁
対頂角は等しいので，
\( ∠CED=∠BEF \) ･･･ ➂
➀➁➂より，２組の辺の比とその間の角がそれぞれ等しいので，
\( △CDE \) ∽ \( △BFE \)
２ 線分 \( BF \) の長さを求めなさい。
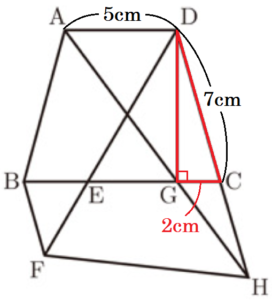
３ 図Ⅱは，図Ⅰにおいて，点 \( D \) から辺 \( BC \) に垂線をひき，辺 \( BC \) との交点を \( G \) としたものです。また，直線 \( AG \) と直線 \( DC \) との交点を \( H \) とし，点 \( F \) と点 \( H \) を結びます。
次の (1)，(2) の問いに答えなさい。
(1) 線分 \( DG \) の長さを求めなさい。
台形 \( ABCD \) は等脚台形なので，
\( CG=\dfrac{BC-AD}{2}=\dfrac{9-5}{2}=2 \; (cm) \)
\( △CDG \) において，三平方の定理より，
\( DG^2=7^2-2^2=45 \)
\( DG=3\sqrt{5} \; (cm) \) (\( DG>0 \)より)
点 \( A \) から線分 \( BC \) に垂線をひき，交点を点 \( J \) とします。
\( △CDG \) と \( △BAJ \) において，
仮定より，
\( AB=DC \) ･･･ ➀
\( DG⊥BC \) ･･･ ➁
\( AJ⊥BC \) ･･･ ➂
➁➂より，\( ∠DGC=∠AJB=90° \) ･･･ ➃
\( AD//BC，DG⊥BC，AJ⊥BC \) より，四角形 \( AJGD \) は長方形なので，
\( DG=AJ \) ･･･ ➄
➀④➄より，
直角三角形において，斜辺と他の１辺がそれぞれ等しいので，
\( △CDG≡△BAJ \)
対応する辺の長さは等しいので，\( CG=BJ \)
よって，
\( BC=BJ+GJ+CG=2CG+AD \)
\( 2CG=BC-AD \)
\( CG=\dfrac{BC-AD}{2} \)
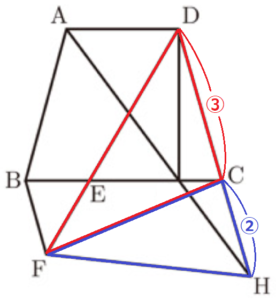
(2) 四角形 \( BFHC \) の面積を求めなさい。
四角形 \( BFHC=△BCF+△FCH \) として求めます。
【\( △BCF \) の面積】
点 \( F \) から線分 \( BC \) に垂線をひき，
交点を点 \( K \) とします。
\( △CDE \) ∽ \( △BFE \) で，相似比は \( 2：1 \) なので，
\( DG：FK=2：1 \)
\( 3\sqrt{5}：FK=2：1 \)
\( FK=\dfrac{3\sqrt{5}}{2} \; (cm) \)
よって，
\( △BCF=BC \times FK \times \dfrac{1}{2} \)
\( =9 \times \dfrac{3\sqrt{5}}{2} \times \dfrac{1}{2} \)
\( =\dfrac{27\sqrt{5}}{4} \; (cm^2) \)
【\( △FCH \) の面積】
相似な三角形の対応する角は等しいので，\( ∠EBF=∠ECD \) で，
錯角が等しく，\( BF//CD \)
等積変形の考え方から，\( △BCD=△FCD \) なので，
\( △FCD=△BCD=BC \times DG \times \dfrac{1}{2} \)
\( =9 \times 3\sqrt{5} \times \dfrac{1}{2} \)
\( =\dfrac{27\sqrt{5}}{2} \; (cm^2) \)
\( △HGC \) と \( △HAD \) において，
\( AD//BC \) より，\( ∠HGC=∠HAD \)
\( ∠H \) は共通
なので，\( △HGC \) ∽ \( △HAD \) であり，
相似比は，\( GC：AD=2：5 \)
よって，\( HC：HD=2：5 \) なので，
\( HC：CD=HC：(HD-HC)=2：(5-2)=2：3 \)
\( =2：(5-2) \)
\( =2：3 \)
\( △FCD \) と \( △FCH \) の底辺をそれぞれ \( CD，HC \) とすると，
高さが共通であり，底辺の比が面積比になるので，
\( △FCD：△FCH=HC：CD \)
\( \dfrac{27\sqrt{5}}{2}：△FCH=3：2 \)
\( △FCH=9\sqrt{5} \; (cm^2) \)
以上より，
四角形 \( BFHC=△BCF+△FCH \)
\( =\dfrac{27\sqrt{5}}{4}+9\sqrt{5} \)
\( =\dfrac{63\sqrt{5}}{4} \; (cm^2) \)
