大問1
(1) 次の計算をしなさい。
➀ \( (-21) \div 7 \)
➁ \( -\dfrac{3}{4}+\dfrac{5}{6} \)
【解説】
\( =\dfrac{-3 \times 3+5 \times 2}{12} \)
\( =\dfrac{1}{12} \)
➂ \( (-3a) \times (-2b)^3 \)
【解説】
\( =-3a \times (-8b^3) \)
\( =24ab^3 \)
➃ \( \sqrt{8}-\sqrt{18} \)
【解説】
\( =2\sqrt{2}-3\sqrt{2} \)
\( =-\sqrt{2} \)
(2) ある球の半径を2倍にすると,体積はもとの球の体積の何倍になるか,求めなさい。
【解説】
もとの球の半径を \( r \) とすると,体積は \( \dfrac{4}{3}\pi{}r^3 \) と表すことができます。
ここで,半径を2倍 \( 2r \) にすると,体積は
\( \dfrac{4}{3}\pi{} \times (2r)^3=\dfrac{4}{3}\pi{} \times 8r^3 \)
\( =8 \times \dfrac{4}{3}\pi{}r^3 \)
と表すことができます。
よって,体積は8倍になります。
大問2
(1) 桃の果汁が \( 31 \; \% \) の割合で含まれている飲み物がある。この飲み物 \( a \; mL \) に含まれている桃の果汁の量は何 \( mL \) か,\( a \) を使った式で表しなさい。
【解答】
\( \dfrac{31}{100}a \; mL \)
(2) 等式 \( 3x+2y-4=0 \) を \( y \) について解きなさい。
【解答】
\( y=-\dfrac{3}{2}x+2 \)
【解説】
\( 3x+2y-4=0 \)
\( 2y=-3x+4 \)
\( y=-\dfrac{3}{2}x+2 \)
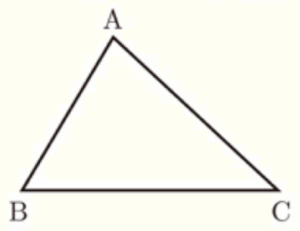
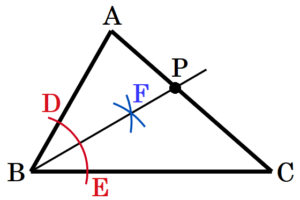
(3) 右の図のような,\( △ABC \) がある。
辺 \( AC \) 上にあって,辺 \( AB,BC \) までの距離が等しい点 \( P \) を,定規とコンパスを用いて作図によって求め,\( P \) の位置を示す文字 \( P \) も書きなさい。
ただし, 作図に用いた線は消さずに残しておきなさい。
【解答】
手順1 点 \( P \) を中心に円弧を描く。
(線分 \( AB,BC \) との交点を点 \( D,E \) とします。)
手順2 点 \( D,E \) を中心に円弧を描く。
(交点を点 \( F \) とします。)
手順3 2点 \( B,F \) を通る直線を描く。
手順3の直線と線分 \( AC \) の交点が,求める点 \( P \) になります。
【解説】
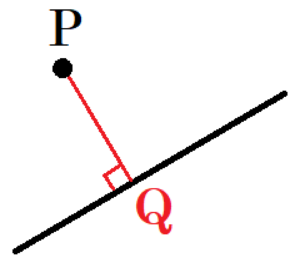
「点 \( P \) から線分までの距離」というのは,点 \( P \) から線分に垂線をひいたときの垂線の長さになります。
(右の図で線分 \( PQ \) の長さ)
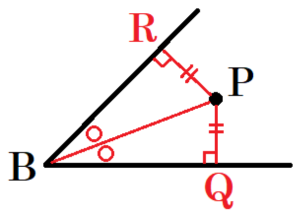
また,右の図のように点 \( P \) と二直線までの距離が等しいとき,
斜辺と他の1辺の長さが等しいので,\( △BPQ≡△BPR \) です。
合同な三角形の対応する角は等しいので,\( ∠PBQ=∠PBR \)
ここから,線分 \( BP \) は \( ∠B \) の二等分線になります。
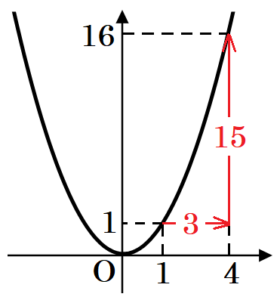
(4) 関数 \( y=x^2 \) について,\( x \) の値が \( 1 \) から \( 4 \) まで増加するときの変化の割合を求めなさい。
【解説】
変化の割合は \( \dfrac{y \; の増加量}{x \; の増加量} \;\;\;\; \) で求めることができます。
\( x=1 \) のとき,\( y \) の値は \( y=1^2=1 \)
\( x=4 \) のとき,\( y \) の値は \( y=4^2=16 \)
よって,
変化の割合 \( =\dfrac{16-1}{4-1}=5 \)
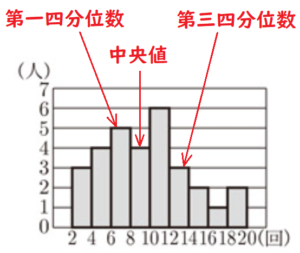
(5) 図1は,ある学級の生徒30人について,先月の図書館の利用回数を調べ,その分布のようすをヒストグラムに表したものである。例えば,利用回数が2回以上4回未満の生徒は3人であることがわかる。また,図2のア~エのいずれかは,この利用回数の分布のようすを箱ひげ図に表したものである。その箱ひげ図をア~エの中から1つ選び,記号で答えなさい。
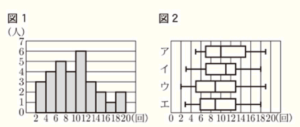
【解説】
学級の生徒30人が30人なので,
第一四分位数は少ない方から8番目の人の値,
中央値は15番目と16番目の人の値の平均値,
第三四分位数は多い方から8番目の人の値です。
図1のヒストグラムから
第一四分位数が含まれる階級は6回以上8回未満,
中央値が含まれる階級は8回以上10回未満,
第三四分位数が含まれる階級は12回以上14回未満
なので,
これらをすべて満たしている箱ひげ図は エ です。
大問3
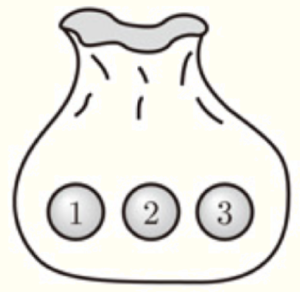
(1) 右の図のように,袋の中に \( 1,2,3 \) の数字が1つずつ書かれた3個の玉が入っている。A,Bの2人が,この袋の中から,<取り出し方のルール> の (ア) ,(イ) のいずれかにしたがって,1個ずつ玉を取り出し,書かれた数が大きいほうの玉を取り出した人が景品をもらえるゲームを考える。書かれた数が等しい場合には2人とも景品はもらえない。ただし,どの玉を取り出すことも同様に確からしいものとする。
<取り出し方のルール>
(ア) はじめにAが玉を取り出す。次に,その取り出した玉を袋の中にもどし,よくかき混ぜてからBが玉を取り出す。
(イ) はじめにAが玉を取り出す。次に,その取り出した玉を袋の中にもどさず,続けてBが玉を取り出す。
➀ ルール (ア) にしたがったとき,Aが景品をもらえる確率を求めなさい。
【解説】
AとBが取り出した玉の数字の組み合わせを樹形図で表し,Aが景品がもらえる場合に
○ をつけてみます。
Aが景品がもらえる組み合わせは3通り,すべての組み合わせは9通りなので,
確率は,\( \dfrac{3}{9}=\dfrac{1}{3} \)
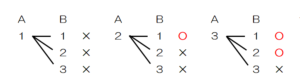
➁ Aが景品をもらえない確率が大きいのは,ルール (ア),(イ) のどちらのルールにしたがったときか。ア,イの記号で答え,その確率も書きなさい。
【解答】
ルール (ア) にしたがったとき
確率 ・・・ \( \dfrac{2}{3} \)
【解説】
【ルール (ア) の場合】
➀ より,Aが景品をもらえる確率は \( \dfrac{1}{3} \) なので,もらえない確率は,\( 1-\dfrac{1}{3}=\dfrac{2}{3} \)
【ルール (イ) の場合】
➀ の場合と同様に樹形図に表すと,
Aが景品がもらえない組み合わせは3通り,すべての組み合わせは6通りなので,
確率は,\( \dfrac{3}{6}=\dfrac{1}{2} \)

以上より,Aが景品をもらえない確率が大きいのは,ルール (ア) の場合になります。
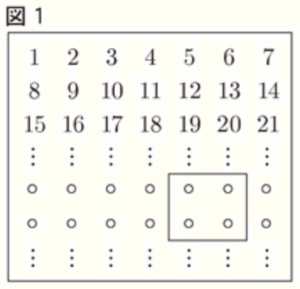
(2) 図1のように,整数を \( 1 \) から順に1段に7つずつ並べたものを考え,縦,横に2つずつ並んでいる4つの整数を四角形で囲む。ただし,◦は整数を省略したものであり,囲んだ位置は例である。
このとき,囲んだ4つの整数を
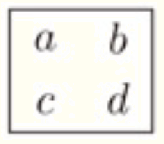
とすると, \( ad-bc \) はつねに同じ値になる。
➀ \( ad-bc \) の値を求めなさい。
【解説】
4つの数字 \( 1,2,8,9 \) を囲んだとすると,\( a=1,b=2,c=8,d=9 \) となるので,
\( ad-bc=1 \times 9-2 \times 8=-7 \)
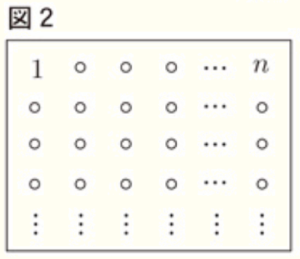
➁ 図2のように,1段に並べる整数の個数を \( n \) に変えたものを考える。ただし,\( n \) は \( 2 \) 以上の整数とする。
このとき,\( ad-bc \) はつねに \( n \) を使って表された同じ式になる。その式を解答用紙の( )の中に書きなさい。また,それがつねに成り立つ理由を説明しなさい。
【解答】
左上の数を \( a \) とすると,\( b,c,d \) はそれぞれ,
\( b=a+1,c=a+n,d=a+n+1 \) と表すことができます。
このとき,
\( ad-bc=a(a+n+1)-(a+1)(a+n) \)
\( =(a^2+an+a)-(a^2+an+a+n) \)
\( =-n \)
よって,\( a \) の値にかかわらず,\( ad-bc \) の値は \( -n \) で一定になります。
大問4
ある中学校で地域の清掃活動を行うために,生徒200人が4人1組または5人1組のグループに分かれた。ごみ袋を配るとき,1人1枚ずつに加え,グループごとの予備として4人のグループには2枚ずつ,5人のグループには3枚ずつ配ったところ,配ったごみ袋は全部で314枚であった。
このとき,4人のグループの数と5人のグループの数をそれぞれ求めなさい。求める過程も書きなさい。
【解答】
4人1組のグループ数を \( a \) 組,5人1組のグループ数を \( b \) 組とすると,
生徒数の関係を表す方程式は,
\( 4a+5b=200 \) ・・・ ➀
配ったごみ袋の枚数を表す方程式は,
\( 2a+3b+200=314 \) ・・・ ➁
これらを連立方程式として解くと,
\( \left\{ \begin{array}{}
4a+5b=200 ・・・ ➀ \\
2a+3b+200=314 ・・・ ➁ \\
\end{array} \right. \)
➁ より,
\( 2a+3b=114 \) ・・・ ➁’
➁’\( \times 2-\) ➀
\( b=28 \)
➀ に代入すると,
\( 4a+5 \times 28=200 \)
\( 4a+140=200 \)
\( 4a=60 \)
\( a=15 \)
よって,4人1組のグループ数は15組,5人1組のグループ数は28組になります。
大問5
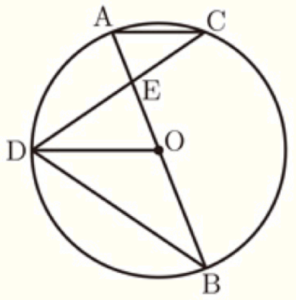
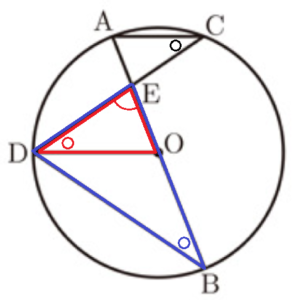
下の図のように,線分 \( AB \) を直径とする円 \( O \) の周上に,直線 \( AB \) に対して反対側にある2点 \( C,D \) を \( AC//DO \) となるようにとる。また,線分 \( AB \) と線分 \( CD \) との交点を \( E \) とする。
このとき,次の (1),(2) の問いに答えなさい。
(1) \( △EDO \) ∽ \( △EBD \) となることを証明しなさい。
【解答】
\( △EDO \) と \( △EBD \) において,
\( AC//DO \) より,錯角が等しいので,\( ∠ACD=∠EDO \) ・・・ ➀
弧 \( AD \) の円周角なので,\( ∠ACD=∠EBD \) ・・・ ➁
➀➁より,\( ∠EDO=∠EBD \) ・・・ ➂
\( ∠E \) は共通 ・・・ ➃
➂➃より,2組の角がそれぞれ等しいので,\( △EDO \) ∽ \( △EBD \)
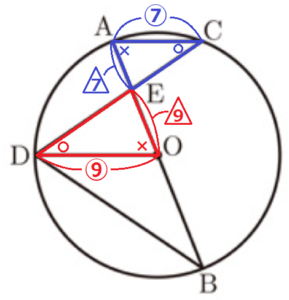
(2) \( AC:DO=7:9 \) であるとき,\( △EDO \) と \( △EBD \) の相似比を求めなさい。
【解説】
\( △ACE \) と \( △EDO \) において,
\( AC//DO \) より,錯角が等しいので,
\( ∠ACE=∠ODE \) ・・・ ➀
\( ∠CAE=∠DOE \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △ACE \) ∽ \( △EDO \)
\( AC:DO=7:9 \) より,相似比は \( 7:9 \)
よって,\( EA:EO=7:9 \)
\( BO,OA \) は円 \( O \) の半径なので,\( BO=OA=EA+EO \) より,
\( EO:BO=EO:EA+EO=9:(7+9)=9:16 \)
ここから,
\( EO:EB=EO:EO+BO=9:(16+9)=9:25 \)
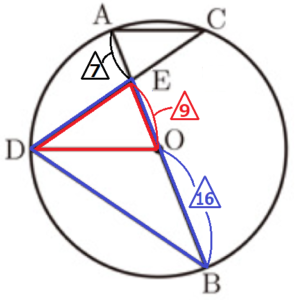
\( △EDO \) の底辺を線分 \( EO \),\( △EBD \) の底辺を線分 \( EB \) とすると,
高さが共通になっているので,底辺の長さの比が面積比になります。
ここから,\( △EDO \) と \( △EBD \) の面積比は,
\( △EDO:△EBD=EO:EB=9:25=3^2:5^2 \)
相似な三角形の面積比は相似比の2乗の比と等しいので,
\( △EDO \) と \( △EBD \) の相似比は,\( 3:5 \)
大問6
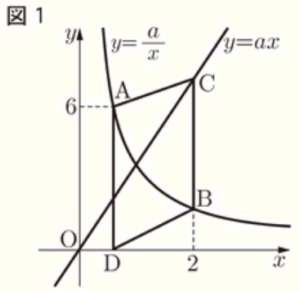
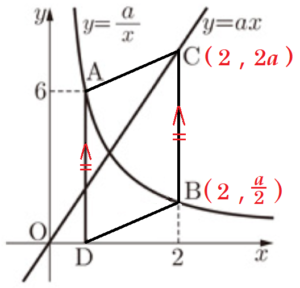
図1のように,反比例 \( y=\dfrac{a}{x} \;\; (x>0) \) のグラフ上に2点 \( A,B \) があり,\( A \) の \( y \) 座標は \( 6 \),\( B \) の \( x \) 座標は \( 2 \) である。また,比例 \( y=ax \) のグラフ上に点 \( C \),\( x \) 軸上に点 \( D \) があり,\( A \) と \( D \) の \( x \) 座標,\( B \) と \( C \) の \( x \) 座標はそれぞれ等しい。ただし,\( 0<a<12 \) とする。
次の[会話]は,花子さんと太郎さんが四角形 \( ADBC \) について考察し,話し合った内容である。
[会話]
花子さん:\( a \) の値を1つとると,2つのグラフが定まり,4つの辺と面積も定まるね。
点 \( A \) の座標は,反比例の関係 \( xy=a \) から求めることができそうだよ。
太郎さん:例えば,\( a=1 \) のときの四角形について調べてみようか。
・・・・・
太郎さん:形を見ると,いつでも台形だね。平行四辺形になるときはあるのかな?
花子さん:私は,面積についても調べてみたよ。そうしたら,\( \underline{a=1} \) のときと面積が等しくなる四角形が
他にもう1つあることがわかったよ。
このとき,次の (1)~(3) の問いに答えなさい。
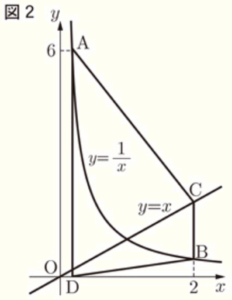
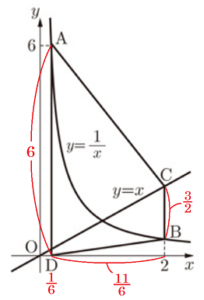
(1) 図2は,図1において,\( a=1 \) とした場合を表している。このとき,線分 \( BC \) の長さを求めなさい。
【解説】
\( a=1 \),点 \( B \) の \( x \) 座標は \( 2 \) なので,
反比例の関係 \( xy=a \) より,
\( 2 \times y=1 \)
\( y=\dfrac{1}{2} \)
点 \( C \) は直線 \( y=x \) 上の点で,\( x \) 座標は \( 2 \) なので,\( y=2 \)
よって,線分 \( BC \) の長さは,\( BC=2-\dfrac{1}{2}=\dfrac{3}{2} \)
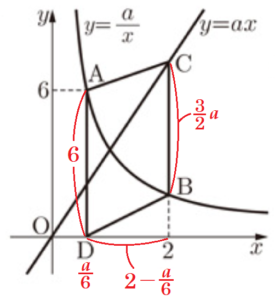
(2) 四角形 \( ADBC \) が平行四辺形になるときの \( a \) の値を求めなさい。
【解説】
平行四辺形の条件の1つ「向かい合う1組の辺が平行で長さが等しい」から,
\( AD=BC \) であるとき,つまり,\( BC=6 \) であるとき,四角形 \( ADBC \) が平行四辺形になります。
点 \( B \) は \( y=\dfrac{a}{x} \) 上の点なので,\( y \) 座標は,\( y=\dfrac{a}{2} \)
点 \( C \) は \( y=ax \) 上の点なので,\( y \) 座標は,\( y=2a \)
と表すことができます。
よって,\( BC=6 \) であるとき,
\( 2a-\dfrac{a}{2}=6 \)
\( \dfrac{3}{2}a=6 \)
\( 3a=12 \)
\( a=4 \)
(3) [会話]の下線部について,四角形 \( ADBC \) の面積が \( a=1 \) のときの面積と等しくなるような \( a \) の値を,\( a=1 \) の他に求めなさい。
【解説】
まず,\( a=1 \) のときの四角形 \( ADBC \) の面積を求めます。
点 \( A \) の \( y \) 座標は \( 6 \) なので,
反比例の関係 \( xy=a \) より,
\( x \times 6=1 \)
\( x=\dfrac{1}{6} \)
ここから,四角形 \( ADBC \) の高さは,
\( 2-\dfrac{1}{6}=\dfrac{11}{6} \) になります。
よって,\( BC=\dfrac{3}{2},AD=6 \),高さ \( =\dfrac{11}{6} \) より,
四角形 \( ADBC=\left( \dfrac{3}{2}+6 \right) \times \dfrac{11}{6} \times \dfrac{1}{2} \)
\( =\dfrac{55}{8} \)
次に,\( a=1 \) 以外のときの四角形 \( ADBC \) の面積を \( a \) を使って表します。
点 \( A \) の \( y \) 座標は \( 6 \) なので,
反比例の関係 \( xy=a \) より,
\( x \times 6=a \)
\( x=\dfrac{a}{6} \)
ここから,四角形 \( ADBC \) の高さは,\( 2-\dfrac{a}{6} \) と表せます。
また,(2) より,\( BC \) の長さは,\( 2a-\dfrac{a}{2}=\dfrac{3}{2}a \) と表せるので,
四角形 \( ADBC=\left( \dfrac{3}{2}a+6 \right) \times \left( 2-\dfrac{a}{6} \right) \times \dfrac{1}{2} \)
\( =\dfrac{(3a+12)(12-a)}{24} \)
\( =\dfrac{(a+4)(12-a)}{8} \)
四角形 \( ADBC \) の面積が等しくなるとき,
\( \dfrac{(a+4)(12-a)}{8}=\dfrac{55}{8} \)
\( (a+4)(12-a)=55 \)
\( -a^2+8a+48=55 \)
\( a^2-8a+7=0 \)
\( (a-1)(a-7)=0 \)
\( a=1,7 \)
\( a=1 \) の他を求めるので,あてはまるのは,\( a=7 \)
大問7
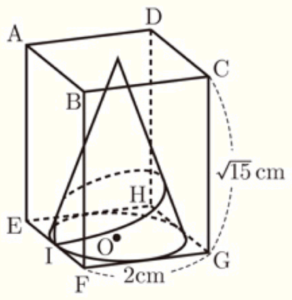
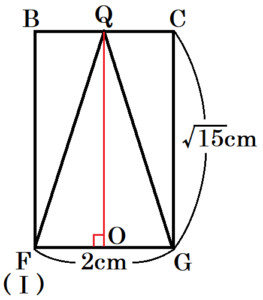
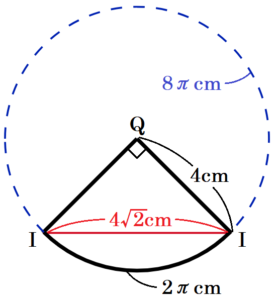
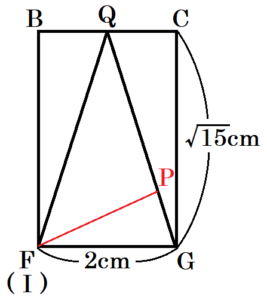
下の図のように,底面が1辺 \( 2 \; cm \) の正方形で,高さが \( \sqrt{15} \; cm \) の正四角柱と,正方形 \( EFGH \) のすべての辺に接する円 \( O \) を底面とする円錐があり,それらの高さは等しい。また,線分 \( EF \) と円 \( O \) との接点 \( I \) から円錐の側面にそって1周して \( I \) にもどるひもが,最も短くなるようにかけられている。ただし,円錐において,頂点と点 \( O \) を結ぶ線分は底面に垂直である。
このとき,次の (1)~(3) の問いに答えなさい。
(1) 円錐の母線の長さを求めなさい。
【解説】
この正四角柱と円錐を面 \( BFGC \) が正面になるように見ると,右の図のようになります。
円錐の頂点と正四角柱の接点を \( Q \) とすると,線分 \( QF(QI) \) が母線になります。
\( △OQF \) において,三平方の定理より,
\( QF^2=OQ^2+OF^2=( \sqrt{15})^2+1^2=16 \)
\( QF=4 \; (cm) \) ( \( QF>0 \)より )
(2) ひもの長さを求めなさい。ただし,ひもの太さや伸び縮みは考えないものとする。
【解答】
\( 4\sqrt{2} \; cm \)
【解説】
円錐の側面を線分 \( QI \) で切って展開すると,
半径 \( 4 \; cm \) のおうぎ形になります。
このおうぎ形の弧の長さは底面である
直径 \( 2 \; cm \) の円周の長さと等しいので,
\( 2\pi{} \; cm \)
半径 \( 4 \; cm \) の円周の長さは \( 8\pi{} \; cm \) なので,
おうぎ形の中心角の大きさは \( 360° \times \dfrac{2\pi{}}{8\pi{}}=90° \)
ここで, \( △QII \) は直角二等辺三角形なので,
ひもの長さは,\( 4\sqrt{2} \; cm \)
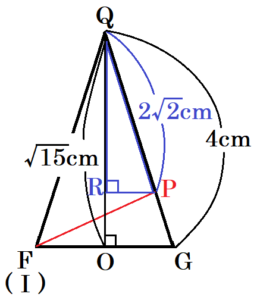
(3) ひもの通る線上に点 \( P \) をとる。\( P \) を頂点とし,四角形 \( ABCD \) を底面とする四角錐の体積が最も小さくなるとき,その体積を求めなさい。
【解答】
\( \dfrac{2\sqrt{30}}{3} \; cm^3 \)
【解説】
四角錐の体積が最も小さくなるのは,点 \( P \) と四角形 \( ABCD \) の距離が最も小さくなるときなので,線分 \( PQ \) の長さが最も短くなるときであるともいえます。
線分 \( PQ \) の長さが最も短くなるのは,円錐の側面の展開図において,線分 \( PQ \) とひもが垂直に交わるときなので,
\( △PQI \) は斜辺が \( 4 \; cm \) の直角二等辺三角形になります。
よって,\( PQ=\dfrac{4}{\sqrt{2}}=2\sqrt{2} \; (cm) \)
ここで,点 \( P \) から線分 \( QO \) に垂線をひき,交点を \( R \) とすると,\( △QPR \) ∽ \( △QGO \) なので,
\( QP:QG=QR:QO \)
\( 2\sqrt{2}:4=QR:\sqrt{15} \)
\( 4QR=2\sqrt{30} \)
\( QR=\dfrac{\sqrt{30}}{2} \; (cm) \)
以上より,四角錐の体積は,
\( 2 \times 2 \times \dfrac{\sqrt{30}}{2} \times \dfrac{1}{3}=\dfrac{2\sqrt{30}}{3} \; (cm^3) \)