大問1
(1) 次の計算をしなさい。
ア \( -8+27 \div (-9) \)
【解説】
\( =-8-3 \)
\( =-11 \)
イ \( (-6a)^2 \times 9b \div 12ab \)
【解説】
\( =\dfrac{36a^2 \times 9b}{12ab} \)
\( =27a \)
ウ \( \dfrac{2x+y}{3}-\dfrac{x+5y}{7} \)
【解答】
\( \dfrac{11x-8y}{21} \)
【解説】
\( =\dfrac{7(2x+y)}{21}-\dfrac{3(x+5y)}{21} \)
\( =\dfrac{14x+7y-3x-15y}{21} \)
\( =\dfrac{11x-8y}{21} \)
エ \( \sqrt{45}+\dfrac{10}{\sqrt{5}} \)
【解説】
\( =3\sqrt{5}+\dfrac{10 \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}} \)
\( =3\sqrt{5}+2\sqrt{5} \)
\( =5\sqrt{5} \)
(2) \( a=41,b=8 \) のとき, \( a^2-25b^2 \) の式の値を求めなさい。
【解説】
与式\( =(a+5b)(a-5b) \)
\( a=41,b=8 \) を代入すると,
\( =(41+5 \times 8)(41-5 \times 8) \)
\( =81 \times 1 \)
\( =81 \)
(3) 次の2次方程式を解きなさい。
\( x^2+7x=2x+24 \)
【解説】
\( x^2+7x=2x+24 \)
\( x^2+5x-24=0 \)
\( (x-3)(x+8)=0 \)
\( x=3,-8 \)
大問2
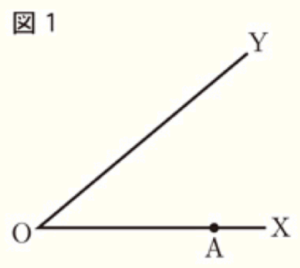
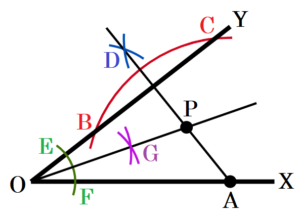
(1) 図1において,点 \( A \) は辺 \( OX \) 上の点である。点 \( A \) から辺 \( OY \) に引いた垂線上にあり,2辺 \( OX,OY \) から等しい距離にある点 \( P \) を作図しなさい。ただし,作図には定規とコンパスを使用し,作図に用いた線は残しておくこと。
【解答】
手順1 点 \( A \) を中心に円弧を描く
(辺 \( OY \) との交点を点 \( B,C \) とします。)
手順2 点 \( B,C \) を中心に円弧を描く
(交点を点 \( D \) とします。)
手順3 2点 \( A,D \) を通る直線を描く
手順4 点 \( O \) を中心に円弧を描く
(辺 \( OY,OX \) との交点を点 \( E,F \) とします。)
手順5 点 \( E,F \) を中心に円弧を描く
(交点を点 \( G \) とします。)
手順6 2点 \( O,G \) を通る直線を描く
手順3と手順6の直線の交点が求める点 \( P \) になります。
(2) 次の の中に示したことがらの逆を書きなさい。
\( a \) も \( b \) も正の数ならば,\( a+b \) は正の数である。
また,
の中のことがらは正しいが,逆は正しくない。
の中のことがらの逆が正しくないことを示すための反例を1つ書きなさい。
【解答】
逆 ・・・ \( a+b \) が正の数ならば,\( a \) も \( b \) も正の数である。
反例 ・・・ \( a=2,b=-1 \)
【解説】
あることがら 「 \( A \) ならば \( B \) 」 の逆は「 \( B \) ならば \( A \) 」 になります。
(3) 2つの袋Ⅰ,Ⅱがあり,袋Ⅰには \( 2,3,4,5 \) の数字を1つずつ書いた4枚のカードが,袋Ⅱには \( 6,7,8,9,10 \) の数字を1つずつ書いた5枚のカードが入っている。図2は,袋Ⅰと袋Ⅱに入っているカードを示したものである。
2つの袋Ⅰ,Ⅱからそれぞれ1枚のカードを取り出すとき,袋Ⅱから取り出したカードに書いてある数が,袋Ⅰから取り出したカードに書いてある数の倍数である確率を求めなさい。ただし,袋Ⅰからカードを取り出すとき,どのカードが取り出されることも同様に確からしいものとする。また,袋Ⅱについても同じように考えるものとする。
【解説】
袋Ⅰと袋Ⅱから取り出したカードの組み合わせを樹形図として書き,袋Ⅱから取り出したカードに
書いてある数が,袋Ⅰから取り出したカードに書いてある数の倍数であるところに
○ をつけます。
あてはまるのは,7通り,すべての組み合わせは20通りなので,確率は,\( \dfrac{7}{20} \)

大問3
あるクラスの10人の生徒A~Jが,ハンドボール投げを行った。表1は,その記録を表したものである。図3は,表1の記録を箱ひげ図に表したものである。
このとき,次の (1),(2) の問いに答えなさい。

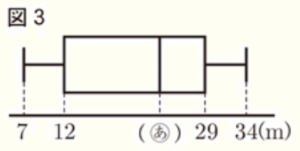
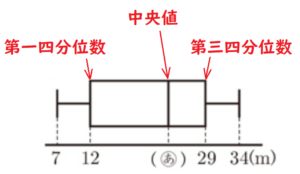
(1) 図3の ( あ ) に適切な値を補いなさい。また,10人の生徒A~Jの記録の四分位範囲を求めなさい。
【解答】
( あ ) ・・・ \( 24 \)
四分位範囲 ・・・ \( 17 \)
【解説】
( あ ) は中央値になります。
10人の記録をまとめたものなので,
中央値は距離の短い方から5番目と6番目の人の値の平均値になります。
距離の短い順に並べ替えると次のようになるので,
中央値は,\( \dfrac{23+25}{2}=24 \; (m) \) 。

四分位範囲は,第三四分位数 \( – \) 第一四分位数 で求めることができるので,
四分位範囲は,\( 29-12=17 \; (m) \) になります。
(2) 後日,生徒Kもハンドボール投げを行ったところ,Kの記録は \( a \; m \) だった。図4は,11人の生徒A~Kの記録を箱ひげ図に表したものである。
このとき,\( a \) がとりうる値をすべて求めなさい。ただし,\( a \) は整数とする。

【解説】
11人の生徒の記録を箱ひげ図にすると,
第一四分位数は3番目,中央値は6番目,第三四分位数は9番目の人の値になります。
まず,A~Jの記録を距離の短い順に並べ替え,箱ひげ図からわかる第一四分位数 \( 12 \; m \) ,
中央値 \( 25 \; m \) ,第三四分位数 \( 32 \; m \) のところに印をつけると,次のようになります。
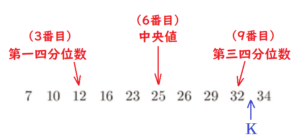
ここで,第一四分位数が3番目,中央値が6番目,第三四分位数が9番目の人の値になるのは,
\( 32 \) と \( 34 \) の間にKの記録があるときなので,あてはまる \( a \) の値は,\( 32,33,34 \) 。
(最大値が \( 34 \; m \) なので,\( 35 \; m \) 以上にはなりません。)
大問4
ある中学校の生徒会が,ボランティア活動で鉛筆とボールペンを集め,2つの団体S,Tへ送ることにした。
団体Sは鉛筆のみを,団体Tは鉛筆とボールペンの両方を受け付けていた。
この活動で,鉛筆はボールペンの2倍の本数を集めることができた。鉛筆については,集めた本数の80%を
団体Sへ,残りを団体Tへ送った。また,ボールペンについては,集めた本数の4%はインクが出なかったため,それらを除いた残りを団体Tへ送った。団体Tへ送った鉛筆とボールペンの本数の合計は,団体Sへ送った鉛筆の本数よりも18本少なかった。
このとき,集めた鉛筆の本数とボールペンの本数は,それぞれ何本であったか。方程式をつくり,計算の過程を書き,答えを求めなさい。
【解答】
集めた鉛筆の本数を \( x \) 本,ボールペンの本数を \( y \) 本とすると,
\( \left\{ \begin{array}{}
x=2y \;\; ・・・ \;\; ① \\
\dfrac{80}{100}x-18=\dfrac{20}{100}x+\dfrac{96}{100}y \;\; ・・・ \;\; ② \\
\end{array} \right. \)
②\( \; \times 25 \) すると
\( 15x-24y=450 \) ・・・ ②’
① を ②’に代入すると,
\( 15 \times 2y-24y=450 \)
\( 6y=450 \)
\( y=75 \)
➀に代入すると,
\( x=2 \times 75 \)
\( =150 \)
よって,集めた鉛筆の本数は \( 150 \) 本,ボールペンの本数は \( 75 \) 本
大問5
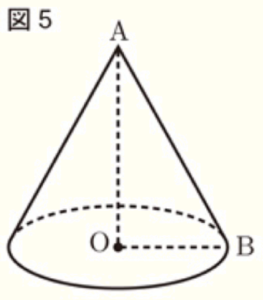
図5の立体は,円 \( O \) を底面とする円すいである。この円すいにおいて,底面の半径は \( 3 \; cm \),母線 \( AB \) の長さは \( 6 \; cm \) である。また,線分 \( OA \) と底面は垂直である。
このとき,次の (1)~(3) の問いに答えなさい。
(1) 次のア~オの5つの投影図のうち,1つは円すいの投影図である。円すいの投影図を,ア~オの中から1つ選び,記号で答えなさい。
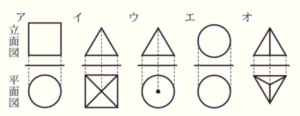
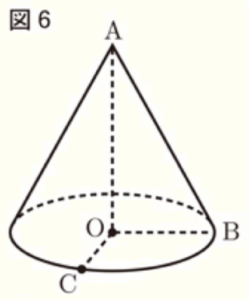
(2) この円すいにおいて,図6のように,円 \( O \) の円周上に \( ∠BOC=110° \) となる点 \( C \) をとる。小さい方の弧 \( BC \) の長さを求めなさい。ただし,円周率は \( \pi{} \) とする。
【解答】
\( \dfrac{11}{6}\pi{} \; cm \)
【解説】
\( 2\pi{} \times 3 \times \dfrac{110°}{360°}=\dfrac{11}{6}\pi{} \; (cm) \)
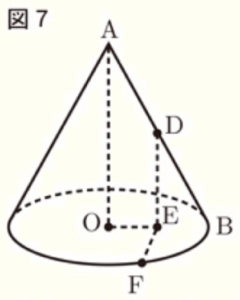
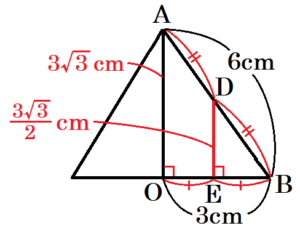
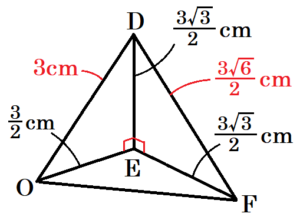
(3) この円すいにおいて,図7のように,\( AB \) の中点を \( D \) とし,点 \( D \) から底面に引いた垂線と底面との交点を \( E \) とする。また,円 \( O \) の円周上に \( ∠OEF=90° \) となる点 \( F \) をとる。\( △ODF \) の面積を求めなさい。
【解答】
\( \dfrac{9\sqrt{15}}{8} \; cm^2 \)
【解説】
この円すいを正面から見ると,\( △AOB \) は,\( AB:OB=6:3=2:1 \) の直角三角形なので,
\( OA:OB=\sqrt{3}:1 \)
\( OA:3=\sqrt{3}:1 \)
\( OA=3\sqrt{3} \; (cm) \)
また,\( △AOB \) ∽ \( △DEB \) で,\( D \) は \( AB \) の中点なので,
相似比は \( 1:2 \) であり,
\( OE=\dfrac{1}{2}OB=\dfrac{3}{2} \; (cm),ED=\dfrac{1}{2}OA=\dfrac{3\sqrt{3}}{2} \; (cm) \),
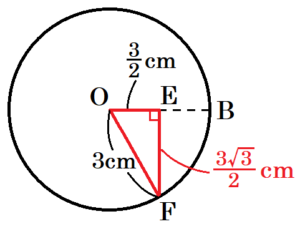
この円すいの底面に注目すると,\( △OEF \) は,\( OE:OF=3:\dfrac{3}{2}=2:1 \) の直角三角形なので,
\( EF:OE=\sqrt{3}:1 \)
\( EF:\dfrac{3}{2}=\sqrt{3}:1 \)
\( EF=\dfrac{3\sqrt{3}}{2} \; (cm) \)
次に,三角すい \( D-FOE \) に注目すると,
\( △DEF \) は,\( ED=EF \) の直角二等辺三角形なので,
\( DF= \sqrt{2}EF=\dfrac{3\sqrt{6}}{2} \; cm \)
\( △ODE \) は,\( OE:ED=\dfrac{3}{2}:\dfrac{3\sqrt{3}}{2}=1:\sqrt{3} \) の
直角三角形なので,
\( OD=2OE=3 \; (cm) \)
次に,\( △ODF \) に注目すると,
\( OD=OF \) の二等辺三角形なので,
\( O \) から \( DF \) に垂線をひき,交点を \( G \) とすると,
\( △OFG \) は直角三角形になります。
三平方の定理より,
\( OG^2=OF^2-FG^2 \)
\( =3^2-\left( \dfrac{3\sqrt{6}}{4} \right)^2 \)
\( =9-\dfrac{54}{16} \)
\( =\dfrac{90}{16} \)
\( OG=\dfrac{3\sqrt{10}}{4} \; (cm) \)
よって,
\( △ODF=DF \times OG \times \dfrac{1}{2} \)
\( =\dfrac{3\sqrt{6}}{2} \times \dfrac{3\sqrt{10}}{4} \times \dfrac{1}{2} \)
\( =\dfrac{9\sqrt{15}}{8} \; (cm^2) \)
大問6
次の の中の文は,授業でT先生が示した資料である。
このとき,次の (1)~(3) の問いに答えなさい。
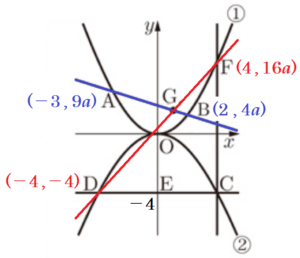
図8において,① は関数 \( y=ax^2 \;\; (a>0) \) のグラフであり,
➁ は関数 \( y=bx^2 \;\; (b<0) \) のグラフである。 2点 \( A,B \) は,放物線 ① 上の点であり,その \( x \) 座標は,それぞれ \( -3,2 \) である。点 \( C \) は,放物線 ➁ 上の点であり,その座標は \( (4,-4) \) である。点 \( C \) を通り \( x \) 軸に平行な直線と放物線 ➁ との交点を \( D \) とし,直線 \( CD \) と \( y \) 軸との交点を \( E \) とする。点 \( C \) を通り \( y \) 軸に平行な直線と放物線 ① との交点を \( F \) とする。また,点 \( G \) は直線 \( AB \) 上の点であり,その \( x \) 座標は \( 1 \) である。
RさんとSさんは,タブレット型端末を使いながら,
図8のグラフについて話している。
Rさん:関数 \( y=bx^2 \) の比例定数 \( b \) の値は求められるね。
Sさん:➁ は点 \( C \) を通るから \( b \) の値は ( あ ) だよ。
Rさん:関数 \( y=ax^2 \) の \( a \) の値は決まらないね。
Sさん:タブレット型端末を使うと,(ア)\( a \) の値を変化させたときのグラフや図形の変化する
ようすが分かるよ。
Rさん:そうだね。(イ)3点 \( D,G,F \) が一直線上にある場合もあるよ。
Sさん:本当だね。計算で確認してみよう。
(1) ( あ ) に適切な値を補いなさい。
【解説】
\( y=bx^2 \) に \( x=4,y=-4 \) を代入すると,
\( -4=b \times 4^2 \)
\( 16b=-4 \)
\( b=-\dfrac{1}{4} \)
(2) (ア) のときの,グラフや図形の変化するようすについて述べたものとして正しいものを,次の ア~オ の中からすべて選び,記号で答えなさい。
ア \( a \) の値を大きくすると,① のグラフの開き方は小さくなる。
イ \( a \) の値を小さくすると,点 \( A \) の \( y \) 座標から点Bの \( y \) 座標をひいた値は大きくなる。
ウ \( a \) の値を大きくすると,\( △OBE \) の面積は大きくなる。
エ \( a \) の値を小さくすると,直線 \( OB \) の傾きは小さくなる。
オ \( a \) の値を大きくすると,線分 \( CF \) の長さは短くなる。
【解説】
イ \( y=ax^2 \) において,点 \( A \) の \( y \) 座標は \( 9a \),点 \( B \) の \( y \) 座標は \( 4a \) と表すことができるので,
点 \( A \) の \( y \) 座標から点 \( B \) の \( y \) 座標をひいた値は,\( 5a \) となります。
よって,\( a \) の値を小さくすると,小さくなります。
ウ \( △OBE \) の底辺を \( OE \) とすると,点 \( B \) の \( x \) 座標の値が高さになります。
\( a \) の値を変えても,\( OE \) の長さと点 \( B \) の \( x \) 座標の値はどちらも変わらないので,
\( △OBE \) の面積も変わりません。
オ \( y=ax^2 \) において,点 \( F \) の \( y \) 座標は \( 16a \) と表すことができるので,
線分 \( CF \) の長さは,\( 16a-(-4)=16a+4 \) と表すことができます。
よって,\( a \) の値を大きくすると,線分 \( CF \) の長さは長くなります。
(3) (イ) のときの \( a \) の値を求めなさい。求める過程も書きなさい。
【解答】
\( a=\dfrac{3}{10} \)
【解説】
点 \( G \) は,直線 \( DF \) と \( AB \) の交点で,\( x \) 座標の値は \( 1 \) とわかっているので,
2直線の式を使って,点 \( G \) の \( y \) 座標の値を \( a \) を使って2パターン表します。
このとき,2パターンで表した \( y \) 座標の値は等しくなるのでそれを利用して \( a \) の値を求めます。
【直線 \( DF \) 上の点として表す】
\( D(-4,-4),F(4,16a) \) なので,
直線 \( DF \) の傾きは,\( \dfrac{16a-(-4)}{4-(-4)}=\dfrac{4a+1}{2} \)
直線 \( DF \) の式を \( y=\dfrac{4a+1}{2}x+b \) とすると,\( (-4,-4) \)を通るので,
\( -4=\dfrac{4a+1}{2} \times (-4)+b \)
\( -4=-8a-2+b \)
\( b=8a-2 \)
よって,
直線 \( DF \) の式は \( y=\dfrac{4a+1}{2}x+8a-2 \)
点 \( G \) は,直線 \( DF \) 上の点で,\( x \) 座標の値は \( 1 \) なので,
点 \( G \) の \( y \) 座標の値は
\( y=\dfrac{4a+1}{2} \times 1+8a-2=\dfrac{20a-3}{2} \) ・・・ ①
【直線 \( AB \) 上の点として表す】
\( A(-3,9a),B(2,4a) \) と表せるので,
直線 \( AB \) の傾きは,\( \dfrac{4a-9a}{2-(-3)}=-a \)
直線 \( AB \) の式を \( y=-ax+c \) とすると,
\( (2,4a) \)を通るので,
\( 4a=-a \times 2+c \)
\( c=6a \)
よって,直線 \( AB \) の式は \( y=-ax+6a \)
点 \( G \) は,直線 \( AB \) 上の点で,\( x \) 座標の値は \( 1 \) なので,
点 \( G \) の \( y \) 座標の値は
\( y=-a \times 1+6a=5a \) ・・・ ➁
➀➁ は,同じ点 \( G \) の \( y \) 座標を表しているので,
\( \dfrac{20a-3}{2}=5a \)
\( 20a-3=10a \)
\( 10a=3 \)
\( a=\dfrac{3}{10} \)
大問7
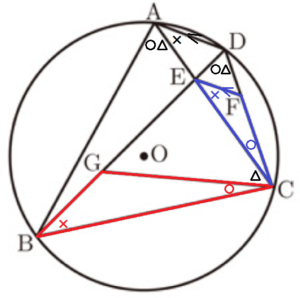
図9において,4点 \( A,B,C,D \) は円 \( O \) の円周上の点であり,\( △ABC \) は \( BA=BC \) の二等辺三角形である。\( AC \) と \( BD \) との交点を \( E \) とし,点 \( E \) を通り \( AD \) に平行な直線と \( CD \) との交点を \( F \) とする。
また,\( BD \) 上に \( GC=GD \) となる点 \( G \) をとる。
このとき,次の (1),(2) の問いに答えなさい。
(1) \( △BCG \) ∽ \( △ECF \) であることを証明しなさい。
【解答】
\( △BCG \) と \( △ECF \) において,
\( △ABC \) は \( BA=BC \) の二等辺三角形なので,
\( ∠BCA=∠BAC \) ・・・ ➀
\( △DGC \) は \( GC=GD \) の二等辺三角形なので,
\( ∠GCD=∠GDC \) ・・・ ➁
弧 \( BC \) に対する円周角なので,
\( ∠BAC=∠GDC \) ・・・ ➂
➀➁➂より,\( ∠BCA=∠GCD \) ・・・ ➃
\( ∠BCA=∠BCG+∠GCE \) ・・・ ➄
\( ∠GCD=∠ECF+∠GCE \) ・・・ ➅
➃➄➅より,\( ∠BCG=∠ECF \) ・・・ ➆
弧 \( CD \) に対する円周角なので,
\( ∠CBG=∠CAD \) ・・・ ➇
\( AD//EF \) より,同位角は等しいので,
\( ∠CAD=∠CEF \) ・・・ ➈
➇➈より,\( ∠CBG=∠CEF \) ・・・ ➉
➆➉より,2組の角がそれぞれ等しいので,
\( △BCG \) ∽ \( △ECF \)
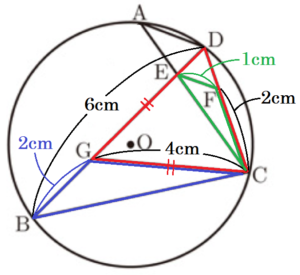
(2) \( GC=4 \; cm,BD=6 \; cm,CF=2 \; cm \) のとき,\( GE \) の長さを求めなさい。
【解答】
\( \dfrac{13}{4} \; cm \)
【解説】
\( GC=GD=4 \; cm,BD=6 \; cm \) より,
\( BG=BD-GD=2 \; (cm) \)
(1) より,\( △BCG \) ∽ \( △ECF \) なので,
\( BG:EF=GC:FC \)
\( 2:EF=4:2 \)
\( EF=1 \; (cm) \)
\( △ABC \) と \( △DFE \) において,
弧 \( BC \) に対する円周角なので,
\( ∠BAC=∠EDF \) ・・・ ➀
弧 \( AB \) に対する円周角なので,
\( ∠BCA=∠BDA \) ・・・ ➁
\( AD//EF \) より,錯角は等しいので,
\( ∠BDA=∠FED \) ・・・ ➂
➁➂より,\( ∠BCA=∠FED \) ・・・ ➃
➀➃より,2組の角がそれぞれ等しいので,
\( △ABC \) ∽ \( △DFE \)
\( △ABC \) は二等辺三角形なので,\( △DFE \) も二等辺三角形であり,
\( DF=EF=1 \; cm \)
\( △DGC \) と \( △DFE \) において,
\( ∠D \) は共通 ・・・ ➀
\( △DGC \) は二等辺三角形なので,
\( ∠GCD=∠GDC \) ・・・ ➁
\( △DFE \) は二等辺三角形なので,
\( ∠FED=∠GDC \) ・・・ ➂
➁➂より,\( ∠GCD=∠FED \) ・・・ ➃
➀➃より,2組の角がそれぞれ等しいので,
\( △DGC \) ∽ \( △DFE \)
よって,
\( GC:FE=DC:DE \)
\( GC:FE=(DF+CF):DE \)
\( 4:1=(1+2):DE \)
\( 4DE=3 \)
\( DE=\dfrac{3}{4} \; (cm) \)
\( GE=GD-DE=4-\dfrac{3}{4}=\dfrac{13}{4} \; (cm) \)