大問1
(1) \( (-5)+(-2) \) を計算しなさい。
【解説】
\( =-5-2 \)
\( =-7 \)
(2) \( 3(a+b)-2 (a-b) \) を計算しなさい。
【解説】
\( =3a+3b-2a+2b \)
\( =a+5b \)
(3) \( 4\sqrt{2} \times 2\sqrt{3} \) を計算しなさい。
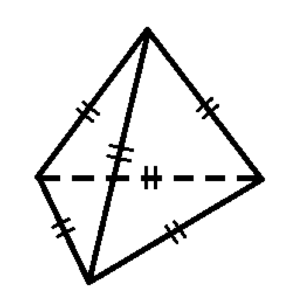
(4) 正四面体の辺の数を答えなさい。
【解説】
正四面体は,すべての班の長さが等しい三角すいなので,辺の長さは \( 6 \) 本になります。
(5) \( 4x^2-9y^2 \) を因数分解しなさい。
【解答】
\( (2x+3y)(2x-3y) \)
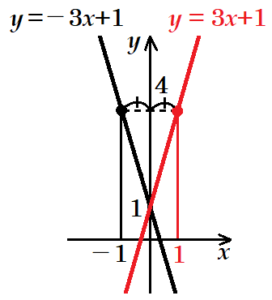
(6) \( y \) 軸を対称の軸として, 直線 \( y=-3x+1 \) と線対称となる直線の式を求めなさい。
【解説】
直線 \( y=-3x+1 \) は,
\( (x,y)=(0,1),(-1,4) \) を通ります。
\( (x,y)=(-1,4) \) の点を \( y \) 軸を対称の軸として移動させると,\( (x,y)=(1,4) \) に移動します。
また,\( (x,y)=(0,1) \) は,
直線 \( y=-3x+1 \) と \( y \) 軸の交点なので
移動しません。
よって,求める直線は,
2点 \( (0,1),(1,4) \) を通る直線なので,
\( y=3x+1 \)
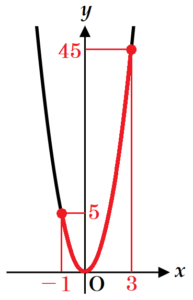
(7) 関数 \( y=5x^2 \) について,\( x \) の変域が \( -1≦x≦3 \) のときの \( y \) の変域を求めなさい。
【解説】
\( y=ax^2 \;\;(a>0) \) において,
\( x \) の変域が \( 0 \) を含むとき,
\( y \) の最小値は \( 0 \) になります。
また,\( x \) の絶対値が最大になるとき,
\( y \) の値も最大になります。
\( -1≦x≦3 \) のとき,
\( 0 \) を含んでいるので,最小値は \( 0 \),
絶対値が最大になるのは \( x=3 \) のときなので,
\( y \) の値は,\( y=5 \times 3^2=45 \)
よって,\( y \) の変域は,\( 0≦y≦45 \)
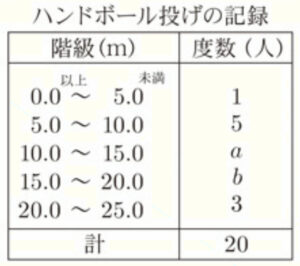
(8) 右の表は,ある中学校の女子 \( 20 \) 人のハンドボール投げの記録を度数分布表に整理したものである。この表から求めた最頻値が \( 12.5 \; m \) であるとき,\( a,b \) にあてはまる数の組み合わせは全部で何通りあるか,求めなさい。
【解説】
すべての階級の度数の合計が \( 20 \) 人なので,
\( 1+5+a+b+3=20 \)
\( a+b=11 \) ・・・ ➀
最頻値が \( 12.5 \; m \) であることから,
最頻値が含まれる階級は,「\( 10 \; m \) 以上 \( 15 \; m \) 未満」になります。
ここから,\( a>b \) ・・・ ➁
➀➁を満たすような \( a,b \) の組み合わせは,
\( (a,b)=(6,5),(7,4),(8,3),(9,2),(10,1),(11,0) \)
の6通り
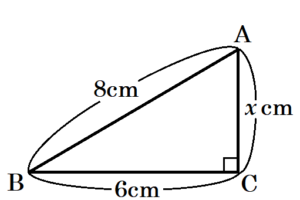
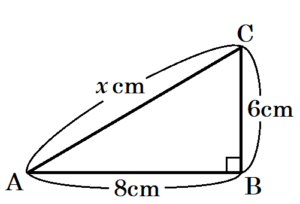
(9)\( △ABC \) において,\( AB=8 \; cm,BC=6 \; cm,CA=x \; cm \) である。\( △ABC \) が直角三角形になるときの \( x \) の値をすべて求めなさい。
【解答】
\( x=2\sqrt{7},10 \)
【解説】
直角三角形の3辺は,斜辺の長さが一番長くなります。
\( AB=8 \; cm,BC=6 \; cm,CA=x \; cm \) より,一番長くなる可能性があるのは,
\( AB=8 \; cm,CA=x \; cm \) のどちらかです。
【\( AB=8 \; cm \) が斜辺の場合】
三平方の定理より,
\( 8^2=6^2+x^2 \)
\( x^2=28 \)
\( x=2\sqrt{7} \; (cm) \) (\( AB>0 \) より)
【\( CA=x \; cm \) が斜辺の場合】
三平方の定理より,
\( x^2=8^2+6^2 \)
\( x^2=100 \)
\( x=10 \; (cm) \) (\( CA>0 \) より)
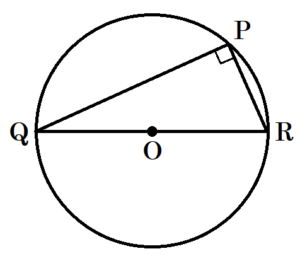
直角三角形は斜辺が一番長くなる理由
辺 \( QR \) を斜辺とする直角三角形 \( PQR \) において,
3つの頂点を通る円 \( O \) を考えると,
\( ∠QPR=90° \) より,直径に対する円周角になるので,
辺 \( QR \) は円 \( O \) の直径になっています。
1つの円の中で最も長い弦が直径になるので,
3辺の中で辺 \( QR \) が一番長いといえます。
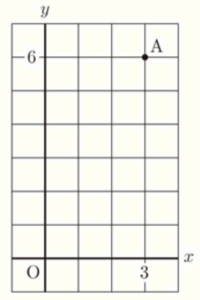
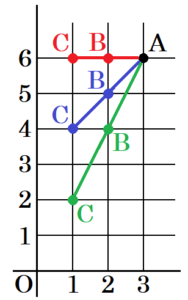
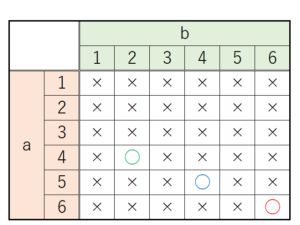
(10) 右の図のように,点 \( A (3,6) \) をとる。また,\( 1 \) から \( 6 \) までの目が出るさいころを2回投げて,最初に出た目の数を \( a \),2回目に出た目の数を \( b \) とし,2点 \( B (2,a),C(1,b) \) をとる。このとき,3点 \( A,B,C \) が1つの直線上に並ぶ確率を求めなさい。ただし,さいころはどの目が出ることも同様に確からしいものとする。
【解説】
3点 \( A,B,C \) が1つの直線上に並ぶのは,
\( B (2,6),C(1,6) \) つまり,\( a=6,b=6 \)
\( B (2,5),C(1,4) \) つまり,\( a=5,b=4 \)
\( B (2,4),C(1,2) \) つまり,\( a=4,b=2 \)
の3通りになっています。
さいころの出た目 \( a,b \) の組み合わせを表に書き出すと,
一直線上に並ぶのは3通り,すべての組み合わせは36通りなので,
求める確率は \( \dfrac{3}{36}=\dfrac{1}{12} \)
大問2
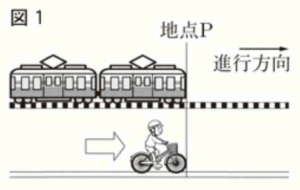
一直線にのびた線路と,その横に,線路に平行な道路がある。電車が駅に停車していると,あさひさんが乗った自転車が電車の後方から,電車の進行方向と同じ方向に走ってきた。図1のように,停車している電車の先端を地点 \( P \) とする。このとき,電車が地点 \( P \) を出発したのと同時に,自転車も地点 \( P \) を通過した。
電車が地点 \( P \) を出発してから \( x \) 秒間に電車と自転車が進む距離を \( y \; m \) とする。\( 0≦x≦30 \) のとき,電車は \( y=\dfrac{3}{10}x^2 \) の関係になり,自転車は \( y=6x \) の関係になることがわかっている。
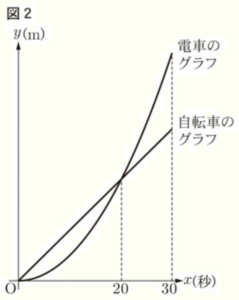
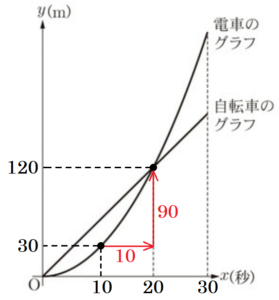
図2は,電車と自転車について,\( x \) と \( y \) の関係をグラフに表したものである。(1)~(4)に答えなさい。
(1) 電車が自転車に追いつくのは,地点 \( P \) から何 \( m \) 離れた地点か,求めなさい。
【解説】
電車が自転車に追いつく時間と場所は,グラフにおいて,直線と曲線の交点として表されます。
交点の \( x \) 座標の値は \( 20 \) なので,そのときの \( y \) 座標の値は,
\( y=6 \times 20=120 \; (m) \)
(2) 電車が地点 \( P \) を出発して \( 10 \) 秒後から \( 20 \) 秒後までの電車の平均の速さは秒速何 \( m \) か,求めなさい。
【解説】
出発して \( 10 \) 秒後の電車の位置は
\( y=\dfrac{3}{10} \times 10^2=30 \; (m) \)
なので,平均の速さは
\( \dfrac{120-30}{20-10}=9 \)
より,秒速 \( 9 \; m \)
(3) \( 0≦x≦20 \) のとき,自転車と電車が \( 30 \; m \) 離れるのは,電車が地点 \( P \) を出発してから何秒後か,求めなさい。
【解説】
出発してから \( t \) 秒後に自転車と電車が \( 30 \; m \) 離れるとすると,
\( t \) 秒後に自転車が進んだ距離は
\( y=6t \; (m) \)
\( t \) 秒後に電車が進んだ距離は
\( y=\dfrac{3}{10}t^2 \; (m) \)
と表せるので,
\( 6t-\dfrac{3}{10}t^2=30 \)
\( \dfrac{3}{10}t^2-6t+30=0 \)
\( t^2-20t+100=0 \)
\( (t-10)^2=0 \)
\( t=10 \)
よって,答えは 出発してから \( 10 \) 秒後
(4) 地点 \( P \) から \( 150 \; m \) 離れた地点において,電車が到達してから自転車が到達するまでにおよそ何秒かかるか,求め方を説明しなさい。 ただし,実際に何秒かかるかを求める必要はない。
【解答】
電車のグラフを表す式 \( y=\dfrac{3}{10}x^2 \) に \( y=150 \) を代入したときの \( x \) の値を \( x_1 \),
自転車のグラフを表す式 \( y=6x \) に \( y=150 \) を代入したときの \( x \) の値を \( x_2 \)
とすると,\( x_2-x_1 \) で求めることができる。
大問3
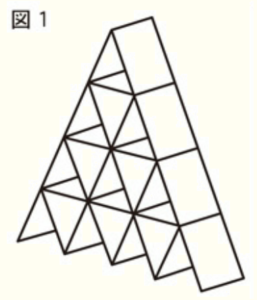
まことさんは,トランプを使って図1のようなタワーをつくろうと考えた。できるだけ大きなタワーをつくるために,必要なトランプの枚数を調べることにした。(1)・(2)に答えなさい。
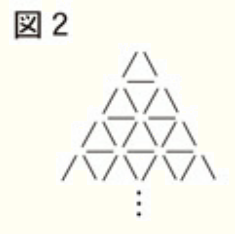
(1) まことさんは,図2のように,トランプの代わりに同じ長さの棒を並べたモデルをつくり,棒の本数を数えることでトランプの枚数を調べることにした。(a),(b)に答えなさい。
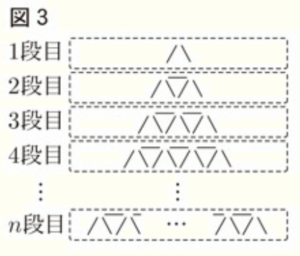
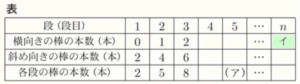
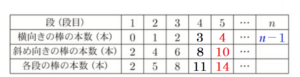
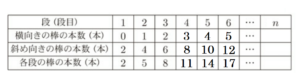
(a) まことさんは,図3のように,上から \( 1 \) 段目,\( 2 \) 段目,\( 3 \) 段目,\( 4 \) 段目,・・・ ,\( n \) 段目と分けて,各段の棒の本数を,横向きの棒と斜め向きの棒に着目して,下のような表にまとめようとしている。表の ( ア ) にあてはまる数を, イ にはあてはまる \( n \) を用いた式をそれぞれ書きなさい。
【解答】
( ア ) ・・・ \( 14 \) 本
イ ・・・ \( n-1 \) 本
【解説】
( ア )
図3から,横向きの棒の本数は,\( 0 → 1 → 2 → 3 \) となっているので,その次は \( 4 \)
斜め向きの棒の本数は, \( 2 → 4 → 6 → 8 \) となっているので,その次は \( 10 \)
よって,合計の本数は \( 14 \) 本。
イ
横向きの棒の本数は,段数より \( 1 \) 小さい数字が入っているので,
\( n \) 段目のときは,\( n-1 \) 本。
(b) トランプ \( 1 \) 組 \( 54 \) 枚を使うと最大何段のタワーをつくることができるか,求めなさい。ただし,使わないトランプがあってもよいものとする。
【解説】
(a)の表から各段数のタワーをつくるのに必要なトランプの枚数は,
\( 1 \) 段目 ・・・ \( 2 \) 本
\( 2 \) 段目 ・・・ \( 2+5=7 \) 本
\( 3 \) 段目 ・・・ \( 2+5+8=15 \) 本
\( 4 \) 段目 ・・・ \( 2+5+8+11=26 \) 本
\( 5 \) 段目 ・・・ \( 2+5+8+11+14=40 \) 本
\( 6 \) 段目 ・・・ \( 2+5+8+11+14+17=57 \) 本
なので,\( 54 \) 枚のトランプでは,最大 \( 5 \) 段のタワーをつくることができる。
(2) まことさんは,タワーをつくるために,必要なトランプの枚数を効率的に調べる方法について,次のように考えをまとめた。(a),(b)に答えなさい。
【まことさんの考え】
[\( 4 \) 段のとき]
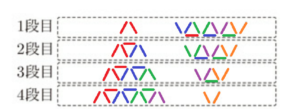
図4のように,\( 4 \) 段のモデルと,同じものを逆さまにしたモデルを組み合わせて,上から \( 1 \) 段目,\( 2 \) 段目,\( 3 \) 段目,\( 4 \) 段目を考えると,各段の棒の本数は,それぞれ ( ウ ) 本で同じになる。
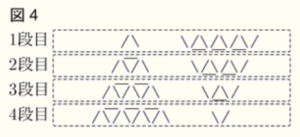
このことを利用すれば,\( 4 \) 段のタワーに必要なトランプの枚数を求めることができる。
[\( n \) 段のとき]
図5のように,\( n \) 段のモデルと,同じものを逆さまにしたモデルを組み合わせて,上から \( 1 \) 段目,\( 2 \) 段目,\( 3 \) 段目,・・・ ,\( n \) 段目を考えると,各段の棒の本数は,それぞれ ( エ ) 本で同じになる。
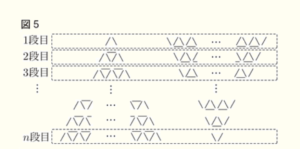
これらの考え方を利用すれば,何段のタワーであっても,必要なトランプの枚数を求めることができる。
(a) 【まことさんの考え】の ( ウ ) にあてはまる数を, エ にはあてはまる \( n \) を用いた式を,それぞれ書きなさい。
【解答】
( ウ ) ・・・ \( 13 \) 本
エ ・・・ \( 3n+1 \) 本
【解説】
( ウ )
すべての段において,横向きの棒は \( 3 \) 本,
斜め向きの棒は,「ハ」の字または「V」の字型を1組と考えると5組ずつあるので,全部で \( 10 \) 本
よって,合計で \( 13 \) 本。
エ
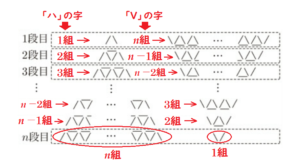
すべての段において,横向きの棒は \( n-1 \) 本,
斜め向きの棒は,「ハ」の字または「V」の字型を1組と考えると
下の図のように \( n+1 \) 組ずつあるので,全部で \( 2(n+1) \) 本
よって,合計で \( (n-1)+2(n+1)=3n+1 \) 本。
(b) \( 20 \) 段のタワーをつくるために,必要なトランプは何枚か,求めなさい。
【解説】
【まことさんの考え】から,
\( n \) 段のとき,各段の棒の本数は,それぞれ \( (3n+1) \) 本で,
これが \( n \) 段あるので,合計の本数は \( n(3n+1) \) 本になります。
これは,タワー2個分の本数なので,タワー1個では,\( \dfrac{n(3n+1)}{2} \) 本になります。
\( 20 \) 段のときの棒の本数は,\( n=20 \) を代入すると,
\( \dfrac{20 \times (3 \times 20+1)}{2}=10 \times 61=610 \) 本
よって,必要なトランプは \( 610 \) 枚。
大問4
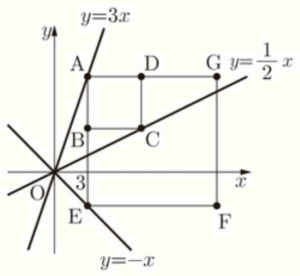
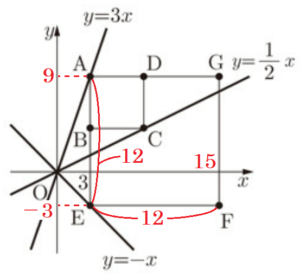
右の図のように,直線 \( y=3x \) 上に点 \( A \),直線 \( y=\dfrac{1}{2}x \) 上に点 \( C \),直線 \( y=-x \) 上に点 \( E \) があり,点 \( A \) の \( x \) 座標は \( 3 \) である。また,四角形 \( ABCD \) と四角形 \( AEFG \) がともに正方形になるように点 \( B,D,F,G \) をとる。ただし,点 \( C \) と点 \( F \) の \( x \) 座標はともに \( 3 \) より大きく,辺 \( AB \) と辺 \( AE \) はともに \( y \) 軸に平行とする。(1)~(4)に答えなさい。
(1) 点 \( E \) の座標を求めなさい。
【解説】
点 \( A \) の \( x \) 座標は \( 3 \) で,辺 \( AE \) はともに \( y \) 軸に平行なので,
点 \( E \) の \( x \) 座標も \( 3 \)
また,\( y=-x \) 上の点なので,\( y \) 座標の値は \( -3 \)
よって,点 \( E \) の座標は \( E(3,-3) \)
(2) 2点 \( A,F \) を通る直線の式を求めなさい。
【解説】
点 \( A \) は \( y=3x \) 上の点で,\( x \) 座標は \( 3 \) なので,
\( y \) 座標の値は \( y=3 \times 3=9 \) であり,
点 \( A \) の座標は \( A(3,9) \)
辺 \( AE \) はともに \( y \) 軸に平行で,
点 \( A \) の \( y \) 座標の値は \( 9 \)
点 \( E \) の \( y \) 座標の値は \( -3 \)
なので,辺 \( AE \) の長さは \( 9-(-3)=12 \)
四角形 \( AEFG \) は正方形なので,
\( EF=AE=12 \)
点 \( F \) の \( x \) 座標は \( 3+12=15 \)
\( AE⊥EF \) より,辺 \( EF \) は \( x \) 軸に平行なので,
\( y \) 座標の値は \( -3 \)
であり,点 \( F \) の座標は \( F(15,-3) \)
求める直線は \( A(3,9),F(15,-3) \) を通るので,
傾き \( =\dfrac{-3-9}{15-3}=-1 \)
この直線の式を \( y=-x+b \) とし,\( x=3,y=9 \) を代入すると,
\( 9=-3+b \)
\( b=12 \)
よって,2点 \( A,F \) を通る直線の式は \( y=-x+12 \)
(3) 正方形 \( ABCD \) を,辺 \( AB \) を回転の軸として1回転させてできる立体の体積を求めなさい。ただし,円周率は \( \pi{} \) とする。
【解説】
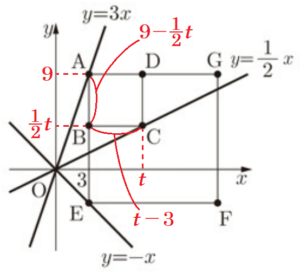
点 \( C \) の \( x \) 座標の値を \( t \) とすると,
点 \( C \) の座標は \( C \left(t,\dfrac{1}{2}t \right) \)
正方形 \( ABCD \) は,辺 \( AB \) が \( y \) 軸に平行,
辺 \( BC \) が \( x \) 軸に平行なので,
点 \( B \) の座標は \( B \left(3,\dfrac{1}{2}t \right) \)
正方形のすべての辺は等しいので,
\( AB=BC \)
\( 9-\dfrac{1}{2}t=t-3 \)
\( \dfrac{3}{2}t=12 \)
\( t=8 \)
よって,点 \( C \) の座標は \( C(8,4) \)
以上より,正方形 \( ABCD \) は1辺の長さが \( 5 \) なので,
求める立体は底面の半径 \( 5 \),高さ \( 5 \) の円柱になります。
この円柱の体積は,
\( (\pi{} \times 5^2) \times 5=125\pi{} \)
(4) 辺 \( FG \) 上に点 \( P \) をとり,\( △OAP \) の周の長さが最小となるような点 \( P \) の座標を求めなさい。
【解説】
\( △OAP \) の周の長さは \( OP+PA+AO \) と表すことができ,
点 \( P \) がどこにあっても,辺 \( AO \) の長さは変わらないので,
\( OP+PA \) が最小のとき,\( △OAP \) の周の長さが最小になります。
線分 \( FG \) について点 \( A \) と対称な点を \( A’ \) とすると,
\( PA=PA’ \) なので,\( OP+PA’=OP+PA \) であり,
線分 \( OA’ \) と線分 \( FG \) の交点が点 \( P \) になるとき,
\( OP+PA \) が最小になります。
\( A(3,9),F(15,-3) \) より,点 \( G \) の座標は \( G(15,9) \)
\( A’G=AG \) なので,\( AG=12 \) より,
点 \( A’ \) の座標は \( A’(27,9) \)
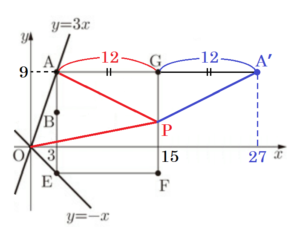
ここから,直線 \( OA’ \) の式は \( y=\dfrac{1}{3}x \)
直線 \( OA’ \) と線分 \( FG \) の交点 \( P \) の \( x \) 座標の値は \( 15 \) なので,
\( y \) 座標の値は
\( y=\dfrac{1}{3} \times 15=5 \)
よって,求める点 \( P \) の座標は,\( P(15,5) \)
大問5
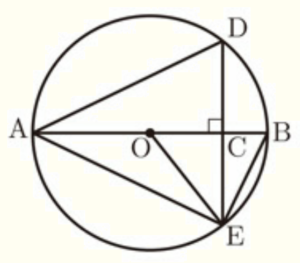
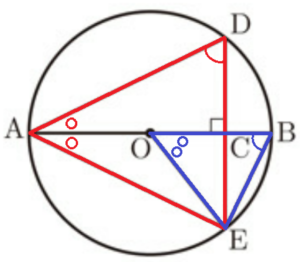
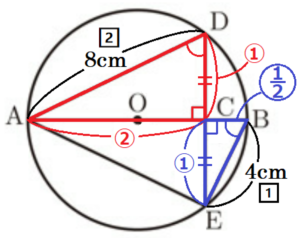
右の図のように,円 \( O \) の直径 \( AB \) 上に点 \( C \) をとり,点 \( C \) を通り直径 \( AB \) に垂直な直線と円 \( O \) との交点をそれぞれ \( D,E \) とする。中心 \( O \) と点 \( E \),点 \( A \) と点 \( D \),点 \( A \) と点 \( E \),点 \( B \) と点 \( E \) をそれぞれ結ぶ。(1)~(4)に答えなさい。
(1) \( ∠AEB \) の大きさを求めなさい。
【解説】
直径に対する円周角なので,\( ∠AEB=90° \)
(2) \( △AED \) ∽ \( △OEB \) の証明について,(a),(b)に答えなさい。
(a) \( △AED \) ∽ \( △OEB \) を証明するために,次のように \( △DAC≡△EAC \) を証明した。
にあてはまる言葉を書きなさい。
【\( △DAC≡△EAC \) の証明】
\( △DAC \) と \( △EAC \) で
\( AC \) は共通だから,\( AC=AC \) ・・・ ①
仮定より, \( ∠DCA=∠ECA=90° \) ・・・ ②
また,直径 \( AB \) は弦 \( DE \) の垂直二等分線だから,
\( DC=EC \) ・・・ ③
➀,②,③ より, が,それぞれ等しいので,\( △DAC≡△EAC \)
(b) (a)で示したことを用いて,\( △AED \) ∽ \( △OEB \) を証明しなさい。
【解答】
\( △AED \) ∽ \( △OEB \) において,
\( △DAC≡△EAC \) より,
\( ∠DAC=∠EAC \) なので,
\( ∠EAD=2∠EAB \) ・・・ ➀
\( ∠EAB \) は弧 \( EB \) に対する円周角,
\( ∠EOB \) は弧 \( EB \) に対する中心角なので,
\( ∠EOB=2∠EAB \) ・・・ ➁
➀➁より,\( ∠EAD=∠EOB \) ・・・ ③
弧 \( AE \) に対する円周角なので,
\( ∠ADE=∠OBE \) ・・・ ➃
③➃より,2組の角がそれぞれ等しいので,
\( △AED \) ∽ \( △OEB \)
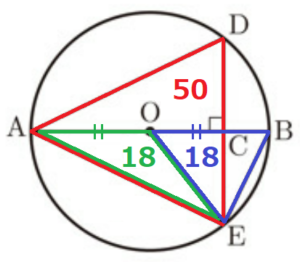
(3) \( △AED \) と \( △OEB \) の相似比が \( 5:3 \) であり,\( △AED \) の面積が \( 50 \; cm^2 \) であるとき,\( △AEB \) の面積を求めなさい。
【解説】
相似な三角形の面積比は相似比の二乗の比になるので,
\( △AED:△OEB=5^2:3^2=25:9 \)
\( 50:△OEB=25:9 \)
\( △OEB=18 \; (cm^2) \)
\( △OEA \) と \( △OEB \) は,
\( OA=OB \),高さが共通なので,
\( △OEA=△OEB=18 \; (cm^2) \)
よって,
\( △AEB=△OEA+△OEB=36 \; (cm^2) \)
(4) \( AD=8 \; cm,BE=4 \; cm \) のとき,\( AC:CB \) を求めなさい。
【解説】
\( △DAC \) と \( △BEC \) において,
\( ∠ADC=∠EBC,∠ACD=∠ECB=90° \) より,
2組の角がそれぞれ等しいので,
\( △DAC \) ∽ \( △BEC \)
対応する辺の比は等しいので,
\( AC:EC=AD:EB=8:4=2:1 \)
\( △DAC≡△EAC \) より,\( DC=EC \) なので,
\( AC:DC=2:1 \)
また,\( DC:BC=2:1 \) でもあるので,
\( AC:DC:BC=2:1:\dfrac{1}{2} \)
よって,
\( AC:BC=2:\dfrac{1}{2}=4:1 \)