大問1
(1) 次の➀~➃を計算せよ。
➀ \( 7-(-6) \)
【解説】
\( =7+6 \)
\( =13 \)
➁ \( 15+(-4)^2 \div (-2) \)
【解説】
\( =15+16 \div (-2) \)
\( =15-8 \)
\( =7 \)
➂ \( (x+2)(x-5)-2(x-1) \)
【解説】
\( =x^2-3x-10-2x+2 \)
\( =x^2-5x-8 \)
➃ \( \sqrt{2} \times \sqrt{6}-\sqrt{27} \)
【解説】
\( =\sqrt{12}-\sqrt{27} \)
\( =2\sqrt{3}-3\sqrt{3} \)
\( =-\sqrt{3} \)
(2) 連立方程式 \( \left\{ \begin{array}{}
x+4y=5 \\
4x+7y=-16 \\
\end{array} \right. \) を解け。
【解説】
\( \left\{ \begin{array}{}
x+4y=5 \;\; ・・・ \;\; ➀ \\
4x+7y=-16 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀\( \times 4- \)➁
\( 9y=36 \)
\( y=4 \)
➀に代入すると,
\( x+4 \times 4=5 \)
\( x=-11 \)
(3) 2次方程式 \( x^2+5x+1=0 \) を解け。
【解答】
\( x=\dfrac{-5±\sqrt{21}}{2} \)
【解説】
\( ax^2+bx+c=0 \) と考えると,\( a=1,b=5,c=1 \) なので,
解の公式より,
\( x=\dfrac{-5±\sqrt{5^2-4 \times 1 \times 1}}{2 \times 1} \)
\( =\dfrac{-5±\sqrt{21}}{2} \)
(4) \( a<0,b<0 \) のとき,\( a+b,a-b,ab,\dfrac{a}{b} \) のうちで,式の値が最も小さいものはどれか。
【解説】
\( a+b \) ・・・ 負の数 \( + \) 負の数 \( = \) 負の数で,\( a+b<a,a+b<b \) になります。
\( a-b \) ・・・ \( a<b \) のとき,\( a-b<0 \) になりますが,\( a-b>a \) になります。
\( a>b \) のとき,\( a-b>0 \) になります。
\( ab \) ・・・ 負の数 \( \times \) 負の数 \( = \) 正の数になります。
\( \dfrac{a}{b} \) ・・・ 負の数 \( \div \) 負の数 \( = \) 正の数になります。
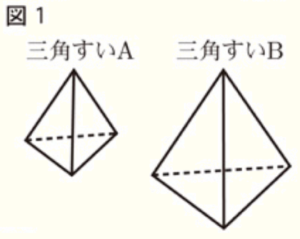
(5) 図1の2つの三角すいA,Bは相似であり,その相似比は \( 2:3 \) である。三角すいAの体積が \( 24 \; cm^3 \) であるとき,三角すいBの体積を求めよ。
【解説】
相似な立体の体積比は相似比の3乗の比と等しくなるので,
\( A:B=2^3:3^3 \)
\( 24:B=8:27 \)
\( B=81 \; (cm^3) \)
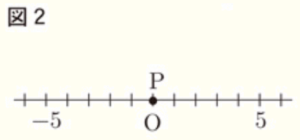
(6) 図2で,数直線上を動く点 \( P \) は,最初,原点 \( O \) にある。点 \( P \) は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に1だけ移動し,裏が出れば負の方向に2だけ移動する。硬貨を3回投げて移動した結果,点 \( P \) が原点 \( O \) にある確率を求めよ。
【解説】
硬貨を3回投げたときの表裏の出方の組み合わせとそれぞれの組み合わせにおける行き先を樹形図として書き,
行き先が原点 \( O \),つまり,\( 0 \) になるところ
赤字 にしてみます。
行き先が原点 \( O \) になる組み合わせは3通り,すべての組み合わせは8通りなので,
求める確率は \( \dfrac{3}{8} \) になります。

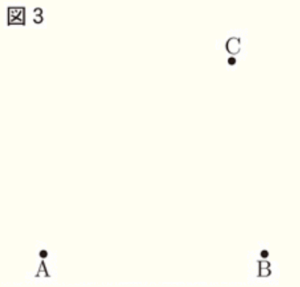
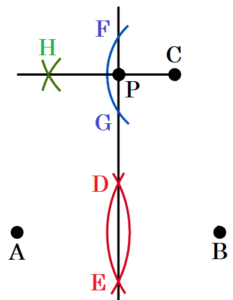
(7) 図3のように,3点 \( A,B,C \) がある。次の条件 ➀,➁ を満たす点 \( P \) を,定規とコンパスを使って解答欄の枠内に作図せよ。なお,作図に使った線は消さずに残しておくこと。
【条件】
➀ \( △PAB \) は,線分 \( AB \) を底辺とする二等辺三角形である。
➁ 直線 \( AB \) と直線 \( PC \) は平行である。
【解答】
手順1 点 \( A,B \) を中心に円弧を描く
(交点を点 \( D,E \) とします)
手順2 2点 \( D,E \) を通る直線を描く
手順3 点 \( C \) を中心に円弧を描く
(直線 \( DE \) との交点を点 \( F,G \) とします)
手順4 点 \( F,G \) を中心に円弧を描く
(交点を点 \( H \) とします)
手順5 2点 \( C,H \) を通る直線を描く
手順3と手順5の直線の交点が求める点 \( P \) になります。
【解説】
条件➀より,点 \( P \) から線分 \( AB \) に垂線をひくと,線分 \( AB \) の垂直二等分線になります。
また,この直線を \( l \) とすると,\( AB⊥l,AB//PC \) より,\( PC⊥l \) になります。
以上より,線分 \( AB \) の垂直二等分線と,この垂直二等分線に点 \( C \) を通る垂線をひいたときの交点が
求める点 \( P \) になります。
(8) A中学校の1年生75人と3年生90人に,通学時間についてアンケートをした。図4は,その結果について,累積相対度数を折れ線グラフに表したものである。例えば,このグラフから,1年生では,通学時間が10分未満の生徒が,1年生全体の42%であることを読み取ることができる。図4から読み取ることができることがらとして適切なものを,次のア~オから全て選び,その記号を書け。
ア 通学時間の中央値は,1年生の方が3年生よりも大きい。
イ 通学時間が20分未満の生徒は,1年生も3年生も半分以上いる。
ウ 通学時間が25分未満の生徒の人数は,1年生も3年生も同じ
である。
エ 通学時間が25分以上30分未満の生徒の人数は,3年生の方が
1年生よりも多い。
オ 全体の傾向としては,1年生の方が3年生よりも通学時間が短い
といえる。
【解説】
ア 中央値は,累積相対度数が \( 0.50 \) のところの階級になります。
1年生は10分以上15分未満,3年生は15分以上20分未満の階級にあるので,正しい。
イ 15分以上20分未満の階級の累積相対度数は,1年生が \( 0.66 \),3年生が \( 0.52 \) で,
どちらも \( 0.50 \) を超えているので,半分以上いるといえます。
ウ 累積相対度数は \( \dfrac{その階級の累積度数}{すべての階級の度数の合計} \) で求めることができます。
1年生と3年生で累積相対度数は同じですが,全体の人数が異なるので,累積度数も異なります。
1年生 ・・・ \( 75 \times 0.76=57 \)(人)
3年生 ・・・ \( 90 \times 0.76=68.4 \)(人)
エ 25分以上30分未満の階級の相対度数は
”30分未満の累積相対度数” \( – \) ”25分未満の累積相対度数” で求めることができるので,
1年生 ・・・ \( 0.80-0.76=0.04 \)
3年生 ・・・ \( 0.90-0.76=0.14 \)
よって,25分以上30分未満の生徒の人数は,
1年生 ・・・ \( 75 \times 0.04=3 \)(人)
3年生 ・・・ \( 90 \times 0.14=12.6 \)(人)
オ 横軸が通学時間なので,折れ線が左にある方が通学時間が短い傾向にあるといえます。
図4では,25分未満の範囲では明らかに1年生の折れ線が左側にあり,25分以上はほぼ同じと
みることができます。
よって,1年生の方が3年生よりも通学時間が短いといえます。
大問2
太郎さんと花子さんは,ロボット掃除機が部屋を走行する様子を見て,動く図形について興味をもった。次の 内は,いろいろな図形の内部を円や正方形が動くとき,円や正方形が通過する部分について考えている,太郎さんと花子さんの会話である。
花子:長方形の内部を円や正方形が動くとき,正方形は,長方形の内部をくまなく通過できるね。
でも,円は,長方形の内部で通過できないところがあるよ。
正方形は,どんな図形の内部でもくまなく通過できるのかな。
太郎:どうかな。三角形の内部では,円も正方形も通過できないところがあるよ。
いろいろな図形の内部を円や正方形が動く場合,通過できるところに違いがあるね。
花子:直角二等辺三角形の内部を円や正方形が動くときについて,真上から見た図をかいて考えて
みよう。
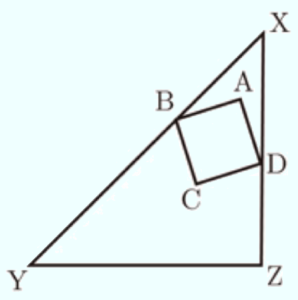
\( XZ=YZ,∠XZY=90° \) の直角二等辺三角形 \( XYZ \) の内部を,円 \( O \),正方形 \( ABCD \) が動くとき,各問いに答えよ。ただし,円周率は \( \pi{} \) とする。
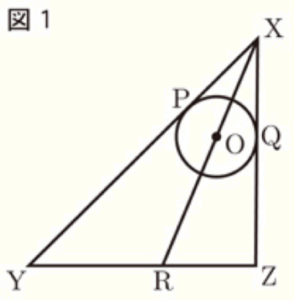
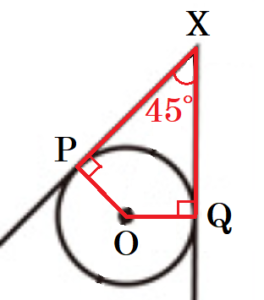
(1) 図1で,円 \( O \) は辺 \( XY,XZ \) に接しており,2点 \( P,Q \) はその接点である。また,点 \( R \) は直線 \( XO \) と辺 \( YZ \) との交点である。➀〜➂の問いに答えよ。
➀ \( ∠POQ \) の大きさを求めよ。
【解説】
四角形 \( XPOQ\) において,
\( △XYZ \) は直角二等辺三角形なので,\( ∠PXQ=45° \)
線分 \( XY,XZ \) はどちらも円 \( O \) の接線なので,
\( ∠OPX=∠OQX=90° \)
よって,
\( ∠POQ=360°-(∠PXQ+∠OPX+∠OQX) \)
\( =360°-(45°+90°+90°) \)
\( =135° \)
➁ 線分 \( XR \) 上にある点はどのような点か。「辺」と「距離」の語を用いて簡潔に説明せよ。
【解答】
辺 \( XY,XZ \) との距離が等しくなる点
【解説】
2本の接線の交点と円の中心を通る直線は,2本の接線によってできる角の二等分線になります。
(今回でいうと,\( ∠PXO=∠QXO \) になります。)
線分 \( XR \) 上に点 \( A \) をとり,辺 \( XY,XZ \) に垂線をひいたときの交点を点 \( B,C \) とすると,
\( ∠ABX=∠ACX=90°,∠BXA=∠CXA \),\( AX \) は共通
なので,\( △ABX≡△ACX \) であり,\( AB=AC \) になっています。
よって,点 \( A \) と辺 \( XY,XZ \) との距離は等しくなります。
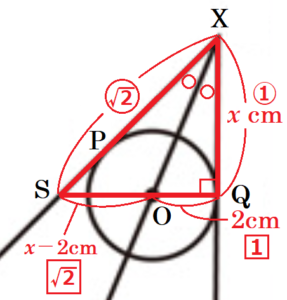
➂ 円 \( O \) の半径が \( 2 \; cm \) であるとき,線分 \( XP \) の長さを求めよ。
【解答】
\( 2+2\sqrt{2} \; cm \)
【解説】
同じ点からひいた2本の接線の長さは等しく,\( XP=XQ \) なので,線分 \( XQ \) の長さを求めます。
線分 \( OQ \) の延長線と線分 \( XY \) の交点を点 \( S \) とすると,
\( ∠SXQ=45°,∠OQX=90° \) より,
\( △SQX \) は直角二等辺三角形になっています。
ここから,\( XQ=x \; cm \) とすると,\( QS=XQ=x \; cm \)
また,\( XS:XQ=\sqrt{2}:1 \)
線分 \( XO \) は \( ∠SXQ=45° \) の二等分線なので,
\( SO:OQ=XS:XQ=\sqrt{2}:1 \) になります。
\( QS=x \; cm,OQ=2 \; cm \) より,\( SO=x-2 \; cm \) なので,
\( SO:OQ=\sqrt{2}:1 \)
\( x-2:2=\sqrt{2}:1 \)
\( x-2=2\sqrt{2} \)
\( x=2+2\sqrt{2} \; (cm) \)
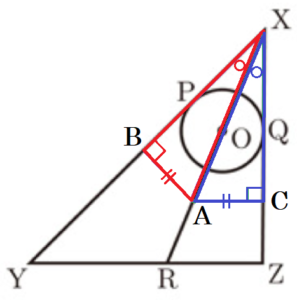
(2) 次の 内は,\( △XYZ \) の内部を,正方形 \( ABCD \) が働く場合について考えている,太郎さんと花子さんの会話である。➀,➁の問いに答えよ。
花子:図2のように,正方形 \( ABCD \) が,点 \( X \) に最も
近づくように,正方形 \( ABCD \) の2点 \( B,D \) が
それぞれ辺 \( XY,XZ \) 上にある図をかいたよ。
太郎:図2の正方形 \( ABCD \) で,点 \( X \) に最も近いのは,
点 \( A \) だね。
花子:そうだね。2点 \( X,A \) 間の距離はどのくらいの長さに
なっているのかな。図2からわかることは何だろう。
太郎:点 \( A \) を中心として2点 \( B,D \) を通る円をかくと,
点 \( X \) も円 \( A \) の周上にありそうだね。
花子:円 \( A \) で,弧 \( BD \) に対する中心角は \( ∠BAD \) に
なるね。\( ∠BAD=90° \) で,\( ∠BXD=45° \) だから,
\( ∠BXD \) は弧 \( BD \) に対する円周角になっているね。
点 \( X \) は円 \( A \) の周上にあるといえるよ。
太郎:2点 \( X,A \) 間の距離は あ と等しいといえるね。
花子:正方形 \( ABCD \) が動いて,辺 \( XY,XZ \) 上の
2点 \( B,D \) の位置が変わっても,2点 \( X,A \) 間の
距離について同じことがいえるから,
正方形 \( ABCD \) が,\( △XYZ \) の内部をくまなく動くとき,
正方形 \( ABCD \) が通過した部分の面積もわかるね。
➀ あ に当てはまる語句を,次のア~エから1つ選び,その記号を書け。
ア 正方形 \( ABCD \) の対角線の長さ イ 正方形 \( ABCD \) の1辺の長さ
ウ 正方形 \( ABCD \) の対角線の長さの半分 エ 正方形 \( ABCD \) の1辺の長さの半分
【解説】
3点 \( A,B,D \) はいずれも円 \( A \) の周上の点なので,\( AX=AB=AD \) になっています。
\( AB,AD \) は,正方形 \( ABCD \) の辺なので,
\( AX \) は正方形 \( ABCD \) の1辺の長さと等しくなっています。
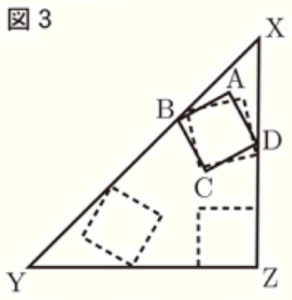
➁ 図3のように,正方形 \( ABCD \) が,\( △XYZ \) の内部をくまなく動くとき,正方形 \( ABCD \) が通過した部分の面積を求めよ。ただし,\( XZ=10 \; cm,AB=3 \; cm \) とする。
【解答】
\( 50-\dfrac{9}{4}\pi{} \; cm^2 \)
【解説】
点 \( A \) が辺 \( XZ \) 上にあるとき,正方形 \( ABCD \) を点 \( X \) に一番近くなるところまで移動させると,\( AX=3cm \) になります。
(\( △XAB \) が直角二等辺三角形になるため)
同様に,点 \( A \) が辺 \( XY \) 上にあるときも,\( AX=3cm \) のときに
点 \( X \) に一番近くなります。
また,点 \( A \) が \( △XYZ \) の内部にあるときも,
会話の内容と問➀から \( AX=3cm \) となります。
以上より,点 \( A \) が辺 \( XY \) から辺 \( XZ \) まで移動するときは,
常に点 \( X \) からの距離が \( 3cm \) になり,
正方形が通過しない部分の形状は,
半径 \( 3cm \),中心角 \( 45° \) のおうぎ形になります。
これは,点 \( Y \) 付近についても同様のことがいえます。
よって,正方形 \( ABCD \) が通過した部分の面積は,
\( △XYZ \) から半径 \( 3cm \),中心角 \( 45° \) のおうぎ形2つ分を
除いたものになるので,
\( \left( 10 \times 10 \times \dfrac{1}{2} \right)-\left( \pi{} \times 3^2 \times \dfrac{45°}{360°} \times 2 \right)=50-\dfrac{9}{4}\pi{} \; (cm^2) \)
大問3
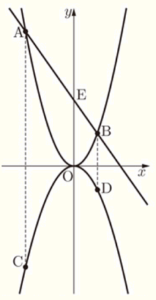
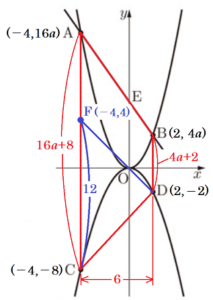
右の図のように,関数 \( y=ax^2 \; (a>0) \) のグラフ上に,2点 \( A,B \) があり,関数 \( y=-\dfrac{1}{2}x^2 \) のグラフ上に,2点 \( C,D \) がある。2点 \( A,C \) の \( x \) 座標は \( -4 \) であり,2点 \( B,D \) の \( x \) 座標は \( 2 \) である。2点 \( A,B \) を通る直線と \( y \) 軸との交点を \( E \) とする。原点を \( O \) として,各問いに答えよ。
(1) 関数 \( y=-\dfrac{1}{2}x^2 \) について,\( x \) の変域が \( -4≦x≦2 \) のときの \( y \) の変域を求めよ。
【解説】
\( y=-\dfrac{1}{2}x^2 \) は \( x^2 \) の係数が \( -\dfrac{1}{2} \) で負の値なので,
\( x \) の変域が \( 0 \) を含んでいることから,
\( y \) の最大値は \( 0 \) になります。
また,\( y \) の最小値は,
\( x \) の値の絶対値が最も大きくなる時の値
になります。
\( -4≦x≦2 \) より,\( x \) の値の絶対値が最も大きくなるのは
\( x=-4 \) のときなので,
\( y=-\dfrac{1}{2} \times (-4)^2=-8 \)
以上より,\( x \) の変域が \( -4≦x≦2 \) のときの
\( y \) の変域は,\( -8≦y≦0 \)

(2) 2点 \( C,D \) を通る直線の式を求めよ。
【解説】
点 \( D \) の \( x \) 座標は \( 2 \) なので,
\( y \) 座標の値は,
\( y=-\dfrac{1}{2} \times 2^2=-2 \)
よって,求める直線は,\( C(-4,-8),D(2,-2) \) を通るので,
傾き \( =\dfrac{-2-(-8)}{2-(-4)}=1 \)
求める直線の式を \( y=x+b \) とし,\( x=2,y=-2 \) を代入すると,
\( -2=2+b \)
\( b=-4 \)
以上より,求める直線の式は \( y=x-4 \)
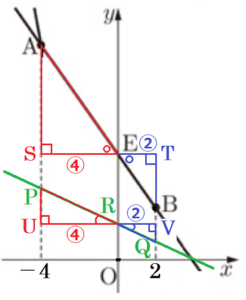
(3) \( a \) の値が大きくなるとき,それにともなって小さくなるものを,次のア~エから1つ選び,その記号を書け。
ア 直線 \( AB \) の傾き
イ 線分 \( AB \) の長さ
ウ \( △OAB \) の面積
エ \( AE:EB \) の比の値
【解説】
関数 \( y=cx^2 \; (a>c>0) \) のグラフを書き足してみます。
ア 直線 \( AB \) と直線 \( PQ \) では,直線 \( AB \) の方が
傾きが小さくなっています。
つまり,\( a \) の値が大きくなるとき,傾きは小さくなります。
(傾きは負の値のとき,急角度の方が傾きが小さくなります。)
イ \( AB=\sqrt{AM^2+BM^2},PQ=\sqrt{QN^2+PN^2} \) なので,
\( AM=QN=6,BM>PN \) より,
\( AB=\sqrt{36+BM^2} \)
\( PQ=\sqrt{36+PN^2} \)
となり,\( AB>PQ \)
つまり,\( a \) の値が大きくなるとき,
線分 \( AB \) の長さは長くなります。
ウ \( △OAB=OE \times 4 \times \dfrac{1}{2}+OE \times 2 \times \dfrac{1}{2} \)
\( =OE \times (4+2) \times \dfrac{1}{2} \)
\( =OE \times 6 \times \dfrac{1}{2} \)
\( △OPQ=OR \times 4 \times \dfrac{1}{2}+OR \times 2 \times \dfrac{1}{2} \)
\( =OR \times (4+2) \times \dfrac{1}{2} \)
\( =OR \times 6 \times \dfrac{1}{2} \)
となります。
\( OE>OR \) なので,\( △OAB>△OPQ \)
つまり,\( a \) の値が大きくなるとき,
\( △OAB \) の面積は大きくなります。
エ \( △ASE \)∽\( △BTE \) で,\( SE:TE=4:2=2:1 \) なので,
\( AE:EB=2:1 \)
\( △PUR \)∽\( △QVR \) で,\( UR:QR=4:2=2:1 \) なので,
\( PR:RQ=2:1 \)
つまり,\( a \) の値が大きくなっても,
\( AE:EB \) の比の値は変わりません。
(4) 直線 \( OD \) が四角形 \( ACDB \) の面積を2等分するとき,\( a \) の値を求めよ。
【解答】
\( a=\dfrac{7}{10} \)
【解説】
\( A(-4,16a),B(2,4a),C(-4,-8),D(2,-2) \) なので,
四角形 \( ACDB \) は,
上底 \( 4a+2 \),下底 \( 16a+8 \),高さ \( 6 \) の台形
になっています。
四角形 \( ACDB \) の面積は,
四角形 \( ACDB=\{ (4a+2)+(16a+8) \} \times 6 \times \dfrac{1}{2} \)
\( =60a+30 \)
直線 \( OD \) は原点 \( O \) と \( D(2,-2) \) を通るので,
直線 \( OD \) の式は,\( y=-x \) となります。
直線 \( OD \) と線分 \( AC \) の交点を \( F \) とすると,\( F(-4,4) \) なので,
\( △CDF=12 \times 6 \times \dfrac{1}{2}=36 \)
\( △CDF \) の面積が四角形 \( ACDB \) の面積の半分になるとき,
\( \dfrac{1}{2} \) 四角形 \( ACDB=△CDF \)
\( \dfrac{1}{2} \times (60a+30)=36 \)
\( 60a+30=72 \)
\( 60a=42 \)
\( a=\dfrac{7}{10} \)
大問4
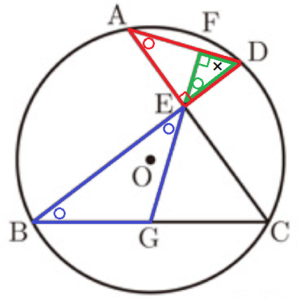
右の図で,4点 \( A,B,C,D \) は円 \( O \) の周上にある。点 \( E \) は線分 \( AC \) と線分 \( BD \) との交点で \( AC⊥BD \) であり,点 \( F \) は線分 \( AD \) 上の点で \( EF⊥AD \) である。点 \( G \) は直線 \( EF \) と線分 \( BC \) との交点である。各問いに答えよ。
(1) \( △AEF \) ∽ \( △BCE \) を証明せよ。
【解答】
\( △AEF \) と \( △BCE \) において,
弧 \( CD \) に対する円周角なので,\( ∠EAF=∠CBE \) ・・・ ①
\( EF⊥AD \) なので,\( ∠EFA=90° \) ・・・ ➁
\( AC⊥BD \) なので,\( ∠CEB=90° \) ・・・ ➂
➁➂より,\( ∠EFA=∠CEB=90° \) ・・・ ➃
①➃より,2組の角がそれぞれ等しいので,
\( △AEF \) ∽ \( △BCE \)
(2) \( ∠DAE=a° \) とするとき,\( ∠BGE \) の大きさを \( a \) を用いて表せ。
【解説】
\( △AED \) は,直角三角形になっているので,
\( ∠DAE= \) ○,\( ∠ADE= \) × とすると,
○ \( + \) × \( +90°=180° \)
○ \( + \) × \( =90° \)
\( △DEF \) も直角三角形になっているので,
\( ∠DEF=180°-(90°+ \) ×\( ) \)
\( =90°- \) ×
\( = \) ○
よって,\( ∠DAE=∠DEF= \) ○ ・・・ ①
対頂角は等しいので,\( ∠GEB=∠DEF= \) ○ ・・・ ➁
弧 \( CD \) に対する円周角なので,\( ∠DAE=∠GBE= \) ○ ・・・ ➂
①➁➂より,\( ∠GEB=∠GBE- \) ○
以上より,\( ∠DAE=∠GEB=∠GBE=a° \) なので,
\( ∠BGE=180°-2a° \)
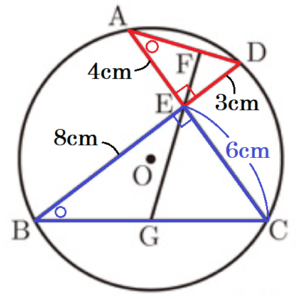
(3) \( DE=3 \; cm,AE=4 \; cm,BE=8 \; cm \) のとき,➀,➁の問いに答えよ。
➀ \( △CEG \) の面積を求めよ。
【解説】
\( ∠AED=∠BEC=90°,∠DAE=∠CBE \) より,
\( △AED \) ∽ \( △BEC \) なので,
\( AE:DE=BE:CE \)
\( 4:3=8:CE \)
\( CE=6 \; (cm) \)
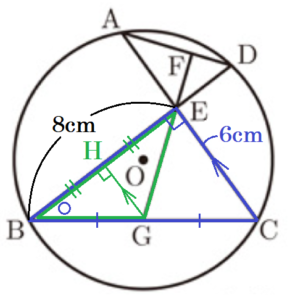
点 \( G \) から線分 \( BE \) に垂線をひき,交点を点 \( H \) とすると,
(2) より,\( △BGE \) は二等辺三角形なので,
点 \( H \) は線分 \( BE \) の中点になっています。
さらに,\( △BHG \) ∽ \( △BEC \) なので,
\( BH=HE \) より,\( BG=GC \) になっています。
\( △BEC \) と \( △CEG \) は高さが共通なので,
面積比は底辺の長さの比になります。
\( △BEC \) の面積は,
\( △BEC=BE \times CE \times \dfrac{1}{2} \)
\( =8 \times 6 \times \dfrac{1}{2} \)
\( =24 \; (cm^2) \)
なので,
\( △BEC:△CEG=BC:GC \)
\( 24:△CEG=2:1 \)
\( △CEG=12 \; (cm^2) \)
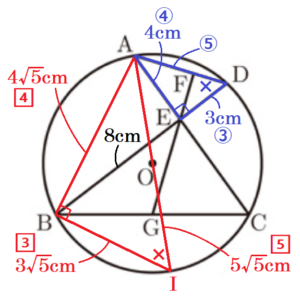
➁ 円 \( O \) の半径を求めよ。
【解答】
\( \dfrac{5\sqrt{5}}{2} \; cm \)
【解説】
2点 \( A,O \) をを通る直線と円 \( O \) の交点のうち,
点 \( A \) と異なる点を点 \( I \) とします。
また,補助線 \( AB \) をひくと,
\( ∠ABI=∠AED=90°,∠AIB=∠ADE \) より,
\( △AED \) ∽ \( △ABI \)
\( △ABE \) において,三平方の定理より,
\( AB^2=AE^2+BE^2 \)
\( =4^2+8^2 \)
\( =80 \)
\( AB=4\sqrt{5} \; (cm) \)(\( AB>0 \)より)
また,\( △AED \) において,\( DE=3 \; cm,AE=4 \; cm \) より \( AE:AD=4:5 \) になるので,
\( △ABI \) において,\( AB:AI=4:5 \) であり,
\( AB:AI=4:5 \)
\( 4\sqrt{5}:AI=4:5 \)
\( AI=5\sqrt{5} \; (cm) \)
線分 \( AI \) は円 \( O \) の直径なので,半径 \( AO \) は,
\( AO=\dfrac{1}{2}AI=\dfrac{5\sqrt{5}}{2} \; (cm) \)