大問1
(1) \( -2+5-1 \) を計算しなさい。
(2) \( 6 \left( \dfrac{3}{2}x-1 \right) \) を計算しなさい。
【解説】
\( =6 \times \dfrac{3}{2}x-6 \times 1 \)
\( =9x-6 \)
(3) \( 4\sqrt{2} \times 2\sqrt{3} \) を計算しなさい。
(4) \( x^2+8x+16 \) を因数分解しなさい。
(5) 2次方程式 \( x^2-3x-5=0 \) を解きなさい。
【解答】
\( \dfrac{3±\sqrt{29}}{2} \)
【解説】
この方程式を \( ax^2+bx+c=0 \) と考えると,\( a=1,b=-3,c=-5 \) なので,
解の公式より,
\( x=\dfrac{-(-3)±\sqrt{(-3)^2-4 \times 1 \times (-5)}}{2 \times 1} \)
\( =\dfrac{3±\sqrt{29}}{2} \)
大問2
貯金箱をあけたところ,\( 10 \) 円硬貨が \( a \) 枚,\( 1 \) 円硬貨が \( b \) 枚入っており,合計金額は \( 500 \) 円以上でした。
このときの数量の間の関係を,不等式で表しなさい。
大問3
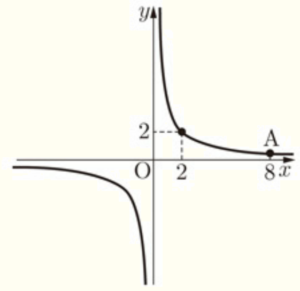
右の図は反比例のグラで,点 \( (2,2) \) を通ります。このグラフ上で,\( x \) 座標が \( 8 \) である点 \( A \) の \( y \) 座標を求めなさい。
【解説】
反比例を表す式は \( y=\dfrac{a}{x} \) なので,\( x=2,y=2 \) を代入すると,
\( 2=\dfrac{a}{2} \)
\( a=4 \)
よって,\( y=\dfrac{4}{x} \) に \( x=8 \) を代入すると,
\( y=\dfrac{4}{8}=\dfrac{1}{2} \)
大問4
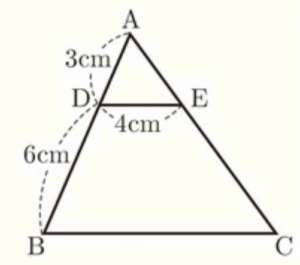
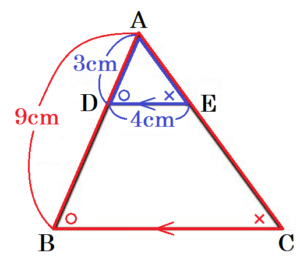
(1) 右の図で,\( BC//DE \) であるとき,線分 \( BC \) の長さを求めなさい。
【解説】
\( BC//DE \) より,同位角は等しいので,
\( ∠ABC=∠ADE,∠ACB=∠AED \)
2組の角がそれぞれ等しいので,
\( △ABC \) ∽ \( △ADE \)
対応する辺の比は等しいので,
\( AB:AD=BC:DE \)
\( 9:3=BC:4 \)
\( BC=12 \; (cm) \)
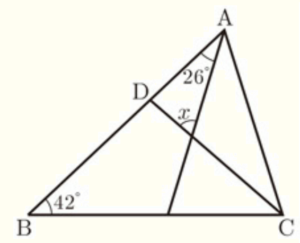
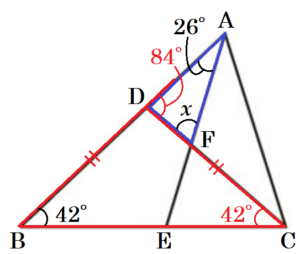
(2) 右の図で,\( BD=CD \) であるとき,\( ∠x \) の大きさを求めなさい。
【解説】
右の図のように2点 \( E,F \) とすると,
\( BD=CD \) より,
\( ∠DCB=∠DBC=42° \)
\( △BCD \) の外角なので,
\( ∠ADF=42°+42°=84° \)
\( △ADF \) において,
\( ∠x=180°-(84°+26°)=70° \)
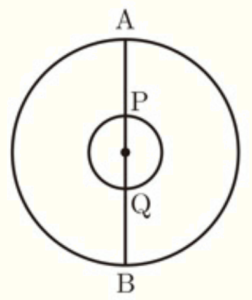
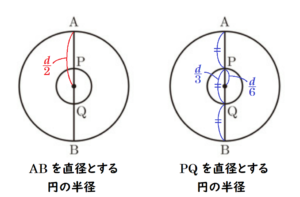
(3) 右の図のように,線分 \( AB \) を3等分する2点 \( P,Q \) をとります。線分 \( AB \) の中点を中心とし,\( AB \) を直径とする円と \( PQ \) を直径とする円をかきます。
このとき,\( AB \) を直径とする円の面積は,\( PQ \) を直径とする円の面積の何倍か求めなさい。
【解説】
\( AB \) を直径とする円と \( PQ \) を直径とする円は相似な図形になっています。
2点 \( P,Q \) が線分 \( AB \) を3等分する点であることから,
相似比は,\( AB:PA=3:1 \) なので,
\( AB \) を直径とする円の面積を \( S_1 \),\( PQ \) を直径とする円 の面積を \( S_2 \) とすると,
面積比は,\( S_1:S_2=3^2:1^2=9:1 \)
よって,
\( AB \) を直径とする円の面積は,\( PQ \) を直径とする円の面積の \( 9 \) 倍になります。
【別解】
線分 \( AB \) の長さを \( d \) とすると,
\( AB \) を直径とする円の半径は \( \dfrac{d}{2} \) と表すことができるので,
面積 \( S_1 \) は,
\( S_1=\pi{} \times \left( \dfrac{d}{2} \right)^2=\dfrac{\pi{}}{4}d^2 \)
2点 \( P,Q \) は,線分 \( AB \) を3等分する点なので,
\( PQ \) の長さは \( \dfrac{d}{3} \) と表すことができます。
ここから,\( PQ \) を直径とする円の半径は \( \dfrac{d}{6} \) と表すことができるので,
面積は \( S_2 \) は,
\( S_2=\pi{} \times \left( \dfrac{d}{6} \right)^2=\dfrac{\pi{}}{36}d^2 \)
よって,
\( S_1:S_2=\dfrac{\pi{}}{4}d^2:\dfrac{\pi{}}{36}d^2 \)
\( =\dfrac{1}{4}:\dfrac{1}{36} \)
\( =9:1 \)
より,
\( AB \) を直径とする円の面積は,\( PQ \) を直径とする円の面積の \( 9 \) 倍
大問5
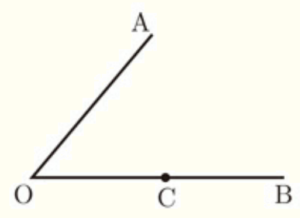
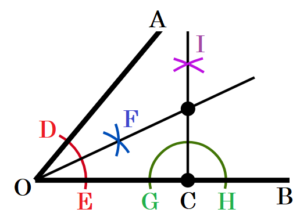
右の図で,\( ∠AOB \) の辺 \( OB \) 上の点 \( C \) で辺 \( OB \) に接し,辺 \( OA \) にも接する円の中心を作図によって求め,\( \bullet \) 印で示しなさい。
ただし,作図には定規とコンパスを用い,作図に使った線は消さないでおくこと。
【解答】
手順1 点 \( O \) を中心に円弧を描く。
(線分 \( OA,OB \) との交点をそれぞれ点 \( D,E \) とします。)
手順2 点 \( D,E \) を中心に円弧を描く。
(交点をそれぞれ点 \( F \) とします。)
手順3 2点 \( O,F \) を通る直線を描く。
手順4 点 \( C \) を中心に円弧を描く。
(線分 \( OB \) との交点をそれぞれ点 \( G,H \) とします。)
手順5 点 \( G,H \) を中心に円弧を描く。
(交点をそれぞれ点 \( I \) とします。)
手順6 2点 \( C,I \) を通る直線を描く。
手順3と手順6の交点が求める点になります。
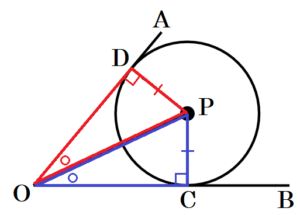
【解説】
円と接線の関係について,以下の性質があります。
・ 円の半径と接線は接点において垂直に交わる
・ 円の中心と2本の接線の交点を結ぶ直線は,2本の接線がなす角の二等分線になる。
ここから,
「点 \( C \) を通り,線分 \( OB \) に垂直な直線」と「\( ∠AOB \) の二等分線」の交点が
求める点になります。
円の中心と2本の接線の交点を結ぶ直線が,2本の接線がなす角の二等分線になる理由
円 \( P \) と 線分 \( OA,OB \) との接点を
それぞれ,\( D,C \) とすると,
\( △OPD \) と \( △OPC \) において,
円の半径と接線は接点において垂直に交わるので,
\( △ODP=△OCP=90° \) ・・・ ➀
円の半径なので,
\( PD=PC \) ・・・ ➁
また,\( OP \) は共通 ・・・ ③
➀➁③より,
直角三角形の斜辺と他の1辺がそれぞれ等しいので,
\( △OPD≡△OPC \)
対応する角は等しいので,
\( △POD=△POC \)
よって,直線 \( OP \) は,\( ∠AOB \) の二等分線になります。
大問6
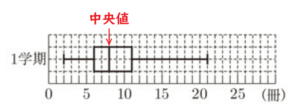
図書委員のしおりさんは,クラスの生徒 \( 10 \) 人について,1学期に読んだ本の冊数を調べました。
次の図は,その分布のようすを箱ひげ図に表したものです。
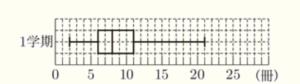
このとき,次の(1),(2)の問いに答えなさい。
(1) 1学期に読んだ本の冊数の中央値を求めなさい。
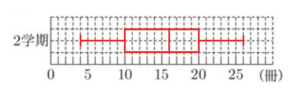
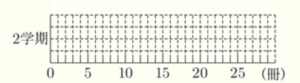
(2) 図書委員会では,2学期に読む本の冊数を増やす取り組みをしました。
次のデータは,\( 10 \) 人が2学期に読んだ本の冊数を調べ,少ないほうから順に整理したものです。
\( \fbox{4 8 10 13 15 17 18 20 22 26 (単位 冊)} \)
このとき,2学期に読んだ本の冊数の箱ひげ図をかきなさい。
【解説】
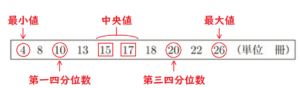
全体のデータ数が \( 10 \) 個なので,
第一四分位数 ・・・ \( 10 \) 冊(値の小さい方から3番目の値)
中央値 ・・・ \( 16 \) 冊(値の小さい方から5番目の値と6番目の値の平均値)
第三四分位数 ・・・ \( 20 \) 冊(値の小さい方から8番目の値)
になります。
大問7
あおいさんとひなたさんは,何も書かれていないカードを4枚ずつ持っています。2人は,自分が持っている4枚のカードに,正の整数を1つずつ,和が \( 10 \) になるように書き,次のルールにしたがってゲームをします。
ルール
① 数が見えない状態で,4枚のカードをよくきって並べて置く。
② 自分の4枚のカードから1枚だけを選ぶ。
③ ②で選んだカードに書かれた数を比べて,数が大きい方を勝ちとする。同じ数の場合は引き分けと
する。
このとき,次の(1),(2)の問いに答えなさい。
ただし,どのカードを選ぶことも同様に確からしいものとします。
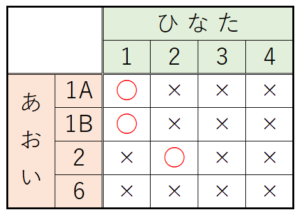
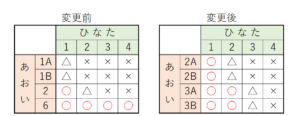
(1) あおいさんとひなたさんは,4枚のカードに次のように数を書いて,ゲームを1回しました。

このとき,引き分けになる確率を求めなさい。
【解説】
あおいさんが持っている2枚の \( 1 \) のカードに
\( 1A,1B \) と名前をつけて,
あおいさんとひなたさんが選ぶカードの組み合わせを
表に書き出し,引き分けになるところに ○ ,
それ以外のところに × をつけます。
引き分けになる組み合わせは3通り,
すべての組み合わせは16通りなので,
求める確率は,\( \dfrac{3}{16} \)
(2) 2人は,もう一度,カードに書く数を考えて,ゲームを1回することにしました。あおいさんは,次のように数を変更し,ひなたさんは,はじめに書いたカードの数を変更しませんでした。

このとき,あおいさんが勝つ確率は,数を変更する前に比べて,大きくなりますか,小さくなります
か,変わらないですか。また,その理由を確率を用いて説明しなさい。
【解答】
大きくなる
変更前のあおいさんが勝つ確率は,\( \dfrac{5}{16} \)
変更後のあおいさんが勝つ確率は,\( \dfrac{3}{8} \)
で,変更後のあおいさんが勝つ確率の方が大きいため。
【解説】
あおいさんが数を変更する前と後の両方について,
あおいさんとひなたさんが選ぶカードの組み合わせとそのときの勝ち負けを表に書き出し,
あおいさんの勝ちになるところに
○ ,引き分けになるところに
△ ,負けになるところに × をつけます。
数を変更する前は,
あおいさんの勝ちになる組み合わせは5通り,すべての組み合わせは16通りなので,
求める確率は,\( \dfrac{5}{16} \)
数を変更した後は,
あおいさんの勝ちになる組み合わせは6通り,すべての組み合わせは16通りなので,
求める確率は,\( \dfrac{6}{16}=\dfrac{3}{8} \)
大問8
あるお店で,スケッチブック1冊と色えんぴつ1セットを買いました。定価の合計は \( 1450 \) 円でしたが,その日はスケッチブックが定価の \( 70 \% \) で,色えんぴつが定価の \( 80 \% \) で売られていたので,代金の合計は \( 1080 \) 円でした。
このとき,スケッチブック1冊と色えんぴつ1セットの定価をそれぞれ求めなさい。
ただし,用いる文字が何を表すかを示して方程式をつくり,それを解く過程も書くこと。
なお,消費税は考えないものとします。
【解答】
スケッチブック1冊の定価を \( x \) 円,と色えんぴつ1セットの定価を \( y \) 円とすると,
\( \left\{ \begin{array}{}
x+y=1450 \;\; ・・・ \;\; ➀ \\
\dfrac{70}{100}x+\dfrac{80}{100}y=1080 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( \times 8 \;\; – \) ➁ \( \times 10 \)
\( x=800 \)
➀に代入すると,
\( 800+y=1450 \)
\( y=650 \)
よって,
スケッチブック1冊の定価は \( 800 \) 円
色えんぴつ1セットの定価は \( 650 \) 円
大問9
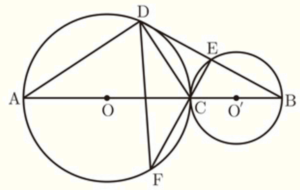
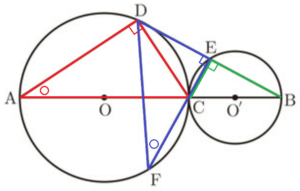
下の図のように,線分 \( AB \) 上に点 \( C \) をとり,線分 \( AC,BC \) を直径とする円をそれぞれ \( O,O’ \) とします。点 \( D \) は円 \( O \) の周上にあり,線分 \( DB \) と円 \( O’ \) との交点を \( E \) とします。また,直線 \( EC \) と円 \( O \) との交点を \( F \) とします。
ただし,点 \( D \) は2点 \( A,C \) と異なる点とします。
このとき,\( △ADC \) ∽ \( △FED \) であることを証明しなさい。
【解答】
\( △ADC \) と \( △FED \) において,
直径に対する円周角なので,
\( ∠ADC=∠CEB=90° \) ・・・ ➀
\( ∠CEB=90° \) より,\( FE⊥BD \) なので,
\( ∠FED=∠CEB=90° \) ・・・ ➁
➀➁より,
\( ∠ADC=∠FED \) ・・・ ③
弧 \( CD \) に対する円周角なので,
\( ∠CAD=∠DFE \) ・・・ ➃
③➃より,2組の角がそれぞれ等しいので,
\( △ADC \) ∽ \( △FED \)
大問10
自宅で加湿器を使用しているさつきさんは,加湿器を使うとタンクの水がどのように減っていくのか疑問に思いました。
その加湿器は,「強」 または 「弱」の設定で使用できます。
さつきさんは,タンクに水を \( 1050 \; mL \) 入れて,加湿器を「強」で使用したときの,タンクに残っている水の量について,使用し始めてから \( 10 \) 分おきに \( 60 \) 分後まで調べました。
次の表Ⅰは,「強」で使用したときの,経過時間とタンクに残っている水の量をまとめたものです。また,次の図は,経過時間を \( x \) 分,タンクに残っている水の量を \( y \; mL \) として,表Ⅰの結果をかき入れたものです。
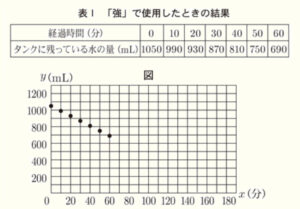
さつきさんは,図にかき入れた点が1つの直線上に並ぶので,\( y \) は \( x \) の1次関数であるとみなしました。
このとき,次の(1),(2)の問いに答えなさい。
(1) \( 1050 \; mL \) 給水されている加湿器を「強」で使用したとき,\( y \) を \( x \) の式で表しなさい。
【解説】
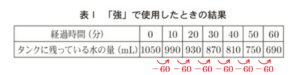
表Ⅰから,「強」で使用したとき,\( 10 \) 分使用するごとに,
タンクに残っている水の量は \( 60 \; mL \) ずつ減ったので,
\( 1 \) 分では \( 6 \; mL \) ずつの水が減ったことになります。
使用前 \( (x=0) \) のタンクの水の量は \( 1050 \; mL \) なので,
求める式は \( y=-6x+1050 \)
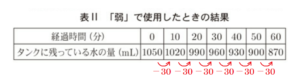
(2) さつきさんは, \( 1050 \; mL \) 給水されている加湿器を「弱」で使用したときについても調べ,表Ⅱにまとめました。
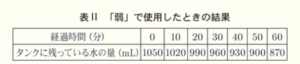
この結果から,さつきさんは,「弱」で使用したときも「強」で使用したときと同様に,\( y \) は \( x \) の1次関数であるとみなしました。
さつきさんは,\( 1050 \; mL \) 給水されている加湿器を「強」で \( 60 \) 分間使用した後,「弱」に切り替えました。このとき,タンクの水が完全になくなるまでの時間は,「強」のまま使用したときに比べ,何分長くなりますか。その時間を求めなさい。
【解説】
【「強」と「弱」を切り替えて使用したとき】
表Ⅱから,「弱」で使用したとき,\( 10 \) 分使用するごとに,
タンクに残っている水の量は \( 30 \; mL \) ずつ減ったので,
\( 1 \) 分では \( 3 \; mL \) ずつの水が減ったことになります。
「強」で \( 60 \) 分間使用した後にタンクに残っている水の量は
\( y=-6 \times 60+1050=690\; (mL) \)
「弱」で使用したときに \( 690 \; mL \) の水を使い切るのにかかる時間は,
\( 690 \div 3=230 \)(分)
よって,タンクの水が完全になくなるまでの時間は,
\( 60+230=290 \)(分)
【「強」のまま使用したとき】
タンクの水が完全になくなる( \( y=0 \) になる)までの時間は,
\( 0=-6x+1050 \)
\( 6x=1050 \)
\( x=175 \)(分)
よって,「強」と「弱」を切り替えて使用したときの方が \( 290-175=115 \)(分)長くなる。
大問11
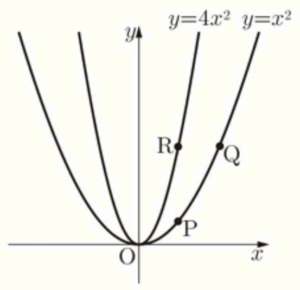
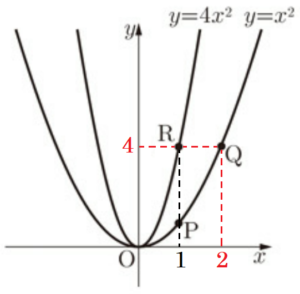
右の図のように,関数 \( y=x^2 \) のグラフ上に2点 \( P,Q \) があり,関数 \( y=4x^2 \) のグラフ上に点 \( R \) があります。3点 \( P,Q,R \) の \( x \) 座標は正であり,2点 \( P,R \) の \( x \) 座標は等しく,2点 \( Q,R \) の \( y \) 座標は等しいです。
このとき,次の(1)~(3)の問いに答えなさい。
(1) 点 \( P \) の \( x \) 座標を \( 1 \) とします。点 \( Q \) の座標を求めなさい。
【解説】
2点 \( P,R \) の \( x \) 座標は等しいことから,
点 \( R \) は,\( y=4x^2 \) 上の点で,\( x \) 座標は \( 1 \) なので,
\( y \) 座標は,
\( y=4 \times 1^2=4 \)
2点 \( Q,R \) の \( y \) 座標は等しいことから,
点 \( Q \) は,\( y=x^2 \) 上の点で,\( y \) 座標は \( 4 \) なので,
\( x \) 座標は,
\( 4=x^2 \)
\( x=2 \) ( \( x \) 座標は正のため )
よって,点 \( Q \) の座標は \( Q(2,4) \)
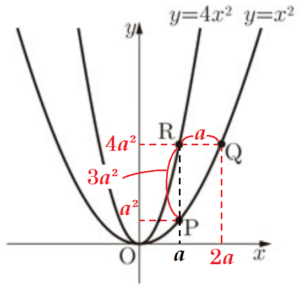
(2) 点 \( P \) の \( x \) 座標を \( a \) とします。\( △PQR \) が \( PR=QR \) の二等辺三角形になるとき,\( a \) の値を求めなさい。
【解答】
\( a=\dfrac{1}{3} \)
【解説】
(1)と同様の考え方から,
点 \( P \) の \( x \) 座標を \( a \) とするとき,
3点 \( P,Q,R \) の座標は,
\( P(a,a^2),Q(2a,4a^2),R(a,4a^2) \)
と表すことができるので,
\( PR=QR \) となるとき,
\( 4a^2-a^2=2a-a \)
\( 3a^2=a \)
\( 3a^2-a=0 \)
\( a(3a-1)=0 \)
\( a=\dfrac{1}{3} \) ( \( a>0 \) より )
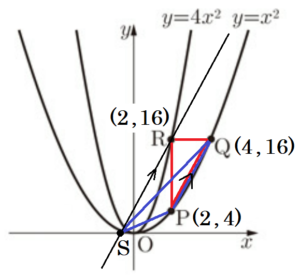
(3) 点 \( P \) の \( x \) 座標を \( 2 \) とします。\( x \) 軸上にあり,\( x \) 座標が負である点を \( S \) とします。\( △PQR \) と \( △PQS \) の面積が同じになるときの点 \( S \) の \( x \) 座標を求めなさい。
【解説】
\( △PQR \) と \( △PQS \) は辺 \( PQ \) が共通なので,等積変形の考え方から,
\( SR//PQ \) のとき,\( △PQR \) と \( △PQS \) の面積が同じになります。
(1)と同様の考え方から,
点 \( P \) の \( x \) 座標を \( 2 \) とするとき,
3点 \( P,Q,R \) の座標は,
\( P(2,4),Q(4,16),R(2,16) \)
なので,直線 \( PQ \) の傾きは
傾き \( =\dfrac{16-4}{4-2}=6 \)
直線 \( SR \) の式を \( y=6x+b \) とすると,
\( R(2,16) \) を通るので,
\( 16=6 \times 2+b \)
\( b=4 \)
よって,直線 \( SR \) の式は \( y=6x+4 \) なので,
\( x \) 軸と交わる点 \( S \) の \( x \) 座標は,
\( 0=6x+4 \)
\( 6x=-4 \)
\( x=-\dfrac{2}{3} \)
大問12
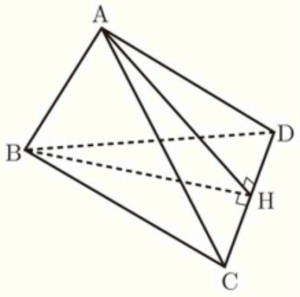
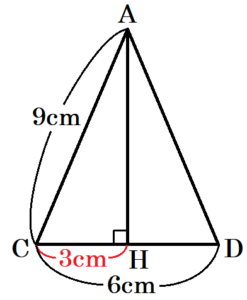
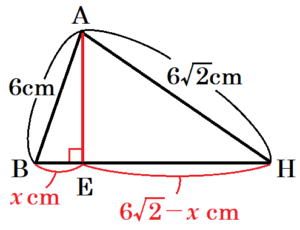
右の図は,\( AB=CD=6 \; cm \),\( AC=AD=BC=BD=9 \; cm \) の四面体 \( ABCD \) です。2つの頂点 \( A,B \) から辺 \( CD \) にそれぞれ垂線をひき,辺 \( CD \) との交点を \( H \) とします。
このとき,次の(1)~(3)の問いに答えなさい。
(1) 四面体 \( ABCD \) の面のうち,辺 \( CD \) をふくむ面をすべて書きなさい。
【解答】
面 \( ACD \),面 \( BCD \)
(2) 線分 \( AH \) の長さを求めなさい。
【解答】
\( 6\sqrt{2} \; cm \)
【解説】
面 \( ACD \) に注目すると,
\( △ACD \) は \( AC=AD \) の二等辺三角形,\( AH⊥CD \) より,
点 \( H \) は辺 \( CD \) の中点なので,
三平方の定理より,
\( AH^2=9^2-3^2=72 \)
\( AH=6\sqrt{2} \; (cm) \)
(3) 四面体 \( ABCD \) の体積を求めなさい。
【解答】
\( 18\sqrt{7} \; cm^3 \)
【解説】
\( △ACD \) と \( △BCD \) において,
仮定より,3辺の長さがそれぞれ等しいので,
\( △ACD≡△BCD \)
また,\( AH⊥CD,BH⊥CD \) より,
\( BH=AH=6\sqrt{2} \; cm \)
面 \( ABH \) に注目し,
点 \( A \) から線分 \( BH \) に垂線をひいた交点を \( E \) ,
\( BE=x \; cm \) とすると,
\( AB^2-BE^2=AH^2-EH^2 \)
\( 6^2-x^2=(6\sqrt{2})^2-(6\sqrt{2}-x)^2 \)
\( 36-x^2=72-(72-12\sqrt{2}x+x^2) \)
\( 36-x^2=12\sqrt{2}x-x^2 \)
\( 12\sqrt{2}x=36 \)
\( x=\dfrac{3}{\sqrt{2}} \; (cm) \)
このとき,線分 \( AE \) の長さは,
\( AE^2=6^2- \left(\dfrac{3}{\sqrt{2}} \right)^2=\dfrac{63}{2} \)
\( AE=\dfrac{3\sqrt{7}}{\sqrt{2}} \; (cm) \)
よって,四面体 \( ABCD \) の体積は,
\( \left( 6 \times 6\sqrt{2} \times \dfrac{1}{2} \right) \times \dfrac{3\sqrt{7}}{\sqrt{2}} \times \dfrac{1}{3}=18\sqrt{2} \times \dfrac{\sqrt{7}}{\sqrt{2}}=18\sqrt{7} \; (cm^3) \)