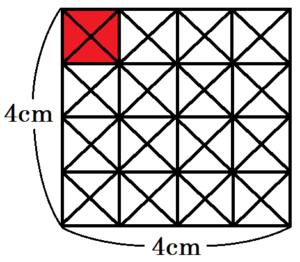
大問1
1 \( 3-(-5) \) を計算しなさい。
2 \( 8a^3b^2 \div 6ab \) を計算しなさい。
【解答】
\( \dfrac{4}{3}a^2b \)
【解説】
\( =\dfrac{8a^3b^2}{6ab} \)
\( =\dfrac{4}{3}a^2b \)
3 \( (x+3)^2 \) を展開しなさい。
4 1個 \( x \) 円のパンを7個と1本 \( y \) 円のジュースを5本買ったところ,代金の合計が2000円以下になった。この数量の関係を不等式で表しなさい。
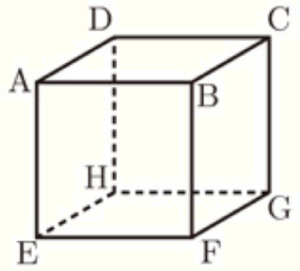
5 右の図の立方体 \( ABCD-EFGH \) において,辺 \( AB \) とねじれの位置にある辺の数はいくつか。
【解説】
ねじれの位置にある直線は,
どこまでいっても交わらない直線のうち,平行ではないもの
なので,\( DH,CG,EH,FG \) の4つになります。

6 \( y \) は \( x \) に反比例し,\( x=-2 \) のとき \( y=8 \) である。\( y \) を \( x \) の式で表しなさい。
【解答】
\( y=-\dfrac{16}{x} \)
【解説】
反比例の式を \( y=\dfrac{a}{x} \) とし,\( x=-2,y=8 \) を代入すると,
\( 8=\dfrac{a}{-2} \)
\( a=-16 \)
よって,求める式は,\( y=-\dfrac{16}{x} \)
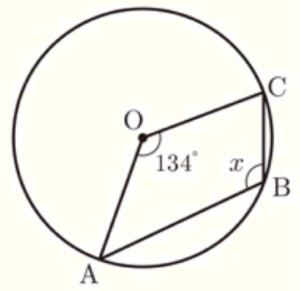
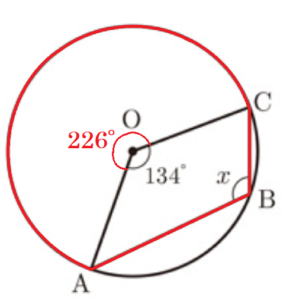
7 右の図において,点 \( A,B,C \) は円 \( O \) の周上の点である。
\( ∠x \) の大きさを求めなさい。
【解説】
弧 \( AC \) のうち,点 \( B \) を含まない方に対する中心角は
\( 360°-134°=226° \)
よって,円周角は中心角の半分になるので,
\( ∠x=\dfrac{1}{2} \times 226°=113° \)
8 \( △ABC \) と \( △DEF \) は相似であり,その相似比は \( 3:5 \) である。このとき,\( △DEF \) の面積は \( △ABC \) の面積の何倍か求めなさい。

【解答】
\( \dfrac{25}{9} \) 倍
【解説】
相似な三角形の面積比は,相似比の2乗の比になるので,
\( △ABC:△DEF=3^2:5^2=9:25 \)
\( 9△DEF=25△ABC \)
\( △DEF=\dfrac{25}{9}△ABC \)
大問2
1 2次方程式 \( x^2+4x+1=0 \) を解きなさい。
【解説】
この2次方程式を \( ax^2+bx+c=0 \) と考えると, \( a=1,b=4,c=1 \) なので,
解の公式より,
\( x=\dfrac{-b±\sqrt{b^2-4ac}}{2a} \)
\( =\dfrac{-4±\sqrt{4^2-4 \times 1 \times 1}}{2 \times 1} \)
\( =\dfrac{-4±2\sqrt{3}}{2} \)
\( =-2±\sqrt{3} \)
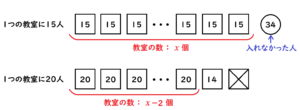
2 ある高校では,中学生を対象に一日体験学習を各教室で実施することにした。使用できる教室の数と参加者の人数は決まっている。1つの教室に入る参加者を15人ずつにすると,34人が教室に入れない。また,1つの教室に入る参加者を20人ずつにすると,14人の教室が1つだけでき,さらに使用しない教室が1つできる。
このとき,使用できる教室の数を \( x \) として方程式をつくり,使用できる教室の数を求めなさい。ただし,途中の計算も書くこと。
【解答】
\( 15x+34=20(x-2)+14 \)
\( 15x+34=20x-26 \)
\( 5x=60 \)
\( x=12 \)
よって,使用できる教室の数は12個
【解説】
参加者の人数を図を使って表してみます。
3 次の先生と生徒の会話文を読んで,下の 内の生徒が完成させた【証明】の ➀ から ➄ に当てはまる数や式をそれぞれ答えなさい。
先生 「一の位が \( 0 \) でない \( 900 \) 未満の3けたの自然数を \( M \) とし,\( M \) に \( 99 \) をたしてできる
自然数を \( N \) とすると,\( M \) の各位の数の和と \( N \) の各位の数の和は同じ値になるという
性質があります。例として \( 583 \) で確かめてみましょう。」
生徒 「 \( 583 \) の各位の数の和は \( 5+8+3=16 \) です。\( 583 \) に \( 99 \) をたすと \( 682 \) となるので,
各位の数の和は \( 6+8+2=16 \) で同じ値になりました。」
先生 「そうですね。それでは,\( M \) の百の位,十の位,一の位の数をそれぞれ \( a,b,c \) として,
この性質を証明してみましょう。\( a,b,c \) のとりうる値の範囲に気をつけて,\( M \) と \( N \) を
それぞれ \( a,b,c \) を用いて表すとどうなりますか。」
生徒 「 \( M \) は表せそうですが,\( N \) は \( M+99 \) で・・・,各位の数がうまく表せません。」
先生 「 \( 99 \) を \( 100-1 \) におきかえて考えてみましょう。」
生徒が完成させた【証明】
3けたの自然数 \( M \) の百の位,十の位,一の位の数をそれぞれ \( a,b,c \) とすると,\( a \) は \( 1 \) 以上 \( 8 \) 以下の整数,\( b \) は \( 0 \) 以上 \( 9 \) 以下の整数,\( c \) は \( 1 \) 以上 \( 9 \) 以下の整数となる。
このとき,
\( M= \) ➀ \( \times \;\; a \;\; + \) ➁ \( \times \;\; b \;\; + \;\; c \) と表せる。
また,\( N=M+99 \) より
\( N= \) ➀ \( \times \;\; a \;\; + \) ➁ \( \times \;\; b \;\; + \;\; c \;\; + \;\; 100 \;\; – \;\; 1 \) となるから
\( N= \) ➀ \( \times \;\; ( \) ➂ \( ) \;\; + \) ➁ \( \times \) ➃ \( + \) ➄ となり,
\( N \) の百の位の数は ➂ ,十の位の数は ➃ ,一の位の数は ➄ となる。
よって, \( M \) の各位の数の和と \( N \) の各位の数の和はそれぞれ \( a+b+c \) となり,同じ値になる。
【解答】
➀ ・・・ \( 100 \)
➁ ・・・ \( 10 \)
➂ ・・・ \( a+1 \)
➃ ・・・ \( b \)
➄ ・・・ \( c-1 \)
大問3
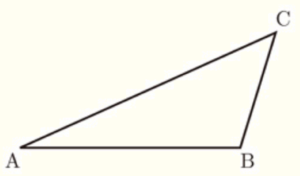
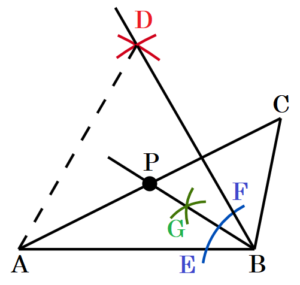
1 右の図の \( △ABC \) において,辺 \( AC \) 上にあり,\( ∠ABP=30° \) となる点 \( P \) を作図によって求めなさい。ただし,作図には定規とコンパスを使い,また,作図に用いた線は消さないこと。
【解答】
手順1 点 \( A,B \) を中心に線分 \( AB \) を半径とする円弧を描く
(交点を点 \( D \) とします)
手順2 点 \( B \) を中心に円弧を描く
(交点を点 \( E,F \) とします)
手順3 点 \( E,F \) を中心に円弧を描く
(交点を点 \( G \) とします)
手順4 2点 \( B,G \) を通る直線を描く
手順4の直線と辺 \( AC \) との交点が求める点 \( P \) になります。
【解説】
\( △ABC \) の辺の長さも角度も一切わからないので,
\( 60° \) の角をつくって,二等分線をひくことで求めることを考えます。
\( 60° \) といえば,\( 30°,60°,90° \) の直角三角形か正三角形になります。
線分 \( AB \) が半径となるような円弧を描くと,正三角形 \( ABD \) をつくることができます。
正三角形の1つの角は \( 60° \) なので,\( ∠ABD=60° \) であり,
\( ∠ABD \) の二等分線と辺 \( AC \) との交点が求める点 \( P \) になります。
2 右の図は,\( AB=2 \; cm,BC=3 \; cm,CD=3 \; cm, \)
\( ∠ABC=∠BCD=90° \) の台形 \( ABCD \) である。
このとき,次の (1) ,(2) の問いに答えなさい。
(1) \( AD \) の長さを求めなさい。
【解答】
\( \sqrt{10} \; cm \)
【解説】
点 \( A \) から線分 \( CD \) に垂線をひき,交点を \( E \) とすると,
\( AE=3 \; cm,DE=1 \; cm \) なので,三平方の定理より,
\( AD^2=3^2+1^2=10 \)
\( AD=\sqrt{10} \; (cm) \)( \( AD>0 \) より)
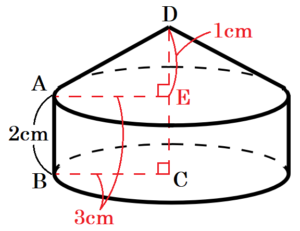
(2) 台形 \( ABCD \) を,辺 \( CD \) を軸として1回転させてできる立体の体積を求めなさい。ただし,円周率は \( \pi{} \) とする。
【解答】
\( 21\pi{} \; cm^3 \)
【解説】
台形 \( ABCD \) を,辺 \( CD \) を軸として1回転させてできる立体は,
右の図のように,
「半径 \( 3 \; cm \),高さ \( 2 \; cm \) の円柱」と
「半径 \( 3 \; cm \),高さ \( 1 \; cm \) の円すい」
をくっつけたものになります。
円柱の体積 \( =\pi{} \times 3^2 \times 2=18\pi{} \; (cm^3) \)
円すいの体積 \( =\pi{} \times 3^2 \times 1 \times \dfrac{1}{3}=3\pi{} \; (cm^3) \)
よって,求める体積は,\( 18\pi{}+3\pi{}=21\pi{} \; (cm^3) \)
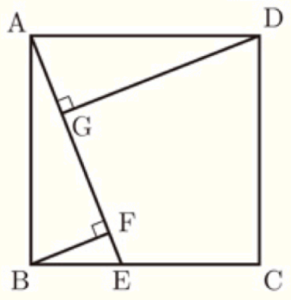
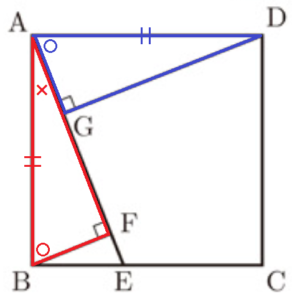
3 右の図のように,正方形 \( ABCD \) の辺 \( BC \) 上に点 \( E \) をとり,頂点 \( B,D \) から線分 \( AE \) にそれぞれ垂線 \( BF,DG \) をひく。
このとき,\( △ABF≡△DAG \) であることを証明しなさい。
【解答】
\( △ABF \) と \( △DAG \) において,
正方形のすべての辺の長さは等しいので,\( AB=DA \) ・・・ ①
仮定より,\( ∠AFB=∠DGA=90° \) ・・・ ➁
三角形の内角の和は \( 180° \) なので,
\( ∠ABF=180°-(90°+∠BAF) \)
\( =90°-∠BAF \) ・・・ ➂
正方形の内角はすべて \( 90° \) なので,
\( ∠DAG=90°-∠BAF \) ・・・ ➃
➂➃より,\( ∠ABF=∠DAG \) ・・・ ➄
①➁➄より,斜辺と他の1鋭角が等しい直角三角形なので,
\( △ABF≡△DAG \)
大問4
1 5人の生徒 \( A,B,C,D,E \) がいる。これらの生徒の中から,くじびきで2人を選ぶとき,\( D \) が選ばれる確率を求めなさい。
【解説】
2人を選ぶ組み合わせを樹形図として書き出し,\( D \) が含まれるところに
○ をつけます。
\( D \) が含まれる組み合わせは4通り,すべての組み合わせは10通りなので,
求める確率は,\( \dfrac{4}{10}=\dfrac{2}{5} \)

2 右の表は,あるクラスの生徒 \( 35 \) 人が水泳の授業で \( 25 \; m \) を泳ぎ,タイムを計測した結果を度数分布表にまとめたものである。
このとき,次の (1),(2) の問いに答えなさい。
(1) \( 18.0 \) 秒以上 \( 20.0 \) 秒未満の階級の累積度数を求めなさい。
【解説】
累積度数は求める階級以下のすべての階級の度数の和になるので,
\( 2+7+8=17 \)(人)
(2) 度数分布表における,最頻値を求めなさい。
【解説】
最頻値は,度数が最も多い階級の階級値なので,あてはまる階級は \( 20.0 \) 秒以上 \( 22.0 \) 秒未満です。
この階級の階級値は,\( \dfrac{20.0+22.0}{2}=21.0 \)(秒)になります。
3 下の図は,ある中学校の3年生100人を対象に20点満点の数学のテストを2回実施し,1回目と2回目の得点のデータの分布のようすをそれぞれ箱ひげ図にまとめたものである。

このとき,次の (1),(2) の問いに答えなさい。
(1) 箱ひげ図から読み取れることとして正しいことを述べているものを,次の ア,イ,ウ,エ の中から2つ選び,記号で答えなさい。
ア 中央値は,1回目よりも2回目の方が大きい。
イ 最大値は,1回目よりも2回目の方が小さい。
ウ 範囲は,1回目よりも2回目の方が大きい。
エ 四分位範囲は,1回目よりも2回目の方が小さい。
【解説】
ア 中央値は,1回目が \( 13 \) 点,2回目が \( 14 \) 点
イ 最大値は,1回目が \( 18 \) 点,2回目が \( 20 \) 点
ウ 範囲は,最大値 \( – \) 最小値 で求められので,
1回目が \( 18-6=12 \)(点),2回目が \( 20-8=12 \)(点)
エ 四分位範囲は,第三四分位数 \( – \) 第一四分位数 で求められるので,
1回目が \( 16-8=8 \)(点),2回目が \( 16-10=6 \)(点)
(2) 次の文章は,「1回目のテストで8点を取った生徒がいる」ことが正しいとは限らないことを説明したものである。 に当てはまる文を,特定の2人の生徒に着目して書きなさい。
箱ひげ図から,1回目の第1四分位数が8点であることがわかるが,8点を取った生徒がいない場合も考えられる。例えば,テストの得点を小さい順に並べたときに, の場合も,第1四分位数が8点となるからである。
【解答】
25番目の生徒の得点が7点,26番目の生徒の得点が9点
【解説】
データの総数が100人なので,第一四分位数は,得点の低い方から25番目の人と26番目の人の得点の平均値になります。
大問5
1 右の図のように,2つの関数 \( y=5x,y=2x^2 \) のグラフ上で, \( x \) 座標が \( t \; (t>0) \) である点をそれぞれ \( A,B \) とする。\( B \) を通り \( x \) 軸に平行な直線が,関数 \( y=2x^2 \) のグラフと交わる点のうち,\( B \) と異なる点を \( C \) とする。また,\( C \) を通り \( y \) 軸に平行な直線が,関数 \( y=5x \) のグラフと交わる点を \( D \) とする。
このとき,次の (1),(2),(3) の問いに答えなさい。
(1) 関数 \( y=2x^2 \) について,\( x \) の変域が \( -1≦x≦5 \) のときの \( y \) の変域を求めなさい。
【解説】
関数 \( y=ax^2 \; (a>0) \) について,\( x \) の変域が \( 0 \) を含むとき,
\( y \) の最小値は必ず \( 0 \) になります。
また,\( x \) の絶対値が最も大きくなるとき,\( y \) は最大値をとります。
\( -1≦x≦5 \) の範囲で,絶対値が最も大きくなるのは,
\( x=5 \) のときなので,
\( y=2 \times 5^2=50 \)
よって,\( y \) の変域は,\( 0≦y≦50 \)
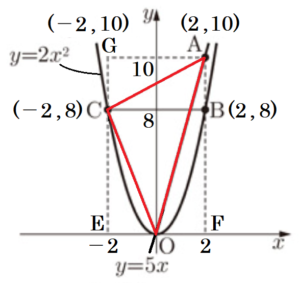
(2) \( t=2 \) のとき,\( △OAC \) の面積を求めなさい。
【解説】
点 \( B \) は \( y=2x^2 \) 上の点で,\( x=2 \) なので,
\( y=2 \times 2^2=8 \)
点 \( C \) は \( y=2x^2 \) 上の点で,
点 \( B \) と \( y \) 座標の値が等しいので,
\( x \) 座標の値は,点 \( B \) の \( x \) 座標の符号を入れ替えたものとなり,\( x=-2 \)
点 \( A \) は \( y=5x \) 上の点で,\( x=2 \) なので,
\( y=5 \times 2=10 \)
さらに,右の図のように点 \( E,F,G \) をとると,
\( E(-2,0),F(2,0),G(-2,10) \) となります。
\( △OAC \) の面積は,
四角形 \( EFAG-(△AGC+△CEO+△AFO) \)
で求めることができるので,
四角形 \( EFAG=4 \times 10=40 \)
\( △AGC=4 \times 2 \times \dfrac{1}{2}=4 \)
\( △CEO=2 \times 8 \times \dfrac{1}{2}=8 \)
\( △AFO=2 \times 10 \times \dfrac{1}{2}=10 \)
より,
\( △OAC=40-(4+8+10)=18 \)
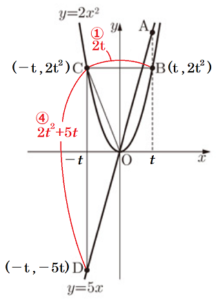
(3) \( BC:CD=1:4 \) となるとき,\( t \) の値を求めなさい。ただし,途中の計算も書くこと。
【解答】
\( t=\dfrac{3}{2} \)
【解説】
点 \( B \) は \( y=2x^2 \) 上の点なので,
\( x \) 座標の値が \( t \) のときの \( y \) 座標の値は,
\( 2t^2 \) と表すことができます。
点 \( C \) も \( y=2x^2 \) 上の点で,
\( y \) 座標の値は点 \( B \) と等しいので,
\( x \) 座標の値は \( -t \) と表すことができます。
点 \( D \) は \( y=5x \) 上の点で,
\( x \) 座標の値は \( -t \) なので,
\( y \) 座標の値は,\( -5t \) と表すことができます。
このとき,
\( BC=t-(-t)=2t \)
\( CD=2t^2-(-5t)=2t^2+5t \)
なので,
\( BC:CD=1:4 \)
\( 2t:(2t^2+5t)=1:4 \)
\( 2t^2+5t=8t \)
\( 2t^2-3t=0 \)
\( t(2t-3)=0 \)
\( t=0,\dfrac{3}{2} \)
\( t>0 \) より,あてはまるのは,\( t=\dfrac{3}{2} \)
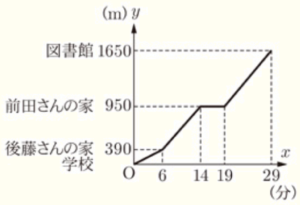
2 ある日の放課後,前田さんは友人の後藤さんと図書館に行くことにした。学校から図書館までの距離は \( 1650 \; m \) で,その間に後藤さんの家と前田さんの家がこの順に一直線の道沿いにある。
2人は一緒に学校を出て一定の速さで \( 6 \) 分間歩いて,後藤さんの家に着いた。後藤さんが家で準備をするため,2人はここで別れた。その後,前田さんは毎分 \( 70 \; m \) の速さで8分間歩いて自分の家に着き,家に着いてから \( 5 \) 分後に毎分 \( 70 \; m \) の速さで図書館に向かった。
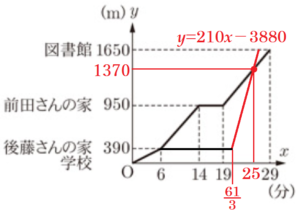
右の図は,前田さんが図書館に着くまでのようすについて,学校を出てからの時間を \( x \) 分,学校からの距離を \( y \; m \) として,\( x \) と \( y \) の関係をグラフに表したものである。
このとき,次の (1),(2),(3) の問いに答えなさい。
(1) 2人が学校を出てから後藤さんの家に着くまでの速さは毎分何 \( m \) か。
【解説】
\( 390 \; m \) を \( 6 \) 分かけて歩いたので,
\( 390 \div 6=65 \)
よって,後藤さんの家に着くまでの速さは毎分 \( 65 \; m \)
(2) 前田さんが後藤さんと別れてから自分の家に着くまでの\( x \) と \( y \) の関係を式で表しなさい。
ただし,途中の計算も書くこと。
【解説】
後藤さんと別れてから,前田さんは毎分 \( 70 \; m \) の速さで歩いたので,
求める直線の式を \( y=70x+b \) とし,\( x=6,y=390 \) を代入すると,
\( 390=70 \times 6+b \)
\( b=-30 \)
よって,求める直線の式は \( y=70x-30 \)
(3) 後藤さんは準備を済ませ,自転車に乗って毎分 \( 210 \; m \) の速さで図書館に向かい,図書館まで残り \( 280 \; m \) の地点で前田さんに追いついた。後藤さんが図書館に向かうために家を出たのは,家に着いてから何分何秒後か。
【解答】
\( 14 \) 分 \( 20 \) 秒後
【解説】
後藤さんが前田さんに追いついた場所に前田さんがいるのは,図書館に着く \( 280 \div 70=4 \) 分前なので,追いついた時間は学校を出てから \( 29-4=25 \) 分後です。
追いついた場所は,学校から \( 1650-280=1370 \; (m) \) の地点なので,
後藤さんが自転車で進んだ状態を表す直線(赤の直線)は \( (25,1370) \) を通ります。
後藤さんは毎分 \( 210 \; m \) の速さで進んだので,
この直線の式を \( y=210x+b \) とし,
\( x=25,y=1370 \) を代入すると,
\( 1370=210 \times 25+b \)
\( b=-3880 \)
よって,この直線の式は \( y=210x-3880 \)
ここに, 後藤さんの家の場所を表す \( y=390 \) を代入すると,
\( 390=210 \times x-3880 \)
\( 210x=4270 \)
\( x=\dfrac{61}{3} \)
となり,後藤さんが家を出たのは,学校を出てから \( \dfrac{61}{3} \) 分後であるとわかります。
後藤さんが家に着いたのは学校を出てから \( 6 \) 分後なので,
家に着いてからの時間は \( \dfrac{61}{3}-6=\dfrac{43}{3}=14+\dfrac{1}{3} \) 分後
\( \dfrac{1}{3} \) 分を秒に換算すると,\( \dfrac{1}{3} \times 60=20 \) 秒なので,
求める時間は \( 14 \) 分 \( 20 \) 秒後になります。
大問6
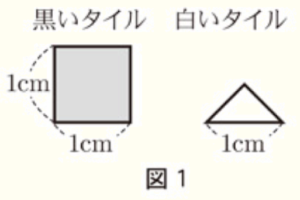
1辺の長さが \( n \; cm \)(\( n \) は2以上の整数)の正方形の板に,図1のような1辺の長さが \( 1 \; cm \) の正方形の黒いタイル,または斜辺の長さが \( 1 \; cm \) の直角二等辺三角形の白いタイルを貼る。板にタイルを貼るときは,黒いタイルを1枚使う【貼り方Ⅰ】,または白いタイルを4枚使う【貼り方Ⅱ】を用いて,タイルどうしが重ならないように板にすき間なくタイルをしきつめることとする。

例えば, \( n=3 \) の場合について考えるとき,図2は黒いタイルを7枚,白いタイルを8枚,合計15枚のタイルを使って板にタイルをしきつめたようすを表しており,図3は黒いタイルを4枚,白いタイルを20枚,合計 24枚のタイルを使って板にタイルをしきつめたようすを表している。

このとき,次の1,2,3の問いに答えなさい。
1 \( n=4 \) の場合について考える。白いタイルだけを使って板にタイルをしきつめたとき,使った白いタイルの枚数を求めなさい。
【解説】
ここでは,1辺 \( 1 \; cm \) の正方形1個を「1マス」と呼ぶことにします。
\( n=4 \) の場合,板は1辺 \( 4 \; cm \) の正方形なので,
16マス分の大きさになります。
1マスに使う白いタイルの枚数は \( 4 \) 枚なので,
板全体を埋めるのに使った白いタイルの枚数は,
\( 4 \times 16=64 \)(枚)
になります。
2 \( n=5 \) の場合について考える。黒いタイルと白いタイルを合計 ( 49 \) 枚使って板にタイルをしきつめたとき,使った黒いタイルと白いタイルの枚数をそれぞれ求めなさい。
【解答】
黒いタイル ・・・ \( 17 \) 枚
白いタイル ・・・ \( 32 \) 枚
【解説】
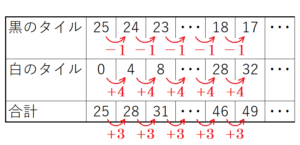
使った黒いタイルと白いタイルの枚数によって,合計のタイルの枚数がどのように変化するかを
表として書いてみます。
すべて黒いタイルを使ったとき,使う枚数は \( 25 \) 枚になります。
ここから,黒いタイルを \( 1 \) 枚減らして白いタイルにおきかえると,
黒いタイルを \( 24 \) 枚,白いタイルを \( 1 \times 4=4 \) 枚で,合計 \( 28 \) 枚使うことになります。
また,黒いタイルを \( 2 \) 枚減らして白いタイルにおきかえると,
黒いタイルを \( 23 \) 枚,白いタイルを \( 2 \times 4=8 \) 枚で,合計 \( 31 \) 枚使うことになります。
このように,黒いタイルの枚数が \( 1 \) 枚減るごとに合計のタイルの枚数は \( 3 \) 枚ずつ増えています。
よって,合計のタイルの枚数が \( 49-25=24 \) 枚増えるのは,
黒いタイルの枚数が \( 24 \div 3=8 \) 枚減ったときなので,
黒いタイルが \( 25-8=17 \) 枚,白いタイルを \( 8 \times 4=32 \) 枚使うときになります。
3 次の文章の ➀ , ➁ , ➂ に当てはまる式や数をそれぞれ求めなさい。ただし,文章中の \( a \) は \( 2 \) 以上の整数,\( b \) は \( 1 \) 以上の整数とする。
\( n=a \) の場合について考える。はじめに,黒いタイルと白いタイルを使って板にタイルをしきつめたとき,使った黒いタイルの枚数を \( b \) 枚とすると,使った白いタイルの枚数は \( a \) と \( b \) を用いて ➀ 枚と表せる。
次に,この板の【貼り方Ⅰ】のところを【貼り方Ⅱ】に,【貼り方Ⅱ】のところを【貼り方Ⅰ】に変更した新しい正方形の板を作った。このときに使ったタイルの枚数の合計は,はじめに使ったタイルの枚数の合計よりも225枚少なくなった。これを満たす \( a \) のうち,最も小さい値は ➁ ,その次に小さい値は ➂ である。
【解答】
➀ ・・・ \( 4(a^2-b) \) 枚
➁ ・・・ \( 9 \)
➂ ・・・ \( 11 \)
【解説】
➀
\( n=a \) の場合,板の大きさは \( a^2 \) マス分なので,黒いタイルを \( b \) 枚使うとき,
白いタイルを使うのは \( a^2-b \) マスになります。
1マスあたり,白いタイルは \( 4 \) 枚ずつ使うので,白いタイルの総数は,\( 4(a^2-b) \) 枚になります。
➁ , ➂
黒いタイルを \( b \) 枚使うとき,白いタイルは \( 4(a^2-b) \) 枚使うので,
すべてのタイルの枚数の合計は,\( b+4(a^2-b) \) になります。
【貼り方Ⅰ】と【貼り方Ⅱ】を入れ替えたときは,
白いタイルを \( b \) マス分使うので,白いタイルは \( 4b \) 枚使います。
残りの \( a^2-b \) マスには黒いタイルを使うので,\( a^2-b \) 枚となり,
すべてのタイルの枚数の合計は,\( a^2-b+4b \) になります。
これらから,すべてのタイルの枚数の合計について方程式をたてると,
\( \{b+4(a^2-b)\}-(a^2-b+4b)=225 \)
\( (4a^2-3b)-(a^2+3b)=225 \)
\( 3a^2-6b=225 \)
\( a^2-2b=75 \)
\( a^2=75+2b \)
ここで,\( b \) は \( 1 \) 以上の整数なので,\( 2b \) は偶数であり,\( 75+2b \) は \( 75 \) より大きい奇数になります。
また,\( a^2 \) について考えると,\( 8^2=64,9^2=81 \) より,\( a \) は \( 9 \) 以上の整数になります。
さらに,
\( a \) が偶数の場合,\( a^2 \) は,偶数 \( \times \) 偶数 \( = \) 偶数
\( a \) が奇数の場合,\( a^2 \) は,奇数 \( \times \) 奇数 \( = \) 奇数
となるので,\( a \) は \( 9 \) 以上の奇数であるとわかります。
よって,\( a^2 \) が \( 75 \) より大きい奇数になるような \( a \) のうち,
最も小さい値は \( 9 \),その次に小さい値は \( 11 \) になります。