長野県公立高校入試　令和７（2025）年度　解答＆解説

\( ∠BAC=40° \) は \( \stackrel{\huge\frown}{ BC } \) に対する円周角，
\( ∠BOC \) は \( \stackrel{\huge\frown}{ BC } \) に対する中心角なので，
　\( ∠BOC=2∠BAC=80° \)

線分 \( OB，OC \) は円 \( O \) の半径であることから，\( △OBC \) は二等辺三角形なので，
　\( ∠x=\dfrac{180°-∠BOC}{2}=50° \)

手順１　２点 \( O，P \) を中心に線分 \( OP \) を
　　　　半径とする円弧を描く
　　　　（交点を \( A \) とします）
手順２　２点 \( O，A \) を通る直線を描く
手順３　２点 \( A，P \) を中心に円弧を描く
　　　　（交点を \( B \) とします）
手順４　２点 \( O，B \) を通る直線を描く

２つのさいころをＡ，Ｂとして，２つのさいころの出る目の組み合わせとその積を表に書き出し，
積が \( 12 \) になるところに 〇 をつけると，
右のようになります。

全ての組み合わせは \( 36 \) 通り，
積が \( 12 \) になる組み合わせは \( 4 \) 通りなので，
求める確率は \( \dfrac{4}{36}=\dfrac{1}{9} \)

度数分布表では，すべての階級の相対度数の合計は
必ず \( 1 \) になります。
３回の階級の相対度数を \( x \) とすると，
　\( 0,15+0,40+0,25+x=1 \)
　　　　　　　　　　　　　\( x=0,20 \)

四分位範囲の大きさは，箱ひげ図の箱の部分の
長さが長い（高さが高い）ほど大きくなります。

箱ひげ図から，Ａの方がＢより箱の部分の高さは低いので，四分位範囲は小さいと判断できます。

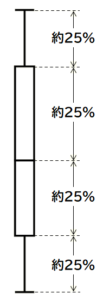
また，四分位範囲の中（箱の中）には全体の約５０％の個数の値が含まれます。

つまり，Ａの方がＢより小さい箱の中に１３個の値を含んでいるので，それぞれの値の散らばりの程度も小さいといえます。

点 \( A \) は \( y=\dfrac{1}{2}x^2 \) 上の点で， \( x \) 座標の値が \( 4 \)
なので，\( y \) 座標の値は，
　\( y=\dfrac{1}{2} \times 4^2=8 \)
であり，点 \( A \) の座標は \( A(4，8) \)
ここから，直線 \( OA \) の式は \( y=2x \)

点 \( Q \) は \( y=2x \) 上の点で，\( x \) 座標の値が \( 6 \)
なので，\( y \) 座標の値は，
　\( y=2 \times 6=12 \)
であり，点 \( Q \) の座標は \( Q(6，12) \)

点 \( R \) は \( y=\dfrac{1}{2}x^2 \) 上の点で，\( x \) 座標の値が \( 6 \)
なので，\( y \) 座標の値は，
　\( y=\dfrac{1}{2} \times 6^2=18 \)
であり，点 \( R \) の座標は \( R(6，18) \)

点 \( P \) の \( x \) 座標を \( s \) とすると，
点 \( Q \) の \( y \) 座標は \( 2s \)，
点 \( R \) の \( y \) 座標は \( \dfrac{1}{2}s^2 \)
と表すことができるので，
　\( PQ=2s \)
　\( QR=\dfrac{1}{2}s^2-2s \)
と表すことができます。

以上より，
　　　　\( PQ=QR \)
　　　　 \( 2s=\dfrac{1}{2}s^2-2s \)
　\( \dfrac{1}{2}s^2-4s=0 \)
　　\( s^2-8s=0 \)
　 \( s(s-8)=0 \)
　　　　　\( s=0，8 \)
\( s \) は正の数なので，あてはまるのは \( s=8 \)
よって，求める点 \( P \) の \( x \) 座標は \( 8 \) になります。

点 \( C \) から線分 \( AB \) に垂線をひき，
交点を \( M \) とすると，
\( △MBC \) は，\( BM=CM=4 \; cm \) の直角二等辺三角形になっているので，
　\( BC=\sqrt{2}CM=4\sqrt{2} \; (cm) \)

よって，四角形 \( ABCD \) の面積は，
　\( 4\sqrt{2} \times 4=16\sqrt{2} \; (cm^2) \)

\( △ABE \) と \( △PCE \) において，
対頂角は等しいので，\( ∠AEB=∠PEC \) ･･･ ➀
長方形の向かい合う辺は平行なので，
\( AB//PC \) であり，
錯角は等しいので，\( ∠ABE=∠PCE \) ･･･ ➁
➀➁より，２組の角がそれぞれ等しいので，
　\( △ABE \) ∽ \( △PCE \)

補助線 \( AC \) をひくと，
\( △ABE \) と \( △ACE \) において，
長方形の内角は \( 90° \) なので，
　\( ∠AEB=∠AEC=90° \) ･･･ ➀
\( △ABE≡△PCE \) より，
　\( BE=CE \) ･･･ ➁
また，\( AE \) は共通 ･･･ ➂
➀➁➂より，
２組の辺とその間の角がそれぞれ等しいので，
　\( △ABE≡△ACE \)
対応する辺は等しいので，\( AB=AC \) ･･･ ➃

点 \( B \) から線分 \( CP \) に垂線をひき，
交点を \( H \) とすると，
\( △ABE \) と \( △BCH \) において，
長方形ア，イのリボンの幅を表しているので，
　\( AE=BH=4 \; cm \) ･･･ ➄
　\( ∠AEB=∠BHC=90° \) ･･･ ⑥
三角形の内角の和は \( 180° \) なので，
　\( ∠BAE=90°-∠ABE \) ･･･ ⑦
\( ∠ABH=90° \) でもあるので，
　\( ∠CBH=90°-∠ABE \) ･･･ ⑧
⑦⑧より，
　\( ∠BAE=∠CBH \) ･･･ ➈
➄⑥➈より，
１組の辺とその両端の角がそれぞれ等しいので，
　\( △ABE≡△BCH \)
対応する辺は等しいので，\( AB=BC \) ･･･ ➉

\( △PDA \) において，
\( △ABE≡△PCE \) より，
　\( ∠CPE=∠BAE=30° \)
長方形 \( AEFG \) の内角なので，
　\( ∠PAD=90° \)
以上より，\( △PDA \) は
\( 30°，60°，90° \) の直角三角形になっています。

\( △ABE≡△PCE \) より，
\( AE≡PE=4 \; cm \) であり，\( PA=8 \; cm \) なので，
　\( PD=\dfrac{2}{\sqrt{3}}PA=\dfrac{16\sqrt{3}}{3} \; (cm) \)

（２）➀より，\( △ABE≡△BCH \) なので，
\( AB=BC \) になっています。
\( △ABE \) において，\( BE=x \; cm \) とすると，
三平方の定理より，
　\( AB^2=x^2+4^2 \)
また，\( BC=x+3 \; cm \) と表すことができるので，
　\( BC^2=(x+3)^2 \)
\( AB=BC \) より，\( AB^2=BC^2 \) なので，
　　 \( AB^2=BC^2 \)
　\( x^2+4^2=(x+3)^2 \)
　\( x^2+16=x^2+6x+9 \)
　　　 \( 6x=7 \)
　　　　\( x=\dfrac{7}{6} \; (cm) \)

よって，
　\( BE：EC=x：3 \)
　　　　　　\( =\dfrac{7}{6}：3 \)
　　　　　　\( =7：18 \)