大問1
(1) \( -8-(-2)+3 \) を計算しなさい。
【解説】
\( =-8+2+3 \)
\( =3 \)
(2) \( 28x^2 \div 7x \) を計算しなさい。
【解説】
\( =28x^2 \times \dfrac{1}{7x} \)
\( =4x \)
(3) \( \sqrt{50}-\dfrac{6}{\sqrt{2}} \) を計算しなさい。
【解説】
\( =5\sqrt{2}-\dfrac{6 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} \)
\( =5\sqrt{2}-3\sqrt{2} \)
\( =2\sqrt{2} \)
(4) \( (x-6y)^2 \) を展開しなさい。
【解答】
\( x^2-12xy+36y^2 \)
(5) 方程式 \( x^2+3x-5=0 \) を解きなさい。
【解答】
\( \dfrac{-3±\sqrt{29}}{2} \)
【解説】
\( ax^2+bx+c=0 \) と考えると,\( a=1,b=3,c=-5 \) となるので,
解の公式より,
\( x=\dfrac{-3±\sqrt{3^2-4 \times 1 \times (-5)}}{2 \times 1} \)
\( =\dfrac{-3±\sqrt{29}}{2} \)
(6) 関数 \( y=\dfrac{16}{x} \) のグラフ上の点で,\( x \) 座標と \( y \) 座標がともに整数である点は何個ありますか。
【解説】
\( x \) 座標と \( y \) 座標がともに整数になるのは,\( x \) の値が \( 16 \) の約数になるときです。
\( 16 \) の約数は,\( 1,2,4,8,16,-1,-2,-4,-8,-16 \) なので,
以下の10個になります。
\( x=1 \) のとき,\( y=\dfrac{16}{1}=16 \), \( x=-1 \) のとき,\( y=\dfrac{16}{-1}=-16 \),
\( x=2 \) のとき,\( y=\dfrac{16}{2}=8 \), \( x=-2 \) のとき,\( y=\dfrac{16}{-2}=-8 \),
\( x=4 \) のとき,\( y=\dfrac{16}{4}=4 \), \( x=-4 \) のとき,\( y=\dfrac{16}{-4}=-4 \),
\( x=8 \) のとき,\( y=\dfrac{16}{8}=2 \), \( x=-8 \) のとき,\( y=\dfrac{16}{-8}=-2 \),
\( x=16 \) のとき,\( y=\dfrac{16}{16}=1 \), \( x=-16 \) のとき,\( y=\dfrac{16}{-16}=-1 \),
(7) 右の図のように,底面の対角線の長さが \( 4 \; cm \) で,高さが \( 6 \; cm \) の正四角すいがあります。この正四角すいの体積は何 \( cm^3 \) ですか。
【解説】
正四角すいの底面は正方形になっています。
正方形は「2本の対角線の長さが等しいひし形」ともいえるので,
その面積は,
対角線 \( \times \) 対角線 \( \times \dfrac{1}{2} \)
で求められます。
よって,求める体積は,
\( \left( 4 \times 4 \times \dfrac{1}{2} \right) \times 6 \times \dfrac{1}{3}=16 \; (cm^3) \)
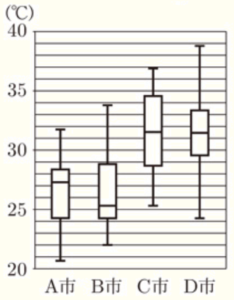
(8) 右の図は,A市,B市,C市,D市について,
ある月の日ごとの最高気温を調べ,その結果を箱ひげ図に表したものです。この月の日ごとの最高気温の四分位範囲が最も大きい市を下のア~エの中から選び,その記号を書きなさい。
ア A市 イ B市 ウ C市 エ D市
【解説】
四分位範囲は,
第三四分位数 \( – \) 第一四分位数
で求めることができます。

各市のおよその四分位範囲は,
A市 ・・・ \( 28.2-24.1=4.1 \)(℃)
B市 ・・・ \( 28.9-24.1=4.7 \)(℃)
C市 ・・・ \( 34.8-28.8=6.0 \)(℃)
D市 ・・・ \( 33.3-29.7=3.6 \)(℃)
大問2
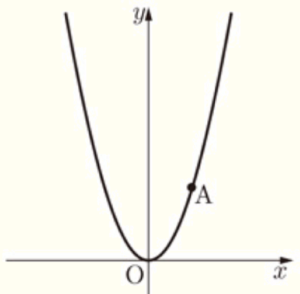
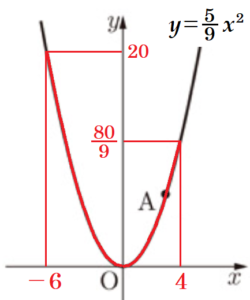
(1) 右の図のように,点 \( A (3,5) \) を通る関数 \( y=ax^2 \) のグラフがあります。この関数について,\( x \) の変域が \( -6≦x≦4 \) のとき,\( y \) の変域を求めなさい。
【解説】
\( y=ax^2 \) に \( x=3,y=5 \) を代入すると,
\( 5=a \times 3^2 \)
\( a=\dfrac{5}{9} \)
なので,このグラフの式は,\( y=\dfrac{5}{9}x^2 \)
また,\( y=ax^2 \;\; (a>0) \) のグラフで,
\( x \) の変域が \( 0 \) を含むとき,\( y \) の変域の最小値は \( 0 \) になります。
\( y \) の変域の最大値については,
\( x \) の絶対値が最も大きくなる時に \( y \) の値は最大値をとります。
\( -6≦x≦4 \) の中で,\( x \) の絶対値が最も大きくなるのは,
\( x=-6 \) のときで,\( y=\dfrac{5}{9} \times (-6)^2=20 \)
以上より,\( y \) の変域は,\( 0≦y≦20 \)
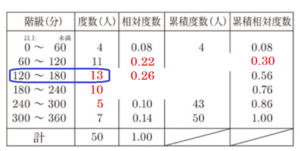
(2) ある中学校の50人の生徒に,平日における1日当たりのスマートフォンの使用時間についてアンケート調査をしました。下の表は,その結果を累積度数と累積相対度数を含めた度数分布表に整理したものです。しかし,この表の一部が汚れてしまい,いくつかの数値が分からなくなっています。この表において,数値が分からなくなっているところを補ったとき,度数が最も多い階級の階級値は何分ですか。
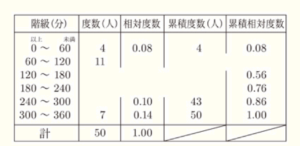
【解説】
順番に空欄を埋めていきます。
60分以上120分未満の階級について,度数が11人なので,
相対度数 \( =11 \div 50=0.22 \)
累積相対度数 \( =0.08+0.22=0.30 \)
120分以上180分未満の階級について,累積相対度数が \( 0.56 \) なので,
相対度数 \( =0.56-0.30=0.26 \)
度数 \( =0.26 \times 50=13 \)(人)
240分以上300分未満の階級について,相対度数が \( 0.10 \) なので,
度数 \( =0.10 \times 50=5 \)(人)
180分以上240分未満の階級について,度数の合計は50人なので,
度数 \( =50-(4+11+13+5+7)=10 \)(人)
よって,度数が最も多い階級は120分以上180分未満の階級なので,
階級値は \( \dfrac{120+180}{2}=150 \)(分)
(3) 2桁の自然数があります。この自然数の十の位の数と一の位の数を入れかえた自然数をつくります。このとき,もとの自然数を4倍した数と,入れかえた自然数を5倍した数の和は,9の倍数になります。このわけを,もとの自然数の十の位の数を \( a \),一の位の数を \( b \) として,\( a \) と \( b \) を使った式を用いて説明しなさい。
【解答】
もとの自然数は \( 10a+b \),これを4倍した数は \( 4(10a+b) \),
十の位の数と一の位の数を入れかえた自然数は \( 10b+a \),これを5倍した数は \( 5(10b+a) \)
と表すことができるので,
もとの自然数を4倍した数と,入れかえた自然数を5倍した数の和は,
\( 4(10a+b)+5(10b+a)=45a+54b \)
\( =9(5a+6b) \)
と表すことができる。
\( a,b \) はともに \( 0 \) 以上 \( 9 \) 以下の整数なので,\( 5a+6b \) も整数であり,
\( 9(5a+6b) \) は9の倍数である。
よって,もとの自然数を4倍した数と,入れかえた自然数を5倍した数の和は,9の倍数になる。
大問3
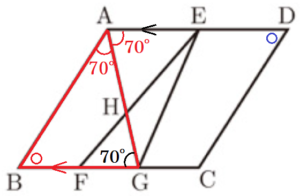
下の図のように,平行四辺形 \( ABCD \) があり,点 \( E \) は辺 \( AD \) の中点です。辺 \( BC \) を3等分する点を,点 \( B \) に近い方から順に \( F,G \) とし,線分 \( AG \) と線分 \( EF \) との交点を \( H \) とします。
次の (1)・(2) に答えなさい。
(1) \( ∠AGB=70°,∠BAG=∠DAG \) となるとき,\( ∠ADC \) の大きさは何度ですか。
【解説】
平行四辺形の向かい合う辺は平行なので,錯角は等しく,
\( ∠AGB=∠DAG=70° \)
\( ∠BAG=∠DAG \) なので,
\( ∠BAG=∠DAG=70° \)
\( △ABG \) において,
\( ∠ABG=180°-(∠AGB+∠DAG)=40° \)
平行四辺形の向かい合う角は等しいので,
\( ∠ADC=∠ABG=40° \)
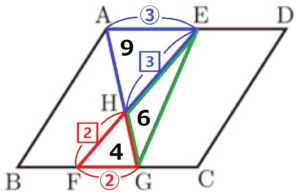
(2) \( △AHE \) の面積が \( 9 \) となるとき,\( △EFG \) の面積を求めなさい。
【解説】
平行四辺形の向かい合う辺の長さは等しいので,
\( AE=\dfrac{1}{2}AD,GF=\dfrac{1}{3}BC \) より,
\( AE:GF=\dfrac{1}{2}AD:\dfrac{1}{3}BC \)
\( =\dfrac{1}{2}AD:\dfrac{1}{3}AD \)
\( =3:2 \)
\( △AHE \) ∽ \( △GHF \),相似比は \( 3:2 \) であり,
相似な三角形の面積比は相似比の2乗の比になるので,
\( △AHE:△GHF=3^2:2^2=9:4 \)
よって,\( △AHE \) の面積が \( 9 \) となるとき,\( △GHF \) の面積は \( 4 \)
また,\( EH:FH=3:2 \) であり,
\( △GHE \) と \( △GHF \) は,高さが共通なので,
底辺の長さの比と面積比が等しくなります。
ここから,
\( △GHE:△GHF=EH:FH \)
\( △GHE:4=3:2 \)
\( △GHE=6 \)
よって,\( △EFG=△GHE+△GHF=10 \)
大問4
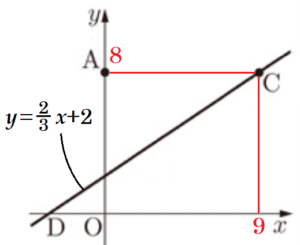
下の図のように,\( y \) 軸上に点 \( A(0,8) \) があり,関数 \( y=\dfrac{2}{3}x+2 \) のグラフ上に,\( x>0 \) の範囲で動く2点 \( B,C \) があります。点 \( C \) の \( x \) 座標は点 \( B \) の \( x \) 座標の4倍です。また,このグラフと \( x \) 軸との交点を \( D \) とします。
次の (1)・(2) に答えなさい。
(1) 線分 \( AC \) が \( x \) 軸に平行となるとき,線分 \( AC \) の長さを求めなさい。
【解説】
点 \( A(0,8) \) なので,
線分 \( AC \) が \( x \) 軸に平行となるとき,
点 \( C \) の \( y \) 座標も \( 8 \) になります。
点 \( C \) は \( y=\dfrac{2}{3}x+2 \) 上の点なので,
\( 8=\dfrac{2}{3}x+2 \)
\( \dfrac{2}{3}x=6 \)
\( x=9 \)
よって,線分 \( AC \) の長さは \( 9 \)
(2) \( DB=BC \) となるとき,直線 \( AC \) の傾きを求めなさい。
【解説】
点 \( B,C \) から \( x \) 軸に垂線をひき,
交点を点 \( P,Q \) とし,点 \( P \) の \( x \) 座標を \( s \) とすると,点 \( Q \) の \( x \) 座標は \( 4s \) と表すことができます。
このとき,\( PQ \) の長さは \( 3s \) となるので,\( DB=BC \) より,\( DP=PQ=3s \) であり,
点 \( D \) の \( x \) 座標は \( -2s \) と表すことができます。
点 \( D \) は \( y=\dfrac{2}{3}x+2 \) 上の点なので,
\( 0=\dfrac{2}{3} \times (-2s)+2 \)
\( \dfrac{4}{3}s=2 \)
\( s=\dfrac{3}{2} \)
\( s=\dfrac{3}{2} \) のとき,
点 \( C \) の \( x \) 座標は \( 4s=4 \times\dfrac{3}{2}=6 \) なので,
\( y \) 座標は \( y=\dfrac{2}{3} \times 6+2=6 \) となります。
よって,
直線 \( AC \) は,\( A(0,8),C(6,6) \) を通るので,
傾き \( =\dfrac{6-8}{6-0}=-\dfrac{1}{3} \)
大問5
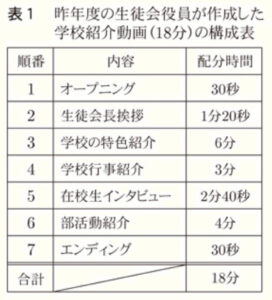
A高校の生徒会役員の中川さんと田村さんは,生徒会を担当する先生からの依頼を受け,長さ \( 15 \) 分の学校紹介動画を作成することになりました。下の表1は,昨年度の生徒会役員が作成した長さ \( 18 \) 分の学校紹介動画の構成表です。2人は,昨年度作成された長さ \( 18 \) 分の学校紹介動画の内容や配分時間を参考にして,長さ \( 15 \) 分の学校紹介動画を作成しようと考えています。
2人は,作成する学校紹介動画が,昨年度の生徒会役員が作成したものよりも時間が短くなることを踏まえ,下のように【学校紹介動画(\( 15 \) 分)の作成方針】を決めました。
【学校紹介動画 (\( 15 \) 分) の作成方針】
(Ⅰ) オープニング,学校の特色紹介,学校行事紹介,エンディングの配分時間は,昨年度の生徒会役員が
作成した学校紹介動画と同じにする。
(Ⅱ) 生徒会長挨拶は動画の内容に入れない。
(Ⅲ) 在校生インタビューでは,配分時間を代表生徒3人に均等に割り当てる。
(Ⅳ) 部活動紹介では,配分時間のうち \( 30 \) 秒を,A高校にどのような部活動があるかについての紹介に
割り当てる。また,部活動紹介の配分時間の残りを,A高校にある部活動のうち代表の部活動3つに
均等に割り当てる。
(Ⅴ) 部活動紹介における代表の部活動1つに割り当てる時間は,在校生インタビューにおける代表生徒1人に
割り当てる時間の \( 1.5 \) 倍にする。
2人は【学校紹介動画 (\( 15 \) 分) の作成方針】に従って構成表を作り,学校紹介動画を作成することにしました。
次の (1)・(2) に答えなさい。
(1) 在校生インタビューにおける代表生徒3人のうち1人は,生徒会長に決まりました。残りの代表生徒2人を校内で募集したところ,Pさん,Qさん,Rさん,Sさん,Tさんの5人が立候補しました。この5人の中から,くじ引きで2人を選ぶとき,Pさんが選ばれる確率を求めなさい。
【解説】
Pさん,Qさん,Rさん,Sさん,Tさんから2人選ぶ組み合わせを樹形図として書き,
Pさんが選ばれる組み合わせのところに
○ をつけます。
Pさんが選ばれる組み合わせは4通り,すべての組み合わせは10通りなので,
求める確率は,\( \dfrac{4}{10}=\dfrac{2}{5} \)
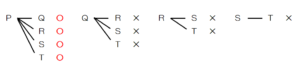
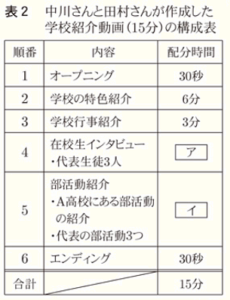
(2) 下の表2は,中川さんと田村さんが【学校紹介動画(\( 15 \) 分)の作成方針】に従って作成した長さ \( 15 \) 分の学校紹介動画の構成表です。
表2の \( \fbox{ ア } \)・ \( \fbox{ イ } \) に当てはまる配分時間をそれぞれ求めなさい。なお,答えを求める過程も分かるように書きなさい。
【解答】
在校生インタビュー全体に割り当てられる時間を \( x \) 秒,
部活動紹介全体に割り当てられる時間は,\( y \) 秒とすると,
これらの時間の合計は,\( 15-(0.5+6+3+0.5)=5 \)(分)つまり,\( 300 \) 秒なので,
\( \left\{ \begin{array}{}
x+y=300 \;\; ・・・ \; ➀ \\
1.5 \times \dfrac{x}{3}=\dfrac{y-30}{3} \;\; ・・・ \; ➁ \\
\end{array} \right. \)
➁を整理すると,
\( 1.5x-y=-30 \) ・・・ ➁’
➀\( + \)➁’すると,
\( 2.5x=270 \)
\( x=108 \)
➀に代入すると,
\( 108+y=300 \)
\( y=192 \)
よって,
在校生インタビュー全体に割り当てられる時間は,\( 108 \) 秒,
つまり, \( 1 \) 分 \( 48 \) 秒
部活動紹介全体に割り当てられる時間は,\( 192 \) 秒,
つまり, \( 3 \) 分 \( 12 \) 秒
大問6
中村さんは,ある数学の本に掲載されていた下の【問題】に興味をもち,この【問題】について考えることにしました。
【問題】
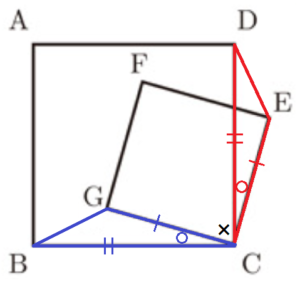
右の図のように,1つの平面上に大きさの異なる正方形 \( ABCD \) と正方形 \( CEFG \) があり,点 \( F \) と点 \( G \) が正方形 \( ABCD \) の内部にあります。7つの点 \( A,B,C,D,E,F,G \) から2点を選び,その2点を結んでできる線分の中で,線分 \( DE \) と長さが同じであるものを答えなさい。
中村さんは,下のことを予想しました。
【予想】
1つの平面上に大きさの異なる正方形 \( ABCD \) と正方形 \( CEFG \) があり,
点 \( F \) と点 \( G \) が正方形 \( ABCD \) の内部にあるとき,\( DE=BG \) である。
次の (1)・(2) に答えなさい。
(1) 中村さんは,下のように \( △CED≡△CGB \) を示し,それを基にして,この【予想】が成り立つことを証明しました。
【中村さんの証明】
\( △CED \) と \( △CGB \) において
ア
合同な図形の対応する辺は等しいから
\( DE=BG \)
【中村さんの証明】の ア に証明の続きを書き,証明を完成させなさい。
【解答】
正方形 \( CEFG \) の辺の長さはすべて等しいので,
\( CE=CG \) ・・・ ➀
正方形 \( ABCD \) の辺の長さはすべて等しいので,
\( CD=CB \) ・・・ ➁
正方形の4つの角はすべて \( 90° \) なので,
\( ∠ECG=∠DCB=90° \) であり,
\( ∠ECD=∠ECG-∠DCG=90°-∠DCG \) ・・・ ➂
\( ∠GCB=∠DCB-∠DCG=90°-∠DCG \) ・・・ ➃
➂➃より,
\( ∠ECD=∠GCB \) ・・・ ➄
➀➁➄より,2組の辺とその間の角がそれぞれ等しいので,
\( △CED≡△CGB \)
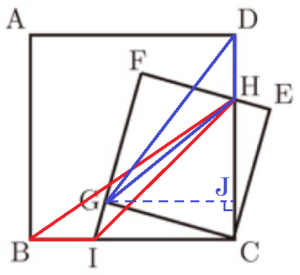
中村さんは,【問題】中の図で辺 \( CD \) と辺 \( EF \) との交点を \( H \) としたとき,線分 \( CH \) と長さが同じである線分がないか考えることにしました。そこで,\( △CEH \) に着目し,この三角形と合同な三角形を見つけるために辺 \( FG \) を延長し,辺 \( FG \) の延長と辺 \( BC \) との交点を \( I \) とした下のような図をかきました。中村さんは,自分がかいた図について,\( △CEH≡△CGI \) であることがいえるので,それを基にして,\( CH=CI \) であることが分かりました。
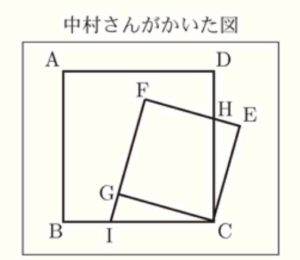
さらに,中村さんは,自分がかいた図について,\( CH=CI \) 以外にも成り立つことがらがあるのではないかと考えました。
(2) 下のア~オのことがらの中で,中村さんがかいた図について成り立つことがらを全て選び,その記号を書きなさい。
ア 四角形 \( AICH \) はひし形である。
イ 四角形 \( AICH \) の面積は,三角形 \( CDI \) の面積の2倍である。
ウ 線分 \( BD \) と線分 \( IH \) は平行である。
エ \( △BIH≡△DHG \) である。
オ 4点 \( C,H,F,I \) は1つの円周上にある。
【解説】
ア \( △ADH \) において,線分 \( AH \) は斜辺なので,\( AH>AD \)
また,\( CH<CD \) なので,\( AD=CD \) より,\( AH>CH \)
よって,四角形 \( AICH \) はひし形ではありません。
イ \( DH=BI,AD=AB,∠ADH=∠ABI \)なので,
\( △ADH≡△ABI \)
また,\( △ABC=\dfrac{1}{2} \)正方形 \( ABCD \) なので,
\( △ACI=\dfrac{1}{2} \)四角形 \( AICH \)
正方形の向かい合う辺は平行なので,\( AD//BC \) であり,
等積変形の考え方から,\( △ACI=△CDI \)
よって,\( △CDI=\dfrac{1}{2} \)四角形 \( AICH \)
ウ \( CD=BC,CH=CI,∠C=90° \)(共通)より,
\( △BCD \) と \( △CHI \) はともに直角二等辺三角形になっています。
よって,\( ∠DBC=∠HIC=45° \) で,同位角が等しいので,
\( BD//IH \)
エ \( △BIH=BI \times CH \times \dfrac{1}{2} \)
\( △DHI=DH \times CH \times \dfrac{1}{2} \)
なので,\( BI=DH,CH=CI \) より,\( △BIH=△DHI \)
点 \( G \) から辺 \( CD \) に垂線をひき,交点を \( J \) とすると,
\( CI>GJ \) なので,\( △DHI>△DHG \)
よって,\( △BIH>△DHG \) であり,
面積が等しくない三角形は合同ではありません。
オ 線分 \( HI \) を直径とすると,\( ∠IFH,∠ICH \) は,
直径 \( HI \) に対する円周角であり,どちらも \( 90° \) なので,
4点 \( C,H,F,I \) は1つの円周上にある。










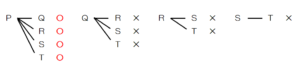




-アイキャッチ-120x68.jpg)