大問1
(1) \( 4-11 \)
(2) \( (-10) \div \dfrac{2}{5} \)
【解説】
\( =(-10) \times \dfrac{5}{2} \)
\( =-25 \)
(3) \( (-2.3)+4.1 \) (小数で答えなさい)
(4) \( 3\sqrt{6} \div \sqrt{2} \)
【解説】
\( =3\sqrt{6} \times \dfrac{1}{\sqrt{2}} \)
\( =3\sqrt{3} \)
(5) \( 3a \times (-2b)^2 \)
【解説】
\( =3a \times 4b^2 \)
\( =12ab^2 \)
(6) \( -(5x-y)+2(x+2y) \)
【解説】
\( =-5x+y+2x+4y \)
\( =-3x+5y \)
大問2
(1) 一次方程式 \( 5x-2=3x+4 \) の解は,\( x= \) である。
【解説】
\( 5x-2=3x+4 \)
\( 5x-3x=4+2 \)
\( 2x=6 \)
\( x=3 \)
(2) 連立方程式 \( \left\{ \begin{array}{}
3x+2y=-2 \\
x-y=6 \\
\end{array} \right. \) の解は,\( x= \) ,\( y= \) である。
【解説】
\( \left\{ \begin{array}{}
3x+2y=-2 \;\; ・・・ \;\; ➀ \\
x-y=6 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁ \( \times 2 \) すると,
\( 2x-2y=12 \) ・・・ ➁’
➀ \( + \) ➁ すると
\( 5x=10 \)
\( x=2 \)
➁に代入すると,
\( 2-y=6 \)
\( y=-4 \)
(3) \( (x-2y)(x+2y) \) を展開して整理すると, である。
【解説】
\( (x-2y)(x+2y)=x^2-4y^2 \)
(4) \( 3ax^2-2ax \) を因数分解すると, である。
【解説】
\( 3ax^2-2ax=ax(3x-2) \)
(5) 二次方程式 \( 3x^2-5x+1=0 \) の解は,\( x= \) である。
【解答】
\( x=\dfrac{5±\sqrt{13}}{6} \)
【解説】
解の公式より,
\( x=\dfrac{-(-5)±\sqrt{(-5)^2-4 \times 3 \times 1}}{2 \times 3} \)
\( =\dfrac{5±\sqrt{25-12}}{6} \)
\( =\dfrac{5±\sqrt{13}}{6} \)
(6) \( \sqrt{2} \) と \( \dfrac{3}{2} \) の大小関係を式で表すと, である。次のア~ウのうちから1つ選び,記号で答えなさい。
ア \( \sqrt{2}=\dfrac{3}{2} \) イ \( \sqrt{2}<\dfrac{3}{2} \) ウ \( \sqrt{2}>\dfrac{3}{2} \)
【解答】
イ \( \sqrt{2}<\dfrac{3}{2} \)
【解説】
2つの正の数 \( a,b \) について,\( a<b \) であるとき,\( a^2<b^2 \) になります。
\( \sqrt{2} \) と \( \dfrac{3}{2} \) の2つの正の数について,
\( (\sqrt{2})^2=2.\left( \dfrac{3}{2} \right)^2=\dfrac{9}{4} \) なので,
\( 2<\dfrac{9}{4} \) より,\( \sqrt{2}<\dfrac{3}{2} \) になります。
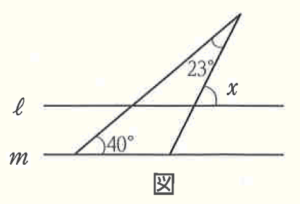
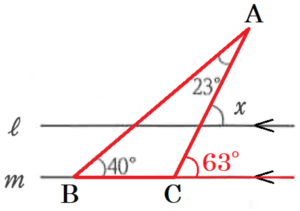
(7) 右の図において,ℓ\( //m \) のとき,
\( ∠x= \) \( ° \) である。
【解説】
右の図のように3点に \( A,B,C \) と名前を
つけると,\( △ABC \) の外角は
\( 40°+23°=63° \)
であり,ℓ\( //m \) より,同位角は等しいので,
\( ∠x=63° \)
(8) ある中学校の生徒6人が砲丸投げを行ったところ,下のような結果になった。この6人の砲丸投げの記録の中央値は, \( m \) である。
[記録] \( \boxed{ 8,7,4,5,4,9 \;\;\;\; (m) } \)
【解説】
記録を小さい順に並べ替えると,
\( 4,4,5,7,8,9 \)
になります。
全部で6人の記録の中央値は小さい方から3番目と4番目の値の平均値になるので,
中央値は,\( \dfrac{5+7}{2}=6 \; (m) \) になります。
(9) あるアルミ工場で製造した製品から \( 200 \) 個を無作為に抽出して検査をすると,不良品の割合が \( 0.03 \) と推定された。この工場で製造された製品 \( 8000 \) 個に含まれる不良品は,およそ 個であると推定される。次のア~エのうちから1つ選び,記号で答えなさい。
ア \( 240 \) イ \( 600 \) ウ \( 1200 \) エ \( 2400 \)
【解説】
母集団(\( 8000 \) 個)に含まれる不良品の割合と抽出した標本(\( 200 \) 個)に含まれる不良品の割合は等しくなると考えられます。
つまり,製造された製品 \( 8000 \) 個に含まれる不良品の割合も \( 0.03 \) なので,
\( 8000 \) 個中に含まれる不良品の個数は,
\( 8000 \times 0.03=240 \)(個)
になります。
大問3
下の図は,2017年度,2018年度,2022年度,2023年度について,沖縄県入域観光客数(国内)の月ごとの人数をそれぞれ12か月分調べ,箱ひげ図にまとめたものである。
ただし,沖縄県入域観光客数(国内)とは,沖縄県在住者を除く,沖縄県を訪れた国内客の人数のことである。また,月ごとの人数は千の位を四捨五入しており,単位は万人である。
このとき,次の各問いに答えなさい。

問1 2018年度のデータについて,第3四分位数を答えなさい。
【解説】
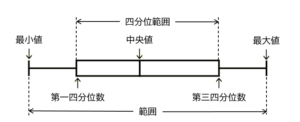
第3四分位数を表すのは箱の右端部分にあたる値です。
問2 図から読み取れることとして,必ず正しいといえるものを,次のア~エのうちから1つ選び,記号で答えなさい。
ア 2017年度よりも2018年度の方が,データの四分位範囲が大きい。
イ 4つの年度のうち,データの平均値が最も大きいのは,2018年度である。
ウ 沖縄県入域観光客数 (国内) が \( 52 \) 万人以下の月は,2022年度よりも2018年度の方が
多い。
エ 2023年度において,沖縄県入域観光客数 (国内)が \( 60 \) 万人以上の月は,6か月以上ある。
【解説】
ア ・・・ 四分位範囲は箱の長さで表され,四分位範囲が大きいほど箱の長さが長くなります。
つまり,箱の長さが長い2017年の方が四分位範囲が大きいことになります。
イ ・・・ 箱ひげ図のデータだけでは平均値はわかりません。
ウ ・・・ 2018年度の箱ひげ図では,第1四分位数は \( 52 \) 万人より大きい値になっており,
第1四分位数は少ない方から3番目と4番目の値の平均値になることから,
4番目の値は必ず \( 52 \) 万人より大きい値になります。
(2つの値とその平均値との関係については別途解説あり)
ここから,\( \color{red}{52} \) 万人以下の月は,3か月以下であったことがわかります。
2022年度の箱ひげ図では,第1四分位数は \( 52 \) 万人より小さい値になっていることから,
3番目の値は必ず \( 52 \) 万人より小さい値になります。
ここから,\( \color{red}{52} \) 万人以下の月は,3か月以上であったことがわかります。
よって,正しくありません。
エ ・・・ 2022年度の箱ひげ図では,中央値は \( 60 \) 万人であり,中央値は少ない方から
6番目と7番目の値の平均値になることから,7番目の値は必ず \( 60 \) 万人以上の値になります。
ここから,\( 60 \) 万人以上の月は6か月以上であったとわかります。
2つの数A,Bと平均値の関係
2つの数 \( A,B \;(A≦B) \) の平均値が
\( 53 \) であるとき,\( A,B \) がどのような数になるのか考えてみます。
【\( A=B \) のとき】
\( \dfrac{A+B}{2}=53 \) なので,
\( \dfrac{A+B}{2}=53 \)
\( \dfrac{A+A}{2}=53 \)
\( A=53 \)
よって,\( A=B \) であるとき,\( A,B \) はどちらも平均値と一致します。
【\( A<B \) の場合】
\( A \) の値について
\( \dfrac{A+B}{2}=53 \) なので,
\( B=A+x \; (x>0) \) とすると,
\( \dfrac{A+(A+x)}{2}=53 \)
\( \dfrac{2A+x}{2}=53 \)
\( A=53-\dfrac{x}{2} \)
よって,\( A<B \) であるとき,
\( A \) の値は平均値より小さい値になります。
\( \phantom{あああ} \)
\( B \) の値について
\( \dfrac{A+B}{2}=53 \) なので,
\( A=B-x \; (x>0) \) とすると,
\( \dfrac{(B-x)+B}{2}=53 \)
\( \dfrac{2B-x}{2}=53 \)
\( B=53+\dfrac{x}{2} \)
よって,\( A<B \) であるとき,
\( B \) の値は平均値より大きい値になります。
これらをまとめると,
2つの数 \( A,B \;(A≦B) \) とその平均値の関係は
\( A \) の値は必ず平均値以下,\( B \) の値は必ず平均値以上
になります。
問3 2023年度の箱ひげ図と同じデータを使ってまとめたヒストグラムとして最も適するものを,次のア~エのうちから1つ選び,記号で答えなさい。なお,\( 50 \) 万人以上 \( 52 \) 万人未満,\( 52 \) 万人以上 \( 54 \) 万人未満のように,階級の幅はいずれも \( 2 \) 万人である。
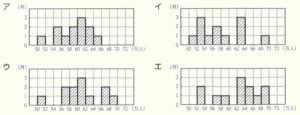
【解説】
箱ひげ図から,最小値は約 \( 51 \) 万人で,\( 50 \) 万人以上 \( 52 \) 万人未満の階級に含まれているので,
\( 50 \) 万人以上 \( 52 \) 万人未満の階級の度数が \( 0 \) である
エのヒストグラムはあてはまりません。
最大値は約 \( 68 \) 万人で,\( 68 \) 万人以上 \( 70 \) 万人未満の階級に含まれているので,
\( 68 \) 万人以上 \( 70 \) 万人未満の階級の度数が \( 0 \) であるアのヒストグラムはあてはまりません。
第1四分位数は約 \( 57 \) 万 \( 5 \) 千人で,\( 56 \) 万人以上 \( 58 \) 万人未満の階級に含まれています。
第1四分位数は少ない方から3番目と4番目の値の平均値であり,イのヒストグラムでは,
少ない方から3番目と4番目の値はどちらも \( 52 \) 万人以上 \( 54 \) 万人未満の階級に含まれています。
ここから,平均値も \( 52 \) 万人以上 \( 54 \) 万人未満の階級に含まれることになるので,あてはまりません。
よって,最も適するヒストグラムはウになります。
大問4
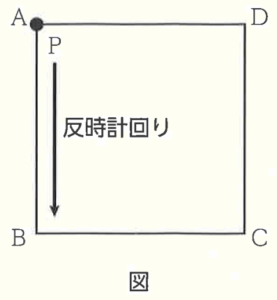
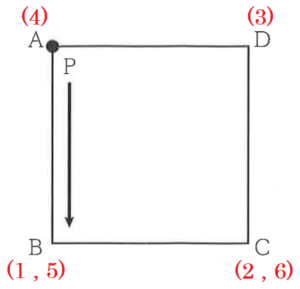
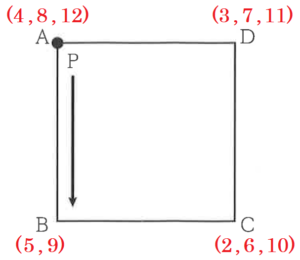
右の図のような正方形 \( ABCD \) がある。点 \( P \) は最初,頂点 \( A \) の位置にあり,1つのさいころを投げて,次の規則にしたがって移動する。
規則1 出た目の数だけ正方形の辺に沿って,
反時計回りに頂点を1つずつ移動する。
規則2 さいころを2回投げるときは,1回目に
移動した場所から,続けて反時計回りに
移動する。
例えば,さいころを2回投げるとき,1回目に \( 1 \) の目が出たら,点 \( P \) は頂点 \( A \) から頂点 \( B \) に移動し,さらに2回目に \( 2 \) の目が出たら,点 \( P \) は頂点 \( B \) から頂点 \( C \) を通って頂点 \( D \) に移動する。
このとき,次の各問いに答えなさい。
ただし,さいころはどの目が出ることも同様に確からしいものとする。
問1 さいころを1回投げて,点 \( P \) が頂点 \( D \) の位置にある確率を求めなさい。
【解説】
さいころの出た目と点 \( P \) が移動する頂点の関係を
表すと右の図のようになります。
点 \( P \) が頂点 \( D \) の位置に移動するのは,
\( 3 \) の目が出たときなので,
その確率は \( \dfrac{1}{6}\) になります。
問2 さいころを1回投げて,点 \( P \) が頂点 \( B \) の位置にある確率を求めなさい。
【解説】
点 \( P \) が頂点 \( B \) の位置に移動するのは,
\( 1 \) か \( 5 \) の目が出たときなので,
その確率は \( \dfrac{2}{6}=\dfrac{1}{3} \) になります。
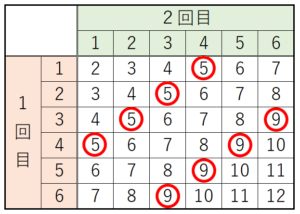
問3 さいころを2回投げて,点 \( P \) が頂点 \( B \) の位置にある確率を求めなさい。
【解説】
さいころを2回投げて出た目の和と点 \( P \) が
移動する頂点の関係を表すと右の図のようになり,
頂点 \( B \) の位置に移動するのは,
2つの和が \( 5 \) か \( 9 \) になるときです。
さいころを2回投げて出た目の組み合わせと
その和について表に書き出し,和が \( 5 \) または \( 9 \) に
なるところに ○ をつけてみます。
和が \( 5 \) または \( 9 \) になる組み合わせは \( 8 \) 通り,
全ての組み合わせは \( 36 \) 通りなので,
求める確率は \( \dfrac{8}{36}=\dfrac{2}{9} \) になります。
大問5
下の図は,学校の体育館でシートの上に椅子を並べている様子である。椅子の前脚から後脚までの幅は \( 50 \; cm \) であり,椅子と椅子の間隔を \( a \; cm \) 空けて規則的に椅子を並べていく。はじめにシートの先端から \( 10 \; cm \) 空けて最初の椅子を置き,最後の椅子を置いたときに,椅子の後脚がちょうどシートの端にくるように,椅子を並べるものとする。
このとき,次の各問いに答えなさい。
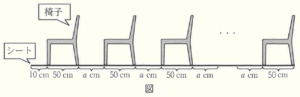
問1 下の表は,\( a=40 \) のときの椅子の数と椅子を並べるのに必要なシートの長さの関係を示した表の一部である。
このとき,下の表の \( \boxed{ } \) にあてはまる最も適する数を答えなさい。

【解説】

前の椅子の後脚から次の椅子の後脚までの距離は \( 40+50=90 \; (cm) \) になるので,
椅子を \( 3 \) 脚並べるのに必要なシートの長さは \( 150+90=240 \; (cm) \)
椅子を \( 4 \) 脚並べるのに必要なシートの長さは \( 240+90=330 \; (cm) \)
になります。
問2 \( a=40 \) とする。椅子の数を \( x \) 脚,椅子を並べるのに必要なシートの長さを \( y \; cm \) としたとき,\( y \) を \( x \) の式で表しなさい。
【解説】
求める式を \( y=mx+n \) とすると,
シートの長さは \( 90 \; cm \) ずつ長くなっているので,
傾き \( m=90 \) になります。
次に,表から,\( x=1 \) のとき,\( y=60 \) なので,
\( y=90x+n \) に代入すると,
\( 60=90 \times 1+n \)
\( 60=90+n \)
\( n=-30 \)
よって,求める式は \( y=90x-30 \)
問3 長さ \( 3180 \; cm \) のシートに \( 40 \) 脚の椅子を並べるとき,\( a \) の値を求めなさい。
【解説】
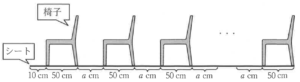
図から,椅子の数を増やしていったときの必要なシートの長さを表にして書き出すと,

となり,必要なシートの長さは,
椅子が \( 2 \) 脚のとき ・・・ \( 60+(a+50) \times 1 \; (cm) \)
椅子が \( 3 \) 脚のとき ・・・ \( 60+(a+50) \times 2 \; (cm) \)
椅子が \( 4 \) 脚のとき ・・・ \( 60+(a+50) \times 3 \; (cm) \)
・・・
椅子が \( 40 \) 脚のとき ・・・ \( 60+(a+50) \times 39 \; (cm) \)
となります。
よって,\( 40 \) 脚の椅子を並べるときに必要なシートの長さが \( 3180 \; cm \) であるとき,
\( 60+(a+50) \times 39=3180 \)
\( (a+50) \times 39=3120 \)
\( a+50=80 \)
\( a=30 \)
大問6
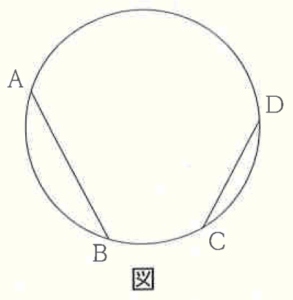
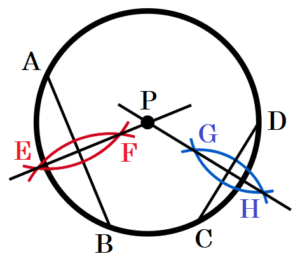
右の図のように,円周上に4点 \( A,B,C,D \) がある。弦 \( AB \),弦 \( CD \) を利用して,円の中心 \( P \) を定規とコンパスを使って作図しなさい。
ただし,円の中心を示す記号 \( P \) をかき入れ,作図に用いた線は消さずに残しておくこと。
【解答】
手順1 2点 \( A,B \) を中心に円弧を描く。
(交点を \( E,F \) とします)
手順2 2点 \( E,F \) を通る直線を描く。
手順3 2点 \( C,D \) を中心に円弧を描く。
(交点を \( G,H \) とします)
手順4 2点 \( G,H \) を通る直線を描く。
手順2と手順4の直線の交点が,求める点 \( P \) になります。
【解説】
円の中心から弦に対して垂線をひくと,弦を二等分します。
この逆を考えると,ある弦の垂直二等分線をひくと,必ず円の中心を通ります。
つまり,2本の弦に対して垂直二等分線をひいた交点が円の中心になります。
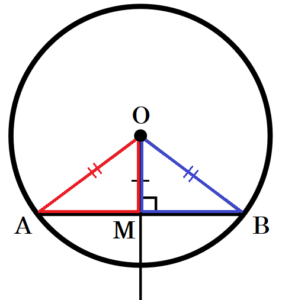
円の中心から弦にひいた垂線が垂直二等分線になる理由
円 \( O \) の中心から弦 \( AB \) に垂線をひいた
交点を \( M \) とすると,
\( △OAM \) と \( △OBM \) において,
円 \( O \) の半径なので,\( OA=OB \) ・・・ ➀
仮定より,\( ∠OMA=∠OMB=90° \) ・・・ ➁
\( OM \) は共通 ・・・ ➂
➀➁➂より,直角三角形において
斜辺と他の1辺がそれぞれ等しいので,
\( △OAM≡△OBM \)
合同な三角形の対応する辺は等しいので,\( AM=BM \) であり,
店 \( M \) は弦 \( AB \) の中点になっています。
よって,直線 \( OM \) は弦 \( AB \) の中点を通る垂線なので,垂直二等分線であるといえます。
大問7
雄太さんと桃子さんは,次の【宿題】について考えた。下の【会話】は,2人が話し合っている場面である。
【宿題】
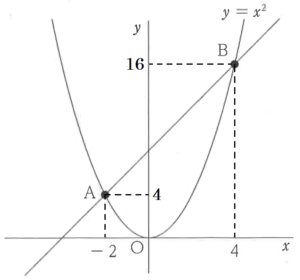
右の図のように,関数 \( y=x^2 \) のグラフ上に \( x \) 座標が \( -2 \) である点 \( A \) と,\( x \) 座標が \( 4 \) である点 \( B \) がある。\( y \) 軸上に \( y \) 座標が \( 2 \) である点 \( C \) をとったときの,\( △ABC \) の面積を求めなさい。
また,\( △ABC \) と \( △ABP \) の面積が等しくなるような点 \( P \) を \( x \) 軸上にとるとき,点 \( P \) の座標を求めなさい。
ただし,原点 \( O \) から点 \( (0,1) \),点 \( (1,0) \) までの長さをそれぞれ \( 1 \; cm \) とする。
\( \phantom{ } \)
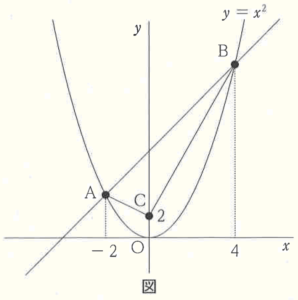
【会話】
雄太:点 \( A \) の座標は \( A(-2, \) ア \( ) \) になるね。同じように点 \( B \) の座標もわかるね。
桃子:2点の座標がわかったから,2点 \( A,B \) を通る直線の式が,\( y= \) イ であることが
求められたよ。
雄太:直線の式がわかったから,\( △ABC \) の面積が ウ \( cm^2 \) になることがわかるね。
桃子:点 \( P \) の座標を求めるためには \( △ABC \) の底辺を線分 \( AB \) としたときに,\( △ABC \) の高さと
\( △ABP \) の高さが同じになるような点 \( P \) を \( x \) 軸上にとればよさそうだね。
雄太:点 \( C \) を通り直線 \( AB \) と平行な直線を使えば,点 \( P \) の座標が求められるね。
桃子:そうだね。点 \( C \) のほかにも \( y \) 軸上に点 \( D \) をとって,\( △ABC \) の面積と \( △ABD \) の面積が
等しくなるようにできるね。点 \( D \) を通り直線 \( AB \) と平行な直線を利用することでも
問題の条件を満たす点 \( P \) が \( x \) 軸上にとれるから,宿題の答えとなる点 \( P \) は2点あるという
ことだね。
このとき,次の各問いに答えなさい。
問1 ア にあてはまる最も適する数を答えなさい。
【解説】
点 \( A \) は,\( y=x^2 \) 上の点で,\( x \) 座標は \( -2 \) なので,
\( y \) 座標の値は,
\( y=(-2)^2=4 \)
問2 イ にあてはまる最も適する式を答えなさい。
【解説】
点 \( A \) は,\( y=x^2 \) 上の点で,
\( x \) 座標は \( 4 \) なので,
\( y \) 座標の値は,
\( y=4^2=16 \)
求める直線の式を \( y=ax+b \) とすると,
\( A(-2,4),B(4,16) \) を通るので,
\( a=\dfrac{16-4}{4-(-2)}=2 \)
\( y=2x+b \) に \( x=4,y=16 \) を代入すると,
\( 16=2 \times 4+b \)
\( b=8 \)
よって,求める直線の式は \( y=2x+8 \)
問3 ウ にあてはまる最も適する数を答えなさい。
【解説】
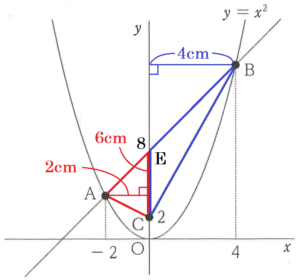
直線 \( AB \) と \( y \) 軸の交点を \( E \) とすると,
\( △ABC=△ACE+△BCE \)
と考えることができます。
\( △ACE \) と \( △BCE \) の底辺を \( CE \) とすると,
\( C,E \) の座標は \( C(0,2),E(0,8) \)
なので, \( CE=6 \; cm \)
\( △ACE \) の高さは,点 \( A \) の \( x \) 座標の絶対値
と等しいので,\( △ACE \) の高さは,\( 2 \; cm \)
\( △BCE \) の高さは,点 \( B \) の \( x \) 座標の絶対値
と等しいので,\( △BCE \) の高さは,\( 4 \; cm \)
になっています。
よって,\( △ABC \) の面積は,
\( △ABC=△ACE+△BCE \)
\( =6 \times 2 \times \dfrac{1}{2}+6 \times 4 \times \dfrac{1}{2} \)
\( =6+12 \)
\( =18 \; (cm^2) \)
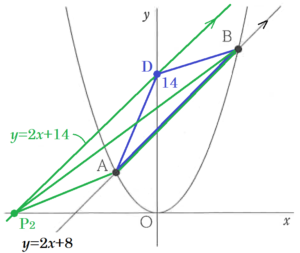
問4 \( △ABC \) と \( △ABP \) の面積が等しくなるような \( x \) 軸上の点 \( P \) の座標を2つ求めなさい。
【解説】
あてはまる \( △ABP \) は直線 \( AB \) の上と下に1個ずつできます。
【直線 \( AB \) の下の場合】
点 \( C \) を通り,直線 \( AB \) と平行な直線と \( x \) 軸の交点を \( P_1 \) とします。
直線 \( CP_1 \) は,\( C(0、2) \) を通り,
直線 \( AB \; (y=2x+8) \) と平行なので,
直線 \( CP_1 \) の式は \( y=2x+2 \) になります,
\( P_1 \) は,\( x \) 軸上の点なので,
\( y=0 \) を代入すると,
\( 0=2x+2 \)
\( x=-1 \)
\( \phantom{ } \)
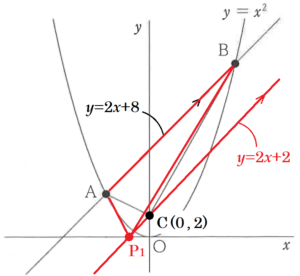
よって,1つ目の点 \( P \) の座標は \( (-1,0) \) になります。
【直線 \( AB \) の上の場合】
まず,\( △ABC \) と \( △ABD \) の面積が等しくなるような \( y \) 軸上の点 \( D \) の座標を求めます。
\( △ABC=△ACE+△BCE \)
\( △ABD=△ADE+△BDE \)
と考えると,\( △ABC=△ABD \) のとき,\( △ACE=△ADE,△BCE=△BDE \) になります。
\( \phantom{ } \)
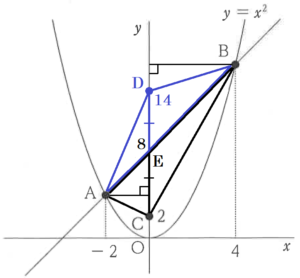
\( △ACE \) と \( △BCE \) の底辺を \( CE \),\( △ADE \) と \( △BDE \) の底辺を \( DE \) とすると、
\( △ACE \) と \( △ADE \),\( △BCE \) と \( △BDE \) は,それぞれ高さが共通なので,
\( CE=DE \) のとき,
\( △ACE=△ADE,△BCE=△BDE \)
になります。
\( CE=6 \; cm \) であることから,\( DE \) も \( 6 \; cm \) であればいいので,
点 \( D \) の座標は \( D(0,14) \) になります。
点 \( D \) を通り,直線 \( AB \) と平行な直線と \( x \) 軸の交点を \( P_2 \) とします。
直線 \( DP_2 \) は,\( D(0,14) \) を通り,
直線 \( AB \; (y=2x+8) \) と平行なので,
直線 \( CP_1 \) の式は \( y=2x+14 \) になります,
\( P_2 \) は,\( x \) 軸上の点なので,
\( y=0 \) を代入すると,
\( 0=2x+14 \)
\( x=-7 \)
よって,2つ目の点 \( P \) の座標は \( (-7,0) \) になります。
大問8
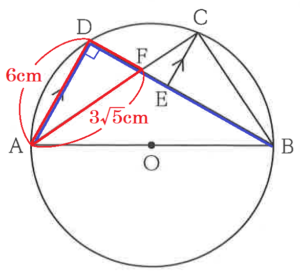
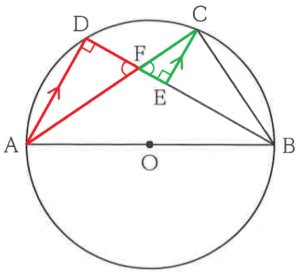
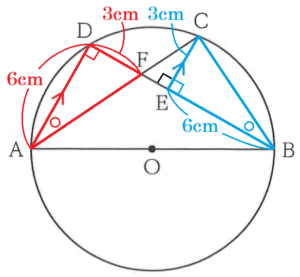
下の図のように,4点 \( A,B,C,D \) を円 \( O \) の円周上にとる。線分 \( AB \) は円 \( O \) の直径であり,線分 \( BD \) 上に \( AD//EC \) となる点 \( E \) をとり,線分 \( AC \) と線分 \( BD \) の交点を \( F \) とする。
また,\( AD=6 \; cm,AF=3\sqrt{5} \; cm,BE=6 \; cm \) とする。
このとき,次の各問いに答えなさい。
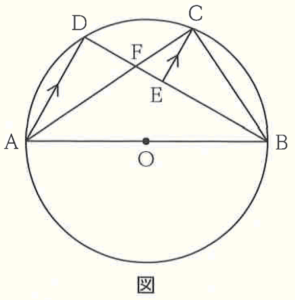
問1 線分 \( DF \) の長さを求めなさい。
【解説】
\( △ADF \) において,
\( ∠ADF \) は 直径に対する円周角なので,
\( ∠ADF=90° \)
であり,\( △ADF \) は直角三角形です。
三平方の定理より,
\( DF^2=(3\sqrt{5})^2-6^2=9 \)
\( DF=3 \; (cm) \) (\( DF>0 \) より)
問2 \( △ADF \) ∽ \( △CEF \) となることを証明しなさい。
【解答】
\( △ADF \) と \( △CEF \) において,
対頂角は等しいので,
\( ∠AFD=∠CFE \) ・・・ ➀
\( AD//EC \) より,錯角は等しいので,
\( ∠ADF=∠CEF=90° \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △ADF \) ∽ \( △CEF \)
問3 \( △ABD \) の面積を求めなさい。
【解答】
\( \dfrac{63}{2} \; cm^2 \)
【解説】
\( ∠ADB=90° \) であることから,\( △ABD \) は直角三角形です。
\( AD=6 \; cm,BE=6 \; cm,DF=3 \; cm \) より,\( EF \) の長さがわかれば,
\( △ABD \) の面積を求めることができます。
\( △ADF \) と \( △BEC \) において,
\( ∠BEC=180°-∠CEF \)
\( =180°-90° \)
\( =90° \)
なので,\( ∠ADF=∠BEC=90° \) ・・・ ➀
\( \stackrel{\huge\frown}{ CD } \) に対する円周角なので,
\( ∠DAF=∠EBC \) ・・・ ➁
仮定より,\( AD=BE=6 \; cm \) ・・・ ➂
➀➁➂より,
1組の辺とその両端の角がそれぞれ等しいので,
\( △ADF≡△BEC \)
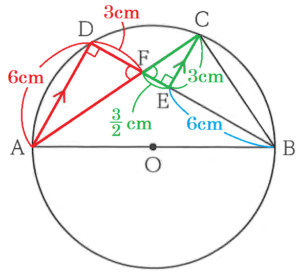
対応する辺は等しいので,\( EC=DF=3 \; (cm) \)
\( △ADF \) と \( △CEF \) において,
問2より,\( △ADF \) ∽ \( △CEF \) なので,
対応する辺の比は等しいので,
\( DF:EF=AD:CE \)
\( 3:EF=6:3 \)
\( EF=\dfrac{3}{2} \; (cm) \)
ここから,線分 \( BD \) の長さは,
\( BD=6+\dfrac{3}{2}+3=\dfrac{21}{2} \; (cm) \)
以上より,\( △ABD \) の面積は,
\( △ABD=6 \times \dfrac{21}{2} \times \dfrac{1}{2}=\dfrac{63}{2} \; (cm^2) \)
大問9
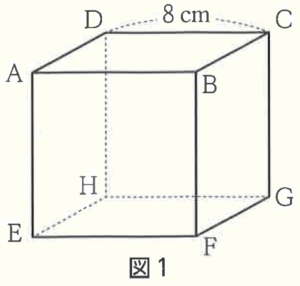
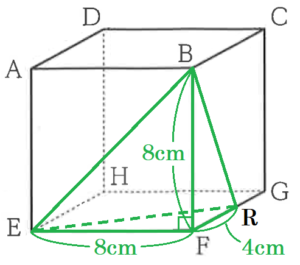
右の図1のように,1辺が \( 8 \; cm \) の立方体 \( ABCD-EFGH \) がある。
このとき,次の各問いに答えなさい。
問1 図1の立方体の体積を求めなさい。
【解説】
\( 8 \times 8 \times 8=512 \; (cm^3) \)
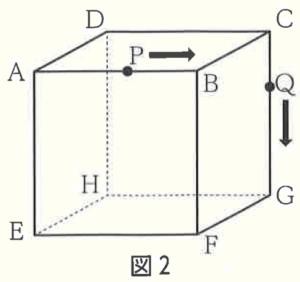
問2 右の図2は,図1の立方体において,2点 \( P,Q \) がそれぞれ頂点 \( A,C \) を同時に出発し,立方体の辺上を動きながら,頂点を移動する様子を示した図である。
点 \( P \) は毎秒 \( 5 \; cm \) の速さで立方体の頂点を,
頂点 \( A \) →頂点 \( B \) →頂点 \( F \) →頂点 \( G \) →頂点 \( C \)
と移動し,点 \( Q \) は毎秒 \( 3 \; cm \) の速さで立方体の頂点を,
頂点 \( C \) →頂点 \( G \) →頂点 \( F \) →頂点 \( B \) →頂点 \( A \)
と移動する。
2点 \( P,Q \) が重なる点を \( R \) とし,この立方体を3点 \( B,E,R \) を通る平面で切り,頂点 \( F \) を含む立体を \( S \) とする。
このとき,次の各問いに答えなさい。
(1) 2点 \( P,Q \) が重なるのは出発して何秒後か求めなさい。
【解説】
2点 \( P,Q \) は,5点 \( A,B,F,G,C \) を点 \( P \) は頂点 \( A \) から,点 \( Q \) は頂点 \( C \) から進むので,
辺 \( AB,BF,FG,GC \) をまとめて1本の線分として考えると,
線分 \( AC \) の長さは,\( 8 \times 4=32 \; (cm) \) になります。
出発してから \( x \) 秒後に2点 \( P,Q \) が重なるとすると,
出発してから重なるまでに点 \( P \) が進む距離は,\( 5x \; cm \),
出発してから重なるまでに点 \( Q \) が進む距離は,\( 3x \; cm \)
と表すことができ,2点 \( P,Q \) が進んだ距離の合計が \( 32 \; cm \) になるので,
\( 5x+3x=32 \)
\( x=4 \)(秒後)

(2) 立体 \( S \) の体積を求めなさい。
【解答】
\( \dfrac{128}{3} \; cm^3 \)
【解説】
点 \( Q \) が \( 4 \) 秒間に進む距離は \( 3 \times 4=12 \; (cm) \) なので,
\( CG=8 \; cm \) であることから,\( GR=4 \; cm \) になります。
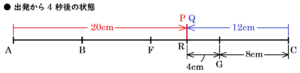
このとき,立体 \( S \) は右の図のような
三角すいになるので,体積は,
\( \left( 8 \times 4 \times \dfrac{1}{2} \right) \times 8 \times \dfrac{1}{3}=\dfrac{128}{3} \; (cm^3) \)
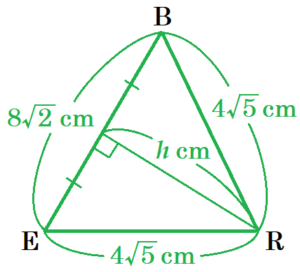
(3) 立体 \( S \) において,\( △BER \) を底面としたときの高さを求めなさい。
【解答】
\( \dfrac{4\sqrt{6}}{3} \; cm \)
【解説】
同じ立体の見る向きを変えても体積は変わらないので,
\( △BER \) の面積を \( M \),\( △BER \) を底面としたときの高さを \( H \) とすると,
\( M \times H \times \dfrac{1}{3}=\dfrac{128}{3} \)
となるので,\( △BER \) の面積がわかれば,高さを求めることができます。
\( △BER \) の3辺の長さは,三平方の定理より,
\( ER^2=8^2+4^2=80 \)
\( ER=4\sqrt{5} \; (cm) \)( \( ER>0 \) より)
\( BE^2=8^2+8^2=128 \)
\( BE=8\sqrt{2} \; (cm) \)( \( BE>0 \) より)
\( BR^2=8^2+4^2=80 \)
\( BR=4\sqrt{5} \; (cm) \)( \( BR>0 \) より)
で,\( BR=ER \) の二等辺三角形になっています。
\( △BER \) において,\( BE \) を底辺としたときの
高さを \( h \; cm \) とすると,
\( h^2=(4\sqrt{5})^2-(4\sqrt{2})^2=48 \)
\( h=4\sqrt{3} \; (cm) \)( \( h>0 \) より)
なので,\( △BER \) の面積は,
\( 8\sqrt{2} \times 4\sqrt{3} \times \dfrac{1}{2}=16\sqrt{6} \; (cm^2) \)
よって,立体 \( S \) の体積を方程式で表し,解くと,
\( 16\sqrt{6} \times H \times \dfrac{1}{3}=\dfrac{128}{3} \)
\( 16\sqrt{6}H=128 \)
\( H=\dfrac{8}{\sqrt{6}}=\dfrac{4\sqrt{6}}{3} \; (cm) \)
大問10
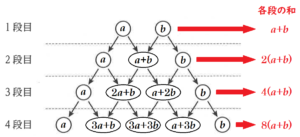
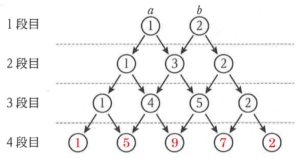
下の図1のように並べられた○の中に,次の規則にしたがって数を記入する。
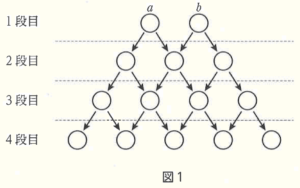
規則1 1段目には2つの自然数 \( a,b \) を記入する。
規則2 2段目以降は,左端に \( a \),右端に \( b \) を記入し,それ以外は左上の数と右上の数の和を
記入する。
下の図2は,\( a=1,b=2 \) として,規則にしたがって数を3段目まで記入したときの様子である。
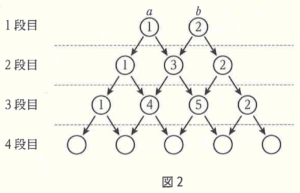
このとき,次の各問いに答えなさい。
問1 \( a=1,b=2 \) のとき,4段目に記入される5個の数を左から順に答えなさい。
真美さんは \( a,b \) を様々な値に変えて1段目から4段目まで数を記入し,その結果を考察して,次のように予想した。
1段目の数 \( a,b \) をどのように変えても,次のことが成り立つ。
予想1 2段目の3個の数の和は,1段目の2個の数の和の2倍となる。
予想2 3段目の4個の数の和は,1段目の2個の数の和の4倍となる。
予想3 4段目の5個の数の和は,1段目の2個の数の和の8倍となる。
真美さんは,まず予想1が成り立つことを次のように説明した。
予想1の説明
1段目の2個の数を \( a,b \) とすると,その和は \( a+b \)
2段目の3個の数を a と b を用いて左から順に表すと \( a,a+b,b \)
その和は \( a+(a+b)+b=2a+2b=2(a+b) \)
よって,2段目の3個の数の和は,1段目の2個の数の和の2倍となる。
次に,予想2が成り立つことを次のように説明した。
予想2の説明
1段目の2個の数を \( a,b \) とすると,その和は \( a+b \)
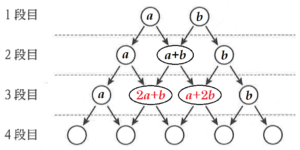
3段目の4個の数を \( a \) と \( b \) を用いて左から順に表すと \( a \), ア , イ ,\( b \)
その和は \( a+( \) ア \( )+( \) イ \( )+b=4a+4b=4(a+b) \)
よって,3段目の4個の数の和は,1段目の2個の数の和の4倍となる。
問2 上の ア , イ にそれぞれあてはまる最も適する式を答え,真美さんの予想2の説明を完成しなさい。ただし,式は同じ文字の項をまとめ,最も簡単な形で表すこと。
【解答】
ア ・・・ \( 2a+b \)
イ ・・・ \( a+2b \)
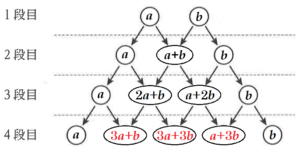
問3 予想3が成り立つことを,1段目の2個の数を \( a,b \) とし,4段目の5個の数を \( a \) と \( b \) を用いて表すことによって説明しなさい。
【解答】
1段目の2個の数を \( a,b \) とすると,その和は \( a+b \)
3段目の4個の数を \( a \) と \( b \) を用いて左から順に表すと \( a,2a+b,a+2b,b \)
4段目の5個の数を \( a \) と \( b \) を用いて左から順に表すと \( a,3a+b,3a+3b,a+3b,b \)
その和は
\( a+(3a+b)+(3a+3b)+(a+3b)+b=8a+8b \)
\( =8(a+b) \)
よって,4段目の5個の数の和は,1段目の2個の数の和の8倍となる。
問4 \( a=18,b=32 \) のとき,1段目から4段目までの○の中に記入された14個の数の和を求めなさい。
【解説】
予想1~予想3がすべて成り立つことから,1段目の2個の数を \( a,b \) とするとき,
各段に並ぶ数の和は,
1段目 ・・・ \( a+b \)
2段目 ・・・ \( 2(a+b) \)
3段目 ・・・ \( 4(a+b) \)
4段目 ・・・ \( 8(a+b) \)
と表すことができます。
ここから,14個の数の和は,
\( (a+b)+2(a+b)+4(a+b)+8(a+b)=15(a+b) \)
と表すことができます。
よって,\( a=18,b=32 \) のとき,14個の数の和は,
\( 15 \times (18+32)=750 \)