大問1
〔問1〕 次の (1)~(5) を計算しなさい。
(1) \( 2-6 \)
(2) \( \dfrac{8}{5}+\dfrac{7}{15} \times (-3) \)
【解説】
\( =\dfrac{8}{5}-\dfrac{7}{5} \)
\( =\dfrac{1}{5} \)
(3) \( 3(2a+b)-(a+5b) \)
【解説】
\( =6a+3b-a-5b \)
\( =5a-2b \)
(4) \( \dfrac{9}{\sqrt{3}}-\sqrt{75} \)
【解説】
\( =\dfrac{9 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}-5\sqrt{3} \)
\( =3\sqrt{3}-5\sqrt{3} \)
\( =-2\sqrt{3} \)
(5) \( a(a+2)+(a+1)(a-3) \)
【解説】
\( =a^2+2a+a^2-2a-3 \)
\( =2a^2-3 \)
〔問2〕 次の式を因数分解しなさい。
\( x^2-12x+36 \)
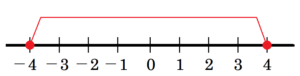
〔問3〕 絶対値が \( 4 \) 以下の整数はいくつあるか,求めなさい。
【解説】
絶対値が \( 4 \) の整数は \( -4 \) と \( 4 \) なので,
あてはまるのは,\( -4 \) 以上,\( 4 \) 以下の整数になります。
よって,\( -4,-3,-2,-1,0,1,2,3,4 \) の9個になります。
〔問4〕 次の表は,ある学年の生徒の通学時間を調査し,その結果を度数分布表にまとめたものである。
表中のア,イにあてはまる数をそれぞれ求めなさい。
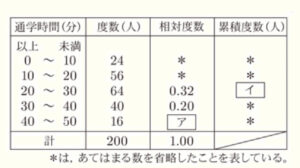
【解答】
ア ・・・ \( 0.08 \)
イ ・・・ \( 144 \)
【解説】
相対度数は,度数 \( \div \) データの総数 で求められるので,
\( 16 \div 200=0.08 \)
相対度数は,その階級より小さい階級の度数の和で求められるので,
\( 24+56+64=144 \)
〔問5〕 \( y \) は \( x \) の2乗に比例し,\( x=3 \) のとき,\( y=-18 \) である。
このとき,\( y \) を \( x \) の式で表しなさい。
【解説】
\( y \) が \( x \) の2乗に比例するとき,\( y=ax^2 \)( \( a \) は定数)で表されます。
\( x=3 \) のとき,\( y=-18 \) なので,代入すると,
\( -18=a \times 3^2 \)
\( 9a=-18 \)
\( a=-2 \)
よって,求める式は,\( y=-2x^2 \)
〔問6〕 右の図のように,円 \( O \) の周上に4点 \( A,B,C,D \) がある。
\( ∠BDC=39°,BC=3AB \) のとき,\( ∠x \) の大きさを求めなさい。
【解説】
\( ∠BDC \) は弧 \( BC \) に対する円周角,
\( ∠BOC \) は弧 \( BC \) に対する中心角なので,
\( ∠BOC=2∠BDC=78° \)
中心角の大きさは弧の長さに比例するので,
\(∠AOB:∠BOC=AB:BC\)
\(∠AOB:78°=1:3\)
\(∠AOB=26°\)
よって,\( ∠x=∠AOB+∠BOC=104° \)
大問2
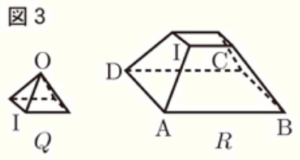
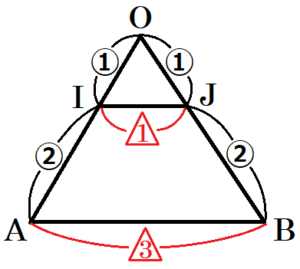
〔問1〕 図1の展開図をもとにして,図2のように正四角錐 \( P \) をつくった。
次の(1) ,(2)に答えなさい。
(1) 図2において,点 \( A \) と重なる点を図1の \( E,F,G,H \) の中から1つ選び,その記号をかきなさい。
【解答】
\( E \)

(2) 正四角錐 \( P \) の辺 \( OA \) 上に \( OI:IA=1:2 \) となる点 \( I \) をとる。
図3のように,点 \( I \) を通り,底面 \( ABCD \) に平行な平面で分けられた2つの立体をそれぞれ \( Q,R \) とする。
このとき,\( Q \) と \( R \) の体積の比を求め,最も簡単な整数の比で表しなさい。
【解説】
立体 \( Q \) と \( R \) を組み立てた状態で正面から見ると右の図のようになります。
切り口の線分と線分 \( OB \) との交点を点 \( J \) とすると,
\( OJ:JB=1:2 \) となるので,
\( △OIJ \) ∽ \( △OAB \) であり,相似比は \( 1:3 \) になります。
よって,\( AB=3IJ \) と表すことができます。
点 \( O \) から線分 \( AB \) に垂線をひき,切り口の線分との交点を点 \( K \),線分 \( AB \) との交点を点 \( L \) とすると,
\( △OIK \) ∽ \( △OAL \) であり,相似比は \( 1:3 \) になります。
よって,\( OL=3OK \) と表すことができます。
立体 \( Q \) の体積は,\( IJ^2 \times OK \times \dfrac{1}{3} \)
立体 \( P \) の体積は,\( AB^2 \times OL \times \dfrac{1}{3}=(3IJ)^2 \times 3OK \times \dfrac{1}{3} \)
\( =27 \times \left( IJ^2 \times OK \times \dfrac{1}{3} \right) \)
と表すことができるので,立体 \( Q \) と立体 \( P \) の体積の比は,\( 1:27 \) であるとわかります。
立体 \( R \) は,立体 \( P \) から立体 \( Q \) を除いたものなので,
立体 \( Q: \) 立体 \( R= \) 立体 \( Q:( \) 立体 \( P \; – \) 立体 \( Q) \)
\( =1:(27-1) \)
\( =1:26 \)
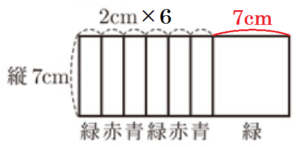
〔問2〕 1辺の長さが \( 7 \; cm \) の正方形である緑,赤,青の3種類の色紙がある。
この色紙を,図のように左から緑,赤,青の順に繰り返して右に \( 2 \; cm \) ずつずらして並べていく。
表は,この規則に従って並べたときの色紙の枚数,一番右の色紙の色,横の長さについてまとめたものである。
このとき,下の (1),(2) に答えなさい。

(1) 表中の □ にあてはまる色をかきなさい。
【解説】
緑・赤・青 が順番に繰り返されるので,3枚目,6枚目,・・・ と,3の倍数のときに青になります。
13枚目は12枚目(青)の次なので,緑になります。
(2) 色紙を \( n \) 枚並べたときの横の長さを \( n \) の式で表しなさい。
【解説】
例として,図の7枚並べた場合を考えると,
一番右の1枚だけ \( 7 \; cm \) すべてが見えています。
残りの6枚は,左端の \( 2 \; cm \) だけが見えるので,
合計の長さは,\( 2 \times 6+7 \; (cm) \) となります。
\( n \) 枚並べたときは,一番右の1枚だけ \( 7 \; cm \) すべてが見えて,
残りの \( n-1 \) 枚は,左端の \( 2 \; cm \) だけが見えているので,
合計の長さは,\( 2 \times (n-1)+7=2n+5 \; (cm) \) となります。
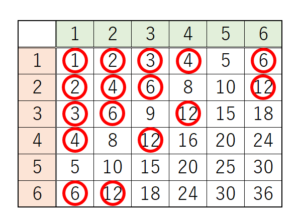
〔問3〕 2つのさいころを同時に投げるとき,出る目の数の積が12の約数になる確率を求めなさい。
ただし,さいころの1から6までのどの目が出ることも同様に確からしいものとする。
【解説】
2つのさいころ出る目の数の組み合わせとその積を表に表し,12の約数になるところに
○ をつけてみます。
12の約数になるのは16通り,すべての組み合わせは36通りなので,
確率は,\( \dfrac{16}{36}=\dfrac{4}{9} \)
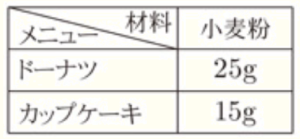
〔問4〕 右の表は,ある洋菓子店でドーナツとカップケーキをそれぞれ1個つくるときの小麦粉の分量を表したものである。
この分量にしたがって,小麦粉 \( 400 \; g \) を余らせることなく使用して,ドーナツとカップケーキをあわせて \( 18 \) 個つくった。
このとき,つくったドーナツとカップケーキはそれぞれ何個か,求めなさい。
ただし,答えを求める過程がわかるようにかきなさい。
【解答】
つくったドーナツの個数を \( x \) 個,カップケーキの個数を \( y \) 個とし,
つくった数の関係を方程式にすると,\( x+y=18 \) ・・・ ➀
使用した小麦粉の量の関係を方程式にすると,\( 25x+15y=400 \) ・・・ ➁
➀➁を連立方程式として解くと,
\( \left\{ \begin{array}{}
x+y=18 \;\; ・・・ \;\; ➀ \\
25x+15y=400 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁より,
\( 5x+3y=80 \) ・・・ ➁’
➁’\( – \) ➀\( \times 3\)
\( 2x=26 \)
\( x=13 \)
➀ に代入すると,
\( 13+y=18 \)
\( y=5 \)
よって,つくったドーナツの個数は \( 13 \) 個,カップケーキの個数は \( 5 \) 個
〔問5〕 次の箱ひげ図は,太郎さんを含む15人のハンドボール投げの記録を表したものである。
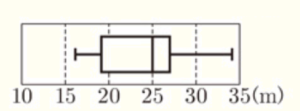
また,次の文は太郎さんと先生の会話の一部である。
太郎:先生,15人のハンドボール投げの記録の平均値は何 \( m \) ですか。わたしの記録は \( 24.0 \; m \) でした。
先生:平均値は \( 23.9 \; m \) です。
太郎:そうすると,わたしの記録は平均値より大きいから,15人の記録の中で上位8番以内に入りますね。
下線部の太郎さんの言った内容は正しくありません。その理由をかきなさい。
【解答】
箱ひげ図から中央値は \( 25.0 \; m \) であり,全員で15人なので,記録の良い方から8番目の人の記録だから。
大問3
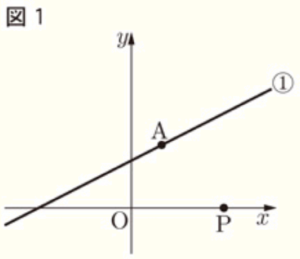
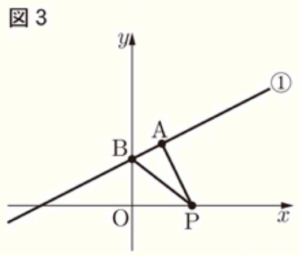
図1のように, 関数 \(y=\dfrac{1}{2}x+3 \) ・・・ ➀ のグラフ上に点 \( A(2, 4) \) があり,\( x \) 軸上に点 \( P \) がある。
次の〔問1〕~〔問4〕に答えなさい。
〔問1〕 関数 \(y=\dfrac{1}{2}x+3 \) について,\( x \) の増加量が \( 4 \) のとき,
\( y \) の増加量を求めなさい。
【解説】
傾き \( =\dfrac{y \; の増加量}{x \; の増加量} \) で求めることができるので,
\( y \)の増加量 \( = \) 傾き \( \times \; x \) の増加量
\( =\dfrac{1}{2} \times 4 \)
\( =2 \)
〔問2〕 \( P \) の \( x \) 座標が \( 6 \) のとき,直線 \( AP \) の式を求めなさい。
【解説】
直線 \( AP \) は,\( A(2, 4),P(6, 0) \) を通るので,
傾き \( =\dfrac{0-4}{6-2}=-1 \)
この直線の式を \( y=-x+b \) とすると,\( P(6, 0) \) を通るので,
\( 0=-6+b \)
\( b=6 \)
よって,直線 \( AP \) の式は,\( y=-x+6 \)
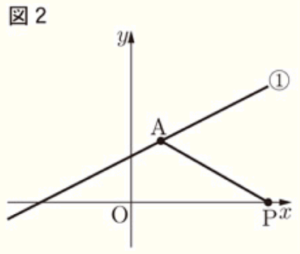
〔問3〕 図2のように,\( ∠APO=30° \) のとき,\( P \) の \( x \) 座標を
求めなさい。
【解説】
点 \( A \) から \( x \) 軸に垂線をひき,交点を点 \( C \) とすると,
\( △ACP \) は,\( 30°,60°,90° \) の直角三角形なので,
\( AC:CP=1:\sqrt{3} \)
\( A(2, 4) \) より,\( AC=4 \) なので,
\( AC:CP=1:\sqrt{3} \)
\( 4:CP=1:\sqrt{3} \)
\( CP=4\sqrt{3} \)
\( A(2, 4) \) より,\( OC=2 \) なので,
\( P \) の \( x \) 座標は,\( 2+4\sqrt{3} \)
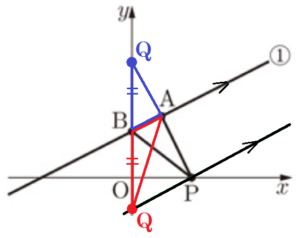
〔問4〕 図3のように,➀ のグラフと \( y \) 軸との交点を \( B \) とする。
また,\( y \) 軸上に点 \( Q \) をとり,\( △ABP \) と \( △ABQ \) の面積が等しくなるようにする。
\( P \) の \( x \) 座標が \( 4 \) のとき,\( Q \) の座標をすべて求めなさい。
【解説】
\( △ABP \) と \( △ABQ \) は辺 \( AB \) が共通なので,等積変形の考え方から,
点 \( P \) を通り,➀ と平行な直線と \( y \) 軸との交点が求める点 \( Q \) になります。
また,この場合の点 \( Q \) は ➀ の下側にありますが上側にもできることに注意が必要です。
点 \( P \) を通り,➀ と平行な直線について考えると,
平行な直線の傾きは等しいので,傾きは \( \dfrac{1}{2} \) です。
この直線の式を \(y=\dfrac{1}{2}x+b \) とすると,\( P(4, 0) \) を通るので,
\( 0=\dfrac{1}{2} \times 4+b \)
\( b=-2 \)
となり,この直線の式は,\(y=\dfrac{1}{2}x-2 \)
点 \( Q \) はこの直線と,\( y \) 軸との交点なので,\( Q(0,-2) \)
点 \( Q \) は,➀ の上側にもとることができます。
上側に作った青の\( △ABQ \) も,赤の\( △ABQ \) と高さが共通なので,
面積が等しいとき,底辺の長さも等しくなります。
\( B(0,3),Q(0,-2) \) より,\( BQ=5 \) なので,
上側の点 \( Q \) の座標は,\( Q(0,8) \) になります。
大問4
平行四辺形 \( ABCD \) の辺 \( BC \) 上に点 \( E \) がある。
ただし,辺 \( BC \) の長さは辺 \( AB \) の長さより長いものとする。
次の〔問1〕~〔問4〕に答えなさい。
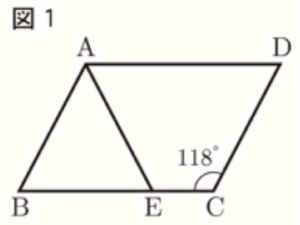
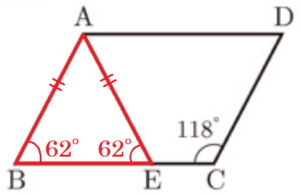
〔問1〕 図1のように,\( AB=AE,∠BCD=118° \) のとき,\( ∠BAE \) の大きさを求めなさい。
【解説】
平行四辺形のとなりあう角の和は \( 180° \) になるので,
\( ∠ABE=180°-118°=62° \)
\( △ABE \) は二等辺三角形なので,
\( ∠BAE=180°-2∠ABE=56° \)
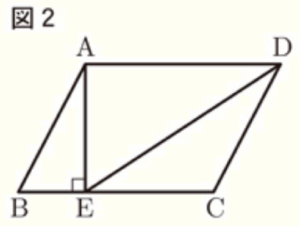
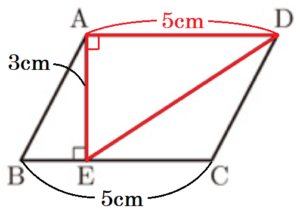
〔問2〕 図2のように,\( BC=5 \; cm,AE=3 \; cm \),
\( ∠AEB=90° \) のとき,線分 \( DE \) の長さを求めなさい。
【解答】
\( \sqrt{34} \; cm \)
【解説】
平行四辺形の向かい合う辺は平行で長さが等しいので,
\( AD//BC \) より,錯角は等しく,
\( ∠EAD=∠AEB=90° \)
また,\( AD=BC=5 \; cm \)
よって,\( △ADE \) において,三平方の定理より,
\( DE^2=AD^2+AE^2 \)
\( =5^2+3^2 \)
\( =34 \)
\( DE=\sqrt{34} \; (cm) \) (\( DE>0 \) より)
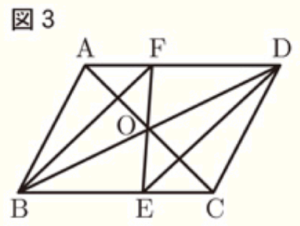
〔問3〕 図3のように,平行四辺形 \( ABCD \) の対角線の交点を \( O \) とし,直線 \( EO \) と \( AD \) の交点を \( F \) とする。
このとき,四角形 \( BEDF \) は平行四辺形であることを証明しなさい。
【解答】
\( △BOE \) と \( △DOF \) において,
平行四辺形の対角線はそれぞれの中点で交わるので,
\( BO=DO \) ・・・ ➀
平行四辺形の向かい合う辺は平行なので,錯角は等しく,
\( ∠OBE=∠ODF \) ・・・ ➁
対頂角は等しいので,
\( ∠BOE=∠DOF \) ・・・ ➂
➀➁➂より,1組の辺とその両端の角がそれぞれ等しいので,
\( △BOE≡△DOF \)
対応する辺の長さは等しいので,
\( OE=OF \) ・・・ ➃
➀➃より,対角線がそれぞれの中点で交わっているので,
四角形 \( BEDF \) は平行四辺形である。
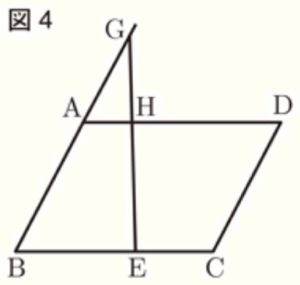
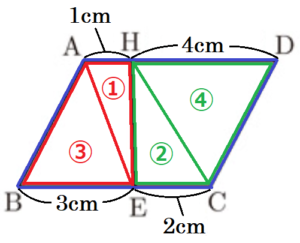
〔問4〕 図4のように,\( AB=4 \; cm,BE=3 \; cm,EC=2 \; cm \) のとき,辺 \( BA \) の延長上に \( AG=2 \; cm \) となるように点 \( G \) をとる。
また,\( GE \) とADの交点を \( H \) とする。
このとき,台形 \( ABEH \) の面積は,平行四辺形 \( ABCD \) の面積の何倍になるか,求めなさい。
【解答】
\( \dfrac{2}{5} \) 倍
【解説】
\( △GAH \) と \( △GBE \) において,
\( ∠GAH=∠GBE,∠G \) は共通
なので,2組の角が等しく,\( △GAH \) ∽ \( △GBE \)
対応する辺の比は等しいので,
\( GA:GB=AH:BE \)
\( 2:(2+4)=AH:3 \)
\( 6AH=6 \)
\( AH=1 \; (cm) \)
平行四辺形の向かい合う辺は長さが等しいので,
\( BE=3 \; cm,EC=2 \; cm,AH=1 \; cm \) より,\( HD=4 \; cm \)
補助線 \( AE,CH \) をひくと,
\( △ABE,△AEH,△CEH,△CDH \) は,
高さが等しいので,底辺の長さの比が面積比となります。
よって,\( △AEH \) の面積を \( 1 \) とすると,
\( △ABE=3,△CEH=2,△CDH=4 \) となります。
以上より,
台形 \( ABEH=△ABE+△AEH=3+1=4 \),
平行四辺形 \( ABCD=△ABE+△AEH+△CEH+△CDH=3+1+2+4=10 \)
なので,
台形 \( ABEH \) の面積は,平行四辺形 \( ABCD \) の面積の \( \dfrac{4}{10}=\dfrac{2}{5} \) 倍