大問１
１ \( -9+7 \)
２ \( \dfrac{5}{8}+(-1) \div 4 \)
３ \( 4^2-(-3)^2 \)
４ \( \dfrac{6}{\sqrt{2}}+\sqrt{8} \)
５ \( -\dfrac{1}{5}a^2 \times 45b^3 \div (−ab) \)
大問２
１ 家から毎分 \( 60 \; m \) で \( x \) 分間歩き，途中から毎分 \( 80 \; m \) で歩いたところ，家を出発してからちょうど \( 10 \) 分後，駅に着いた。このとき，\( 60x+80(10-x) \) が表している数量を，次のア～エから１つ選び，その記号を書きなさい。
ア 家から駅まで歩いた時間
イ 家から駅まで歩いた平均の速さ
ウ 毎分 \( 60 \; m \) で歩いた道のり
エ 家から駅までの道のり
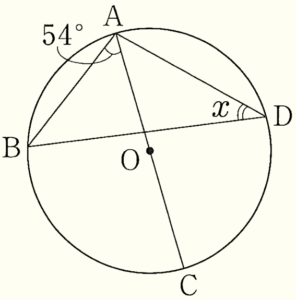
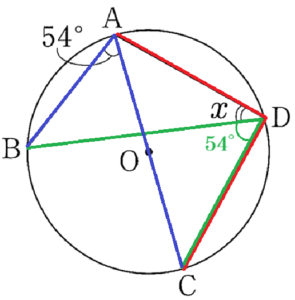
２ 右の図において，点 \( O \) は円の中心であり，点 \( A，B，C，D \) は円周上の点である。また，線分 \( AC \) は直径であり，\( ∠BAC=54° \) である。
このとき，\( ∠x \) の大きさを求めなさい。
\( ∠ADC \) は直径に対する円周角なので，
\( ∠ADC=∠x+∠BDC=90° \) ･･･ ➀
\( ∠BAC，∠BDC \) は \( \stackrel{\huge\frown}{ BC } \) に対する円周角なので，
\( ∠BDC=∠BAC=54° \)
➀に代入すると，
\( ∠x+54°=90° \)
\( ∠x=36° \)
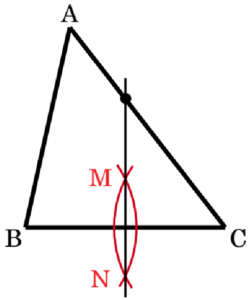
３ 右の図において，\( △ABC \) の辺 \( AC \) 上にあって，頂点 \( B \) からの距離と頂点 \( C \) からの距離が等しい点を作図によって求めなさい。このとき，求めた点を●で示しなさい。
ただし，作図には定規とコンパスを用い，作図に用いた線は消さずに残しておくこと。
手順１ ･･･ ２点 \( B，C \) を中心に円弧を描く
（交点を \( M，N \) とします）
手順２ ･･･ ２点 \( M，N \) を通る直線を描く
手順２の直線と辺 \( AC \) の交点が求める点になります。
４ \( y \) は \( x \) に反比例し，\( x \) の値が \( 3 \) のとき \( y \) の値は \( -12 \) である。\( x \) の値が \( 4 \) のときの \( y \) の値を求めなさい。
５ 箱の中に５本のくじがあり，そのうち３本が当たりくじである。箱の中から，Ａさんが１本ひく。ひいたくじを箱の中に戻さないで，続けてＢさんが１本ひく。このとき，２人とも当たりくじをひく確率を求めなさい。
ただし，どのくじをひくことも同様に確からしいものとする。
Ａさん，Ｂさんがひくくじの組み合わせを樹形図に書き出すと，
すべての組み合わせは２０通り，２人とも当たりくじをひく組み合わせは６通りなので，
求める確率は \( \dfrac{6}{20}=\dfrac{3}{10} \)
大問３
１ ある中学校では６月１日からの２週間，衣替えの移行期間となる。Ｃさんは５月から暑さを感じたため，この移行期間が妥当であるか疑問をもった。そこで，昔と比べて５月の気温が高くなっているのではないかと予想し，中学校がある地域の５月の平均気温を調べて，その傾向をみることにした。
図１は，１９６５年から２０２４年までの６０年分の，それぞれの年の５月の平均気温を調べ，そのデータを１５年ごとのまとまりとして４つに分けて箱ひげ図で表したものである。
このとき，次の（１），（２）に答えなさい。
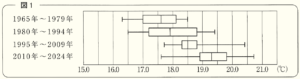
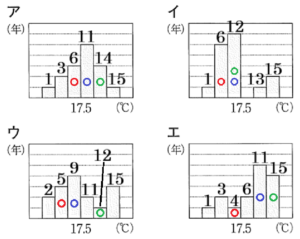
（１） １９６５年～１９７９年の箱ひげ図と同じデータを使ってかいたヒストグラムを，次のア～エから１つ選び，その記号を書きなさい。
第１四分位数は気温の低い方から４番目の値で，\( 17.0 \; C^\circ \) 以上 \( 17.5 \; C^\circ \) 未満の階級に含まれています。
中央値は気温の低い方から８番目の値で，\( 17.5 \; C^\circ \) 以上 \( 18.0 \; C^\circ \) 未満の階級に含まれています。
第３四分位数は気温の低い方から１２番目の値で，\( 18.0 \; C^\circ \) 以上 \( 18.5 \; C^\circ \) 未満の階級に含まれています。
次に，それぞれのヒストグラムに累積度数を書き込み，
第１四分位数（４番目の値）が含まれている階級に ○，
中央値（８番目の値）が含まれている階級に ○，
第３四分位数（１２番目の値）が含まれている階級に ○
をつけると，箱ひげ図とすべてが合致しているのは ア のヒストグラムになります。
（２） 「この地域の２０１０年～２０２４年の５月の平均気温は，１９９５年～２００９年の５月の平均気温より高くなっている傾向にある」と主張できる。その理由を，１９９５年～２００９年と２０１０年～２０２４年の２つの箱ひげ図の箱に着目して説明しなさい。
箱ひげ図の箱の部分には約５０％の数のデータが含まれています。
２つの箱ひげ図の最大値と最小値がほぼ同じで，箱の位置が右側にあるということは
１９９５年～２００９年では，約半分の年で平均気温が\( 18.3 \; C^\circ \) 以上 \( 18.8 \; C^\circ \) 未満であるのに対して，
２０１０年～２０２４年では，約半分の年で平均気温が\( 18.9 \; C^\circ \) 以上 \( 20.8 \; C^\circ \) 未満になっています。
ここから，「２０１０年～２０２４年の５月の平均気温は，１９９５年～２００９年の５月の平均気温より高くなっている傾向にある」といえます。
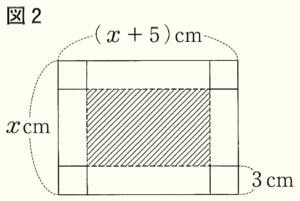
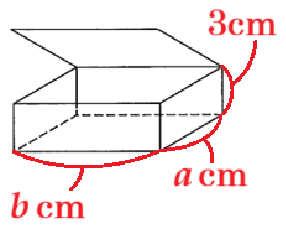
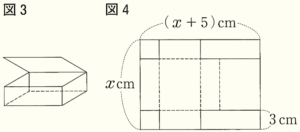
２ 横が縦より \( 5 \; cm \) 長い長方形の紙がある。この紙の縦の長さを \( x \; cm \) とする。
このとき，次の（１），（２）に答えなさい。ただし，紙の厚さは考えないものとする。
（１） ふたのない直方体の容器を作る。そのため，図２のように，この紙の４すみから１辺が \( 3 \; cm \) の正方形を切り取った。この容器の底面積（斜線部分）は,次の式で表すことができる。
\( (x-6)(x-1) \)
このとき，底面積が \( 36 \; cm^2 \) となるような \( x \) の値を求めなさい。
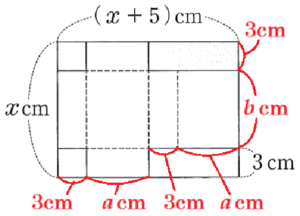
（２） 図３のような，ふたのある直方体の箱を作る。そのため，図４のように，図２の４すみの正方形のうち２つを長方形に変えて切り取った。
このとき，直方体の容積を表す式を求めなさい。
直方体の底面の縦の長さを \( a \; cm \)，
横の長さを \( b \; cm \) とすると，
高さ（深さ）は \( 3 \; cm \) なので，
この直方体の容積は
\( a \times b \times 3=3ab \) ･･･ ➀
と表すことができます
図４の展開図に各辺の長さを書き込むと
右の図のようになるので，
紙の縦の長さの関係を方程式で表すと，
\( x=3+b+3 \)
\( b=x-6 \)
紙の縦の長さの関係を方程式で表すと，
\( x+5=2(3+a) \)
\( x+5=2a+6 \)
\( 2a=x-1 \)
\( a=\dfrac{x-1}{2} \)
これらを➀に代入すると，
\( 3 \times \dfrac{x-1}{2} \times (x-6)=\dfrac{3}{2}(x-1)(x-6) \)
大問４
電気を使って温度を保ったまま，お湯をためておくことができる電気給湯器がある。この電気給湯器は360Lで満水状態となる。また，表のように常に一定のお湯を出したり，ためたりすることができるスイッチがついている。なお,複数のスイッチを同時に押すことはできない。
最初にスイッチを押してから \( x \) 分後の電気給湯器の中のお湯の量を \( y \; L \) として，\( x \) と \( y \) の関係を考えることとする。
このとき，次の１～３に答えなさい。
１ 満水状態からスイッチＡを押し，電気給湯器の中のお湯が
なくなるまでの \( x \) と \( y \) の関係を表した式は，右のように
表すことができる。
このとき，次の（１），（２）に答えなさい。
\( y=-12x+360 \)
\( x \) の変域は，\( 0≦x≦ 30 \)
（１） 式の定数の部分 \( 360 \) が表しているものを，次のア～エから１つ選び，その記号を書きなさい。
ア 電気給湯器の中のお湯がなくなるまでにかかる時間
イ 満水状態の電気給湯器の中のお湯の量
ウ \( 30 \) 分後の電気給湯器の中のお湯の量
エ \( 1 \) 分間あたりの電気給湯器の中のお湯の増加量
（２） \( x \) の増加量が \( 10 \) のとき，\( y \) の増加量を求めなさい。
２ 満水状態からスイッチＢを押し，お湯を出し続けるとき，\( 5 \) 分後の電気給湯器の中のお湯の量を求めなさい。
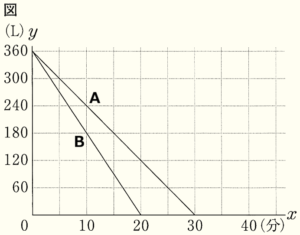
３ 図のＡはスイッチＡを押した場合について，ＢはスイッチＢを押した場合について，満水状態から電気給湯器の中のお湯がなくなるまでの \( x \) と \( y \) の関係を表したグラフである。
このとき，次の（１），（２）に答えなさい。
（１） 満水状態からスイッチＡを押した場合とスイッチＢを押した場合の電気給湯器の中のお湯が \( 180 \; L \) になるまでにかかる時間の違いを，図のグラフから求めることができる。その方法を説明しなさい。
ただし，実際に求める必要はない。
（２） 満水状態からスイッチＡを押し，しばらくお湯を出した後，\( 20 \) 分間だけスイッチＣに切り替え，電気給湯器の中にお湯をためた。その後，満水状態になる前にスイッチＢに切り替え，電気給湯器の中のお湯がなくなるまでお湯を出した。満水状態からお湯がなくなるまでに，\( 55 \) 分間かかった。このとき，スイッチＣに切り替えてから，スイッチＢに切り替えるまでの \( x \) と \( y \) の関係を表した式と，そのときの \( x \) の変域を求めなさい。
大問５
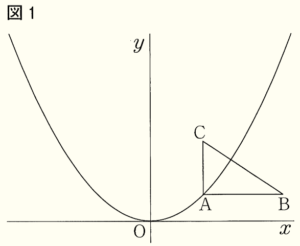
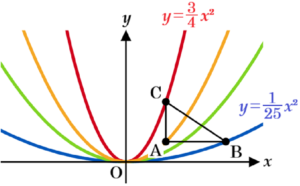
図１，２において，関数 \( y=ax^2(a>0) \) のグラフと点 \( A，B，C \) がある。点の座標は，それぞれ
\( A(2，1)，B(5，1)，C(2，3) \) である。点 \( A，B，C \) を頂点とする三角形は， \( ∠CAB \) が直角である直角三角形である。
このとき，次の１～３に答えなさい。
１ 図１において，グラフが点 \( A \) を通る。
このとき，次の（１），（２）に答えなさい。
（１） \( a \) の値を求めなさい。
（２） \( x \) の変域が \( -4≦x≦2 \) のとき，\( y \) の値の最小値を求めなさい。また，そのときの \( x \) の値も求めなさい。
２ グラフと直角三角形 \( ABC \) の周が２点で交わっているとき，\( a \) のとりうる値の範囲を求めなさい。
\( y=ax^2(a>0) \) のグラフは，\( a \) の値が小さくなるほどグラフの開き具合が大きくなります。
グラフと直角三角形 \( ABC \) の周が１点だけで交わるのは，
グラフが点 \( B \) を通るときと点 \( C \) を通るときなので，
点 \( C \) を通るときの \( a \) の値が最大で，
そこから \( a \) の値を小さくするほど
グラフは 赤 → オレンジ → 緑 → 青 と開き具合が大きくなっていき，
この間は２点で交わることになります。
そして，点 \( B \) を通るときの \( a \) の値が最小になり，１点だけでしか交わらなくなります。
グラフが点 \( C(2，3) \) を通るときの \( a \) の値は，
\( 3=a \times 2^2 \)
\( a=\dfrac{3}{4} \)
グラフが点 \( B(5，1) \) を通るときの \( a \) の値は，
\( 1=a \times 5^2 \)
\( a=\dfrac{1}{25} \)
なので，\( a \) のとりうる値の範囲は，
\( \dfrac{1}{25}<a<\dfrac{3}{4} \)
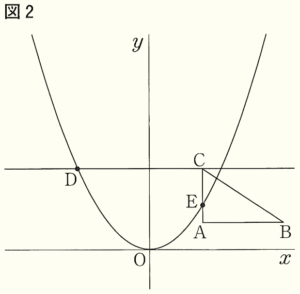
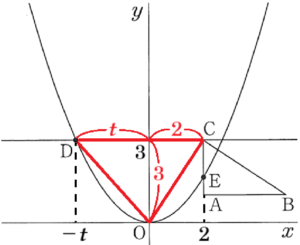
３ 点 \( C \) を通り \( x \) 軸に平行な直線とグラフとの交点のうち，\( x \) 座標が負である点を点 \( D \) とする。\( △OCD \) の面積が \( 7 \) となるとき，図２のようにグラフは辺 \( AC \) 上の点 \( E \) で交わった。
このとき，点 \( D \)，点 \( E \) の座標をそれぞれ求めなさい。
点 \( D \) の \( x \) 座標を \( -t \) とし，
\( △OCD \) の底辺を \( CD \) とすると，
\( CD \) の長さは \( t+2 \) と表すことができます。
また，点 \( D \) の \( y \) 座標が \( 3 \)
であることから，高さは \( 3 \) です。
\( △OCD \) の面積は \( 7 \) なので，
\( (t+2) \times 3 \times \dfrac{1}{2}=7 \)
\( t+2=\dfrac{14}{3} \)
\( t=\dfrac{8}{3} \)
であり，点 \( D \) の座標は \( D \left( -\dfrac{8}{3}，3 \right) \)
\( y=ax^2 \) のグラフは \( D \left( -\dfrac{8}{3}，3 \right) \) を通るので，
\( 3=a \times \left( -\dfrac{8}{3} \right)^2 \)
\( 3=\dfrac{64}{9}a \)
\( a=\dfrac{27}{64} \)
なので，２次関数を表す式は \( y=\dfrac{27}{64}x^2 \)
点 \( E \) は，\( y=\dfrac{27}{64}x^2 \) 上の点で，\( x \) 座標が \( 2 \) なので，
\( y \) 座標の値は，
\( y=\dfrac{27}{64} \times 2^2=\dfrac{27}{16} \)
よって，点 \( E \) の座標は \( E \left( 2，\dfrac{27}{16} \right) \)
大問６
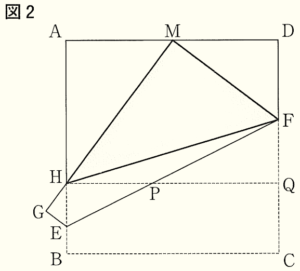
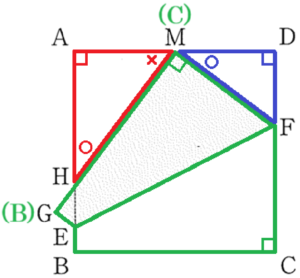
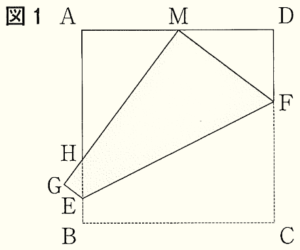
ある本の中で，正方形の折り紙の１辺を３等分する点の１つを見つける方法が，次のように書かれていた。
３等分する点の1つを見つける方法
図１のように，正方形 \( ABCD \) を頂点 \( C \) が辺 \( AD \) の中点 \( M \) に重なるように折り，折り目の線分を \( EF \) とする。このとき頂点 \( B \) が移動した点を \( G \)，線分 \( MG \) と辺 \( AB \) の交点を \( H \) とする。点 \( H \) は辺 \( AB \) を３等分する点の１つとなる。
\( \phantom{ } \)
このとき，次の１～３に答えなさい。ただし，紙の厚さは考えないものとする。
１ 図１において，\( △AHM \) ∽ \( △DMF \) となることを証明しなさい。
\( △AHM \) と \( △DMF \) において，
正方形の内角なので，
\( ∠HAM=∠MDF=90° \) ･･･ ➀
\( △AHM \) は \( ∠HAM=90° \) の直角三角形なので，
\( ∠AHM=180°-(∠HAM+∠AMH) \)
\( =90°-∠AMH \) ･･･ ➁
正方形の内角なので，
\( ∠BCF=90° \)
点 \( M \) は点 \( C \) を折り返した点なので，
\( ∠GMF=∠BCF=90° \) ･･･ ➂
３点 \( A，M，D \) は一直線上の点なので，➂より
\( ∠DMF=180°-(∠MDF+∠AMH) \)
\( =90°-∠AMH \) ･･･ ➃
➁➃より，
\( ∠AHM=∠DMF\) ･･･ ➄
➀➄より，２組の角がそれぞれ等しいので，
\( △AHM \) ∽ \( △DMF \)
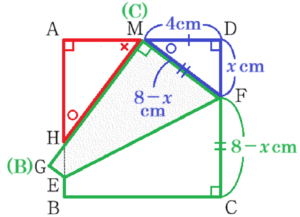
２ この本の中で，１辺の長さが \( 8 \; cm \) の正方形の折り紙を使って，点 \( H \) が辺 \( AB \) を３等分する点の１つとなることの説明が、次のように書かれていた。
（１） には \( x \) を用いた式を， （２） には当てはまる数をそれぞれ書きなさい。
線分 \( DF \) の長さを \( x \; cm \) としたとき，点 \( M \) は点 \( C \) が移動した点であることから，線分 \( MF \) の長さを \( x \) を用いて表すと， （１） \( cm \) となる。\( △DMF \) が直角三角形であることから，\( x \) の値は （２） である。また，\( △AHM \) ∽ \( △DMF \) であることから線分 \( AH \) の長さがわかり，点 \( H \) は辺 \( AB \) を３等分する点の１つとなる。
（１）
正方形 \( ABCD \) の１辺が \( 8 \; cm \) ということは，
\( DC=8 \; cm \) なので，
\( CF=DC-DF \)
\( =8-x \; (cm) \)
点 \( M \) は点 \( C \) を折り返した点なので，
\( MF=CF=8-x \; (cm) \)
（２） ･･･ \( 8-x \)
点 \( M \) は線分 \( AD \) の中点なので，
\( DM=\dfrac{1}{2}AD=4 \; (cm) \)
\( △DMF \) において，三平方の定理より，
\( DF^2+DM^2=MF^2 \)
\( x^2+4^2=(8-x)^2 \)
\( x^2+16=x^2-16x+64 \)
\( 16x=48 \)
\( x=3 \; (cm) \)
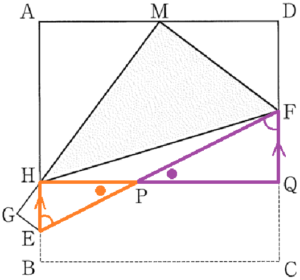
３ 図２において，図１の点 \( H \) を通り辺 \( BC \) に平行な直線と線分 \( EF \)，辺 \( DC \) との交点をそれぞれ \( P，Q \) とし，辺 \( AD \) の長さを \( 8 \; cm \) とする。
このとき，次の（１），（２）に答えなさい。
（１） 線分 \( HP \) と線分 \( PQ \) の長さの比を，最も簡単な整数の比で表しなさい。
正方形の向かい合う辺は平行であることから，
\( EH//FQ \) より，\( ∠PEH=∠PFQ \)
対頂角は等しいので，\( ∠EPH=∠FPQ \)
であり，２組の角がそれぞれ等しいので
\( △PEH \) ∽ \( △PFQ \) になっています。
ここから，対応する辺の比は等しいので，
\( HP：PQ=EH：FQ \) であり，
線分 \( EH \) と 線分 \( FQ \) の長さがわかれば
\( HP：PQ \) を求めることができます。
【線分 \( FQ \) の長さを求める】
問２より \( DF=3 \; cm \) なので，
\( CF=8-3=5 \; (cm) \)
点 \( M \) は点 \( C \) を折り返した点なので，
\( FM=CF=5 \; (cm) \)
点 \( M \) は線分 \( AD \) の中点なので，
\( DM=AM=\dfrac{1}{2}AD=4 \; (cm) \)
\( △AHM \) ∽ \( △DMF \) より，
\( AH：DM=AM：DF \)
\( AH：4=4：3 \; (cm) \)
\( AH=\dfrac{16}{3} \; (cm) \)
ここから，
\( HB=AB-AH \)
\( =8-\dfrac{16}{3} \)
\( =\dfrac{8}{3} \; (cm) \)
\( \phantom{ } \)
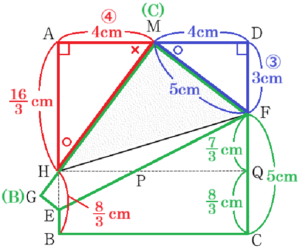
\( HQ//BC \) より，\( QC=HB=\dfrac{8}{3} \; cm \) なので，
\( FQ=CF-QC \)
\( =5-\dfrac{8}{3} \)
\( =\dfrac{7}{3} \; (cm) \)
【線分 \( EH \) の長さを求める】
点 \( M \) は点 \( C \) を折り返した点なので，
\( MF=CF=5 \; (cm) \)
\( △AHM \) ∽ \( △DMF \) で相似比は \( 4:3 \) なので，
\( HM：MF=AM：DF \)
\( HM：5=4：3 \; (cm) \)
\( HM=\dfrac{20}{3} \; (cm) \)
\( GM=BC=8 \; cm \) なので，
\( GH=GM-HM \)
\( =8-\dfrac{20}{3} \)
\( =\dfrac{4}{3} \; (cm) \)
点 \( G \) は点 \( B \) を折り返した点なので，
\( ∠EGH=∠EBC=∠MAH=90° \)
対頂角は等しいので，
\( ∠GHE=∠AHM \)
２組の角がそれぞれ等しいので
\( △GHE \) ∽ \( △AHM \)
対応する辺の比は等しいので，
\( HE：HM=GH：AH \)
\( HE：\dfrac{20}{3}=\dfrac{4}{3}：\dfrac{16}{3} \; (cm) \)
\( 3HE：20=4：16 \; (cm) \)
\( HE=\dfrac{5}{3} \; (cm) \)
\( \phantom{ } \)
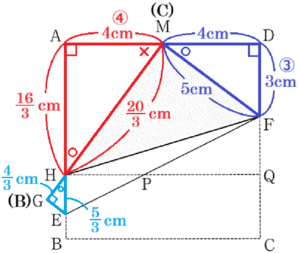
以上より，
\( HP：PQ=HE：FQ \)
\( =\dfrac{5}{3}：\dfrac{7}{3}\)
\( =5：7\)
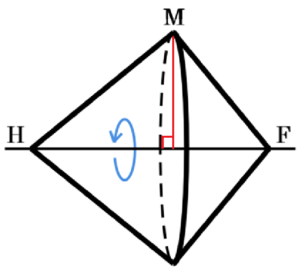
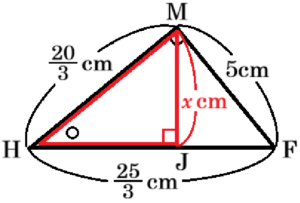
（２） \( △MHF \) を，直線 \( HF \) を軸として回転させてできる立体の体積を求めなさい。
ただし，円周率は \( \pi{} \) とする。
\( △MHF \) を，直線 \( HF \) を軸として
回転させてできる立体は右の図のような円すいを
２つくっつけた形になり，点 \( M \) から
線分 \( HF \) にひいた垂線が半径になります。
点 \( M \) から線分 \( HF \) に垂線をひいた交点を
\( J \) とすると，
\( △MHF \) は直角三角形であり，
\( HM：FM=\dfrac{20}{3}：5 \)
\( =20：15 \)
\( =4：3 \)
なので，３辺の比は \( 3：4：5 \) になっています。
ここから，\( HF \) の長さは，
\( HF=\dfrac{5}{3} \times 5=\dfrac{25}{3} \; (cm) \)
\( HJ=x \; cm \) とすると，
\( ∠H \) は共通，\( ∠HJM=∠HMF=90° \)
より，２組の角がそれぞれ等しいので
\( △JHM \) ∽ \( △MHF \) であり，
\( MJ：FM=HM：HF \)
\( x：5=\dfrac{20}{3}：\dfrac{25}{3} \)
\( x：5=4：5 \)
\( x=4 \; (cm) \)
\( HJ=y \; cm，FJ=z \; cm \) とすると，
\( HF=HJ+FJ=y+z=\dfrac{25}{3} \; cm \) なので，
求める立体の体積は，
\( (\pi{} \times 4^2) \times y \times \dfrac{1}{3}+(\pi{} \times 4^2) \times z \times \dfrac{1}{3} \)
\( =\dfrac{16\pi{}}{3}y+\dfrac{16\pi{}}{3}z \)
\( =\dfrac{16\pi{}}{3}(y+z) \)
\( =\dfrac{16\pi{}}{3} \times \dfrac{25}{3} \)
\( =\dfrac{400}{9}\pi{} \; (cm^3) \)
