大問1
(1) \( 13+3 \times (-2) \) を計算しなさい。
【解説】
\( =13-6 \)
\( =7 \)
(2) \( \dfrac{1}{3}a-\dfrac{5}{4}a \) を計算しなさい。
【解答】
\( -\dfrac{11}{12}a \)
【解説】
\( =\dfrac{4a-15a}{12} \)
\( =-\dfrac{11}{12}a \)
(3) 次の等式を〔 〕内の文字について解きなさい。
\( 3x+7y=21 \) 〔 \( x \) 〕
【解答】
\( x=\dfrac{-7y+21}{3} \)
【解説】
\( 3x=-7y+21 \)
\( x=\dfrac{-7y+21}{3} \)
(4) 次の連立方程式を解きなさい。
\( 2x+y=5x+3y=-1 \)
【解説】
\( \left\{ \begin{array}{}
2x+y=-1 \;\; ・・・ \;\; ➀ \\
5x+3y=-1 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀\( \times 3 \; – \)➁
\( x=-2 \)
➀に代入すると,
\( 2 \times (-2)+y=-1 \)
\( -4+y=-1 \)
\( y=3 \)
(5) \( \dfrac{9}{\sqrt{3}}-\sqrt{12} \) を計算しなさい。
【解説】
\( =\dfrac{9 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}-2\sqrt{3} \)
\( =\dfrac{9\sqrt{3}}{3}-2\sqrt{3} \)
\( =3\sqrt{3}-2\sqrt{3} \)
\( =\sqrt{3} \)
(6) 次の式を因数分解しなさい。
\( x^2-2x-24 \)
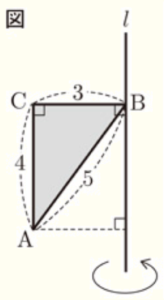
(7) 下の図の \( △ABC \) は,辺 \( AB,BC,CA \) の長さがそれぞれ \( 5,3,4 \) の直角三角形です。この三角形を直線 \( l \) を軸として1回転させてできる回転体の体積を求めなさい。ただし,辺 \( BC \) と \( l \) は垂直である。
【解説】
点 \( A \) から直線 \( l \) に垂線をひき,交点を点 \( D \) とします。
四角形 \( ADBC \) を直線 \( l \) を軸として1回転させると,半径 \( 3 \),高さ \( 4 \) の円柱
\( △ADB \) を直線 \( l \) を軸として1回転させると,半径 \( 3 \),高さ \( 4 \) の円すい
となり,求める回転体の体積はこの円柱から円すいをひいたものになります。
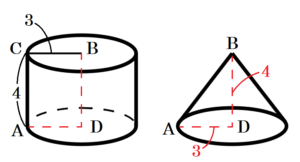
円柱の体積 \( =\pi{} \times 3^2 \times 4=36\pi{} \)
円すいの体積 \( =\pi{} \times 3^2 \times 4 \times \dfrac{1}{3}=12\pi{} \)
求める回転体の体積 \( =36\pi{}-12\pi{}=24\pi{} \)
(8) 下のデータは,ある生徒12人の先月読んだ本の冊数を調べ,冊数が少ない順に並べたものです。第3四分位数を求めなさい。

【解説】
第3四分位数は,少ない方から9番目の人と10番目の人の冊数の平均値になります。
9番目は8冊,10番目は10冊なので,第3四分位数は,\( \dfrac{8+10}{2}=9 \)(冊)になります。
(9) 3枚の硬貨を同時に投げるとき,2枚以上裏となる確率を求めなさい。ただし,硬貨は,表と裏のどちらが出ることも同様に確からしいとする。
【解説】
3枚の硬貨に1枚目,2枚目,3枚目 と名前をつけ,
表裏の組み合わせとそれぞれの組み合わせで裏が何枚になるかを樹形図に書きます。
裏が2枚以上になる組み合わせは,
裏が2枚の場合は3通り,3枚の場合は1通りで合計4通り,
すべての組み合わせは8通りなので,
求める確率は,\( \dfrac{4}{8}=\dfrac{1}{2} \)

大問2
紙でふたのない容器をつくるとき,次の(1)から(4)までの各問いに答えなさい。ただし,紙の厚さは考えないものとする。
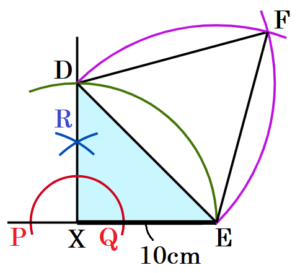
(1) 図1は正三角柱です。底面にあたる正三角形 \( DEF \) の1辺の長さを \( 10\sqrt{2} \; cm \),辺 \( AD \) の長さを \( 10 \; cm \) とする容器をつくります。図2の線分の長さを \( 10 \; cm \) とするとき,底面にあたる正三角形 \( DEF \) をコンパスと定規を使って作図しなさい。 ただし,作図に使った線は消さないこと。

【解答】
手順1 \( 10cm \) の線分の端点を点 \( X \) とし,点 \( X \) を中心に円弧を描く。
(最初の線分とその延長線との交点を点 \( P,Q \) とします。)
手順2 2点 \( P,Q \) を中心に円弧を描く。
(交点を点 \( R \) とします。)
手順3 2点 \( X,R \) を通る直線を描く。
手順4 点 \( X \) を中心に \( 10cm \) の線分を半径とする円弧を描く。
(線分 \( XR \) との交点を点 \( D \) とします。)
ここで,水色の三角形が直角二等辺三角形になるので,斜辺を線分 \( DE \) とします。
手順5 2点 \( D,E \) を中心に線分 \( DR \) を半径とする円弧を描く。
この交点が点 \( F \) となり,正三角形 \( DEF \) ができます。
【解説】
与えられている線分の長さは \( 10 \; cm \),正三角形 \( DEF \) の1辺の長さが \( 10\sqrt{2} \; cm \) なので,
長さの比は \( 1:\sqrt{2} \) であり,与えられている線分を使って直角二等辺三角形を作れば,
斜辺に \( 10\sqrt{2} \; cm \) をつくることができます。
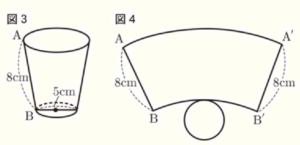
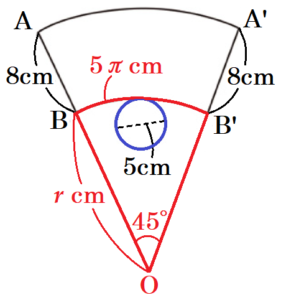
(2) 図3のような紙コップを参考に,容器をつくります。紙コップをひらいたら,図4のような展開図になります。 図4において,側面にあたる辺 \( AB \) と辺 \( A’B’ \) をそれぞれ延ばし,交わった点を \( O \) とすると,弧 \( BB’ \),線分 \( OB \),線分 \( OB’ \) で囲まれる図形が中心角 \( 45° \) のおうぎ形になります。このとき,弧 \( AA’ \) の長さを求めなさい。
【解説】
おうぎ形 \( BOB’ \) の半径を \( r \; cm \) とすると,
弧 \( BB’ \)の長さはコップの底面である直径 \( 5 \; cm \) の円の
円周の長さと等しいので,\( 5\pi{} \; cm \) となります。
おうぎ形の中心角は \( 45° \) なので,
\( 2\pi{}r \times \dfrac{45°}{360°}=5\pi{} \)
\( 2\pi{}r=40\pi{} \)
\( r=20 \; (cm) \)
おうぎ形 \( AOA’ \) は,半径 \( 28 \; cm \),中心角 \( 45° \) なので,
弧 \( AA’=2\pi{} \times 28 \times \dfrac{45°}{360°} \)
\( =7\pi{} \; (cm) \)
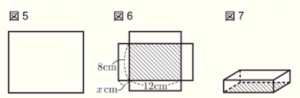
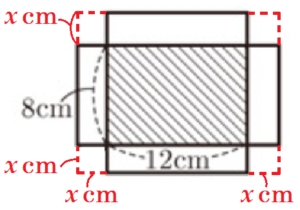
(3) 図5のような,長方形の紙があります。この紙の4すみから,図6のように1辺が,\( x \; cm \) の正方形を切り取り,縦の長さを \( 8 \; cm \),横の長さを \( 12 \; cm \) の長方形を底面とする図7のような直方体をつくります。図5の長方形の紙の面積と,図6の斜線部の長方形の面積の比が,\( 2:1 \) になるとき,\( x \) の長さを求めなさい。ただし,\( x \) の長さを求めるために方程式をつくり,答えを求めるまでの過程も書きなさい。
【解答】
\( (2x+8)(2x+12):8 \times 12=2:1 \)
\( (2x+8)(2x+12)=8 \times 12 \times 2 \)
\( 4(x+4)(x+6)=8 \times 12 \times 2 \)
\( (x+4)(x+6)=48 \)
\( x^2+10x-24=0 \)
\( (x-2)(x+12)=0 \)
\( x=2,-12 \)
\( x>0 \) より,あてはまるのは \( x=2 \)
よって,\( x \) の長さは \( 2 \; cm \)
【解説】
図6において,切り取った正方形を戻し,
図5の紙の縦横の長さを \( x \) を使った式で表すことで,
面積の関係を表す方程式をつくることができます。
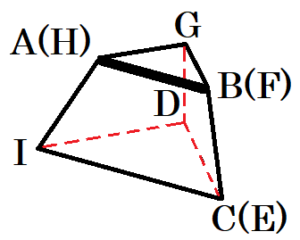
(4) 図8は容器の展開図です。辺 \( AB \),\( IC \) の長さは,それぞれ \( 6 \; cm,12 \; cm \) とします。また,\( DC=DE=DG=DI=HF,GF=GH \),
\( AI=HI=BC=FE,CG⊥HF \),
\( CG⊥IE,AB//IC \) とします。この展開図を組み立てたとき,辺 \( AB \) とねじれの位置にある辺をすべて答えなさい。
ただし,組み立てたときに重なる辺は,どちらか一方の辺を書くこととします。
【解答】
辺 \( CD \),辺 \( DG \),辺 \( DI \)
【解説】
図8の展開図を \( △CDI \) を底面として組み立てると
右の図のようになります。
ねじれの位置にある直線とは
どこまで行っても交わらない直線のうち,平行でないもの
なので,あてはまるのは,\( CD,DG,DI \) になります。
大問3
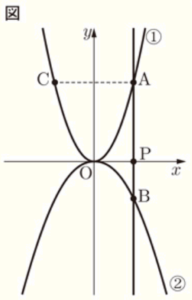
\( y \) が \( x \) の2乗に比例する関数について考えます。下の図において,➀ は関数 \( y=2x^2 \),➁ は \( y=-x^2 \) のグラフです。点 \( P \) は \( x \) 軸上にあり,点 \( P \) の \( x \) 座標を \( t \;\; (t>0) \) とします。点 \( P \) を通り,\( y \) 軸に平行な直線と ➀,➁ のグラフが交わる点を,それぞれ \( A,B \) とします。また,\( y \) 軸について点 \( A \) と対称な点を \( C \) とします。後の(1)から(4)までの各問いに答えなさい。
(1) 関数 \( y=-x^2 \) について,\( x \) の値が \( 1 \) から \( 3 \) まで増加するときの変化の割合を求めなさい。
【解説】
\( x=1 \) のときの \( y \) の値は,\( y=-1 \times 1^2=-1 \)
\( x=3 \) のときの \( y \) の値は,\( y=-1 \times 3^2=-9 \)
なので,
変化の割合 \( =\dfrac{-9-(-1)}{3-1}=-4 \)
(2) 関数 \( y=ax^2 \) のグラフが点 \( (2,2) \) を通るとき,\( a \) の値を求めなさい。また,この関数のグラフをかきなさい。
【解説】
\( y=ax^2 \) に \( x=2,y=2 \) を代入すると,
\( 2=a \times 2^2 \)
\( a=\dfrac{1}{2} \)
\( y=\dfrac{1}{2}x^2 \) のグラフは,点 \( (2,2) \) の他に
\( x=1 \) のとき,\( y=\dfrac{1}{2} \times 1^2=\dfrac{1}{2} \)
\( x=3 \) のとき,\( y=\dfrac{1}{2} \times 3^2=\dfrac{9}{2} \)
\( x=4 \) のとき,\( y=\dfrac{1}{2} \times 4^2=8 \)
\( x=-1 \) のとき,\( y=\dfrac{1}{2} \times (-1)^2=\dfrac{1}{2} \)
\( x=-2 \) のとき,\( y=\dfrac{1}{2} \times (-2)^2=2 \)
\( x=-3 \) のとき,\( y=\dfrac{1}{2} \times (-3)^2=\dfrac{9}{2} \)
\( x=-4 \) のとき,\( y=\dfrac{1}{2} \times (-4)^2=8 \)
を通るのでこれらをつないだ曲線になります。
(3) \( AB+AC \) の長さが \( 1 \) になるときの \( t \) の値を求めなさい。
【解答】
\( t=\dfrac{1}{3} \)
【解説】
点 \( A,B,C \) の座標は,
\( A(t,2t^2),B(t,-t^2),C(-t,2t^2) \)
と表すことができるので,
\( AB=2t^2-(-t^2)=3t^2 \)
\( AC=t-(-t)=2t \)
となります。
よって,
\( AB+AC=1 \)
\( 3t^2+2t=1 \)
\( 3t^2+2t-1=0 \)
\( (3t-1)(t+1)=0 \)
\( t=\dfrac{1}{3},-1 \)
\( t>0 \) より,あてはまるのは,\( t=\dfrac{1}{3} \)
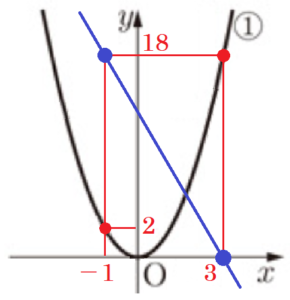
(4) \( x \) の変域が \( -1≦x≦3 \) のとき,関数 \( y=2x^2 \) と \( y=bx+c \;\; (b<0) \) の \( y \) の変域が等しくなります。このとき,\( b,c \) の値を求めなさい。
【解答】
\( b=-\dfrac{9}{2},c=\dfrac{27}{2} \)
【解説】
関数 \( y=2x^2 \) において,\( x \) の変域が \( -1≦x≦3 \) のとき,
\( y \) の変域は,\( 0≦y≦18 \) になります。
次に,\( y=bx+c \;\; (b<0) \) のとき,傾きが負の値なので,
\( x \) の値が大きくなるほど \( y \) の値は小さくなります。
\( y \) の変域が等しくなることから,
\( x=-1 \) のとき \( y=18 \),\( x=3 \) のとき \( y=0 \) になるので,
傾き \( b=\dfrac{0-18}{3-(-1)}=-\dfrac{9}{2} \)
\( y=-\dfrac{9}{2}x+c \) に \( x=3,y=0 \) を代入すると,
\( 0=-\dfrac{9}{2} \times 3+c \)
\( c=\dfrac{27}{2} \)
大問4
\( ∠C=90° \) の直角三角形ABCについて,次の(1),(2)の各問いに答えなさい。
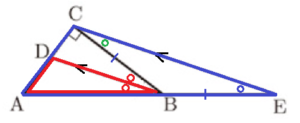
(1) 図1のように,\( ∠B \) の二等分線と辺 \( AC \) の交点を \( D \) とするとき,\( BA:BC=AD:DC \) が成り立つことを証明します。図2のように,点 \( C \) を通り \( DB \) に平行な直線と,辺 \( AB \) を延長した直線との交点を \( E \) とします。図2を使って,\( BA:BC=AD:DC \) を証明しなさい。
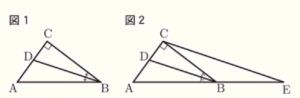
【解答】
\( △ABD \) と \( △AEC \) において,
\( DB//CE \) より,
同位角は等しいので,\( ∠ABD=∠AEC \) ・・・ ①
\( ∠A \) は共通 ・・・ ➁
①➁より,2組の角がそれぞれ等しいので,
\( △ABD \) ∽ \( △AEC \)
相似な三角形の対応する辺の比は等しいので,
\( BA:EA=DA:CA \) であり,\( BA:EB=DA:CD \) ・・・ ➂
また,\( DB//CE \) より,
錯角は等しいので,\( ∠DBC=∠BCE \) ・・・ ➃
➃より,
\( △BCE \) は底角が等しいので,
二等辺三角形であり,\( BE=BC \) ・・・ ➄
➂➄より,\( BA:EB=BA:BC=AD:DC \)
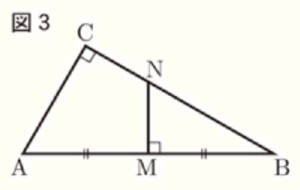
(2) 直角三角形 \( ABC \) の辺 \( AB,CA \) の長さをそれぞれ \( 10,5 \) とします。次の ①,➁ の各問いに答えなさい。
➀ 図3のように,辺 \( AB \) の垂直二等分線をひき,辺 \( AB,BC \) との交点をそれぞれ \( M,N \) とします。
このとき,\( △ABC \) と \( △NBM \) の面積比を求めなさい。
【解説】
\( △ABC \) と \( △NBM \) は,
\( ∠ACB=∠NMB,∠B \) 共通より,
2組の角がそれぞれ等しいので,
\( △ABC \) ∽ \( △NBM \)
\( △ABC \) において,\( AB=10,CA=5 \) より,
\( AB:CA=2:1 \) なので,
\( CB=\sqrt{3}CA=5\sqrt{3} \)
点 \( M \) は \( AB \) の中点なので,\( MB=\dfrac{1}{2}AB=5 \)
よって,\( △ABC \) と \( △NBM \) の相似比は,
\( CB:MB=5\sqrt{3}:5=\sqrt{3}:1 \)
相似な三角形の面積比は相似比の2乗の比になるので,
\( △ABC:△NBM=\sqrt{3}^2:1^2=3:1 \)
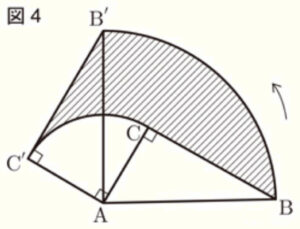
➁ 図4のように,直角三角形 \( △ABC \) を頂点 \( A \) を中心に \( 90° \) 回転させます。このとき,辺 \( BC \) が通過したときにできる斜線部の面積を求めなさい。
【解答】
\( \dfrac{75}{4}\pi{} \)
【解説】
斜線部の面積は,
おうぎ形 \( ABB’+△AB’C’-( \) おうぎ形 \( ACC’+△ABC \; ) \)
で求めることができます。
回転させた前後の図形なので,\( △ABC≡△AB’C’ \) であり,\( △ABC=△AB’C’ \)
ここから,
斜線部の面積 \( = \) おうぎ形 \( ABB’+△AB’C’-( \) おうぎ形 \( ACC’+△ABC \; ) \)
\( = \) おうぎ形 \( ABB’- \) おうぎ形 \( ACC’+△AB’C’-△ABC \)
\( = \) おうぎ形 \( ABB’- \) おうぎ形 \( ACC’ \)
おうぎ形 \( ABB’ \) は,半径 \( 10 \),中心角 \( 90° \) なので,
おうぎ形 \( ABB’=\pi{} \times 10^2 \times \dfrac{90°}{360°}=25\pi{} \)
おうぎ形 \( ACC’ \) は,半径 \( 5 \),中心角 \( 90° \) なので,
おうぎ形 \( ACC’=\pi{} \times 5^2 \times \dfrac{90°}{360°}=\dfrac{25}{4}\pi{} \)
以上より,
斜線部の面積 \( = \) おうぎ形 \( ABB’- \) おうぎ形 \( ACC’ \)
\( =25\pi{}-\dfrac{25}{4}\pi{} \)
\( =\dfrac{75}{4}\pi{} \)












-アイキャッチ-120x68.jpg)