大問１
次の(1)～(8)の問いに答えなさい。
(1) \( 7-(-3)-3 \) を計算しなさい。
(2) \( 2(3a-2b)-4(2a-3b) \) を計算しなさい。
(3) \( (-6ab)^2÷4ab^2 \) を計算しなさい。
(4) 連立方程式 \( \left\{
\begin{array}{}
x+3y=21 \\
2x-y=7
\end{array}
\right. \) を解きなさい。
(5) \( \sqrt{45}-\sqrt{5}+\dfrac{10}{\sqrt{5}} \) を計算しなさい。
(6) １３０人の生徒が１人 \( a \) 円ずつ出して、1つ \( b \) 円の花束を５つと、１本１５０円のボールペンを５本買って代金を払うと，おつりがあった。このとき，数量の関係を不等式で表しなさい。
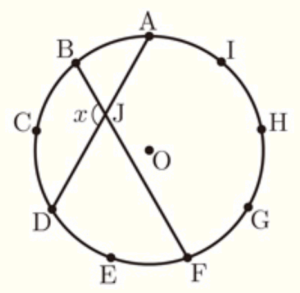
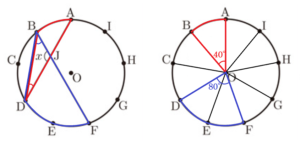
(7) 右の図のように，円 \( O \) の周上に円周を９等分する
９つの点 \( A，B，C，D，E，F，G，H，I \) がある。
線分 \( AD \) と線分 \( BF \) の交点を \( J \) とするとき，
\( ∠x \) の大きさを答えなさい。
\( A \) ～ \( I \) の各点から中心 \( O \) に補助線を引くと，\( A \) ～ \( I \) は円周を９等分した点なので，
それぞれのおうぎ形の中心角は， \( 360° \div 9=40° \) になります。
弧 \( AB \) の中心角 \( ∠AOB=40° \) なので，円周角 \( ∠ADB=20° \)
弧 \( DF \) の中心角 \( ∠DOF=80° \) なので，円周角 \( ∠DBF=40° \)
よって，
\( ∠x=180°-(∠ADB+∠DBF) \)
\( =180°-(20°+40°)=120° \)
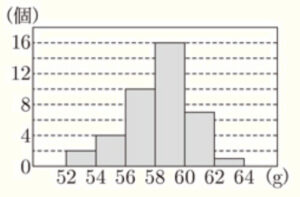
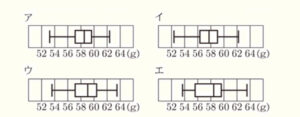
(8) 右の図は，ある家庭で購入した卵４０個の重さを１個ずつはかり，ヒストグラムに表したものである。このヒストグラムに対応する箱ひげ図として正しいものを，次のア〜エから１つ選び，その符号を書きなさい。ただし，階級は５２ｇ以上５４ｇ未満のように，２ｇごとの区間に区切っている。
大問２
次の(1)～(3)の問いに答えなさい。
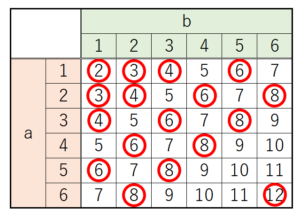
(1) １から６までの目のついた１つのさいころを２回投げるとき，１回目に出る目の数を \( a \) ，２回目に出る目の数を \( b \) とする。このとき， \( \dfrac{24}{a+b} \) が整数になる確率を求めなさい。
２４の約数は， \( 1，2，3，4，6，8，12，24 \) です。
\( a，b \) それぞれの値に対して\( a+b \) がいくつになるかを表に書いて，
２４の約数であるマスに○をつけます。
すべての場合の数が３６マス，○がついたマスは１７マスなので，
求める確率は，\( \dfrac{17}{36} \)
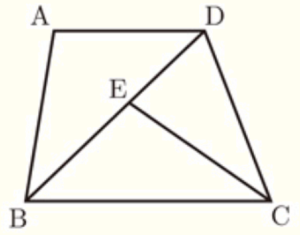
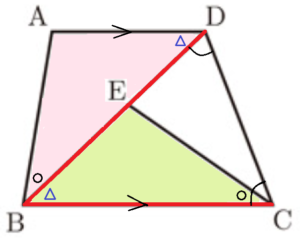
(2) 右の図のように，\( AD/\!/BC \) の台形 \( ABCD \) があり，\( ∠BCD=∠BDC \) である。対角線 \( BD \) 上に，\( ∠DBA=∠BCE \) となる点 \( E \) をとるとき，\( AB=EC \) であることを証明しなさい。
\( △ABD \) と \( △ECB \) において，
\( ∠BCD=∠BDC \) より，\( △BCD \) は二等辺三角形で，
\( BD=BC\) ･･･ ①
仮定より，\( ∠DBA=∠BCE \) ･･･ ➁
\( AD/\!/BC \)より，錯角は等しいので，\( ∠ADB=∠EBC \) ･･･ ➂
①②③より，１組の辺の長さとその両端の角の大きさが等しいので，
\( △ABD≡△ECB \)
よって，対応する辺の長さは等しいので，\( AB=EC \)
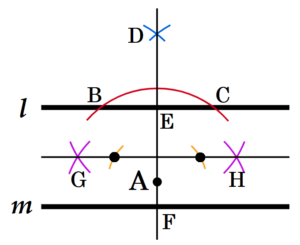
(3) 右の図のように，平行な２直線 \( l，m \) と点 \( A \) がある。点 \( A \) を通り，２直線 \( l，m \) の両方に接する円の中心を，定規とコンパスを用いて，作図によってすべて求め，それらの点に・をつけなさい。ただし，作図に使った線は消さないで残しておくこと。
直線 \( l，m \) と平行でちょうど真ん中にある直線上にあります。
点 \( A \) をはさんで両側にあることに注意しましょう。
手順１ 点 \( A \) を中心に，直線 \( l \) と交わるような弧を描く。
（交点を点 \( B，C \) とします）
手順２ 点 \( B，C \) を中心に，弧を描く。
（交点を点 \( D \) とします）
手順３ 点 \( A，D \) を通る直線を描く。
（直線 \( l，m \) との交点を点 \( E，F \) とします）
手順４ 点 \( E，F \) を中心に，弧を描く。
（交点を点 \( G，H \) とします）
手順５ 点 \( G，H \) を通る直線を描く。
手順６ 点 \( A \) を中心に，手順５の直線と交わるような弧を描く。
大問３
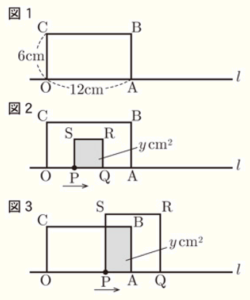
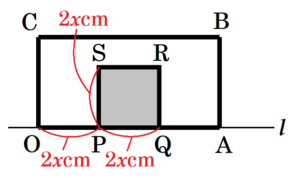
右の図１のように， \( OA=12 cm，OC=6cm \) の長方形 \( OABC \) があり，２つの頂点 \( O，A \) は直線 \( l \) 上にある。点 \( P \) は，頂点 \( O \) を出発し，每秒 \( 2 \: cm \) の速さで，図２，３のように直線 \( l \) 上を頂点 \( A \) まで移動する。また，線分 \( OP \) の延長上に， \( OP=PQ \) となる点 \( Q \) をとり，直線 \( l \) について長方形 \( OABC \) と同じ側に，正方形 \( PQRS \) をつくる。
点 \( P \) が頂点 \( O \) を出発してから，\(x\) 秒後の長方形 \( OABC \) と正方形 \( PQRS \) の重なっている部分の面積を \( y \: cm^2 \) とするとき，次の(1)～(4)の問いに答えなさい。ただし，点 \( P \) が 頂点 \( O，A \) にあるときは，\( y=0 \) とする。
(1) \( x=2 \) のとき，\( y \) の値を答えなさい。
\( x=2 \) のとき，\( OP=4 \: cm \) なので，
正方形 \( PQRS \) は，１辺 \( 4 \: cm \) 。
よって，\( y=4 \times 4=16 \)
(2) 次の①，②について，\( y \) を \( x \) の式で表しなさい。
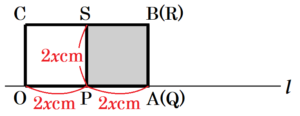
① \( 0≦x≦3 \) のとき
この範囲では，正方形 \( PQRS \) は長方形 \( OABC \) の内側でだんだん大きくなっていきます。
右の図は \( x=3 \) のときのもので，
\( OP=PQ=PS=6 \: cm \)となり，
長方形 \( OABC \) のちょうど半分になります。
よって，\( y=2x \times 2x=4x^2 \)
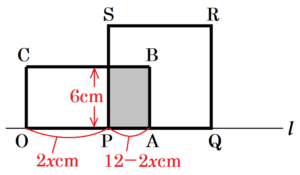
② \( 3≦x≦6 \) のとき
この範囲では，点 \( Q \) は点 \( A \) より右側にあるので，正方形 \( PQRS \) の一部だけが長方形 \( OABC \) と重なります。
\(x\) 秒後，\( OP=2x \: cm \) なので，\( PA=12-2x \: cm \)，
重なっている部分の高さは \( 6 \: cm \) で一定なので，
\( y=(12-2x) \times 6=-12x+72 \)
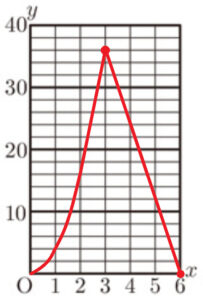
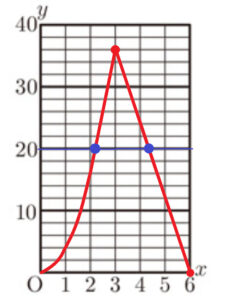
(3) \( 0≦x≦6 \) のとき，\( x \) と \( y \) の関係を表すグラフをかきなさい。
(2) より，\( x \) と \( y \) の関係は，
\( 0≦x≦3 \) のとき \( y=4x^2 \)
\( 3≦x≦6 \) のとき \( y=-12x+72 \)
\( x=3 \) のとき，\( y \) 座標の値は
\( y=4 \times 3^2=36 \)
また，\( y \) 座標が \( 0 \) になるときの
\( y \) 座標の値は，
\( 0=-12x+72 \)
\( 12x=72 \)
\( x=6 \)
(4) \( y=20 \) となる \( x \) の値をすべて求めなさい。
\( y=20 \) となるのは，右のグラフで ● のところです。
\( 0≦x≦3 \) のとき
\( 20=4x^2 \)
\( x^2=5 \)
\( x= \sqrt{5} \) ( \(x≧0 \) より )
\( 3≦x≦6 \) のとき
\( 20=-12x+72 \)
\( 12x=52 \)
\( x= \dfrac{13}{3} \)
大問４
箱の中に、数字を書いた １０枚のカード， \( \fbox{0}，\fbox{1}，\fbox{2}，\fbox{3}，\fbox{4}，\fbox{5}，\fbox{6}，\fbox{7}，\fbox{8}，\fbox{9} \) が入っている。これらのカードを使い、次の手順Ⅰ～Ⅲ に従って，下のような記録用紙に数を記入していく。このとき，あとの (1)，(2) の問いに答えなさい。
手順
I 箱の中から１枚のカードを取り出して、そのカードに書かれている数字を，記録用紙の１番目の欄に記入し，カードを箱の中に戻す。
Ⅱ 箱の中からもう一度１枚のカードを取り出して，そのカードに書かれている数字を，記録用紙の２番目の欄に記入し，カードを箱の中に戻す。
Ⅲ 次に，記録用紙の \( (n-2) \) 番目の欄の数と \( (n-1) \) 番目の欄の数の和を求め，その一の位の数を \( n \) 番目の欄に記入する。ただし， \( n \) は３以上１８以下の自然数とする。
(1) 次の文は，手順Ⅰ～Ⅲに従って，記録用紙に数を記入するときの例について述べたものである。このとき，文中の ア ～ ウ に当てはまる数を，それぞれ答えなさい。
例えば、手順Ⅰで２のカード，手順Ⅱで３のカードを取り出したときには，下のように，記録用紙の１番目の欄には２，２番目の欄には３を記入する。このとき，１６番目の欄に記入する数は ア ，１７番目の欄に記入する数は イ ，１８番目の欄に記入する数は ウ となる。
(2) 手順 I，Ⅱで取り出したカードに書かれている数字と，手順Ⅲで記録用紙に記入する数に，どのような関係があるかを調べるために，次の表１，２を作った。
表１は，手順Ⅰで \( \fbox{0} \) ～ \( \fbox{9} \) のいずれか１枚のカードを取り出し，手順Ⅱで \( \fbox{5} \) のカードを取り出したときのそれぞれの場合について，１番目の欄の数を小さい順に並べ替えてまとめたものである。また，表２は，手順Ⅰで \( \fbox{0} \) ～ \( \fbox{9} \) のいずれか１枚のカードを取り出し，手順Ⅱで \( \fbox{6} \) のカードを取り出したときのそれぞれの場合について，１番目の欄の数を小さい順に並べ替えてまとめたものである。このとき，あとの①，②の問いに答えなさい。
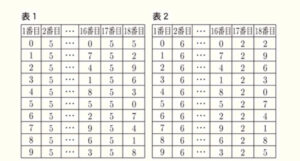
① 手順Ⅱで \( \fbox{5} \) ， \( \fbox{6} \) 以外のカードを取り出しても，１７番目の欄の数は，１番目の欄の数に関係なく，２番目の欄の数によって決まる。このことを証明しなさい。
② 手順Ⅰで \( \fbox{x} \) のカード，手順Ⅱで \( \fbox{4} \) のカードを取り出したとき，１８番目の欄の数が１になった。このとき，\( x \) の値を求めなさい。
\( 987a+1597b=98 \times 10a+159 \times 10b+7(a+b) \) より，
\( 7a+7b \) の一の位の数と等しくなるので， \( a=x，b=4 \) を代入すると，\( 7x+28 \)
\( 7x+28 \) の一の位の数が１になるということは，
\( 7x \) の一の位は３なので，
あてはまるのは，\(7 \times 9=63 \) の場合のみです。
よって， \( x=9 \)
大問５
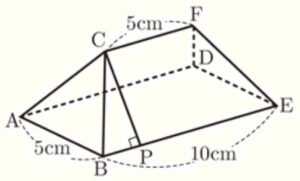
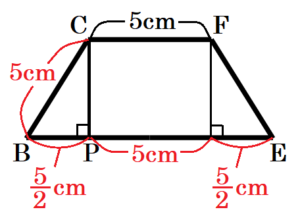
右の図のような立体 \( ABC－DEF \) があり，四角形 \( ABED \) は，\( BA=5 \: cm，BE=10 \: cm \) の長方形であり，\( △ABC \) と \( △DEF \) は正三角形である。また，辺 \( BE \) と辺 \( CF \) は平行であり， \( CF=5 \: cm \) である。点 \( C \) から辺 \( BE \) に引いた垂線と辺 \( BE \) との交点を \( P \) とするとき、次の (1)～(3) の問いに答えなさい。
(1) 線分 \( CP \) の長さを答えなさい。
\( △ABC \) と \( △DEF \) はともに１辺 \( 5 \: cm \) の正三角形で，
面 \( BEFC \) は等脚台形なので，\( △BCP \) において三平方の定理より，
\( CP^2=BC^2-BP^2 \)
\( =5^2-\dfrac{5}{2}^2 \)
\( =\dfrac{75}{4} \)
\( CP=\dfrac{ \sqrt{75}}{2}=\dfrac{ 5\sqrt{3}}{2} \)
(2) ５点 \( C，A，B，E，D \) を結んでできる四角すいの体積を求めなさい。
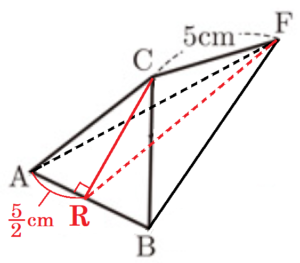
(3) ４点 \( A，B，C，F \) を結んでできる三角すいの体積を求めなさい。
右の図は，問題の図から求める三角すいだけを取り出したものです。
辺 \( AB \) の中点を \( R \) とし，面 \( CFR \) で切断すると，
求める三角すい＝ \(2\) 三角すい \( A－CFR \) になります。
よって，求める三角すいの体積は，
\( △CFR \times AR \times \dfrac{1}{3} \times 2 \)
\( =\left( 5 \times \dfrac{ 5\sqrt{2}}{2} \times \dfrac{1}{2} \right) \times \dfrac{5}{2} \times \dfrac{1}{3} \times 2 \)
\( =\dfrac{125\sqrt{2}}{12} (cm^3) \)
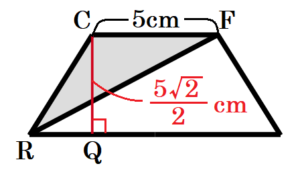
【補足： \( △CFR \) の求め方】
辺 \( CF \) を通り面 \( ABED \) に垂直な面でこの立体を切ると，
切断面は右の図のようになります。
(2)で利用した点 \( Q \) は，この面上にあるので，
\( △CFR=CF \times CQ \times \dfrac{1}{2} \)
\( =5 \times \dfrac{ 5\sqrt{2}}{2} \times \dfrac{1}{2} \)
