大問1
(1) \( -2+7 \) を計算しなさい。
(2) \( -\dfrac{3}{4}×\dfrac{2}{15} \) を計算しなさい。
【解答】
\( -\dfrac{1}{10} \)
【解説】
\( =-\dfrac{3 \times 2}{4 \times 15} \)
\( =-\dfrac{1}{10} \)
(3) \( \sqrt{50}+ \sqrt{8}- \sqrt{18} \) を計算しなさい。
【解説】
\( =5\sqrt{2}+2\sqrt{2}-3\sqrt{2} \)
\( =4\sqrt{2} \)
(4) 等式 \( -a+3b=1 \) を,\( b \) について解きなさい。
【解答】
\( b=\dfrac{a+1}{3} \)
【解説】
\( 3b=a+1 \)
\( b=\dfrac{a+1}{3} \)
(5) 連立方程式 \( \left\{ \begin{array}{}
y=x-6 \\
3x+4y=11
\end{array} \right. \) を解きなさい。
【解説】
\( y=x-6 \) ・・・ ①
\( 3x+4y=11 \) ・・・ ②
①を②に代入
\( 3x+4(x-6)=11 \)
\( 3x+4x-24=11 \)
\( 7x=35 \)
\( x=5 \)
①に代入
\( y=5-6=-1 \)
(6) 二次方程式 \( 9x^2=5x \) を解きなさい。
【解答】
\( x=0,\dfrac{5}{9} \)
【解説】
\( 9x^2-5x=0 \)
\( x(9x-5)=0 \)
\( x=0,\dfrac{5}{9} \)
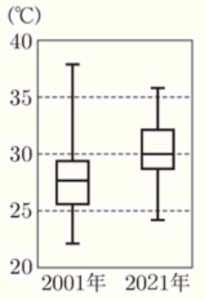
(7) 右の図は,ある地域の2001年と2021年の9月の「日最高気温」を箱ひげ図に表したものである。
この箱ひげ図から読みとれることとして,正しいといえることを,次のア〜エから1つ選び,記号で答えなさい。
ア 2001年では,半分以上の日が30℃以上である。
イ 2021年では,平均値が30℃である。
ウ 気温が25℃以下の日は,2021年より2001年の方が多い。
エ 気温の散らばりの程度は,2001年より2021年の方が小さい。
【解説】
ア 2001年は,第三四分位数が30℃未満なので,30℃以上の日は7日以下。
イ 2021年では,中央値が30℃である。
ウ この箱ひげ図だけでは判断ができない。
(反例) 2001年は22℃が1日,26℃が6日,2021年は24℃が7日 もあり得る
エ データの範囲(最大値と最小値の差)と四分位範囲(第三四分位数と第一四分位数の差)が
どちらも2021年の方が小さい。
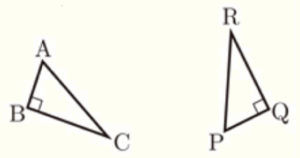
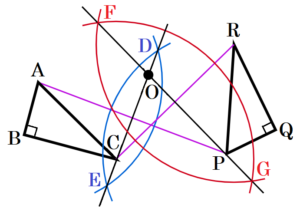
(8) 右の図で,\( △PQR \) は,\( △ABC \) を回転移動したものである。このとき,回転の中心である点 \( O \) をコンパスと定規を使って作図しなさい。作図に用いた線は消さずに残しておくこと。
【解答・解説】
\( △PQR \) は,\( △ABC \) を回転移動したものということは,\( △PQR≡△ABC \) なので,
\( OA=OP,OB=OQ,OC=OR \) になります。
よって,点 \( O \) は,線分 \( AP \),線分 \( BQ \),線分 \( CR \),それぞれの垂直二等分線の交点になります。
手順1 線分 \( AP \),線分 \( CR \) を引く
手順2 点 \( A,P \) を中心に円弧を描く
(交点を点 \( D,E \) とします。)
手順3 点 \( D,E \) を通る直線を描く
手順4 点 \( C,R \) を中心に円弧を描く
(交点を点 \( F,G \) とします。)
手順5 点 \( F,G \) を通る直線を描く
手順2と手順5の直線の交点が点 \( O \) になります。
大問2
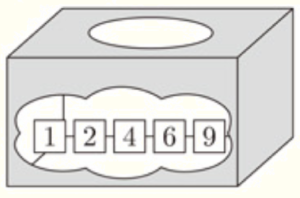
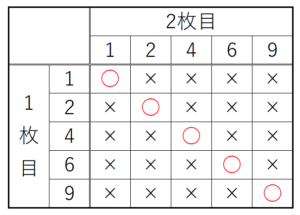
1 右の図のような, \( 1,2,4,6,9 \) の数字が書かれたカードがそれぞれ1枚ずつはいっている箱がある。最初に箱からカードを1枚取り出し,数字を確認した後,箱の中にもどす。次に,箱の中のカードをよくかき混ぜて,もう一度箱の中からカードを1枚取り出し,数字を確認する。
このとき,次の (1) ,(2) の問いに答えなさい。
ただし,どのカードが取り出されることも同様に確からしいとする。
(1) 最初に取り出したカードに書かれた数字と,次に取り出したカードに書かれた数字が同じである確率を求めなさい。
【解説】
取り出したカードの組み合わせを表に表し,同じ数字になるところに
○をつけてみます。
すべての組み合わせは25通りで,同じ数字になるのは5通りなので,
求める確率は,\( \dfrac{5}{25}=\dfrac{1}{5} \)
(2) 最初に取り出したカードに書かれた数字を十の位,次に取り出したカードに書かれた数字を一の位とし,2けたの整数をつくる。
このとき,次のアとイでは,どちらの方が起こりやすいといえるか、確率を使って説明しなさい。
ア 2けたの整数が,4の倍数になる
イ 2けたの整数が,6の倍数になる
【解答】
2けたの整数が,4の倍数になる確率は \( \dfrac{7}{25} \),6の倍数になる確率は \( \dfrac{1}{5} \)なので,
「ア 2けたの整数が,4の倍数になる」方が起こりやすいといえる。
【解説】
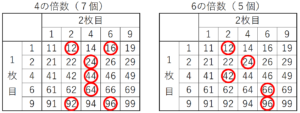
取り出したカードの組み合わせでできる2けたの整数を表に表し,
4の倍数,6の倍数になるところに
○をつけてみます。
2 亮太さんと洋子さんは,農場の体験活動で収穫したじゃがいもと玉ねぎを使って,カレーと肉じゃがをつくることにした。図は,カレーと肉じゃがの主な材料と分量をインターネットを活用して調べたものである。また,【会話】は,2人が何人分の料理をつくることができるか話し合っている場面である。
このとき,下の (1) ,(2) の問いに答えなさい。

【会話】
亮太:収穫した野菜の重さを量ってみたら,じゃがいもの重さの合計は \( 1120 \; g \),玉ねぎの重さの
合計は \( 820 \; g \) だったよ。
洋子:調べた分量で,カレーと肉じゃがを両方つくるとすると,それぞれ何人分できるかな。
亮太:カレーを \( x \) 人分,肉じゃがを \( y \) 人分つくると考えると,使用するじゃがいもの重さの
合計は \( 100x+600y \; (g) \) になるね。
洋子:ちょっと待って。図の中に書いてある人数をよく見てみようよ。
亮太:あっ,式がまちがっているね。正しい式は \( (g) \) になるね。
洋子:そうだね。さっき量ったじゃがいもと玉ねぎを全部使って,カレーと肉じゃがを両方つくるとき,
カレーは ① 人分,肉じゃがは ② 人分できるね。
(1) 【会話】の中で,亮太さんは 部の式がまちがっていることに気づいた。
に当てはまる式を答えなさい。
【解説】
図に書かれているじゃがいもの分量は,カレーの場合は2人分,肉じゃがの場合は5人分なので,
1人分に必要なじゃがいもの量は,カレーは50g, 肉じゃがは120g。
(2) 【会話】の ① , ② に当てはまる数を答えなさい。
【解答】
① ・・・ \( 8 \)
② ・・・ \( 6 \)
【解説】
じゃがいもの分量について方程式をつくると,
\( 50x+120y=1120 \) ・・・ ①
玉ねぎの分量についても,方程式をつくると,
1人分に必要な玉ねぎの量は,カレーは65g, 肉じゃがは50g なので,
\( 65x+50y=820 \) ・・・ ②
①➁を連立方程式として解くと,
\( x=8,y=6 \)
\( \left\{ \begin{array}{}
50x+120y=1120 \\
65x+50y=820
\end{array} \right. \)
①\( \times 5 \)
\( 250x+600y=5600 \) ・・・ ➀’
➁\( \times 12 \)
\( 780x+600y=9840 \) ・・・ ➁’
➁’\(-\)➀’
\( 530x=4240 \)
\( x=8 \)
➀に代入
\( 50 \times 8+120y=1120 \)
\( 120y=720 \)
\( y=6 \)
大問3
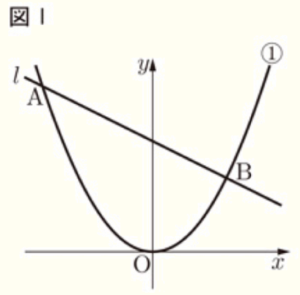
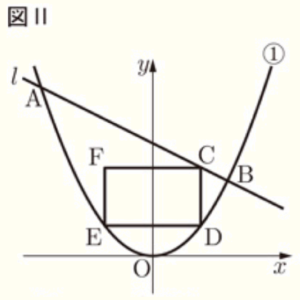
図Ⅰのように,関数 \( y=\dfrac{1}{4}x^2 \) ・・・ ➀ のグラフと直線 \( l \) が2点 \( A,B \) で交わり,点 \( A,B \) の \( x \) 座標は,それぞれ \( -6,4 \) である。
このとき,次の1~3の問いに答えなさい。
1 点 \( A \) の \( y \) 座標を求めなさい。
【解説】
点 \( A \) の \( x \) 座標は,\( -6 \) なので,
\( y=\dfrac{1}{4} \times (-6)^2=9 \)
2 直線 \( l \) の式を求めなさい。
【解答】
\( y=-\dfrac{1}{2}x+6 \)
【解説】
点 \( B \) の \( x \) 座標は,\( 4 \) なので,
\( y=\dfrac{1}{4} \times 4^2=4 \)
直線 \( l \) は, \( A(-6,9),B(4,4) \) を通る直線なので,
傾き \( =\dfrac{4-9}{4-(-6)}=-\dfrac{1}{2} \)
直線 \( l \) の式を \( y=-\dfrac{1}{2}x+b \) とし,
\( x=4,y=4 \) を代入すると,
\( 4=-\dfrac{1}{2} \times 4+b \)
\( 4=-2+b \)
\( b=6 \)
以上より,直線 \( l \) の式は,\( y=-\dfrac{1}{2}x+6 \)
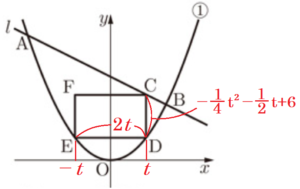
3 図Ⅱは,図Ⅰにおいて,直線 \( l \) 上に点 \( C \) をとり,点 \( C \) を通り \( y \) 軸に平行な直線と①のグラフの交点を \( D \),点 \( D \) を通り \( x \) 軸に平行な直線と①のグラフの交点を \( E \) とし,長方形 \( CDEF \) をつくったものである。
ただし,点 \( C \) の \( x \) 座標を \( t \) とし,\( t \) の変域は \( 0<t<4 \) とする。
このとき,次の (1) ,(2) の問いに答えなさい。
(1) 線分 \( CD \) の長さを,\( t \) を用いて表しなさい。
【解答】
\( -\dfrac{1}{4}t^2-\dfrac{1}{2}t+6 \)
【解説】
点 \( C \) は,直線 \( l \) 上の点なので,\( y \) 座標の値は,
\( y=-\dfrac{1}{2}t+6 \)
点 \( D \) は,関数 \( y=\dfrac{1}{4}x^2 \) 上の点なので,
\( y \) 座標の値は,\( y=\dfrac{1}{4}t^2 \)
よって,線分 \( CD \) の長さは,
\( CD= \) [点 \( C \) の \( y \) 座標]\(-\)[点 \( D \) の \( y \) 座標]
\( =-\dfrac{1}{2}t+6-\dfrac{1}{4}t^2 \)
\( =-\dfrac{1}{4}t^2-\dfrac{1}{2}t+6 \)
(2) 長方形 \( CDEF \) が正方形となるとき,点 \( C \) の座標を求めなさい。
【解説】
関数 \( y=\dfrac{1}{4}x^2 \) のグラフは
\( y \) 軸に対して対称な形になっているので,
点 \( D \) と点 \( E \) の \( y \) 座標の値が等しい
ということは,\( x \) 座標の絶対値が等しいということになります。
よって,点 \( E \) の \( x \) 座標の値は \( -t \) になります。
このとき,線分 \( DE \) の長さは,\( 2t \) になります。
正方形は4辺の長さがすべて等しいので,
\( CD=DE \)
\( -\dfrac{1}{4}t^2-\dfrac{1}{2}t+6=2t \)
これを解くと,
\( t=2 \) ( \( 0<t<4 \) より)
\( x \) 座標が \( 2 \) のときの点 \( C \) の \( y \) 座標の値は,
\( y=-\dfrac{1}{2} \times 2+6=5 \)
以上より,\( C(2,5) \)
● 方程式の解法(途中式)
\( -\dfrac{1}{4}t^2-\dfrac{1}{2}t+6=2t \)
\( t^2+2t-24=-8t \)
\( t^2+10t-24=0 \)
\( (t-2)(t+12)=0 \)
\( t=2 \) ( \( 0<t<4 \) より)
大問4
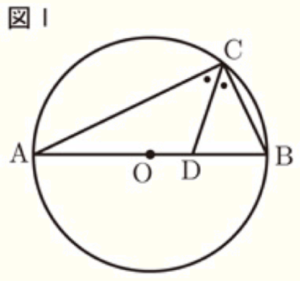
図Ⅰのように,線分 \( AB \) を直径とする円 \( O \) の円周上に点 \( C \) をとり,\( △ABC \) をつくる。\( ∠C \) の二等分線と辺 \( AB \) との交点を \( D \) とする。
このとき,次の1,2の問いに答えなさい。
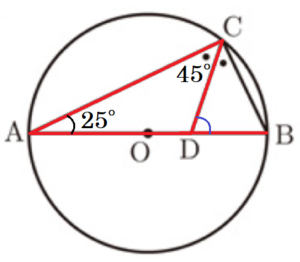
1 \( ∠CAB=25° \) のとき,\( ∠CDB \) の大きさを求めなさい。
【解説】
\( ∠ACB \) は直径 \( AB \) に対する円周角なので,
\( ∠ACB=90° \)
線分 \( CD \) は \( ∠ACB \) の二等分線なので,
\( ∠ACD=45° \)
\( ∠CDB \) は \( △ACD \) の外角なので,
\( ∠CDB=∠CAD+∠ACD=70° \)
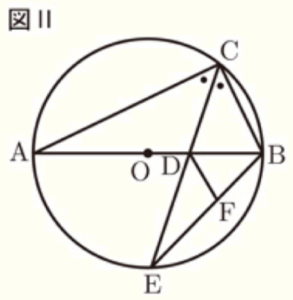
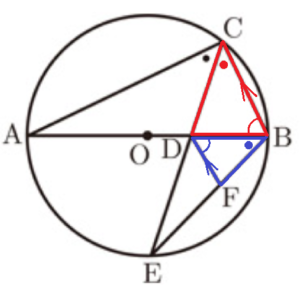
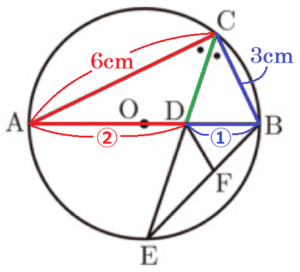
2 図Ⅱは,図Ⅰにおいて,線分 \( CD \) を延長した直線と円 \( O \) との交点を \( E \) とし,線分 \( BE \) 上に \( CB//DF \) となる点 \( F \) をとったものである。
\( AC=6 \; cm,BC=3 \; cm \) とするとき,次の (1)~(3) の問いに答えなさい。
(1) \( △BCD \)∽\( △DBF \) であることを証明しなさい。
【解答・解説】
\( △BCD \)と\( △DBF \) において,
線分 \( CD \) は \( ∠ACB \) の二等分線なので,
\( ∠ACD=∠BCD \) ・・・ ➀
弧 \( AE \) の円周角なので,
\( ∠ACD=∠DBF \) ・・・ ➁
➀➁より,
\( ∠BCD=∠DBF \) ・・・ ➂
\( CB//DF \) より,錯角は等しいので,
\( ∠CBD=∠BDF \) ・・・ ➃
➂➃より,2組の角がそれぞれ等しいので,\( △BCD \)∽\( △DBF \)
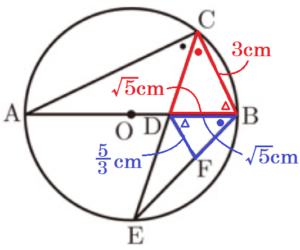
(2) 線分 \( DB \) の長さを求めなさい。
【解答】
\( \sqrt{5} \; cm \)
【解説】
\( △ACB \) は直角三角形なので,三平方の定理より,
\( AB^2=AC^2+BC^2 \)
\( =6^2+3^2 \)
\( =45 \)
\( AB=3\sqrt{5} \; (cm) \) ( \( AB>0 \) より)
線分 \( CD \) は \( ∠ACB \) の二等分線なので,
\( AD:DB=AC:BC=6:3=2:1 \)
よって,
\( DB=\dfrac{1}{3}AB \)
\( =\dfrac{1}{3} \times 3\sqrt{5} \)
\( =\sqrt{5} \; (cm) \)
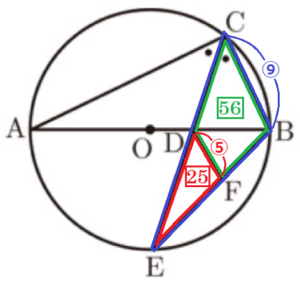
(3) \( △DEF \) の面積を求めなさい。
【解答】
\( \dfrac{25}{12} \; cm^2 \)
【解説】
(1) より,\( △BCD \)∽\( △DBF \) であり,
相似比は,\( BC:DB=3:\sqrt{5} \)
相似な三角形の面積比は相似比の2乗の比になるので,
\( △BCD:△DBF=3^2:\sqrt{5}^2=9:5 \)
\( △DBF=\dfrac{5}{9}△BCD \) ・・・ ➀
また,相似な三角形の対応する辺の比は等しいので
\( BC:DB=BD:DF \)
\( 3:\sqrt{5}=\sqrt{5}:DF \)
\( DF=\dfrac{5}{3} \; (cm) \)
\( CB//DF \) より,\( △DEF \)∽\( △CEB \) なので,
\( CB:DF=3:\dfrac{5}{3}=9:5 \)
相似な三角形の面積比は相似比の2乗の比になるので,
\( △DEF:△CEB=5^2:9^2=25:81 \)
四角形 \( BCDF=△CEB-△DEF \) より,
\( △DEF: \) 四角形 \( BCDF=25:(81-25)=25:56 \)
\( △DEF=\dfrac{25}{56} \) 四角形 \( BCDF \) ・・・ ➁
\( △ABC=AC \times BC \times \dfrac{1}{2}=9 \; (cm^2) \),\( AD:DB=2:1 \) より,
\( △BCD=\dfrac{1}{3}△ABC=3 \; (cm^2) \)
➀より,
\( △DBF=\dfrac{5}{9}△BCD=\dfrac{5}{3} \; (cm^2) \)
四角形 \( BCDF=△BCD+△DBF=3+\dfrac{5}{3}=\dfrac{14}{3} \; (cm^2) \)
➁より,
\( △DEF=\dfrac{25}{56} \) 四角形 \( BCDF=\dfrac{25}{12} \; (cm^2) \)
大問5
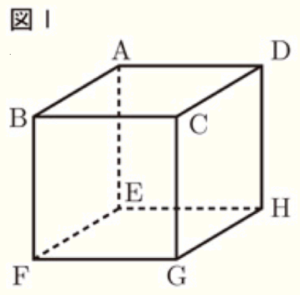
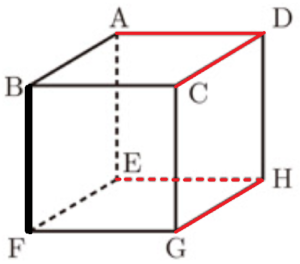
図Ⅰのような1辺の長さが \( 6 \; cm \) の立方体がある。
このとき,次の1~4の問いに答えなさい。
1 図Ⅰにおいて,辺を直線とみたとき,直線 \( BF \) とねじれの位置にある直線は何本あるか答えなさい。
【解説】
直線 \( BF \) とねじれの位置にある直線は
\( AD,CD,EH,GH \) の4本
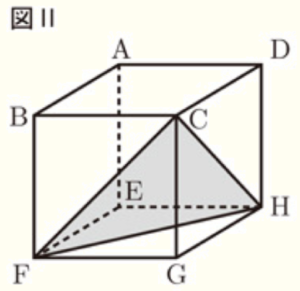
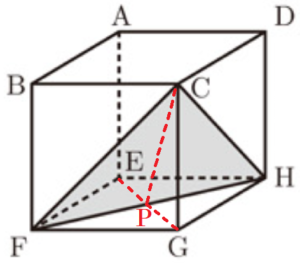
2 図Ⅱは,図Ⅰにおいて,3点 \( C,F,H \) を頂点とする \( △CFH \) を示したものである。この \( △CFH \) の面積を求めなさい。
【解答】
\( 18 \sqrt{3} \; cm^2 \)
【解説】
線分 \( FH \) と線分 \( EG \) の交点を点 \( P \) とすると,
\( △CFH=FH \times CP \times \dfrac{1}{2} \)
で求めることができます。
面 \( EFGH \) は正方形なので,
\( EF=FG=6 \; cm \) より,
\( EG= \sqrt{2}FG=6\sqrt{2} \; (cm) \)
正方形の対角線はそれぞれの中点で交わるので,
\( PG=\dfrac{1}{2}EG=3\sqrt{2} \; (cm) \)
\( △CPG \) において,三平方の定理より,
\( CP^2=CG^2+PG^2=54 \)
\( CP=3 \sqrt{6} \; (cm) \) (\(CP>0\) より)
よって,
\( △CFH=FH \times CP \times \dfrac{1}{2} \)
\( =6\sqrt{2} \times 3 \sqrt{6} \times \dfrac{1}{2} \)
\( =18\sqrt{3} \; (cm^2) \)
【線分 \( CP \) が \( △CFH \) の高さになる理由】
\( CF=CH,FP=HP,CP \) は共通 より,
\( △CFP≡△CHP \)
よって,\( ∠CPF=∠CPH \)
3点 \( F,P,H \) は一直線上にあるので,
\( ∠CPF=∠CPH=\dfrac{180°}{2}=90° \)
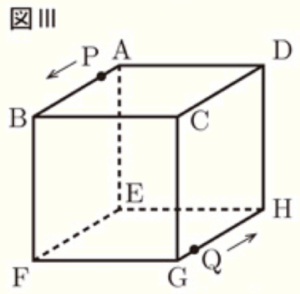
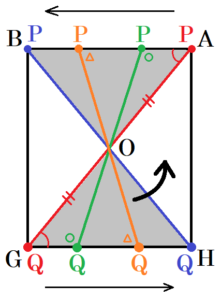
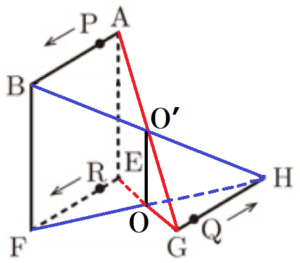
3 図Ⅲは,図Ⅰにおいて,頂点 \( A \) を出発して,頂点 \( B \) まで動く点 \( P \) と,頂点 \( G \) を出発して,頂点 \( H \) まで動く点 \( Q \) を示したものである。点 \( P,Q \) は,それぞれ頂点 \( A,G \) を同時に出発して,頂点 \( B,H \) まで同じ速さで動く。
このとき,線分 \( PQ \) が動いてできる図形の面積を求めなさい。
【解答】
\( 18 \sqrt{2} \; cm^2 \)
【解説】
線分 \( PQ \) が,赤→緑→オレンジ→青 と進んでいくとすると,
線分 \( PQ \) が動いてできる図形は右の図で灰色の部分になります。
このとき,線分 \( PQ \) は必ず 線分 \( AG \) の中点を通っています。
なぜ中点を通るっていえるの?
線分 \( AG \) と線分 \( PQ \) の交点を点 \( O \) とすると,
点 \( P,Q \) は,同じ速さで動くので,\( AP=GQ \)
\( AB//GH \) なので,\( ∠PAO=∠QGO,∠APO=∠GQO \)
よって,1組の辺とその両端の角がそれぞれ等しいので,
\( △APO≡△GQO \)
ここから,線分 \( PQ \) は必ず 線分 \( AG \) の中点を通っています。
\( AO=GO \) より,\( △AOH=△GOH \) なので,
\( △GOH \) の部分の面積を \( △AOH \) に移すと,
\( △ABH \) の面積と等しくなっています。
よって,求める面積は,
\( AB \times AH \times \dfrac{1}{2}=6 \times 6\sqrt{2} \times \dfrac{1}{2} \)
\( =18\sqrt{2} \; (cm^2) \)
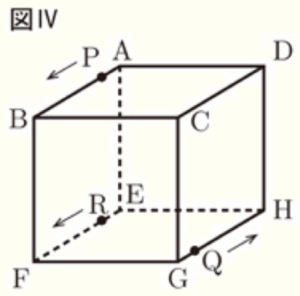
4 図Ⅳは,図Ⅲにおいて,頂点 \( E \) を出発して,頂点 \( F \) まで動く点 \( R \) を示したものである。3点 \( P,Q,R \) は,それぞれ頂点 \( A,G,E \) を同時に出発して,頂点 \( B,H,F \) まで同じ速さで動く。
このとき,\( △PQR \) が動いてできる立体の体積を求めなさい。
【解答】
\( 18 \sqrt{2} \; cm^2 \)
【解説】
問3と同じようにできる立体を考えると,右の図のようになります。
この立体を面 \( O’EF \) で切断すると,
この立体は,四角すい \( O’-ABFE \),三角すい \( O’-OEF \),
三角すい \( O’-OGH \) の3つに分かれます。
【四角すい \( O’-ABFE \) の体積】
線分 \( O’O \) は面 \( EFGH \) に対して垂直なので,
点 \( O \) が対角線の交点にあたることから,
四角すい \( O’-ABFE \) の高さは \( 3 \; cm \) になります。
よって,
四角すい \( O’-ABFE=6 \times 6 \times 3 \times \dfrac{1}{3}=36 \; (cm^3) \)
四角すい \( O’-ABFE \)
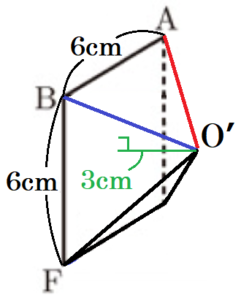
【三角すい \( O’-OGH \) の体積】
\( △BFH \) において,\( FO=HO,BO’=HO’ \) より,
\( BF:O’O=2:1 \) なので,\( O’O=\dfrac{1}{2}BF=3 \; (cm) \)
また,\( △OGH=\dfrac{1}{4} \) 正方形 \( EFGH \) なので,
三角すい \( O’-OGH=6 \times 6 \times \dfrac{1}{4} \times 3 \times \dfrac{1}{3}=9 \; (cm^3) \)
三角すい \( O’-OGH \)
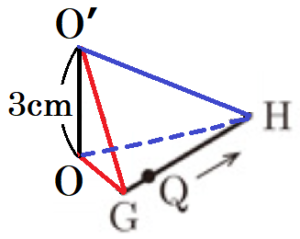
【三角すい \( O’-OEF \) の体積】
\( △OGH=△OEF \),高さ共通より,
三角すい \( O’-OEF \) と三角すい \( O’-OGH \) の体積は等しい。
三角すい \( O’-OEF \)
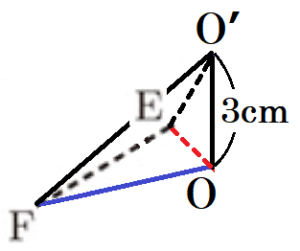
以上より,求める立体の体積は,
四角すい \( O’-ABFE+ \) 三角すい \( O’-OEF+ \) 三角すい \( O’-OGH \)
\( =36+9+9 \)
\( =54 \; (cm^3) \)