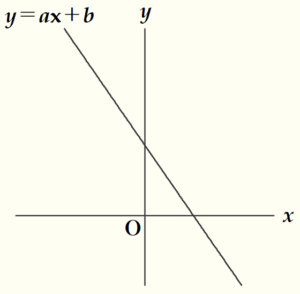大問1
(1) \( -2×(4-7) \) を計算しなさい。
【解説】
\( =-2×(-3) \)
\( =6 \)
(2) \( 5a+2b-2(3a-b) \) を計算しなさい。
【解説】
\( =5a+2b-6a+2b \)
\( =-a+4b \)
(3) ある数 \( x, y \) があり,\( y \) は \( x \) を2倍して \( 3 \) を加えた数より大きい。\( x \) と \( y \) の関係を不等式で表しなさい。
【解説】
\( x \) を2倍して \( 3 \) を加えた数は,\( 2x+3 \) と表すことができるので,
\( y>2x+3 \) となります。
(4) 等式 \( 4a+5b=8 \) を \( a \) について解きなさい。
【解答】
\( a=\dfrac{-5b+8}{4} \) または,\( -\dfrac{5}{4}b+2 \)
【解説】
\( 4a=-5b+8 \)
\( a=\dfrac{-5b+8}{4} \) または,\( a=-\dfrac{5}{4}b+2 \)
(5) \( \sqrt{18}-\dfrac{4}{\sqrt{2}} \) を計算しなさい。
【解説】
\( =3\sqrt{2}-\dfrac{4 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} \)
\( =3\sqrt{2}-2\sqrt{2} \)
\( =\sqrt{2} \)
(6) 連立方程式 \( \left\{ \begin{array}{}
3x+y=5 \\
x-2y=11 \\
\end{array} \right. \) を解きなさい。
【解説】
\( \left\{ \begin{array}{}
3x+y=5 \;\; ・・・ \;\; ➀ \\
x-2y=11 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( \times 2 \) すると,
\( 6x+2y=10 \) ・・・ ➀’
➀’\( + \) ➁ すると,
\( 7x=21 \)
\( x=3 \)
➀ に代入すると,
\( 3 \times 3+y=5 \)
\( 9+y=5 \)
\( y=-4 \)
(7) 方程式 \( 3x^2-x-1=0 \) を解きなさい。
【解答】
\( x=\dfrac{1±\sqrt{13}}{6} \)
【解説】
解の公式より,
\( x=\dfrac{-(-1)±\sqrt{(-1)^2-4 \times 3 \times (-1)}}{2 \times 3} \)
\( =\dfrac{1±\sqrt{1+12}}{6} \)
\( =\dfrac{1±\sqrt{13}}{6} \)
(8) \( x=1+\sqrt{5} \) のとき,\( x^2-2x-3 \) の値を求めなさい。
【解説】
与式を因数分解すると,
\( x^2-2x-3=(x+1)(x-3) \)
\( x=1+\sqrt{5} \) を代入すると,
\( (x+1)(x-3)=(2+\sqrt{5})(-2+\sqrt{5}) \)
\( =(\sqrt{5}+2)(\sqrt{5}-2) \)
\( =5-4 \)
\( =1 \)
(9) 袋の中に,白い碁石だけがたくさん入っている。白い碁石のおよその数を調べるため,この袋の中に黒い碁石を \( 100 \) 個入れ,碁石をよくかき混ぜてから \( 50 \) 個の碁石を無作為に抽出したところ,黒い碁石は \( 7 \) 個含まれていた。袋の中に,白い碁石はおよそ何個入っていたと推定できるか。四捨五入して,十の位まで求めなさい。
【解説】
母集団に含まれる黒い碁石の個数と標本に含まれる黒い碁石の個数の割合(比)は等しいと考えられます。
袋の中の白い碁石の個数を \( x \) 個とすると,
母集団(袋の中)の碁石の数 ・・・ \( x+100 \) 個
母集団に含まれる黒い碁石の個数 ・・・ \( 100 \) 個
標本(取り出した)の碁石の数 ・・・ \( 50 \) 個
標本に含まれる黒い碁石の個数 ・・・ \( 7 \) 個
となるので,
\( x+100:100=50:7 \)
\( 7(x+100)=50 \times 100 \)
\( 7x+700=5000 \)
\( 7x=4300 \)
\( x=614.28・・・ \)
四捨五入して,十の位まで求めるということは,「一の位を四捨五入する」ということなので,
一の位を四捨五入すると,\( x=610 \) となり,
袋の中の白い碁石はおよそ \( 610 \) 個
(10) \( n \) は自然数である。\( \dfrac{n}{12},\dfrac{360}{n} \) がともに整数となる \( n \) は全部で何個あるか,求めなさい。
【解説】
\( \dfrac{n}{12} \) が整数となるのは,\( n \) が \( 12 \) の倍数のとき
\( \dfrac{360}{n} \) が整数となるのは,\( n \) が \( 360 \) の約数のとき
なので,\( \dfrac{n}{12},\dfrac{360}{n} \) がともに整数となるのは,
\( n \) が \( 12 \) の倍数でもあり,\( 360 \) の約数でもあるときです。
\( 360=12 \times 30=12 \times (2 \times 3 \times 5) \) であることから,
\( 12 \) の倍数でもあり,\( 360 \) の約数でもある数 \( n \) を \( n=12 \times m \) と表すとき,
\( m \) は,\( 30 \) の約数になります。
\( 30 \) の約数は \( 1,2,3,5,6,10,15,30 \) なので,
あてはまる \( n \) は,
\( n=12 \times 1=12 \)
\( n=12 \times 2=24 \)
\( n=12 \times 3=36 \)
\( n=12 \times 5=60 \)
\( n=12 \times 6=72 \)
\( n=12 \times 10=120 \)
\( n=12 \times 15=180 \)
\( n=12 \times 30=360 \)
の8個になります。
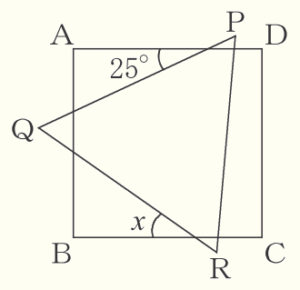
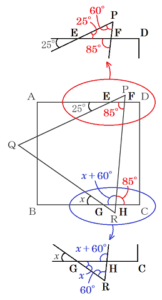
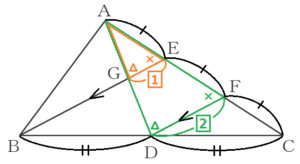
(11) 右の図のように,正方形 \( ABCD \),正三角形 \( PQR \) がある。このとき,\( ∠x \) の大きさを求めなさい。
【解説】
辺 \( AD \) と辺 \( PQ,PR \) の交点をそれぞれ \( E,F \) とすると,
対頂角は等しいので,\( ∠PEF=∠AEQ=25° \),
正三角形 \( PQR \) の内角なので,\( ∠EPF=60° \)
ここから,\( △PEF \) の外角なので,\( ∠EFR=∠PEF+∠EPF=25°+60°=85° \)
正方形の向かい合う辺は平行なので,錯角は等しく,
\( ∠FHC=∠EFR=85° \)
辺 \( BC \) と辺 \( QR,PR \) の交点をそれぞれ \( G,H \) とすると,
対頂角は等しいので,\( ∠RGH=∠BGQ=x \),
正三角形 \( PQR \) の内角なので,\( ∠GRH=60° \)
ここから,\( △RGH \) の外角なので,\( ∠GHF=∠RGH+∠GRH=x+60° \)
3点 \( G,H,C \) は一直線上の点なので,
\( ∠GHF+∠FHC=180° \)
\( (x+60°)+85°=180° \)
\( x=35° \)
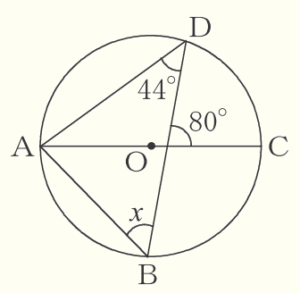
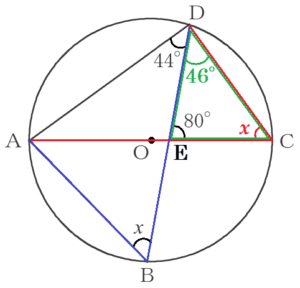
(12) 右の図で,4点 \( A,B,C,D \) は円 \( O \) の周上の点であり,線分 \( AC \) は円 \( O \) の直径である。このとき,\( ∠x \) の大きさを求めなさい。
【解説】
\( \stackrel{\huge\frown}{ AD } \) に対する円周角なので,
\( ∠ACD=∠ABD=x \)
直径 \( AC \) に対する円周角なので,
\( ∠ADC=90° \) ,
線分 \( AC \) と線分 \( BD \) の交点を点 \( E \) とすると,
\( ∠CDE=∠ADC-∠ADE \)
\( =90°-44° \)
\( =46° \)
三角形の内角の和は \( 180° \) なので,
\( ∠ACD=180°-(∠CDE+∠CED) \)
\( =180°-(46°+80°) \)
\( =54° \)
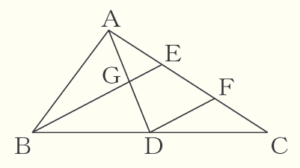
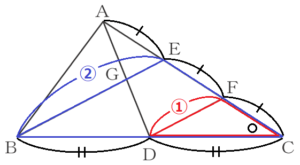
(13) 右の図のように,\( △ABC \) がある。点 \( D \) は辺 \( BC \) の中点であり,点 \( E,F \) は辺 \( AC \) を3等分する点である。点 \( G \) は線分 \( AD \) と線分 \( BE \) の交点である。\( DF=5 \; cm \) のとき,線分 \( BG \) の長さを求めなさい。
【解答】
\( \dfrac{15}{2} \; cm \)
【解説】
\( △CDF \) と \( △CBE \) に注目すると,
\( CD:CB=CF:CE=1:2 \)
\( ∠C \) は共通
なので,
\( △CDF \) ∽ \( △CBE \) で,相似比は \( 1:2 \)
相似な三角形の対応する辺の比は等しいので,
\( DF:BE=1:2 \)
\( 5:BE=1:2 \)
\( BE=10 \; (cm) \)
\( △AGE \) と \( △ADF \) に注目すると,
\( △CDF \) ∽ \( △CBE \) より,
\( DF // BE \) なので,
\( ∠AGE=∠ADF,∠AEG=∠AFD \)
であり,\( △AGE \) ∽ \( △ADF \)
相似な三角形の対応する辺の比は等しいので,
\( GE:DF=AE:AF \)
\( GE:DF=1:2 \)
\( GE:5=1:2 \)
\( GE=\dfrac{5}{2} \; (cm) \)
以上より,
\( BG=BE-GE \)
\( =10-\dfrac{5}{2} \)
\( =\dfrac{15}{2} \; (cm) \)
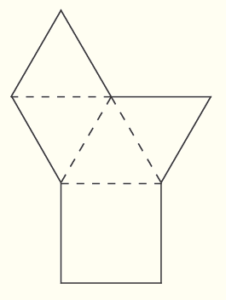
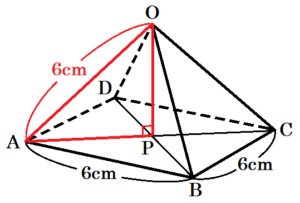
(14) 右の図は,すべての辺の長さが \( 6 \; cm \) の正四角錐の展開図である。この展開図を組み立ててできる正四角錐の体積を求めなさい。
【解答】
\( 36\sqrt{2} \; cm^3 \)
【解説】
組み立てた正四角すいを \( O-ABCD \),底面の正方形 \( ABCD \) における対角線の交点を \( P \)
とすると,\( OP \) がこの正四角すいの高さになります。
このとき,\( △OAP \) に注目すると,
正方形の対角線はそれぞれの中点で交わるので,
\( AP=\dfrac{1}{2}AC \)
\( =\dfrac{1}{2} \times \sqrt{2}AB \)
\( =\dfrac{1}{2} \times \sqrt{2} \times 6 \)
\( =3\sqrt{2} \; (cm) \)
三平方の定理より,
\( OP^2=OA^2-AP^2 \)
\( =6^2-(3\sqrt{2})^2 \)
\( =18 \)
\( OP=3\sqrt{2} \; (cm) \) (\( OP>0 \) より)
よって,この正四角すいの体積は
\( (6 \times 6) \times 3\sqrt{2} \times \dfrac{1}{3}=36\sqrt{2} \; (cm^3) \)
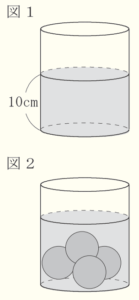
(15) 図1のように, 底面の半径が \( 8 \; cm \), 高さが \( 18 \; cm \) の円柱の形をした容器に,底から \( 10 \; cm \) の高さまで水を入れ, 水平な台の上に置いた。この容器に、図2のように, 半径 \( 3 \; cm \) の球の形をした穴の空いていないガラス玉4個を, 水がこぼれないように入れたところ,水面が上昇した。このとき, 容器の底から水面までの高さを求めなさい。ただし, 容器の厚みは考えないものとする。
【解答】
\( \dfrac{49}{4} \; cm \)
【解説】
ガラス玉4個を入れた後の見かけの水の体積は
見かけの水の体積 \( = \) 水の体積 \( + \) ガラス玉4個の体積
になります。
つまり,水面が上昇した分の体積は,ガラス玉4個の体積と等しくなります。
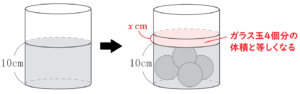
ガラス玉4個を入れたことで上昇した水面の高さを \( x \; cm \) とすると,
水面が上昇した分の体積は,
\( \pi{} \times 8^2 \times x \; (cm^3) \)
ガラス玉4個の体積は,
\( \left(\dfrac{4}{3} \times \pi{} \times 3^3 \right) \times 4 \; (cm^3) \)
なので,
\( \pi{} \times 8^2 \times x=\left(\dfrac{4}{3} \times \pi{} \times 3^3 \right) \times 4 \)
\( 2^2x=3^2 \)
\( x=\dfrac{9}{4} \; (cm) \)
よって,容器の底から水面までの高さは,
\( 10+\dfrac{9}{4}=\dfrac{49}{4} \; (cm) \)
大問2
(1) ある学級でクイズ大会を行った。クイズは全部で \( 20 \) 問出題され,参加者はすべてのクイズに解答した。正解の場合は1問につき \( 10 \) 点加点され,不正解の場合は1問につき \( 5 \) 点減点される。このクイズ大会の優勝者の最終得点は \( 155 \) 点だった。
佳奈さんは,優勝者の正解数を求めるために,正解数を \( x \) 問として方程式をつくった。佳奈さんの[メモ]が正しくなるように, a にあてはまる式を書きなさい。
[メモ]
・正 解 ・・・ 1問につき 「\( +10 \) 点」
・不正解 ・・・ 1間につき 「\( -5 \) 点」
・正解と不正解の数を合わせると \( 20 \) 問
正解数を \( x \) 問とすると,
a \( =155 \)
【解答】
a ・・・ \( 10x-5(20-x) \)
【解説】
全部で \( 20 \) 問出題されたので,不正解だったのは \( 20-x \) 問であり,
\( x \) 問正解して加点された得点は \( 10x \) 点 ・・・ ➀
不正解により減点された得点は \( -5(20-x) \) 点 ・・・ ➁
と表すことができます。
このとき,最終得点(➀,➁)の合計は \( 155 \) 点だったので,
これらの関係を表す方程式は,
\( 10x-5(20-x)=155 \)
(2) 大和さんは,連続する3つの整数にはどのような性質があるか,次のように調べて予想した。大和さんの[予想]がいつでも成り立つことの[説明]が正しくなるように, ア , イ には式を, ウ には説明の続きを書き,完成させなさい。
[調べたこと]
・ \( 1,2,3 \) のとき
\( 1+3=4 \)
\( =2×2 \)
・ \( 2,3,4 \) のとき
\( 2+4=6 \)
\( =3×2 \)
・ \( 3,4,5 \) のとき
\( 3+5=8 \)
\( =4×2 \)
[予想]
最も小さい整数と最も大きい整数の和は,真ん中の整数の2倍になる。
[説明]
\( n \) を整数とすると, 連続する3つの整数は小さいものから順に,\( n \), ア , イ と表すことができる。このとき,最も小さい整数と最も大きい整数の和を,\( n \) を用いて表すと,
ウ
したがって, 最も小さい整数と最も大きい整数の和は, 真ん中の整数の2倍になる。
【解答】
ア ・・・ \( n+1 \)
イ ・・・ \( n+2 \)
ウ
\( n+(n+2)=2n+2 \)
\( =2(n+1) \)
\( n+1 \) は真ん中の整数なので,\( 2(n+1) \) は真ん中の整数の2倍である。
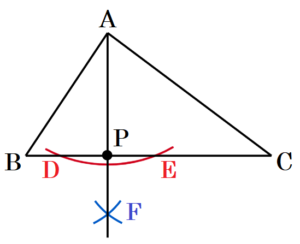
(3) 次の図のように,\( △ABC \) がある。辺 \( BC \) 上に,\( ∠APC=90° \) となる点 \( P \) を,定規とコンパスを用いて作図しなさい。ただし,作図に用いた線は消さないこと。
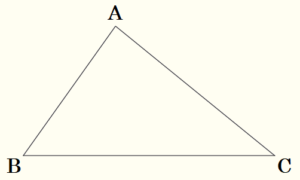
【解答・解説】
\( ∠APC=90° \) ということは,直線 \( AP \) と直線 \( PC \) は垂直に交わるということです。
点 \( P \) は,辺 \( BC \) 上の点なので,直線 \( AP \) と辺 \( BC \) は垂直に交わるともいえます。
つまり,直線 \( AP \) は辺 \( BC \) の垂線になります。
手順1 点 \( A \) を中心に円弧を描く。
(辺 \( BC \) との交点を点 \( D,E \) とします。)
手順2 2点 \( D,E \) を中心に円弧を描く。
(交点を点 \( F \) とします。)
手順3 2点 \( A,F \) を通る直線を描く。
手順3の直線と辺 \( BC \) との交点が求める点 \( P \) になります。
(4) 次の①,②の問いに答えなさい。
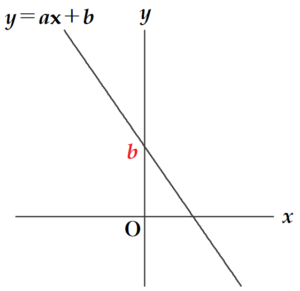
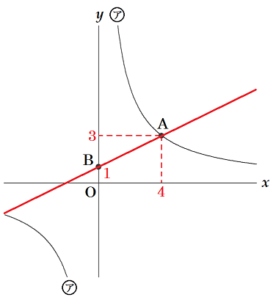
① 右の図のような1次関数 \( y=ax+b \) (\( a,b \) は定数) のグラフが
ある。このときの \( a,b \) について,式の値が必ず正の数となるものを,
次のア~エから1つ選んで記号を書きなさい。
ア \( a+b \) イ \( a-b \) ウ \( b-a \) エ \( ab \)
【解説】
\( y=ax+b \) の直線は右下がりになっているので,
傾き \( a \) は負の値になります。
また,グラフより \( y \) 切片 \( b \) は正の値になっています。
よって,
ア \( a+b \) の値は 負の数 \( + \) 正の数 で求められるので,
\( a \) の絶対値の方が大きいとき,\( a+b \) の値は負の数になります。
イ \( a-b \) の値は 負の数 \( – \) 正の数 で求められるので,\( a-b \) の値は必ず負の数になります。
ウ \( b-a \) の値は 正の数 \( – \) 負の数 で求められるので,\( b-a \) の値は必ず正の数になります。
エ \( ab \) の値は 負の数 \( \times \) 正の数 で求められるので,\( ab \) の値は必ず負の数になります。
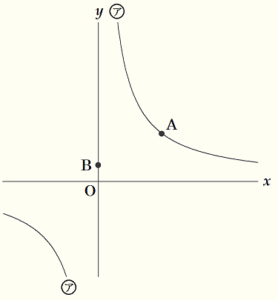
② 右の図において,アは関数 \( y=\dfrac{12}{x} \) のグラフである。点 \( A \) はア上の点で,\( x \) 座標は \( 4 \) である。点 \( B \) は \( y \) 軸上の点で,\( y \) 座標は \( 1 \) である。このとき,2点 \( A,B \) を通る直線の式を求めなさい。
【解答】
\( y=\dfrac{1}{2}x+1 \)
【解説】
点 \( A \) はア上の点で,\( x \) 座標は \( 4 \) なので,
\( y \) 座標は
\( y=\dfrac{12}{4}=3 \)
であり,点 \( A \) の座標は \( A(4,3) \)
点 \( B \) は \( y \) 軸上の点で,
\( y \) 座標は \( 1 \) なので,
点 \( B \) の座標は \( B(0,1) \)
直線 \( AB \) の式を \( y=ax+b \) とすると,
\( a=\dfrac{3-1}{4-0}=\dfrac{1}{2} \)
\( y=\dfrac{1}{2}x+b \) に \( x=0,y=1 \) を代入すると,
\( 1=0+b \)
\( b=1 \)
よって,求める直線の式は \( y=\dfrac{1}{2}x+1 \)
大問3
長方形 \( ABCD \) があり,\( AB<AD \) である。点 \( C \) がこの長方形の周上にくるように1回だけ折り返し,点 \( C \) が移った点を \( P \) とする。次の(1)~(3)の問いに答えなさい。
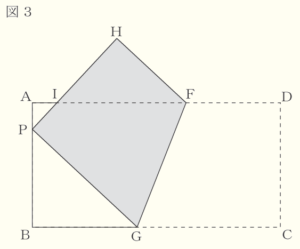
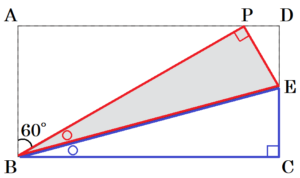
(1) 図1のように,折り目が点 \( B \) を通り,点 \( C \) が辺 \( AD \) 上にくるように折り返す。折り目の直線と辺 \( CD \) の交点を \( E \) とする。\( ∠ABP=60° \) のとき,\( ∠BEP \) の大きさを求めなさい。
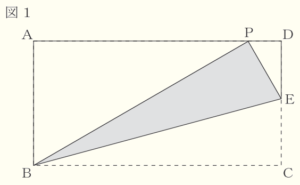
【解説】
長方形の内角は \( 90° \) なので,
\( ∠PBC=∠ABC-∠ABP \)
\( =90°-60° \)
\( =30° \) ・・・ ➀
\( △BPE \) は \( △BCE \) を折り返したものなので,
\( △BPE≡△BCE \)
であり,対応する角は等しいので,
\( ∠PBE=∠CBE \) ・・・ ➁
➀➁より,
\( ∠PBE=\dfrac{1}{2}∠PBC=15° \)
よって,
\( ∠BEP=180°-(∠PBE+∠BPE) \)
\( =180°-(15°+90°) \)
\( =75° \)
(2) 優さんと光さんは,点 \( C \) が辺 \( AB \) 上にくるように折り返す場合について考えた。折り目の直線と辺 \( AD,BC \) との交点をそれぞれ \( F,G \) とし,点 \( D \) が移った点を \( H \) とする。
① 優さんは,図2のように,点 \( C \) が点 \( A \) に重なるように折り返す場合について考えた。[優さんの説明]が正しくなるように, a にはあてはまる角を下のア~ウから1つ選んで記号を, b にはあてはまる言葉を書きなさい。
[優さんの説明]
図2で,\( △ABG \) と \( △AHF \) が合同であることが証明できます。
[証明]
\( △ABG \) と \( △AHF \) において
仮定から,
\( AB=CD=AH \) ・・・ ➀
\( ∠B=∠D=∠H \) ・・・ ➁
また,
\( ∠BAD=∠HAG=90° \) だから,
\( ∠BAG=90°- \) a
\( ∠HAF=90°- \) a
これより,
\( ∠BAG=∠HAF \) ・・・ ➂
➀,➁,➂より,
b から,
\( △ABG≡△AHF \)
ア \( ∠AFG \) イ \( ∠AGF \) ウ \( ∠FAG \)
【解答】
a ・・・ ウ \( ∠FAG \)
b ・・・ 1組の辺とその両端の角がそれぞれ等しい
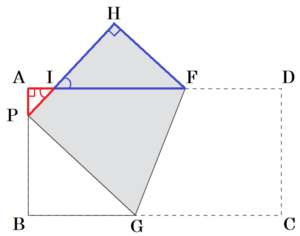
➁ 優さんの説明を聞いた光さんは,図3のように,点 \( C \) が2点 \( A,B \) を除く辺 \( AB \) 上にくるように折り返す場合について考えた。辺 \( AD \) と線分 \( PH \) の交点を \( I \) とする。[光さんの説明]が正しくなるように,[証明]の続きを書き,完成させなさい。
[光さんの説明]
図3で,\( △API \) と \( △HFI \) が相似であることが証明できます。
[証明]
\( △API \) と \( △HFI \) において
\( \phantom{ } \)
\( \phantom{ } \)
\( \phantom{ } \)
\( \phantom{ } \)
【解答】
仮定から,
\( ∠A=∠H \) ・・・ ➀
対頂角は等しいから,
\( ∠AIP=∠HIF \) ・・・ ➁
➀,➁より,2組の角がそれぞれ等しいから,
\( △API \) ∽ \( △HFI \)
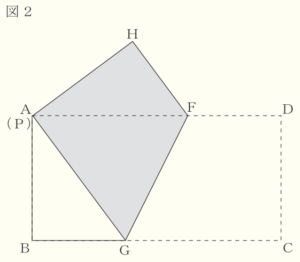
(3) 図4のような \( AB=12 \; cm \) の長方形を,図5のように,点 \( C \) が辺 \( AB \) の中点に重なるように折り返す。折り目の直線と辺 \( AD,BC \) との交点をそれぞれ \( F,G \) とし,点 \( D \) が移った点を \( H \),辺 \( AD \) と線分 \( PH \) の交点を \( I \) とする。\( IH=4 \; cm \) のとき,辺 \( BC \) の長さを求めなさい。
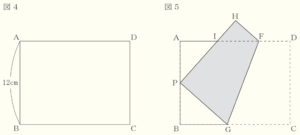
【解答】
\( BC=6\sqrt{7} \; cm \)
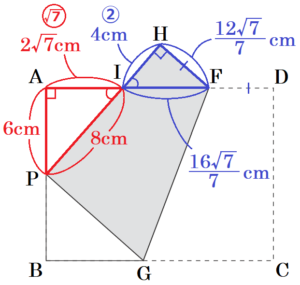
【解説】
(2)➁ より,\( △API \) ∽ \( △HFI \) であることを参考にすると,
\( AD=BC \) より,\( AI,IF,FD \) の長さがわかれば,辺 \( BC \) の長さを求められることになります。
【\( AI \) の長さを求める】
\( HP=DC=AB=12 \; cm \) なので,
\( IH=4 \; cm \) より,\( IP=8 \; (cm) \)
\( △API \) において,三平方の定理より,
\( AI^2=8^2-6^2=28 \)
\( AI=2\sqrt{7} \; (cm) \)
【\( IF \) の長さを求める】
\( △API \) ∽ \( △HFI \) より,
\( IP:IF=AI:HI \)
\( 8:IF=2\sqrt{7}:4 \)
\( IF=\dfrac{16\sqrt{7}}{7} \; (cm) \)
【\( FD \) の長さを求める】
\( △API \) ∽ \( △HFI \) より,
\( PA:FH=AI:HI \)
\( 6:FH=2\sqrt{7}:4 \)
\( FH=\dfrac{12\sqrt{7}}{7} \; (cm) \)
折り返す前後の同じ線分なので,
\( FD=FH=\dfrac{12\sqrt{7}}{7} \; cm \)
以上より,
\( BC=AD=AI+IF+FD \)
\( =2\sqrt{7}+\dfrac{16\sqrt{7}}{7}+\dfrac{12\sqrt{7}}{7} \)
\( =6\sqrt{7} \; (cm) \)
\( \phantom{ } \)
大問4
(1) 次の図のように,数直線上の \( 0 \) の位置に点 \( P \) がある。\( 1 \) から \( 6 \) までの目が出るさいころを2回投げて,1回目に出た目を \( a \),2回目に出た目を \( b \) とする。点 \( P \) は数直線上を正の方向に \( a \) だけ動いた後,負の方向に \( b \) だけ動いて止まる。
このとき,絶対値が \( 1 \) 以下の範囲に,点 \( P \) が止まる確率を求めなさい。ただし,さいころのどの目が出ることも同様に確からしいものとする。

【解説】
止まる場所の数は \( a-b \) で求めることができます。
\( a-b \) の値の絶対値が \( 1 \) 以下の範囲になるのは \( -1≦a-b≦1 \) のときです。
(\( 1 \)
以下なので,\( -1 \) と \( 1 \) も含みます。)
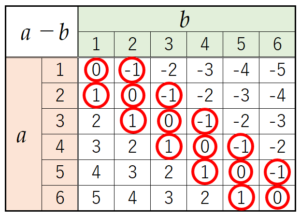
\( a \) と \( b \) の組み合わせとそれぞれの場合における \( a-b \) の値を表に書き出すと,
\( -1≦a-b≦1 \) を満たす組み合わせは \( 16 \) 通り,
全ての組み合わせは \( 36 \) 通りなので,
求める確率は \( \dfrac{16}{36}=\dfrac{4}{9} \)
(2) ある中学校の3年A組と3年B組の生徒全員を対象として,11月に図書館から借りた本の冊数を調べた。次の図は,調べた結果を学級別に分けて,箱ひげ図に表したものである。生徒数は,3年A組が \( 23 \) 人,3年B組が \( 22 \) 人である。
この箱ひげ図から読み取れることとして正しいものを,下のア~オからすべて選んで記号を書きなさい。
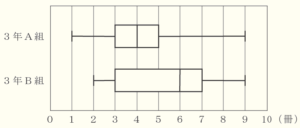
ア 3年A組の中央値は,3年B組の中央値と等しい。
イ 3年A組の最大値は,3年B組の最大値と等しい。
ウ 四分位範囲は,3年B組のほうが3年A組よりも小さい。
エ 借りた本の冊数が \( 3 \) 冊以上 \( 5 \) 冊以下の人数は,3年B組のほうが3年A組よりも多い。
オ 借りた本の冊数が \( 6 \) 冊以上の人数は,3年B組が3年A組の2倍以上である。
【解説】
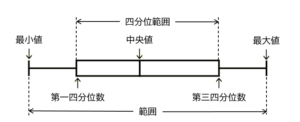
【正しくない理由】
ア ・・・ 3年A組の中央値は \( 4 \) 冊,3年B組の中央値は \( 6 \) 冊なので,等しくありません。
ウ ・・・ 3年A組の四分位範囲は \( 5-3=2 \) 冊,
3年B組の四分位範囲は \( 7-3=4 \) 冊
なので,等しくありません。
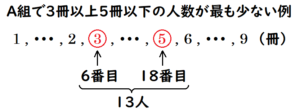
エ ・・・ 3年A組の第一四分位数が \( 3 \) 冊,第三四分位数が \( 5 \) 冊であり,生徒数が \( 23 \) 人なので,
第一四分位数になるのは少ない方から \( 6 \) 番目,
第三四分位数になるのは少ない方から \( 18 \) 番目の冊数であり,
借りた本の冊数が \( 3 \) 冊以上 \( 5 \) 冊以下の人数は,少なくとも \( \color{red}{13} \) 人はいるとわかります。
3年B組の第一四分位数が \( 3 \) 冊,中央値が \( 6 \) 冊であり,生徒数が \( 22 \) 人なので,
中央値になるのは少ない方から \( 11 \) 番目と \( 12 \) 番目の冊数の平均値であり,
借りた本の冊数が \( 3 \) 冊以上 \( 5 \) 冊以下の人数は,多くても \( \color{blue}{10} \) 人とわかります。
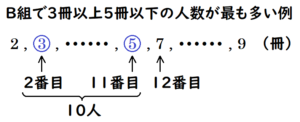
よって,3年A組のほうが3年B組よりも多いことになります。
【正しい理由】
イ ・・・ 最大値は,両組ともに \( 9 \) 冊で等しい。
オ ・・・ 3年A組の第三四分位数が \( 5 \) 冊であり,生徒数が \( 23 \) 人なので,
第三四分位数になるのは多い方から \( 6 \) 番目の冊数であり,
借りた本の冊数が \( 6 \) 冊以上の人数は,多くても \( \color{red}{5} \) 人とわかります。
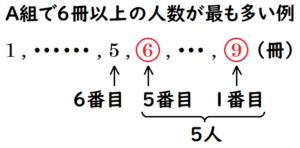
3年B組の中央値が \( 6 \) 冊であり,生徒数が \( 22 \) 人なので,
中央値になるのは多い方から \( 11 \) 番目と \( 12 \) 番目の冊数の平均値であり,
借りた本の冊数が \( 6 \) 冊以上の人数は,少なくとも \( \color{blue}{11} \) 人はいるとわかります。
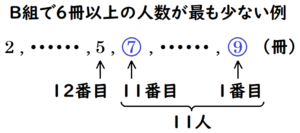
よって,3年B組が3年A組の2倍以上になっています。
大問5
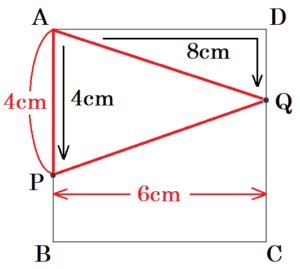
Ⅰ 次の図のように,1辺の長さが \( 6 \; cm \) の正方形 \( ABCD \) がある。2点 \( P,Q \) は《ルール》にしたがって動く。
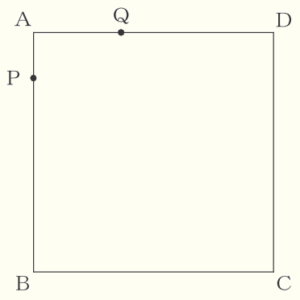
《ルール》
2点 \( P,Q \) は点 \( A \) を同時に出発する。点 \( P \) は毎秒 \( 1 \; cm \) の速さで,辺 \( AB \) 上を \( A→B→A \) の順に動き,点 \( A \) で止まる。点 \( Q \) は毎秒 \( 2 \; cm \) の速さで,辺 \( AD,DC \) 上を \( A→D→C \) の順に動き,点 \( C \) で止まる。
2点 \( P,Q \) が点 \( A \) を出発してから \( x \) 秒後の \( △APQ \) の面積を \( y \; cm^2 \) とする。ただし,点 \( P \) が点 \( A \) にあるときは \( y=0 \) とする。次の(1)~(3)の問いに答えなさい。
(1) \( x=4 \) のとき,\( y \) の値を求めなさい。
【解説】
\( x=4 \) のとき,
点 \( P \) は,点 \( A \) から \( 4 \; cm \),
点 \( Q \) は,点 \( A \) から \( 8 \; cm \)
移動していて,
右の図の位置に2点 \( P,Q \) はあるので,
\( y=4 \times 6 \times \dfrac{1}{2}=12 \; (cm^2) \)
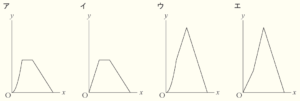
(2) \( x \) と \( y \) の関係を表す最も適切なグラフを,次のア~エから1つ選んで記号を書きなさい。
【解説】
2点 \( P,Q \) が,正方形 \( ABCD \) のどの辺上にあるのかに注目して場合分けをしていきます。
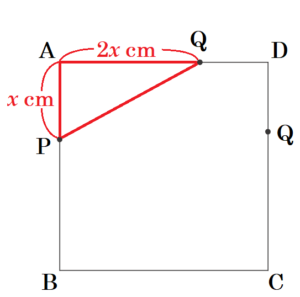
【\( 0≦x≦3 \) の場合】
\( x=3 \) のとき,
点 \( P \) は \( 3 \; cm \),点 \( Q \) は \( 6 \; cm \)
移動しているので,
\( 0≦x≦3 \) のとき,
点 \( P \) は,辺 \( AB \) 上,点 \( Q \) は,辺 \( AD \) 上
にあります。
この範囲のとき,\( y \) を \( x \) の式で表すと,
\( y=x \times 2x \times \dfrac{1}{2}=x^2 \)
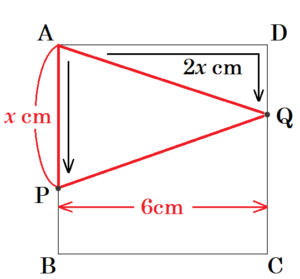
【\( 3≦x≦6 \) の場合】
\( x=6 \) のとき,
点 \( P \) は \( 6 \; cm \),点 \( Q \) は \( 12 \; cm \)
移動しているので,
\( 3≦x≦6 \) のとき,
点 \( P \) は,辺 \( AB \) 上,点 \( Q \) は,辺 \( DC \) 上
にあります。
この範囲のとき,\( y \) を \( x \) の式で表すと,
\( y=x \times 6 \times \dfrac{1}{2}=3x \)
ア~エのうち,\( 0≦x≦3 \) では曲線,\( 3≦x≦6 \) では右上がりの直線になっているのは
ウ になります。
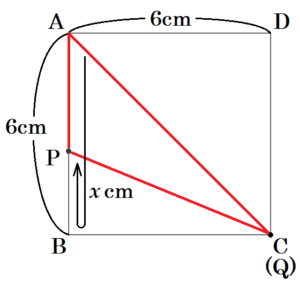
(3) \( 6≦x≦12 \) のとき,\( y=8 \) となる \( x \) の値を求めなさい。求める過程も書きなさい。
【解答】
\( 6≦x≦12 \) における \( △APQ \) の底辺を \( AP \),
高さを \( AD \) とすると,
\( x \) 秒後は,\( AP=12-x \; (cm),AD=6 \; (cm) \) と表すことができるので,
\( y=(12-x) \times 6 \times \dfrac{1}{2} \)
\( =-3x+36 \)
\( y=8 \) を代入すると,
\( 8=-3x+36 \)
\( 3x=28 \)
\( x=\dfrac{28}{3} \)
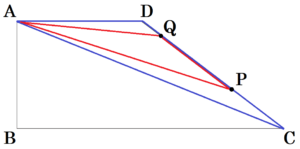
Ⅱ 次の図のように,\( ∠A=∠B=90° \) の台形 \( ABCD \) があり,\( AB=6 \; cm,BC=15 \; cm,DA=7 \; cm \) である。2点 \( P,Q \) は《ルール》にしたがって動く。
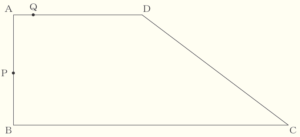
《ルール》
2点 \( P,Q \) は点 \( A \) を同時に出発する。点 \( P \) は毎秒 \( 3 \; cm \) の速さで,台形の辺上を反時計回りに動く。点 \( Q \) は毎秒 \( 1 \; cm \) の速さで,台形の辺上を時計回りに動く。2点 \( P,Q \) は同じ位置になったとき止まる。
2点 \( P,Q \) が点 \( A \) を出発してから \( x \) 秒後の \( △APQ \) の面積を \( y \; cm^2 \) とする。ただし,2点 \( P,Q \) が同じ位置にあるときは \( y=0 \) とする。次の(1)~(3)の問いに答えなさい。
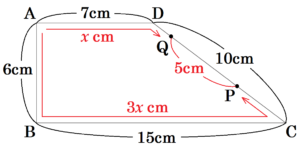
(1) \( 0≦x≦2 \) のとき,\( y=3 \) となる \( x \) の値を求めなさい。
【解説】
\( AB=6 \; cm,DA=7 \; cm \) より,\( 0≦x≦2 \) のとき,
点 \( P \) は辺 \( AB \) 上,点 \( Q \) は辺 \( DA \) 上を移動しています。
\( x \) 秒後の \( AP,AQ \) の長さは,
\( AP=3x \; (cm),AQ=x \; (cm) \) と表せるので,
\( y=3x \times x \times \dfrac{1}{2} \)
\( =\dfrac{3}{2}x^2 \)
\( y=3 \) を代入すると,
\( 3=\dfrac{3}{2}x^2 \)
\( x^2=2 \)
\( x=\sqrt{2} \) (\( 0≦x≦2 \) より)
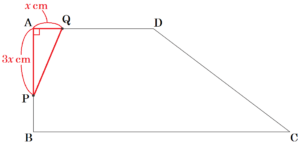
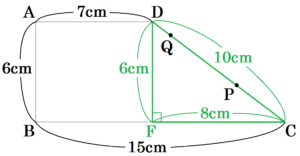
(2) 点 \( P \) が辺 \( BC \) 上にあり,\( PQ=8 \; cm \) となるとき,\( x \) の値を求めなさい。求める過程も書きなさい。
【解答】
点 \( P \) が辺 \( BC \) 上にあるのは,\( 2≦x≦7 \) のときであり,
点 \( Q \) から辺 \( BC \) に垂線をひいた交点を \( E \) とすると,
\( PE=(2x-6) \; cm,QE=6 \; cm \) と表せるので,三平方の定理より,
\( (2x-6)^2+6^2=8^2 \)
\( (x-3)^2=7 \)
\( x-3=±\sqrt{7} \)
\( x=3+\sqrt{7} \) (\( 2≦x≦7 \) より)
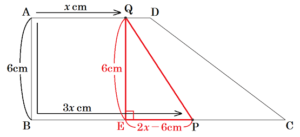
(3) 2点 \( P,Q \) が辺 \( CD \) 上にあり,\( y \) の値が \( △ACD \) の面積の半分になるとき,\( x \) の値を求めなさい。
【解答】
\( x=\dfrac{33}{4} \)
【解説】
\( △ACD \) の底辺を \( CD \),\( △APQ \) の底辺を \( PQ \)
と考えると,高さは共通なので,
\( y \) の値,つまり,\( △APQ \) の面積が
\( △ACD \) の面積の半分になるとき,
\( PQ \) の長さは辺 \( CD \) の長さの半分になります。
点 \( D \) から辺 \( BC \) に垂線をひいた交点を
\( F \) とすると,\( DF=6 \; cm,FC=8 \; cm \) なので,
三平方の定理より,
\( CD^2=6^2+8^2=100 \)
\( CD=10 \; (cm) \) (\( CD>0 \) より)
\( y \) の値が \( △ACD \) の面積の半分になるとき,
\( PQ=5 \; cm \) なので,
\( 3x+x+5=6+7+15+10 \)
\( 4x=33 \)
\( x=\dfrac{33}{4} \)