大問1
1 \( 3-(-4) \)
2 \( 4(x-2y)+3(x+3y-1) \)
【解説】
\( =4x-8y+3x+9y-3 \)
\( =7x+y-3 \)
3 \( \dfrac{15}{8}x^2y \div \left( -\dfrac{5}{6}x \right) \)
【解答】
\( -\dfrac{9}{4}xy \)
【解説】
\( =\dfrac{15}{8}x^2y \times \left( -\dfrac{6}{5x} \right) \)
\( =-\dfrac{15x^2y \times 6}{8 \times 5x} \)
\( =-\dfrac{9}{4}xy \)
4 \( (\sqrt{6}-2)(\sqrt{6}+3)-\dfrac{4\sqrt{3}}{\sqrt{2}} \)
【解説】
\( =(6+\sqrt{6}-6)-\dfrac{4\sqrt{3} \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} \)
\( =\sqrt{6}-2\sqrt{6} \)
\( =-\sqrt{6} \)
5 \( (3x+1)(x-4)-(x-3)^2 \)
【解説】
\( =(3x^2-11x-4)-(x^2-6x+9) \)
\( =2x^2-5x-13 \)
大問2
1 \( 4x^2-9y^2 \) を因数分解せよ。
【解答】
\( (2x+3y)(2x-3y) \)
2 三角すいの底面積を \( S \),高さを \( h \),体積を \( V \) とすると,\( V=\dfrac{1}{3}Sh \) と表される。この等式を \( h \) について解け。
【解答】
\( h=\dfrac{3V}{S} \)
3 次のア~エのうち、正しいものを1つ選び、その記号を書け。
ア \( 3 \) の絶対値は \( -3 \) である。
イ \( m,n \) が自然数のとき,\( m-n \) の値はいつも自然数である。
ウ \( \sqrt{25}=±5 \) である。
エ \( \dfrac{4}{3} \) は有理数である。
【解説】
ア ・・・ ある数の符号をはずしたものが絶対値なので,\( 3 \) の絶対値は \( 3 \) です。
イ ・・・ \( m<n \) のとき,\( m-n \) は負の数になります。負の数は自然数には含まれません。
例: \( m=1,n=3 \) のとき,\( m-n=-2 \)
ウ ・・・ \( \sqrt{25} \) は,\( 25 \) の平方根(\( 2 \) 乗すると \( 25 \) になる数)のうち正の数を表しています。
エ ・・・ 分数の形で表すことができる数が有理数,表せないものが無理数なので,
\( \dfrac{4}{3} \) は有理数になります。
4 2つのさいころを同時に投げるとき,出る目の数の和が5の倍数となる確率を求めよ。ただし,さいころは,1から6までのどの目が出ることも同様に確からしいものとする。
【解説】
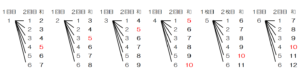
2つのさいころの出る目の組み合わせを樹形図に表すと次のようになります。
和が5の倍数(5,10)になる組み合わせは7通り,すべての場合の数は36通りなので,
求める確率は,\( \dfrac{7}{36} \)
5 下の図のような, 相似比が \( 2:5 \) の相似な2つの容器A,Bがある。 何も入っていない容器Bに,容器Aを使って水を入れる。このとき,容器Bを満水にするには,少なくとも容器Aで何回水を入れればよいか,整数で答えよ。
【解説】
相似な立体の体積比は,相似比の3乗の比になるので,
相似比が \( 2:5 \) の相似な2つの容器の体積比は,\( 2^3:5^3=8:125 \) になります。
よって,\( \dfrac{125}{8}=15+\dfrac{5}{8} \) より,16回水を入れればよいことになります。
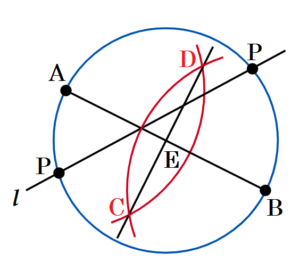
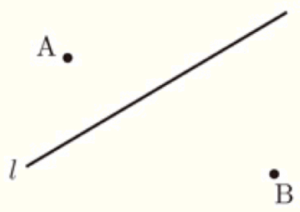
6 下の図のように, 2点 \( A,B \) と直線 \( l \) がある。直線 \( l \) 上にあって,\( ∠APB=90° \) となる点 \( P \) を1つ,解答欄に作図せよ。ただし,作図に用いた線は消さずに残しておくこと。
【解答】
直径に対する円周角は \( 90° \) なので,線分 \( AB \) を直径とする円と直線 \( l \) の交点が求める点 \( P \) になります。
手順1 線分 \( AB \) を描く
手順2 2点 \( A,B \) を中心に円弧を描く
(交点を点 \( C,D \) とします)
手順3 直線 \( CD \) を描く
(線分 \( AB \) との交点を点 \( E \) とします)
手順4 点 \( E \) を中心に円弧を描く
手順4の円弧と直線 \( l \) の交点が求める点 \( P \) になります。
線分 \( AB \) の上下に2か所できます。
どちらを書いても大丈夫です。
7 連続する3つの自然数がある。最も小さい自然数の2乗と中央の自然数の2乗の和が,最も大きい自然数の10倍より5大きくなった。この連続する3つの自然数を求めよ。ただし,用いる文字が何を表すかを最初に書いてから方程式をつくり,答えを求める過程も書くこと。
【解答】
連続する3つの自然数のうち,中央の自然数を \( n \) とすると,
\( (n-1)^2+n^2=10(n+1)+5 \)
\( 2n^2-2n+1=10n+15 \)
\( 2n^2-12n-14=0 \)
\( n^2-6n-7=0 \)
\( (n+1)(n-7)=0 \)
\( n=-1,7 \)
\( n \) は自然数なので,あてはまるのは \( n=7 \)
よって,連続する3つの自然数は,\( 6,7,8 \)
大問3
1 ある中学校の1組,2組,3組で数学のテストを行った。
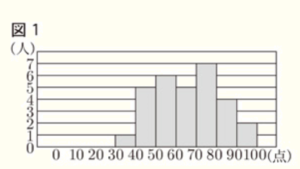
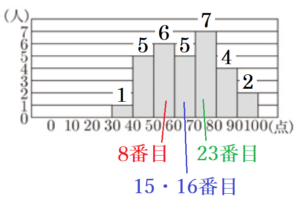
(1) 下の図1は,1組30人の結果をヒストグラムに表したものである。このヒストグラムでは,例えば,40点以上50点未満の生徒が5人いることがわかる。また,下のア~エの箱ひげ図には,1組30人の結果を表したものが1つ含まれている。ア~エのうち,1組30人の結果を表した箱ひげ図として,最も適当なものを1つ選び,その記号を書け。
【解説】
データの総数が30個なので,得点の少ない方から順番に並べたとき,
第一四分位数は8番目の人の得点,第二四分位数は15番目と16番目の人の得点の平均値,
第三四分位数は23番目の人の得点になります。
ヒストグラムから,
最小値が含まれる範囲は30点以上40点未満,
第一四分位数が含まれるのは50点以上60点未満,
第二四分位数が含まれるのは60点以上70点未満,
第三四分位数が含まれるのは70点以上80点未満,
最大値が含まれるのは90点以上100点未満
なので,これらがすべてあてはまるのは イ になります。
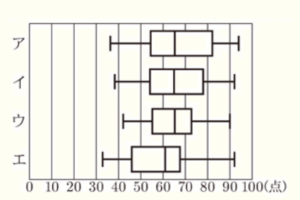
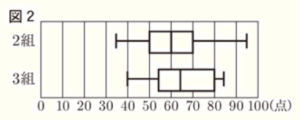
(2) 右の図2は,2組と3組それぞれ30人の結果を箱ひげ図に表したものである。この箱ひげ図から読みとれることとして,下の➀,➁は,「ア 正しい」,「イ 正しくない」,「ウ この箱ひげ図からはわからない」のどれか。ア〜ウのうち,最も適当なものをそれぞれ1つ選び,その記号を書け。
➀ 四分位範囲は,3組より2組の方が大きい。
➁ 点数が45点以下の生徒は,3組より2組の方が多い。
【解説】
➀ 四分位範囲は,箱ひげ図の箱の長さになります。
2組の四分位範囲は \( 70-50=20 \)(点)であるのに対して,2組の四分位範囲は \( 20 \) 点より大きいので,四分位範囲は3組の方が大きい。
➁ 2組の第一四分位数は50点,3組の第一四分位数は約55点なので,45点以下の生徒はともに7人以下であることはわかりますが,その内訳は箱ひげ図だけでは判断できません。
2 太郎さんは,午前9時ちょうどに学校を出発して,図書館に向かった。学校から図書館までは一本道であり,その途中に公園がある。学校から公園までの \( 1200 \; m \) の道のりは分速 \( 80 \; m \) の一定の速さで歩き,公園で10分間休憩した後,公園から図書館までの \( 1800 \; m \) の道のりは分速 \( 60 \; m \) の一定の速さで歩いた。
(1) 太郎さんが公園に到着したのは午前何時何分か求めよ。
【解説】
学校から公園まで進むのにかかる時間は \( \dfrac{1200}{80}=15 \)(分)
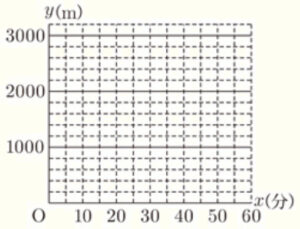
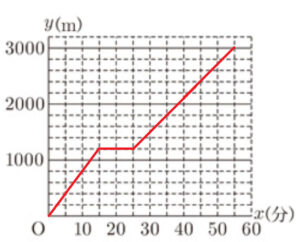
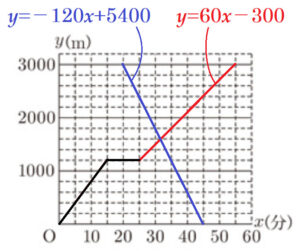
(2) 太郎さんが学校を出発してから \( x \) 分後の学校からの道のりを \( y \; m \) とするとき, 太郎さんが学校を出発してから図書館に到着するまでの \( x \) と \( y \) の関係を表すグラフをかけ。
(3) 花子さんは,午前9時20分ちょうどに図書館を出発し,一定の速さで走って学校へ向かった。途中で太郎さんと出会い,午前9時45分ちょうどに学校に到着した。 花子さんが太郎さんと出会ったのは午前何時何分何秒か求めよ。
【解説】
(2) のグラフに花子さんが走った状態を表す直線を追加します。
この直線の傾きは,\( \dfrac{0-3000}{45-20}=-120 \)
この直線の式を \( y=-120x+b \) とすると,
\( (20,3000) \) を通るので,
\( 3000=-120 \times 20+b \)
\( b=5400 \)
よって,この直線の式は,\( y=-120x+5400 \)
グラフより,花子さんが太郎さんと出会ったのは公園と図書館の間なので,
太郎さんが公園から図書館まで歩いた直線の式を求めます。
歩いた速さが傾きになるので,
この直線の式を \( y=60x+c \) とすると,
\( (25,1200) \) を通るので,
\( 1200=60 \times 25+c \)
\( c=-300 \)
よって,この直線の式は,\( y=60x-300 \)
この2本の直線の式を連立方程式として解くと,
\( x=\dfrac{95}{3},y=1600 \)
\( \dfrac{95}{3}=31+\dfrac{2}{3} \)(分)で,\( \dfrac{2}{3} \)分 \( =60 \times \dfrac{2}{3}=40 \) 秒なので,
2人が出会ったのは,9時31分40秒になります。
大問4
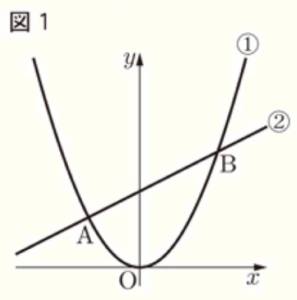
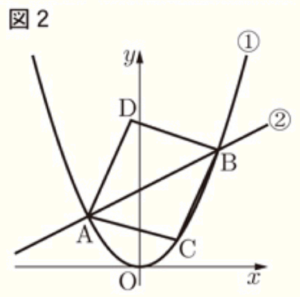
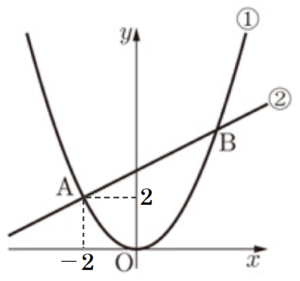
右の図1において, 放物線 ➀ は関数 \( y=ax^2 \) のグラフであり、直線 ➁ は関数 \( y=\dfrac{1}{2}x+3 \) のグラフである。 放物線 ➀ と直線 ➁ は,2点 \( A,B \) で交わっており,\( x \) 座標はそれぞれ \( -2,3 \) である。
このとき,次の問いに答えなさい。
1 関数 \( y=\dfrac{1}{2}x+3 \) について,\( x \) の変域が \( -2≦x≦3 \) のときの \( y \) の変域を求めよ。
【解答】
\( 2≦y≦\dfrac{9}{2} \)
【解説】
\( x=-2 \) のとき,\( y=2 \),\( x=3 \) のとき,\( y=\dfrac{9}{2} \) なので,
\( y \) の変域は,\( 2≦y≦\dfrac{9}{2} \)
2 \( a \) の値を求めよ。
【解答】
\( a=\dfrac{1}{2} \)
【解説】
放物線 ➀ は点 \( A(-2,2) \) を通るので,
\( 2=a \times (-2)^2 \)
\( 4a=2 \)
\( a=\dfrac{1}{2} \)
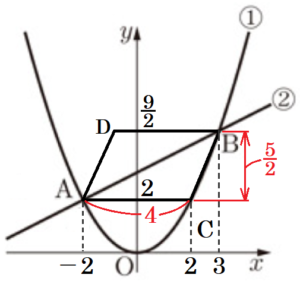
3 下の図2のように, 放物線 ➀ 上に,\( x \) 座標が \( -2 \) より大きく \( 3 \) より小さい点 \( C \) をとり,線分 \( AC,BC \) を隣り合う2辺とする平行四辺形 \( ACBD \) をつくる。
(1) 直線 \( AC \) が \( x \) 軸と平行になるとき, 平行四辺形 \( ACBD \) の面積を求めよ。
【解説】
直線 \( AC \) が \( x \) 軸と平行なので,点 \( C \) の \( y \) 座標は \( 2 \) であり,
\( 2=\dfrac{1}{2}x^2 \)
\( x^2=4 \)
\( x=±2 \)
\( x=-2 \) は点 \( A \) になるので,あてはまるのは \( x=2 \)
よって,\( AC=2-(-2)=4 \)
問1より,点 \( B \) の \( y \) 座標は \( \dfrac{9}{2} \),点 \( C \) の \( y \) 座標は \( 2 \) なので,
平行四辺形 \( ACBD \) の高さは,\( \dfrac{9}{2}-2=\dfrac{5}{2} \)
以上より,平行四辺形 \( ACBD \) の面積は,\( 4 \times \dfrac{5}{2}=10 \)
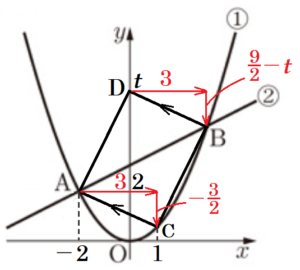
(2) 点 \( D \) が \( y \) 軸上にあるとき,点 \( D \) の \( y \) 座標を求めよ。
【解説】
平行四辺形の向かい合う辺は平行で長さが等しいので,\( AC//BD \) になっています。
このとき,
・ 点 \( A \) から点 \( C \) までの \( x \) の増加量と点 \( D \) から点 \( B \) までの \( x \) の増加量
・ 点 \( A \) から点 \( C \) までの \( y \) の増加量と点 \( D \) から点 \( B \) までの \( y \) の増加量
はどちらも等しくなります。
点 \( D \) から点 \( B \) までの \( x \) の増加量が \( 3 \) なので,
点 \( A \) から点 \( C \) までの \( x \) の増加量も \( 3 \) になります。
このとき,点 \( C \) の \( x \) 座標が \( -2+3=1 \) になることから,
点 \( C \) の \( y \) 座標は,\( y=\dfrac{1}{2} \times 1^2=\dfrac{1}{2} \)
であり,点 \( A \) から点 \( C \) までの \( y \) の増加量は \( \dfrac{1}{2}-2=-\dfrac{3}{2} \)
点 \( D \) の \( y \) 座標を \( t \) とすると,
点 \( D \) から点 \( B \) までの \( y \) の増加量は \( \dfrac{9}{2}-t \) と表せるので,
\( \dfrac{9}{2}-t=-\dfrac{3}{2} \)
\( t=6 \)
大問5
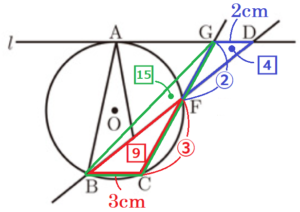
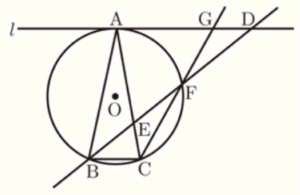
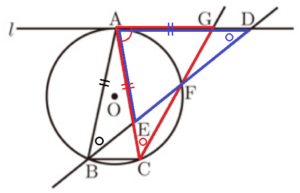
下の図のように,3点 \( A,B,C \) が円 \( O \) の周上にあり, \( AB=AC \) である。点 \( A \) を通り線分 \( BC \) に平行な直線を \( l \) とし,直線 \( l \) 上に点 \( D \) を \( AB=AD \) となるようにとる。直線 \( BD \) と線分 \( AC \) との交点を \( E \) ,直線 \( BD \) と円 \( O \) との交点のうち,点 \( B \) と異なる点を \( F \) とする。また,直線 \( CF \) と直線 \( l \) との交点を \( G \) とする。ただし, \( ∠CAD \) は鋭角とする。
このとき,次の問いに答えなさい。
1 \( △ACG≡△ADE \) であることを証明せよ。
【解答】
\( △ACG \) と \( △ADE \) において,
仮定より,\( AB=AC,AB=AD \) なので,
\( AC=AD \) ・・・ ➀
\( ∠A \) は共通 ・・・ ➁
\( △ABD \) は \( AB=AD \) の二等辺三角形なので,
\( ∠ABF=∠ADE \) ・・・ ➂
弧 \( AF \) の円周角なので,
\( ∠ABF=∠ACF \) ・・・ ➃
➂➃より,\( ∠ACF=∠ADE \) ・・・ ➄
➀➁➄より,
1組の辺とその両端の角がそれぞれ等しいので,
\( △ACG≡△ADE \)
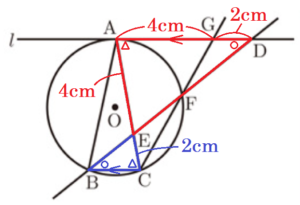
2 \( AG=4 \; cm,GD=2 \; cm \) のとき,
(1) 線分 \( BC \) の長さを求めよ。
【解説】
問1より,\( △ACG≡△ADE \) なので,
\( AC=AD=6 \; cm,AE=AG=4 \; cm, \)
\( EC=AC-AE=2 \; cm \)
仮定より,直線 \( l \; // \) 線分 \( BC \) なので,
\( ∠ADE=∠CBE,∠DAE=∠BCE \)
2組の角がそれぞれ等しいので,
\( △ADE \) ∽ \( △CBE \)
対応する辺の長さは等しいので,
\( AE:CE=AD:BC \)
\( 4:2=6:BC \)
\( BC=3 \; (cm) \)
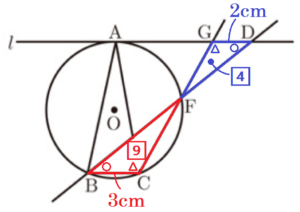
(2) \( △DGF \) の面積を求めよ。
【解答】
\( \dfrac{3\sqrt{15}}{5} \; cm^2 \)
【解説】
\( △CBF \) と \( △DGF \) において,
直線 \( l \; // \) 線分 \( BC \),\( BC=3 \; cm,GD=2 \; cm \) より,
\( △CBF \) ∽ \( △DGF \) で,相似比は \( 3:2 \)
よって,面積比は,
\( △CBF:△DGF=3^2:2^2=9:4 \)
\( △CBF=\dfrac{9}{4}△DGF \)
 直線 \( l \; // \) 線分 \( BC \) なので,
直線 \( l \; // \) 線分 \( BC \) なので,
\( ∠CBF=∠GDF,∠BCF=∠DGF \)
2組の角がそれぞれ等しいので,
\( △CBF \) ∽ \( △DGF \)
補助線 \( BG \) を引くと,\( △CBF \) と \( △CBG \) は底辺の比が \( CF:CG=3:5 \) で高さが共通なので,
\( △CBF:△CBG=3:5 \)
\( △CBG=\dfrac{5}{3}△CBF \)
\( =\dfrac{5}{3} \times \dfrac{9}{4}△DGF \)
\( =\dfrac{15}{4}△DGF \) ・・・ ➀
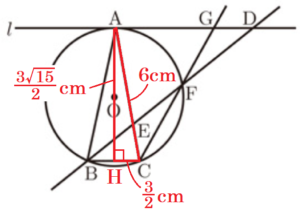
点 \( A \) から線分 \( BC \) に垂線をひき,交点を \( H \) とすると,\( △ABC \) は \( AB=AC=6 \; cm \),
\( BC=3 \; cm \) の二等辺三角形なので,
\( CH=\dfrac{1}{2}BC=\dfrac{3}{2} \; (cm) \)
三平方の定理より,
\( AH^2=AC^2-CH^2 \)
\( =36-\dfrac{9}{4} \)
\( =\dfrac{135}{4} \)
\( AH=\dfrac{3\sqrt{15}}{2} \; (cm) \) (\( AH>0 \) より)
線分 \( AH \) は,\( △CBG \) の高さにあたるので,
\( △CBG=3 \times \dfrac{3\sqrt{15}}{2} \times \dfrac{1}{2}=\dfrac{9\sqrt{15}}{4} \; (cm^2) \) ・・・ ➁
➀➁より,
\( \dfrac{15}{4}△DGF=\dfrac{9\sqrt{15}}{4} \)
\( △DGF=\dfrac{3\sqrt{15}}{5} \; (cm^2) \)





 直線 \( l \; // \) 線分 \( BC \) なので,
直線 \( l \; // \) 線分 \( BC \) なので,