大問1
(1) \( -3+8 \)
(2) \( \left(-\dfrac{9}{2} \right) \div \left(-\dfrac{3}{4} \right) \)
【解説】
\( =\left(-\dfrac{9}{2} \right) \times \left(-\dfrac{4}{3} \right) \)
\( =6 \)
(3) \( (-3a)^2 \times 2a \)
【解説】
\( =9a^2 \times 2a \)
\( =18a^3 \)
(4) \( (\sqrt{3}+1)^2-\dfrac{9}{\sqrt{3}} \)
【解説】
\( =3+2\sqrt{3}+1-3\sqrt{3} \)
\( =4-\sqrt{3} \)
(5) \( (x+4)(x-4)+(x-5)(x-1) \)
【解説】
\( =x^2-16+x^2-6x+5 \)
\( =2x^2-6x-11 \)
大問2
(1) \( x^2-3x-18 \) を因数分解せよ。
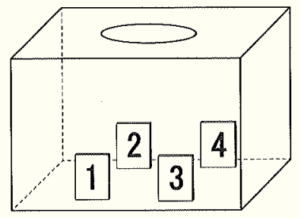
(2) 右の図のように,箱の中に,\( 1,2,3,4 \) の数字が1つずつ書かれた4枚のカードが入っている。この箱の中からカードを1枚取り出し,書かれた数字を見て箱にもどす。このことをくり返し行うときの,カードの出方について述べた文として正しいものを,次のア~エから1つ選び,その記号を書け。ただし,どのカードが取り出されることも同様に確からしいものとする。
ア カードを4000回取り出したとき,\( 1 \) の数字が書かれたカードは1000回ぐらい出る。
イ カードを40回取り出したとき,\( 1 \) の数字が書かれたカードは必ず10回出る。
ウ カードを3回取り出したとき,\( 1 \) の数字が書かれたカードが1回も出なければ,
次は必ず \( 1 \) の数字が書かれたカードが出る。
エ 同じ数字が書かれたカードが2回続けて出ることはない。
【解説】
イ・ウ \( 1 \) の数字が書かれたカードが1回も出ない可能性もあるので,あてはまりません。
エ 箱の中には,常に\( 1,2,3,4 \) の4枚カードが入っているので,
前の結果によって,出るカードが決定されることはありません。
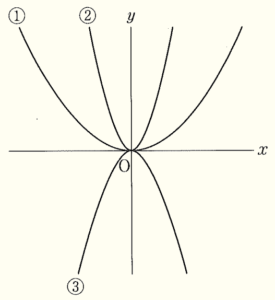
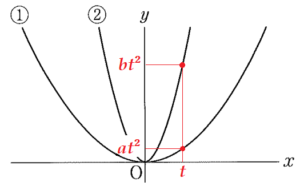
(3) 右の図において,放物線 ①,②,③ はそれぞれ関数 \( y=ax^2,y=bx^2,y=cx^2 \) のグラフである。\( a,b,c \) を,値の小さい順に左から並べて書け。
【解説】
①,② のグラフの形は下に凸,③ のグラフの形は上に凸なので,\( a>0,b>0,c<0 \) であり,
\( c \) の値が一番小さいとわかります。
①,② のグラフにおいて,
\( x=t \) (\( t \) は \( 0 \) 以外の数)とすると,
\( at^2<bt^2 \) となるので,
両辺を \( t^2 \) で割ると,\( a<b \)
よって,\( c<a<b \)
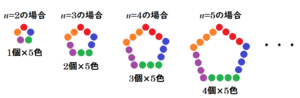
(4) 右の図は,1辺に4個の碁石を並べた正五角形で,並べた碁石は全部で15個である。1辺に \( n \) 個の碁石を並べた正五角形をつくったとき,並べた碁石は全部で何個か,\( n \) を使って表せ。ただし,\( n \) は2以上の自然数とする。
【解説】
各辺ごとに色分けし,各色の碁石の数が等しくなるように分けると,下の図のようになります。
このとき,並べた碁石の総数は,「\( (n-1) \) 個 \( \times 5 \) 色」と表すことができるので,
\( (n-1) \times 5=5n-5 \) と表すことができます。
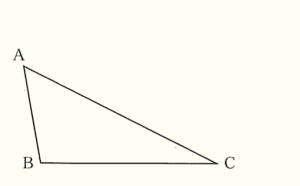
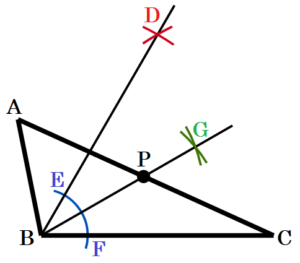
(5) 下の図のような \( △ABC \) がある。辺 \( AC \) 上にあって,\( ∠PBC=30° \) となる点 \( P \) を解答欄に作図せよ。ただし,作図に用いた線は消さずに残しておくこと。
【解答】
手順1 2点 \( B,C \) を中心に辺 \( BC \) を
半径とする円弧を描く。
(交点を点 \( D \) とします。)
手順2 2点 \( B,D \) を通る直線を描く。
手順3 点 \( B \) を中心に円弧を描く。
(辺 \( AB \),直線 \( BD \) との交点を
点 \( E,F \) とします。)
手順4 2点 \( E,F \) を中心に円弧を描く。
(交点を点 \( G \) とします。)
手順5 2点 \( B,G \) を通る直線を描く。
手順5の直線と辺 \( AC \) の交点が求める点 \( P \) になります。
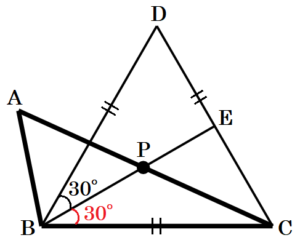
【解説】
\( 30° \) が \( 60° \) の半分であることに注目します。
辺 \( BC \) を1辺とする正三角形 \( BCD \) を描き,
\( ∠DBC \) の二等分線と辺 \( CD \) の交点を
点 \( E \) とすると,
線分 \( BE \) と辺 \( AC \) の交点が求める点 \( P \) になります。
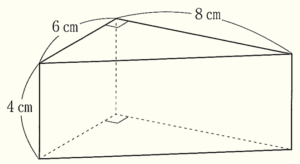
(6) 下の図のような,底面が直角三角形で,側面が全て長方形の三角柱がある。この三角柱の表面積を求めよ。
【解説】
底面の直角三角形の斜辺の長さは,三平方の定理より \( 10 \; cm \) なので,
展開図は下の図のようになります。
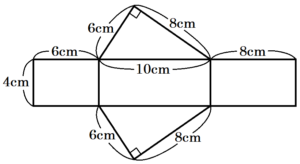
底面の直角三角形1つの面積 \( =6 \times 8 \times \dfrac{1}{2}=24 \; (cm^2) \)
側面の長方形3つ合計の面積 \( =4 \times (6+10+8)=96 \; (cm^2) \)
なので,
三角柱の表面積 \( =24 \times 2+96=144 \; (cm^2) \)
(7) ある市のテニス大会は,下のような要項により開催される。今回,\( 73 \) 人から参加申し込みがあったので,予選リーグの各組の人数は,\( 4 \) 人または \( 5 \) 人になった。\( 4 \) 人の組と \( 5 \) 人の組は,それぞれ何組あるか求めよ。ただし,用いる文字が何を表すかを最初に書いてから連立方程式をつくり,答えを求める過程も書くこと。

【解答】
\( 4 \) 人の組が \( x \) 組,\( 5 \) 人の組が \( y \) 組あるして,
参加する人数とできる組の関係を連立方程式として解くと,
\( \left\{ \begin{array}{}
4x+5y=73 \;\; ・・・ \;\; ➀ \\
x+y=16 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( – \) ➁ \( \times 4 \)
\( y=9 \)
➁ に代入すると,
\( x+9=16 \)
\( x=7 \)
よって,\( 4 \) 人の組は \( 7 \) 組,\( 5 \) 人の組は \( 9 \) 組
大問3
下の会話文は,花子さんが,総合的な学習の時間に,公園で,身の回りの数学について,太郎さんと話をしたときのものである。
花子さん:すべり台の斜面にボールを転がすとき,ボールが斜面を
転がりはじめてからの時間と,その間に進んだ距離には
関係があることを習ったね。
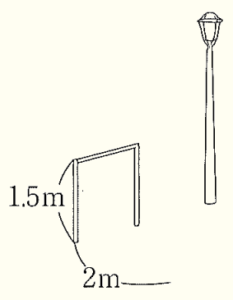
太郎さん:そうだったね。街灯や木の高さを求める方法も習ったよ。
今,高さ \( 1.5 \; m \) の鉄棒の影の長さは \( 2 \; m \),街灯の影の
長さは \( 8 \; m \) だから,街灯の高さは ア \( m \) と分かる
ね。
花子さん:確かにそうなるね。でも,同じ方法で木の高さを求めよう
とすると,木の影の長さは,花壇などの障害物があって
測ることができないね。他に木の高さを求める方法はない
か,先生に質問してみよう。
このとき,次の問いに答えなさい。ただし,地面は水平であり,鉄棒,街灯,木は,地面に対して垂直に立っているものとする。
(1) ある斜面にそって,ボールが転がりはじめてから \( x \) 秒間に進んだ距離を \( y \; m \) とすると,\( y \) は \( x \) の \( 2 \) 乗に比例し,\( x=2 \) のとき \( y=8 \) であった。\( y \) を \( x \) の式で表せ。
【解説】
\( y \) は \( x \) の \( 2 \) 乗に比例するということを式で表すと,
\( y=ax^2 \) と表せるので,\( x=2,y=8 \) を代入すると,
\( 8=a \times 2^2 \)
\( a=2 \)
よって,求める式は,\( y=2x^2 \)
(2) 会話文中の ア に当てはまる数を書け。
【解説】
街灯の高さと街灯の影の長さの比は,鉄棒の高さと鉄棒の影の長さの比と等しくなるので,
街灯の高さを \( a \; m \) とすると,
\( a:8=1.5:2 \)
\( a=6 \; (m) \)
(3) 花子さんの質問に対して,先生は,木の高さを求める方法を次のように説明した。説明文中の イ に当てはまる数を書け。
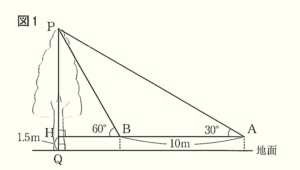
右の
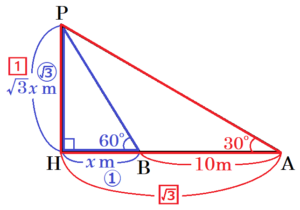
図1のように,木の先端を点 \( P \) とし,点 \( P \) から地面に垂線をひき,地面との交点を \( Q \) とします。花子さんが点 \( P \) を見上げる角度が水平の方向に対して \( 30° \) になるときの花子さんの目の位置を点 \( A \),その場所からまっすぐ木に近づいていき,点 \( P \) を見上げる角度が \( 60° \) になるときの花子さんの目の位置を点 \( B \) とします。また,直線 \( AB \) と線分 \( PQ \) との交点を \( H \) とすると, \( ∠PHA=90° \) です。例えば \( AB=10 \; m \) のとき,\( PH \) の長さは
イ \( m \) となります。花子さんの目の位置の地面からの高さは \( 1.5 \; m \) なので,木の高さ \( PQ \) は \( ( \)
イ \( +1.5) \; m \) となります。
【解説】
\( △PBH \) と \( △APH \) は,
\( 30°,60°,90° \) の直角三角形であることから,
\( BH=x \; m \) とすると,
\( PH=\sqrt{3}x \; m \) と表すことができるので,
\( BH:PH=PH:AH \)
\( x:\sqrt{3}x=\sqrt{3}x:(x+10) \)
\( x(x+10)=3x^2 \)
\( 2x^2-10x=0 \)
\( x(x-5)=0 \)
\( x=5 \; (m) \) (\( x>0 \) より)
よって,\( PH=\sqrt{3} \times 5=5\sqrt{3} \; (m) \)
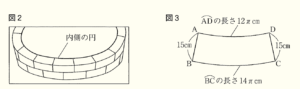
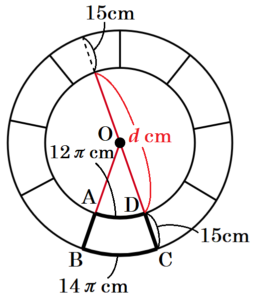
(4) 公園の花壇は円形であり,下の図2のように,同じ形のレンガを並べてつくられている。また,下の図3は,花壇を真上から見たときのレンガの1つで,直線 \( AB \) と直線 \( DC \) との交点を \( O \) とすると,おうぎ形 \( OBC \) からおうぎ形 \( OAD \) を取り除いた図形となっている。このとき,花壇の内側の円の直径は何 \( cm \) か求めよ。
【解説】
このレンガを \( x \) 個並べたとき,きれいな円ができるとすると,
内側の円の円周の長さは \( 12\pi{}x \; cm \)
外側の円の円周の長さは \( 14\pi{}x \; cm \)
と表すことができます。
また,内側の円の直径を \( d \; cm \) とすると,
外側の円の直径を \( d+30 \; cm \) と表すことができるので,
内側の円の円周の長さは \( \pi{}d \; cm \)
外側の円の円周の長さは \( \pi{}(d+30) \; cm \)
と表すことができます。
ここから,
内側の円の円周の長さの関係式は,\( 12\pi{}x=\pi{}d \) より,\( x=\dfrac{d}{12} \)
外側の円の円周の長さの関係式は,\( 14\pi{}x=\pi{}(d+30) \) より,\( x=\dfrac{d+30}{14} \)
よって,
\( \dfrac{d}{12}=\dfrac{d+30}{14} \)
\( 7d=6(d+30) \)
\( d=180 \; (cm) \)
大問4
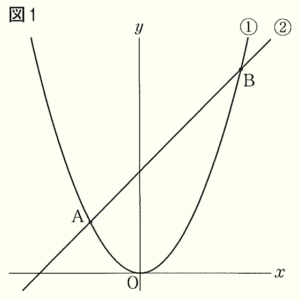
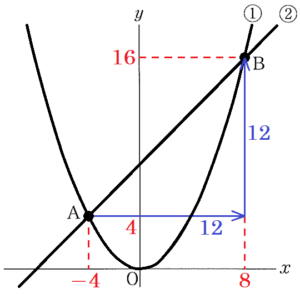
下の図1において,放物線 ① は関数 \( y=\dfrac{1}{4}x^2 \) のグラフであり,① 上の \( x \) 座標が \( −4,8 \) である点をそれぞれ \( A,B \) とする。また,直線 ② は2点 \( A,B \) を通る。
このとき,次の問いに答えなさい。
(1) \( y=\dfrac{1}{4}x^2 \) について,\( x \) の値が \( 4 \) から \( 8 \) まで増加するときの変化の割合を求めよ。
【解説】
\( x=4 \) のときの \( y \) の値は,
\( y=\dfrac{1}{4} \times 4^2=4 \)
\( x=8 \) のときの \( y \) の値は,
\( y=\dfrac{1}{4} \times 8^2=16 \)
なので,
変化の割合 \( =\dfrac{16-4}{8-4}=3 \)
(2) 直線 ② の式を求めよ。
【解説】
点 \( A \) の \( x \) 座標は \( x=-4 \) なので,
\( y \) 座標の値は,
\( y=\dfrac{1}{4} \times (-4)^2=4 \)
点 \( B \) の座標は \( (8,16) \) であることから,
直線 ➁ のの式を \( y=ax+b \) とすると,
\( a=\dfrac{16-4}{8-(-4)}=1 \)
\( y=x+b \) に \( x=8,y=16 \) を代入すると,
\( 16=8+b \)
\( b=8 \)
よって,求める直線の式は,\( y=x+8 \)
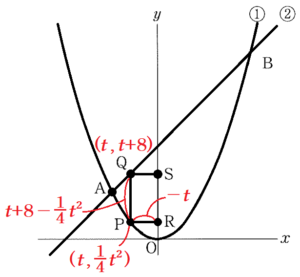
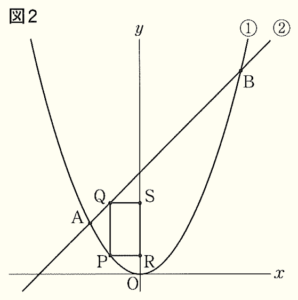
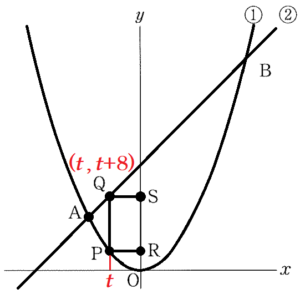
(3) 下の図2のように,点 \( P \) は,放物線 ① 上を,原点 \( O \) から点 \( A \) まで動く点とする。点 \( P \) を通り \( y \) 軸に平行な直線と直線 ➁ との交点を \( Q \) とし,点 \( P \) から \( y \) 軸にひいた垂線と \( y \) 軸との交点を \( R \),点 \( Q \) から \( y \) 軸にひいた垂線と \( y \) 軸との交点を \( S \) とする。また,点 \( P \) の \( x \) 座標を \( t \) とする。
ア 点 \( S \) の \( y \) 座標を \( t \) を使って表せ。
【解説】
点 \( P,Q \) の \( x \) 座標は \( t \) であり,
点 \( Q \) は \( y=x+8 \) 上の点なので,
\( y \) 座標は,\( y=t+8 \) と表すことができます。
点 \( Q,S \) の \( y \) 座標の値は等しいので,
点 \( S \) の \( y \) 座標は,\( y=t+8 \)
イ 四角形 \( PQSR \) が正方形となるとき,\( t \) の値を求めよ。
【解説】
点 \( P \) は \( y=\dfrac{1}{4}x^2 \) 上の点で,\( x \) 座標が \( t \) なので,
\( y \) 座標は \( \dfrac{1}{4}t^2 \) と表すことができ,
ここから,線分 \( PQ \) の長さは,
\( t+8-\dfrac{1}{4}t^2 \) と表すことができます。
また,線分 \( PR \) の長さは,\( -t \) と表すことができ,
正方形はすべての辺の長さが等しいので,
\( t+8-\dfrac{1}{4}t^2=-t \)
\( 4t+32-t^2=-4t \)
\( t^2-8t-32=0 \)
\( t=4-4\sqrt{3} \) (\( t<0 \) より)
 線分 \( PR \) の長さは正の数であり,
線分 \( PR \) の長さは正の数であり,
\( t<0 \) であることから,
線分 \( PR \) の長さは,\( -t \) になります。
大問5
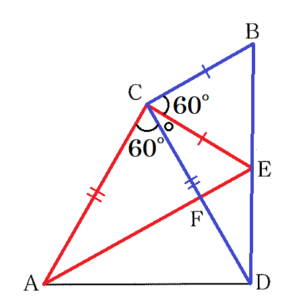
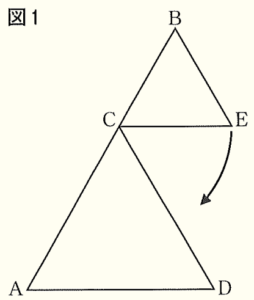
下の図1のように,線分 \( AB \) 上に点 \( C \) を,\( AC>CB \) となるようにとり,\( AC,CB \) をそれぞれ1辺とする正三角形 \( CAD, BCE \) を 直線 \( AB \) について同じ側につくる。この状態から,\( △BCE \) を,点 \( C \) を回転の中心として時計回りに回転させる。
このとき,次の問いに答えなさい。
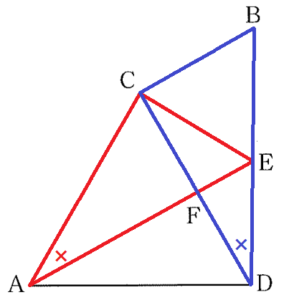
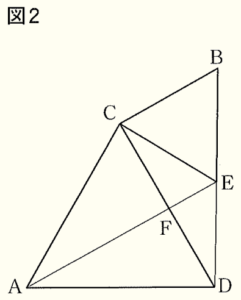
1 下の図2のように,点 \( E \) が線分 \( BD \) 上にあるとき,線分 \( AE \) と線分 \( CD \) との交点を \( F \) とする。
このとき
(1) \( △CAE≡△CDB \) であることを証明せよ。
【解答】
\( △CAE \) と \( △CDB \) において
\( △CAD \) は正三角形なので,\( CA=CD \) ・・・ ➀
\( △BCE \) は正三角形なので,\( CE=CB \) ・・・ ➁
\( △CAD,△BCE \) は正三角形なので,
\( ∠ACD=∠ECB=60° \) であり,
\( ∠ACE=∠ACD+∠DCE=60°+∠DCE \) ・・・ ➂
\( ∠DCB=∠ECB+∠DCE=60°+∠DCE \) ・・・ ➃
➂➃より,\( ∠ACE=∠DCB \) ・・・ ➄
➀➁➄より,2組の辺とその間の角がそれぞれ等しいので,
\( △CAE≡△CDB \)
(2) 次のア~エのうち,1つの円周上にある4点の組として正しいものを1つ選び,ア~エの記号で書け。
ア \( A,B,C,D \) イ \( A,B,C,F \)
ウ \( A,C,D,E \) エ \( B,C,E,F \)
【解説】
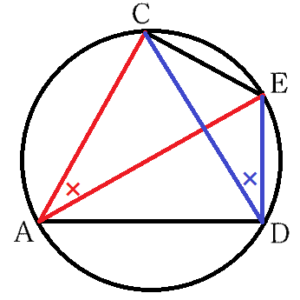
4点 \( A,C,D,E \) が1つの円周上にあると仮定すると,
\( ∠CAE,∠CDE \) は弧 \( CE \) に対する円周角になるので,
\( ∠CAE=∠CDE \) になります。
(1)より,\( △CAE≡△CDB \) であることから,
\( ∠CAE=∠CDB(∠CDE) \) なので,
4点 \( A,C,D,E \) が1つの円周上にあるといえます。
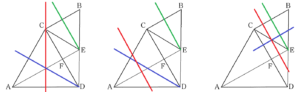
ア,イ,エがあてはまらない理由を「簡単に」考えてみる
1つの円において,すべての弦の垂直二等分線は,その円の中心で交わります。
ア,
イ,
エでは,各線分の垂直二等分線が1点で交わらないので,1つの円周上にはないといえます。
ア \( A,B,C,D \) イ \( A,B,C,F \) エ \( B,C,E,F \)
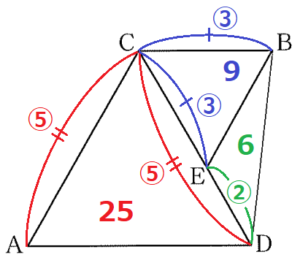
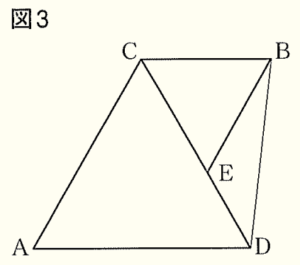
2 下の図3のように,点 \( E \) が辺 \( CD \) 上にある。\( AC:CB=5:3 \) のとき,四角形 \( ADBC \) の面積は,\( △BED \) の面積の何倍か求めよ。
【解答】
\( \dfrac{20}{3} \) 倍
【解説】
\( △CAD,△BCE \) は正三角形なので,\( △CAD \) ∽ \( △BCE \)
\( AC:CB=5:3 \) より,\( △CAD \) と \( △BCE \) の面積比は,
\( △CAD:△BCE=5^2:3^2=25:9 \) ・・・ ➀
\( △BCE \) と \( △BED \) は高さが共通の三角形なので,
\( △BCE:△BED=CE:ED \) となります。
\( CD:CE=AC:CB=5:3 \) なので,
\( CE:ED=3:2 \) であり,
\( △BCE:△BED=CE:ED=3:2=9:6 \) ・・・ ➁
➀➁より,\( △CAD:△BCE:△BED=25:9:6 \) なので,
\( △BED \) の面積を「6」とすると,
四角形 \( ADBC \) の面積は,
\( △CAD+△BCE+△BDE=25+9+6=40 \)
より,「40」になります。
よって,四角形 \( ADBC \) の面積は,\( △BED \) の面積の \( \dfrac{40}{6}=\dfrac{20}{3} \) 倍になります。







 線分 \( PR \) の長さは正の数であり,
線分 \( PR \) の長さは正の数であり,