大問1
(1) \( -3-(-9) \) を計算しなさい。
【解説】
\( =-3+9 \)
\( =6 \)
(2) \( 20xy^2 \div (-4xy) \) を計算しなさい。
(3) \( 4\sqrt{3}-\sqrt{12} \) を計算しなさい。
【解説】
\( =4\sqrt{3}-2\sqrt{3} \)
\( =2\sqrt{3} \)
(4) \( x^2+2x-8 \) を因数分解しなさい。
(5) \( y \) は \( x \) に反比例し,\( x=-6 \) のとき \( y=2 \) である。\( y=3 \) のときの \( x \) の値を求めなさい。
【解説】
反比例の式を \( y=\dfrac{a}{x} \) とし,\( x=-6,y=2 \) を代入すると,
\( 2=\dfrac{a}{-6} \)
\( a=-12 \)
よって,\( y=-\dfrac{12}{x} \) に \( y=3 \) を代入すると,
\( 3=-\dfrac{12}{x} \)
\( 3x=-12 \)
\( x=-4 \)
(6) 図1のように,底面の半径が \( 3 \; cm \),母線の長さが \( 6 \; cm \) の円すいがある。この円すいの側面積は何 \( cm^2 \) か,求めなさい。ただし,円周率は \( \pi{} \) とする。
【解答】
\( 18\pi{} \; cm^2 \)
【解説】
円すいの頂点を点 \( A \),底面の円の中心を点 \( O \) し,
展開すると,側面は右の図のようなおうぎ形になります。
側面のおうぎ形の弧の長さは底面の円周の長さと等しくなるので,
\( 2\pi{} \times 3=6\pi{} \; (cm) \)
母線を半径とする円周の長さは
\( 2\pi{} \times 6=12\pi{} \; (cm) \)
となるので,このおうぎ形の中心角は,
\( \dfrac{6\pi{}}{12\pi{}} \times 360°=180° \)
よって,側面積は,
\( \pi{} \times 6^2 \times \dfrac{180°}{360°}=18\pi{} \; (cm^2) \)
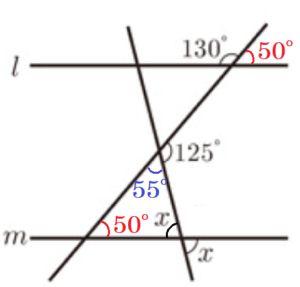
(7) 図2で, \( l//m \) のとき,\( x \) の大きさは何度か,求めなさい。
【解説】
\( ∠x+50°+55°=180° \)
\( ∠x=75° \)
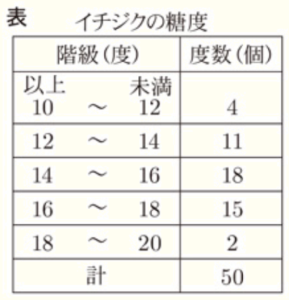
(8) 表は,ある農園でとれたイチジク1000個から,無作為に抽出したイチジク50個の糖度を調べ,その結果を度数分布表に表したものである。この結果から,この農園でとれたイチジク1000個のうち,糖度が10度以上14度未満のイチジクは,およそ何個と推定されるか,最も適切なものを,次の ア~エ から1つ選んで,その符号を書きなさい。
ア およそ150個
イ およそ220個
ウ およそ300個
エ およそ400個
【解説】
無作為に抽出したとき,分布の割合は全体と同じであると考えられます。
度数分布表から,10度以上14度未満のものの割合は \( \dfrac{4+11}{50}=\dfrac{15}{50} \) なので,
全体が1000個の場合は,\( 1000 \times \dfrac{15}{50}=300 \)(個)
大問2
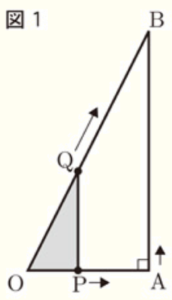
図1のように, \( OA=2 \; cm,AB=4 \; cm,∠OAB=90° \) の直角三角形 \( OAB \) がある。2点 \( P,Q \) は同時に \( O \) を出発し,それぞれ次のように移動する。
【点 \( P \) 】
・ 辺 \( OA \) 上を \( O \) から \( A \) まで秒速 \( 1 \; cm \) の速さで移動する。
・ \( A \) に着くと,辺 \( OA \) 上を移動するときとは速さを変えて,
辺 \( AB \) 上を \( A \) から \( B \) まで一定の速さで移動し,\( B \) に着くと
停止する。
【点 \( Q \) 】
・ 辺 \( OB \) 上を \( O \) から \( B \) まで,線分 \( PQ \) が \( OA \) と垂直に
なるように移動し,\( B \) に着くと停止する。
2点 \( P,Q \) が \( O \) を出発してから \( x \) 秒後の \( △OPQ \) の面積を \( y \; cm^2 \) とする。ただし,2点 \( P,Q \) が \( O \) にあるとき,および,2点 \( P,Q \) が \( B \) にあるとき,\( △OPQ \) の面積は \( 0 \; cm^2 \) とする。
次の問いに答えなさい。
(1) 2点 \( P,Q \) が \( O \) を出発してから1秒後の線分 \( PQ \) の長さは何 \( cm \) か,求めなさい。
【解説】
\( △OPQ \) と \( △OAB \) は相似で,\( OA:AB=2:4=1:2 \) になっています。
出発してから1秒後には \( OP=1 \; cm \) なので,\( PQ=2 \; cm \)
(2) \( 0≦x≦2 \) のとき,\( x \) と \( y \) の関係を表したグラフとして最も適切なものを,次の ア~エ から1つ選んで,その符号を書きなさい。

【解説】
\( 0≦x≦2 \) の範囲において,出発してから \( x \) 秒後の,\( OP,PQ \) の長さは,
\( OP=x \; cm,PQ=2x \; cm \) と表せるので,
\( △OPQ \) の面積は,\( y=x \times 2x \times \dfrac{1}{2}=x^2 \) となります。
よって,あてはまるグラフは ア になります。
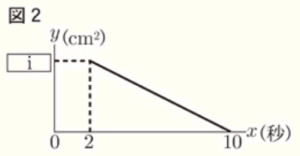
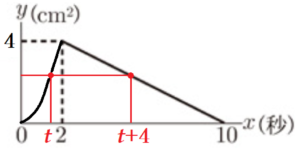
(3) \( 2≦x≦10 \) のとき,\( x \) と \( y \) の関係を表したグラフは図2のようになる。
➀ 図2の \( \fbox{ i } \) にあてはまる数を求めなさい。
【解説】
\( x=2 \) のとき,点 \( P \) は点 \( A \) の位置に,点 \( Q \) は点 \( B \) の位置にあります。
よって,\( x=2 \) のときの \( y \) の値は,
\( y=OA \times AB \times \dfrac{1}{2} \)
\( =2 \times 4 \times \dfrac{1}{2} \)
\( =4 \)
➁ 点 \( P \) が \( AB \) 上を移動するとき,点 \( P \) の速さは秒速何 \( cm \) か,求めなさい。
【解答】
秒速 \( \dfrac{1}{2} \; cm \)
【解説】
図2 から,\( x=10 \) のとき,2点 \( P,Q \) がともに点 \( B \) にあるとわかります。
ここから,点 \( P \) は \( x=2 \) のときに点 \( A \) を出発し,\( x=10 \) のときに点 \( B \) に到着したことになります。
よって,点 \( P \) は \( AB=4 \; cm \) を \( 8 \) 秒かけて進んだので,
その速さは,毎秒 \( 4 \div 8=\dfrac{1}{2} \; (cm) \) になります。
➂ 2点 \( P,Q \) が \( O \) を出発してから \( t \) 秒後の \( △OPQ \) の面積と,\( (t+4) \) 秒後の \( △OPQ \) の面積が等しくなる。このとき,\( t \) の値を求めなさい。ただし,\( 0<t<6 \) とする。
【解答】
\( t=\dfrac{3}{2} \)
【解説】
図2 に \( 0≦x≦2 \) のときの曲線を書き足してみます。
\( t \) 秒後の \( y \) の値と \( (t+4) \) 秒後の \( y \) の値が等しくなるので,\( 0<t<2 \) とわかります。
\( 0≦x≦2 \) のときの曲線の式は \( y=x^2 \) なので,
\( x=t \) を代入すると,\( y=t^2 \)
\( 2≦x≦10 \) のときの直線の式は \( y=-\dfrac{1}{2}x+5 \) なので,
\( x=t+4 \) を代入すると,\( y=-\dfrac{1}{2}(t+4)+5 \)
よって,
\( t^2=-\dfrac{1}{2}(t+4)+5 \)
\( t^2=-\dfrac{1}{2}t+3 \)
\( 2t^2+t-6=0 \)
\( (2t-3)(t+2)=0 \)
\( t=\dfrac{3}{2} \) (\( t>0 \) より)
大問3
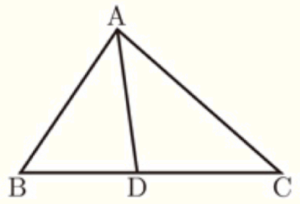
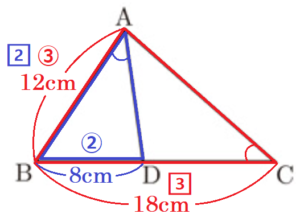
図のように,\( AB=12 \; cm,BC=18 \; cm \) の \( △ABC \) がある。\( ∠BAC \) の二等分線と辺 \( BC \) の交点を \( D \) とすると,\( BD=8 \; cm \) となる。
次の問いに答えなさい。
(1) \( ∠ACD=∠CAD \) であることを次のように証明した。
ⅰ , ⅱ にあてはまるものを,あとの ア~カ からそれぞれ1つ選んでその符号を書き,この証
明を完成させなさい。
<証明>
まず,\( △ABC \) ∽ \( △DBA \) であることを証明する。
\( △ABC \) と \( △DBA \) において,
仮定から,\( AB:DB=3:2 \) ・・・ ➀
ⅰ \( =3:2 \) ・・・ ➁
➀,➁より,
\( AB:DB= \) ⅰ ・・・ ➂
共通な角だから,
\( ∠ABC=∠DBA \) ・・・ ➃
➂,➃より,
2組の辺の比とその間の角がそれぞれ等しいから,
\( △ABC \) ∽ \( △DBA \)
したがって,\( ∠ACB=∠ \) ⅱ ・・・ ➄
仮定から, \( ∠ \) ⅱ \( =∠DAC \) ・・・ ⑥
➄,➅より,\( ∠ACD=∠CAD \)
ア \( BC:BA \) イ \( BA:BC \) ウ \( BC:DB \)
エ \( ABD \) オ \( DAB \) カ \( ADB \)
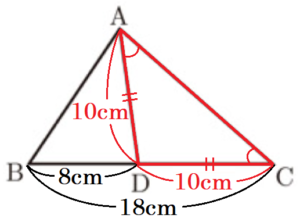
(2) 線分 \( AD \) の長さは何 \( cm \) か,求めなさい。
【解説】
(1)より,\( ∠ACD=∠CAD \) なので,
\( △ACD \) は \( AD=CD \) の二等辺三角形になっています。
\( BD=8 \; cm,BC=18 \; cm \) より,
\( CD=18-8=10 \; (cm) \) なので,
\( AD=CD=10 \; (cm) \)
(3) 線分 \( AC \) の長さは何 \( cm \) か,求めなさい。
【解説】
(1)より,\( △ABC \) ∽ \( △DBA \) で相似比は \( 3:2 \) なので,
\( AC:DA=3:2 \)
\( AC:10=3:2 \)
\( AC=15 \; (cm) \)

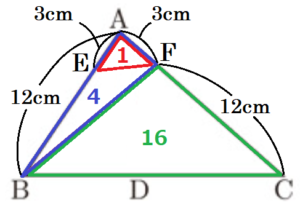
(4) 辺 \( AB \) 上に,\( DE=8 \; cm \) となるように,点 \( B \) と異なる点 \( E \) をとる。また,辺 \( AC \) 上に点 \( F \) をとり,\( AE,AF \) をとなり合う辺とするひし形をつくる。このひし形の面積は,\( △ABC \) の面積の何倍か,求めなさい。
【解答】
\( \dfrac{1}{10} \) 倍
【解説】
「\( AE,AF \) をとなり合う辺とするひし形をつくる」ということは,\( △AEF \) の面積はひし形の面積の半分になります。
このことから,まず,\( △AEF \) と \( △ABC \) の面積比を求めてから,ひし形と \( △ABC \) の面積比を求めることにします。
\( △AED \) と \( △AFD \) において,
ひし形のすべての辺の長さは等しいので,
\( AE=AF \)
線分 \( AD \) は \( ∠BAC \) の二等分線なので,
\( ∠EAD=∠FAD \)
線分 \( AD \) は共通
よって,
2組の辺とその間の角がそれぞれ等しいので,
\( △AED≡△AFD \)
また,
\( ∠BED \) は \( △AED \) の外角なので,
\( ∠BED=∠EAD+∠ADE \)
\( ∠CFD \) は \( △AFD \) の外角なので,
\( ∠CFD=∠FAD+∠ADF \)
\( ∠EAD=∠FAD,∠ADE=∠ADF \) より,
\( ∠BED=∠CFD \)
\( △DBE \) は二等辺三角形で底角は等しいので,
\( ∠BED=∠EBD \) であり,
\( ∠BED=∠CFD \) より,\( ∠EBD=∠CFD \)
\( △ABD \) と \( △CFD \) において,
\( ∠ABD=∠CFD,∠BAD=∠FCD \) より,
のこり1つの角も等しいので,\( ∠ADB=∠CDF \)
\( AD=CD=10 \; cm \) より,
1組の辺とその両端の角がそれぞれ等しいので,
\( △ABD≡△CFD \)
対応する辺の長さは等しいので,
\( CF=AB=12 \; cm \)
\( AC=15 \; cm \) より,\( AF=AC-CF=3 \; cm \)
ここで,\( △AEF \) の面積を1とすると,
\( △AEF:△ABF=AE:AB=3:12=1:4 \)
\( △ABF:△CBF=AF:CF=3:12=4:16 \)
より,\( △ABF \) の面積は4,\( △CBF \) の面積は16となるので,
\( △ABC=△ABF+△CBF=20 \)
ひし形の面積は\( △AEF \) の面積の2倍なので,2となります。
以上より,ひし形の面積は \( \dfrac{2}{20}=\dfrac{1}{10} \) 倍
大問4
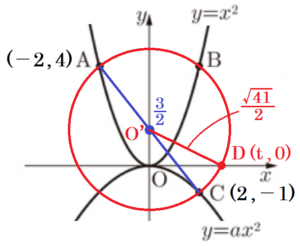
図のように,関数 \( y=x^2 \) のグラフ上に異なる2点 \( A,B \) があり,関数 \( y=ax^2 \) のグラフ上に点 \( C \) がある。点 \( C \) の座標は \( (2,-1) \) であり,点 \( A \) と点 \( B \) の \( y \) 座標は等しく,点 \( B \) と点 \( C \) の \( x \) 座標は等しい。
次の問いに答えなさい。ただし,座標軸の単位の長さは \( 1 \; cm \) とする。
(1) 点 \( A \) の \( x \) 座標を求めなさい。
【解説】
点 \( B \) と点 \( C \) の \( x \) 座標は等しいので,点 \( C \) の \( x \) 座標は \( 2 \) になります。
また,点 \( A \) と点 \( B \) の \( y \) 座標は等しいことから,
点 \( A \) の \( x \) 座標は,点 \( B \) の \( x \) 座標の符号を変えたものになるので,\( -2 \)
(2) \( a \) の値を求めなさい。
【解答】
\( a=-\dfrac{1}{4} \)
【解説】
\( y=ax^2 \) に \( x=2,y=-1 \) を代入すると,
\( -1=a \times 2^2 \)
\( a=-\dfrac{1}{4} \)
(3) 直線 \( AC \) の式を求めなさい。
【解答】
\( y=-\dfrac{5}{4}x+\dfrac{3}{2} \)
【解説】
点 \( A \) の座標は,\( (-2,4) \) なので,
直線 \( AC \) の傾きは,
傾き \( =\dfrac{-1-4}{2-(-2)}=-\dfrac{5}{4} \)
直線 \( AC \) の式を \( y=-\dfrac{5}{4}x+b \) とし,\( x=2,y=-1 \) を代入すると,
\( -1=-\dfrac{5}{4} \times 2+b \)
\( -1=-\dfrac{5}{2}+b \)
\( b=\dfrac{3}{2} \)
よって,直線 \( AC \) の式は \( y=-\dfrac{5}{4}x+\dfrac{3}{2} \)
(4) 3点 \( A,B,C \) を通る円を円 \( O′ \) とする。
➀ 円 \( O′ \) の直径の長さは何 \( cm \) か,求めなさい。
【解答】
\( \sqrt{41} \; cm \)
【解説】
3点 \( A,B,C \) は円 \( O′ \) の円周上にあるので,
\( ∠ABC=90° \) より,\( ∠ABC \) は直径 \( AC \) に対する円周角となります。
\( A(-2,4),B(2,4),C(2,-1) \) より,
\( AB=4 \; cm,BC=5 \; cm \) なので,
\( AC^2=AB^2+BC^2=41 \)
\( AC=\sqrt{41} \; (cm) \) (\( AC>0 \) より)
➁ 円 \( O′ \) と \( x \) 軸との交点のうち,\( x \) 座標が正の数である点を \( D \) とする。点 \( D \) の \( x \) 座標を求めなさい。
【解説】
点 \( D \) は円 \( O′ \) 上の点なので,線分 \( O’D \) は円 \( O′ \) の半径になります。
ここから,中心 \( O′ \) の座標を求めると,
三平方の定理を使って,点 \( D \) の \( x \) 座標を求めることができます。
線分 \( AC \) は円 \( O′ \) の直径なので,
中心 \( O′ \) は線分 \( AC \) の中点になります。
中心 \( O′ \) の
\( x \) 座標は,\( \dfrac{-2+2}{2}=0 \),
\( y \) 座標は,\( \dfrac{4+(-1)}{2}=\dfrac{3}{2} \)
となるので,\( OO’=\dfrac{3}{2} \; cm \)
点 \( D \) の座標を \( (t,0) \) とすると,\( OD=t \; cm \)
直径 \( AC=\sqrt{41} \; cm \) より,半径 \( O’D=\dfrac{\sqrt{41}}{2} \; cm \) なので,
三平方の定理より,
\( O’D^2=OO’^2+OD^2 \)
\( \left( \dfrac{\sqrt{41}}{2} \right)^2=\left( \dfrac{3}{2} \right)^2+t^2 \)
\( \dfrac{41}{4}=\dfrac{9}{4}+t^2 \)
\( t^2=8 \)
\( t=2\sqrt{2} \) (\( t>0 \) より)
大問5
さいころが1つと大きな箱が1つある。また,\( 1,2,3,4,5,6 \) の数がそれぞれ1つずつ書かれた玉がたくさんある。箱の中が空の状態から,次の【操作】を何回か続けて行う。そのあいだ,箱の中から玉は取り出さない。
あとの問いに答えなさい。ただし,玉は【操作】を続けて行うことができるだけの個数があるものとする。また,さいころの \( 1 \) から \( 6 \) までのどの目が出ることも同様に確からしいとする。
【操作】
(ⅰ) さいころを1回投げ,出た目を確認する。
(ⅱ) 出た目の約数が書かれた玉を,それぞれ1個ずつ箱の中に入れる。
例:(ⅰ)で \( 4 \) の目が出た場合は,(ⅱ)で \( 1,2,4 \) が書かれた玉をそれぞれ1個ずつ箱の中に入れる。
(1) (i)で \( 6 \) の目が出た場合は,(ⅱ)で箱の中に入れる玉は何個か,求めなさい。
【解説】
\( 6 \) の約数は \( 1,2,3,6 \) の4つなので,箱の中に入れる玉は4個
(2) 【操作】を2回続けて行ったとき,箱の中に4個の玉がある確率を求めなさい。
【解答】
\( \dfrac{11}{36} \)
【解説】
さいころの出た目によって,箱の中に入れる玉は何個になるかを確認します。
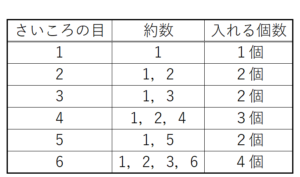
ここから,【操作】を2回続けて行ったとき,さいころの目の組み合わせによって,
箱の中に入れる球の個数が合計何個になるかを樹形図に書き出してみます。
箱の中に入れる球の個数が4個になる組み合わせは11通り,すべての組み合わせは36通りなので,
求める確率は \( \dfrac{11}{36} \)

(3) 【操作】を \( n \) 回続けて行ったとき,次のようになった。
・ \( n \) 回のうち,\( 1 \) の目が2回,\( 2 \) の目が5回出た。\( 3 \) の目が出た回数と \( 5 \) の目が出た回数は等しかった。
・ 箱の中には,全部で52個の玉があり,そのうち \( 1 \) が書かれた玉は21個であった。\( 4 \) が書かれた玉の個数と \( 6 \) が書かれた玉の個数は等しかった。
➀ \( n \) の値を求めなさい。
【解説】
さいころの目によらず,\( 1 \) が書かれた玉は必ず1個ずつ箱の中に追加されるので,
\( 1 \) が書かれた玉の個数と【操作】が行われた回数は等しくなります。
よって,【操作】が行われた回数は21回とわかります。

➁ \( 5 \) の目が何回出たか,求めなさい。
【解説】
問➀より,【操作】が行われたのは全部で21回です。
また,\( 4 \) が書かれた玉を入れるのは,\( 4 \) の目が出たときだけ,
\( 6 \) が書かれた玉を入れるのは,\( 6 \) の目が出たときだけなので,
玉の個数が等しいことから,\( 4 \) の目が出た回数と\( 6 \) の目が出た回数は等しかったとわかります。
よって,\( 3 \) の目が出た回数と \( 5 \) の目が出た回数をそれぞれ \( a \) 回,
\( 4 \) の目が出た回数と\( 6 \) の目が出た回数をそれぞれ \( b \) 回とし,
出た目の回数の関係を方程式にすると,\( 2a+2b=14 \) ・・・ ➀ となります。
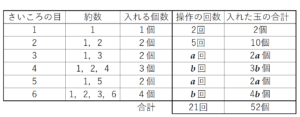
次に箱の中の玉の個数に注目すると,
21回の【操作】を行った結果,箱の中の玉の個数は,下の表のようになるので,
箱の中の玉の個数の関係を方程式にすると,\( 4a+7b=40 \) ・・・ ➁ となります。
よって,➀➁を連立方程式として解くと,
\( \left\{ \begin{array}{}
2a+2b=14 \;\; ・・・ \;\; ➀ \\
4a+7b=40 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁ \( – \) ➀ \( \times 2 \)
\( 3b=12 \)
\( b=4 \)
➀に代入すると,
\( 2a+2 \times 4=14 \)
\( a=3 \)
よって,\( 5 \) の目が出た回数は3回。
➂ 52個の玉のうち,\( 5 \) が書かれた玉を箱の中から全て取り出す。その後,箱の中に残った玉をよくかき混ぜてから,玉を1個だけ取り出すとき,その取り出した玉に書かれた数が \( 6 \) の約数である確率を求めなさい。ただし,どの玉が取り出されることも同様に確からしいとする。
【解答】
\( \dfrac{45}{49} \)
【解説】
\( 5 \) が書かれた玉を入れたのは,\( 5 \) の目が出たときだけなので,
問➁の結果から,箱の中に入っている \( 5 \) が書かれた玉の個数は3個であるとわかります。
この3個を取り除くと,残りの箱の中の玉は49個になります。
また,残りの \( 1,2,3,4,6 \) のうち, \( 1,2,3,6 \) が \( 6 \) の約数であり,
「\( 4 \) だけが \( 6 \) の約数ではない」ともいえます。
\( 4 \) が書かれた玉を入れたのは,\( 4 \) の目が出たときだけなので,
問➁の結果から,箱の中に入っている \( 4 \) が書かれた玉の個数は4個であり,
\( 1,2,3,6 \) のいずれかが書かれた玉の個数の合計は45個であるとわかります。
よって,\( 1,2,3,6 \) のいずれかが書かれた玉を選ぶ確率は \( \dfrac{45}{49} \)
大問6
数学の授業中に先生が手品を行い,ゆうりさんたち生徒は手品の仕掛けについて考察した。
あとの問いに答えなさい。
先 生:ここに3つの空の箱,箱A,箱B,箱Cと,たくさんのコインがあります。ゆうりさん,先生に
見えないように,黒板に示している作業1~4を順に行ってください。
作業1:箱A,箱B,箱Cに同じ枚数ずつコインを入れる。ただし,各箱に入れるコインの枚数は
20以上とする。
作業2:箱B,箱Cから8枚ずつコインを取り出し,箱Aに入れる。
作業3:箱Cの中にあるコインの枚数を数え,それと同じ枚数のコインを箱Aから取り出し,
箱Bに入れる。
作業4:箱Bから1枚コインを取り出し,箱Aに入れる。
ゆうり:はい。できました。
先 生:では,箱Aの中にコインが何枚あるか当ててみましょう。 a 枚ですね。どうですか。
ゆうり:数えてみます。 \( 1,2,3,・・・ , \) すごい! 確かにコインは a 枚あります。
(1) 作業1で, 箱A,箱B,箱Cに20枚ずつコインを入れた場合, a にあてはまる数を求めなさい。
【解説】
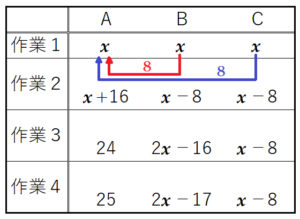
作業1~4を行ったときの箱A,箱B,箱Cに入っているコインの枚数を右の表のように書き出してみます。
(2) 授業後,ゆうりさんは「授業振り返りシート」を作成した。 ⅰ にあてはまる数, ⅱ , ⅲ にあてはまる式をそれぞれ求めなさい。
授業振り返りシート
授業日:3月10日 (金)
Ⅰ 授業で行ったこと
先生が手品をしてくれました。その手品の仕掛けを数学的に説明するために,グループで話し合いま
した。
Ⅱ わかったこと
作業1で箱A,箱B,箱Cに20枚ずつコインを入れても,21枚ずつコインを入れても,作業4の
後に箱Aの中にあるコインは a 枚となります。
なぜそのようになるかは,次のように説明できます。
・ 作業4の後に箱Aの中にコインが a 枚あるということは,作業3の後に箱Aの中にコイン
が ⅰ 枚あるということです。
・ 作業1で箱A,箱B,箱Cに \( x \) 枚ずつコインを入れた場合,作業2の後に箱Aの中にある
コインは \( x \) を用いて ⅱ 枚,箱Cの中にあるコインは \( x \) を用いて ⅲ 枚と表す
ことができます。つまり,作業3では ⅲ 枚のコインを箱Aから取り出すので, ⅱ から
ⅲ をひくと,\( x \) の値に関係なく ⅰ になります。
これらのことから,作業1で各箱に入れるコインの枚数に関係なく,先生は a 枚と言えば
よかったということです。
【解答】
ⅰ ・・・ 24
ⅱ ・・・ \( x+16 \)
ⅲ ・・・ \( x-8 \)
【解説】
ⅰ
(1)で作った表より,作業3の後の箱Aの中のコインの枚数は24枚
(1)と同様に,作業1で箱A,箱B,箱Cに \( x \) 枚ずつコインを入れた場合の表を書いてみます。
ⅲ
作業2では,箱Cから8枚コインを取り出すので,
取り出した後のコインの枚数は \( x-8 \) 枚になります。
ⅱ
作業2では,箱B,箱Cから8枚ずつコインを取り出し,その合計16枚を箱Aに入れるので,コインを入れた後の枚数は,\( x+16 \) 枚になります。
 注)ここでは,作業2までの枚数だけで解けます。
注)ここでは,作業2までの枚数だけで解けます。
(3) ゆうりさんは,作業2で箱B,箱Cから取り出すコインの枚数を変えて何回かこの手品を行い,作業3の後に箱Aの中にあるコインの枚数は必ず \( n \) の倍数となることに気がついた。ただし,作業2では箱B,箱Cから同じ枚数のコインを取り出し,箱Aに入れることとし,作業2以外は変更しない。また,各作業中,いずれの箱の中にあるコインの枚数も \( 0 \) になることはないものとする。
➀ \( n \) の値を求めなさい。ただし,\( n \) は \( 1 \) 以外の自然数とする。
【解説】
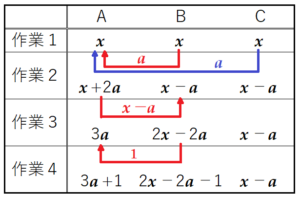
作業2で箱B,箱Cから取り出すコインの枚数を \( a \) 枚として,同様に表を書いてみます。
作業2を終えた後,
箱Aのコインの枚数は \( x+2a \) 枚,
箱Cのコインの枚数は \( x-a \) 枚
になります。
作業3では,
箱Aからコインを \( x-a \) 枚取り出すので,
取り出した後のコインの枚数は,
\( (x+2a)-(x-a)=3a \)(枚)となります。
\( a \) は自然数なので,\( 3a \) は \( 3 \) の倍数になります。
➁ 次の ア~ウ のうち,作業4の後に箱Aの中にあるコインの枚数として適切なものを,ゆうりさんの気づきをもとに1つ選んで,その符号を書きなさい。また,その枚数にするためには,作業2で箱B,箱Cから何枚ずつコインを取り出せばよいか,求めなさい。
ア \( 35 \) イ \( 45 \) ウ \( 55 \)
【解説】
作業4では,箱Aにコインを1枚入れるので,
作業4を終えた後,
箱Aのコインの枚数は \( 3a+1 \) 枚になります。
つまり,作業4を終えた後の箱Aのコインの枚数は
3の倍数より1大きい数になります。
よって,
ア ・・・ \( 35=3 \times 11+2 \)
イ ・・・ \( 45=3 \times 15 \)
ウ ・・・ \( 55=3 \times 18+1 \)
なので,あてはまるのは ウ で,
そのときの \( a \) の値は,\( a=18 \) になります。















 注)ここでは,作業2までの枚数だけで解けます。
注)ここでは,作業2までの枚数だけで解けます。
-アイキャッチ-120x68.jpg)
-アイキャッチ-120x68.jpg)