大問1
(1) 次のア~オの計算をしなさい。
ア \( 7-(-2) \)
イ \( 2^3+8 \div (-4) \)
【解説】
\( =8+8 \div (-4) \)
\( =8+(-2) \)
\( =8-2 \)
\( =6 \)
ウ \( (-3xy)^2 \div \dfrac{12}{5}xy^2 \)
【解答】
\( \dfrac{15}{4}x \)
【解説】
\( =9x^2y^2 \times \dfrac{5}{12xy^2} \)
\( =\dfrac{9x^2y^2 \times 5}{12xy^2} \)
\( =\dfrac{15x}{4} \)
エ \( \dfrac{5a+b}{3}-\dfrac{a-b}{2} \)
【解答】
\( \dfrac{7a+5b}{6} \)
【解説】
\( =\dfrac{2(5a+b)}{6}-\dfrac{3(a-b)}{6} \)
\( =\dfrac{2(5a+b)-3(a-b)}{6} \)
\( =\dfrac{10a+2b-3a+3b}{6} \)
\( =\dfrac{7a+5b}{6} \)
オ \( \sqrt{18}-8\sqrt{5} \times \dfrac{1}{\sqrt{10}} \)
【解説】
\( =3\sqrt{2}-8\sqrt{5} \times \dfrac{1}{\sqrt{10}} \)
\( =3\sqrt{2}-8\sqrt{5} \times \dfrac{1}{\sqrt{2} \times \sqrt{5}} \)
\( =3\sqrt{2}-\dfrac{8}{\sqrt{2}} \)
\( =3\sqrt{2}-\dfrac{8 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} \)
\( =3\sqrt{2}-4\sqrt{2} \)
\( =-\sqrt{2} \)
(2) 次の方程式を解きなさい。
\( x^2-7x+2=0 \)
【解答】
\( x=\dfrac{7±\sqrt{41}}{2} \)
【解説】
解の公式より,
\( x=\dfrac{-(-7)±\sqrt{(-7)^2-4 \times 1 \times 2}}{2 \times 1} \)
\( =\dfrac{7±\sqrt{41}}{2} \)
(3) \( 8<\sqrt{n}<8.2 \) をみたす自然数 \( n \) の値をすべて求めなさい。
【解説】
3つの数 \( a,b,c \) が \( a<b<c \) の関係にあるとき,
\( a,b,c \) それぞれを2乗しても大小の関係は変わりません。
\( 8,\sqrt{n},8.2 \) をそれぞれ2乗すると,\( 64,n,67.24 \) なので,
\( 64<n<67.24 \) の関係になっています。
よって,これをみたす自然数 \( n \) の値は \( 65,66,67 \) になります。
(4) 「*」の記号は,2つの数 \( a,b \) について,
\( a*b=ab-4b+5 \)
のように計算するものとする。
このとき,\( 3*(2x)=4 \) となる \( x \) の値を求めなさい。
【解答】
\( x=\dfrac{1}{2} \)
【解説】
\( a*b=ab-4b+5 \) に \( a=3,b=2x \) を代入すると,
\( 3*(2x)=3 \times 2x-4 \times 2x+5 \)
\( =6x-8x+5 \)
\( =-2x+5 \)
なので,\( 3*(2x)=4 \) の \( 3*(2x) \) を \( -2x+5 \) におきかえると,
\( -2x+5=4 \)
\( -2x=-1 \)
\( x=\dfrac{1}{2} \)
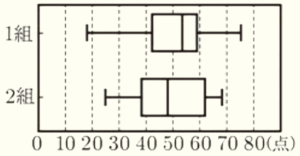
(5) A中学校の3年1組の生徒 \( 39 \) 人と2組の生徒 \( 38 \) 人に,体力テストを実施した。右の図は,体力テストの得点の分布のようすを箱ひげ図に表したものである。
このとき,次のア~エのうち,箱ひげ図から読みとれることとして正しいものを1つ選び,その符号を書きなさい。
ア 四分位範囲は,1組のほうが2組よりも大きい。
イ \( 20 \) 点以上 \( 70 \) 点未満の人数は,1組のほうが2組よりも多い。
ウ 第1四分位数は,2組のほうが1組よりも大きい。
エ \( 60 \) 点以上の人数は,2組のほうが1組よりも多い。
【解説】
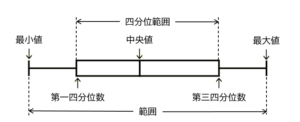
ア 四分位範囲が大きいほど,箱の長さが長くなります。
箱の長さは2組のほうが1組よりも長いので,四分位範囲は2組の方が大きくなっています。
イ 箱ひげ図から,1組の最小値は \( 20 \) 点未満,最大値が \( 70 \) 点より大きいので,
\( 20 \) 点以上 \( 70 \) 点未満の人数は,最大でも \( 37 \) 人です。
2組は最小値は \( 20 \) 点より大きく,最大値が \( 70 \) 点未満なので,
\( 38 \) 人全員が \( 20 \) 点以上 \( 70 \) 点未満です。
よって,\( 20 \) 点以上 \( 70 \) 点未満の人数は,2組のほうが1組よりも多くなっています。
ウ 箱ひげ図から,1組の第1四分位数は \( 40 \) 点より大きく,
2組の第1四分位数は \( 40 \) 点未満なので,
第1四分位数は,1組のほうが2組よりも大きくなっています。
エ 1組は \( 39 \) 人分のデータを集計しているので,第3四分位数は得点の高い方から
10番目の値になります。
1組の第3四分位数は \( 60 \) 点未満なので,\( 60 \) 点以上の人数は,
多くても \( 9 \) 人になります。
2組は \( 38 \) 人分のデータを集計しているので,第3四分位数は得点の高い方から
10番目の値になります。
2組の第3四分位数は \( 60 \) 点以上なので,\( 60 \) 点以上の人数は,
少なくても \( 10 \) 人になります。
よって,\( 60 \) 点以上の人数は,2組のほうが1組よりも多くなっています。
大問2
Aさん,Bさん,Cさんの3人が,1から6までの目が出るさいころを順番に1回ずつ投げて,出た目の数だけ自分のコマを進める「すごろく」をする。
このとき,次の(1),(2)に答えなさい。ただし,さいころはどの目が出ることも同様に確からしいとする。
(1) 3人がさいころを順番に1回ずつ投げるとき,この3人が投げる順番は全部で何通りあるか,求めなさい。
【解説】
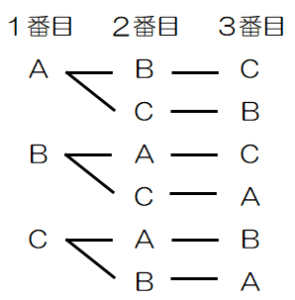
3人が投げる順番を樹形図に書き出すと,次の6通りになります。
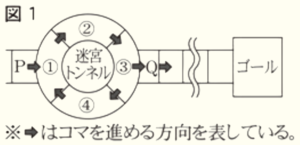
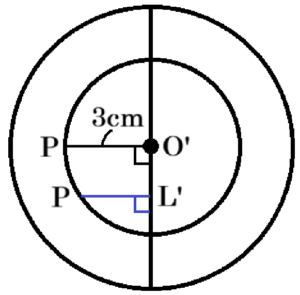
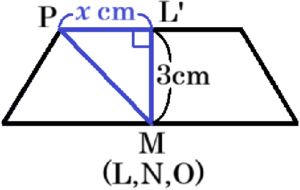
(2) 図1は,3人がしている「すごろく」の一部であり,AさんのコマとBさんのコマがともに \( P \) のマスにある。\( P \) のマスと \( Q \) のマスの間には,➀,➁,➂,➃の4つのマスからなる「迷宮トンネル」があり,この「迷宮トンネル」には次の規則がある。
<規則>
・ ➀ → ➁ → ➂ → ➃ → ➀ → ➁ → ・・・ と時計回りにコマを進める。
・ ➂ のマスにコマが止まったときだけ,次にさいころを投げた後に,コマをQのマスを通って
ゴールの方向に進めることができる。
また,図2のように「おたすけカードX」と「おたすけカードY」があり,カードを持っていればさいころを投げる直前に使うことができる。Aさんは「おたすけカードX」を,Bさんは「おたすけカードY」を持っており,AさんもBさんもそれぞれ持っているカードを使うことにした。

このとき,AさんとBさんのそれぞれのコマが ➂ のマスに止まる確率について,次のア~ウから正しいものを1つ選び,その符号を書きなさい。また,選んだ理由も説明しなさい。説明においては,図や表,式などを用いてよい。
ア Aさんの確率のほうがBさんより大きい。
イ Bさんの確率のほうがAさんより大きい。
ウ AさんとBさんの確率は等しい。
【解答】
ア
【Aさんの確率】
移動先が ➂ になるのは,出た目が2または6のときなので,
あてはまる確率は \( \dfrac{2}{6}=\dfrac{1}{3} \)
【Bさんの確率】
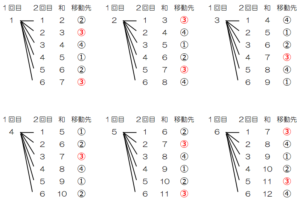
さいころを2回投げたときの出た目の組み合わせとそれぞれの場合の行き先を樹形図として書き出すと
下の図のようになります。
すべての場合の数は \( 36 \) 通り,移動先が➂になる組み合わせは \( 10 \) 通りなので,
求める確率は \( \dfrac{10}{36}=\dfrac{5}{18} \)
よって,Aさんの確率のほうがBさんより大きい。
【解説】
【Aさんの確率】
さいころの目が1の場合 → 移動先は➁
さいころの目が2の場合 → 移動先は➂
さいころの目が3の場合 → 移動先は➃
さいころの目が4の場合 → 移動先は➀
さいころの目が5の場合 → 移動先は➁
さいころの目が6の場合 → 移動先は➂
なので,移動先が➂になる確率は \( \dfrac{2}{6}=\dfrac{1}{3} \)
大問3
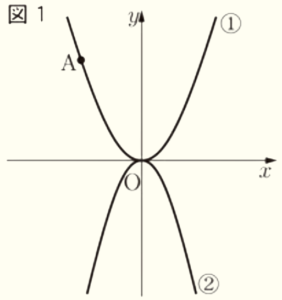
図1~3において,➀は関数 \( y=ax^2 \),➁は関数 \( y=-x^2 \) のグラフである。
このとき,次の(1)~(3)に答えなさい。
(1) 図1において,➀のグラフ上の点 \( A \) の座標が \( (-3,5) \) であるとき,\( a \) の値を求めなさい。
【解答】
\( a=\dfrac{5}{9} \)
【解説】
点 \( A \) は \( y=ax^2 \) 上の点で,\( x=-3,y=5 \) なので,
\( 5=a \times (-3)^2 \)
\( a=\dfrac{5}{9} \)
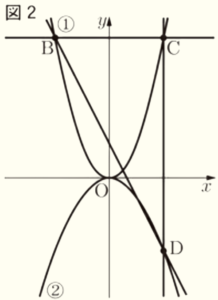
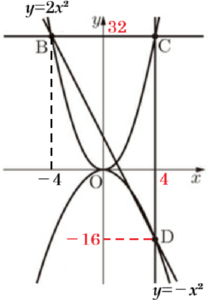
(2)\( a=2 \) とする。図2において,点 \( B \) は➀のグラフ上の点であり,\( x \) 座標は \( -4 \) である。また,点 \( B \) を通り \( x \) 軸に平行な直線と➀のグラフとの交点のうち,\( B \) と異なる点を \( C \) とし,点 \( C \) を通り \( y \) 軸に平行な直線と➁のグラフとの交点を \( D \) とする。
このとき,直線 \( BD \) の式を求めなさい。
【解説】
点 \( B \) は \( y=2x^2 \) 上の点で,\( x=-4 \) なので,
\( y=2 \times (-4)^2=32 \)
点 \( B、C \) は \( y \) 座標が等しいことから,
点 \( C \) は \( y \) 軸に対して点 \( B \) と対称な点なので,\( C( 4,32) \)
点 \( D \) は \( y=-x^2 \) 上の点で,\( x=4 \) なので,
\( y=-4^2=-16 \)
直線 \( BD \) は \( B\left( -4,32 \right),D( 4,-16) \) を通るので,
直線 \( BD \) の式を \( y=mx+n \) とすると,
\( m=\dfrac{-16-32}{4-(-4)} \)
\( =-6 \)
\( y=-6x+n \) に \( x=4,y=-16 \) を代入すると,
\( -16=-6 \times 4+n \)
\( n=8 \)
よって,直線 \( BD \) の式は \( y=-6x+8 \)
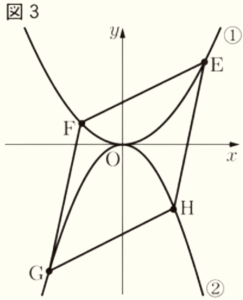
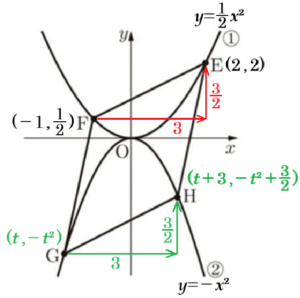
(3) \( a=\dfrac{1}{2} \) とする。図3において,点 \( E,F \) は➀のグラフ上の点であり,\( x \) 座標はそれぞれ \( 2,-1 \) である。また,点 \( G,H \) は➁のグラフ上の点であり,四角形 \( EFGH \) は平行四辺形である。
このとき,点 \( G \) の座標を求めなさい。なお,途中の計算も書くこと。
【解答】
2点 \( E,F \) の座標はそれぞれ \( E(2,2),F \left( -1,\dfrac{1}{2} \right) \) なので,
点 \( G \) の \( x \) 座標を \( t \) とすると,
2点 \( G,H \) の座標はそれぞれ \( G(t,-t^2),H \left( t+3,-t^2+\dfrac{3}{2} \right) \) と表すことができる。
点 \( H \) は,\( y=-x^2 \) 上の点であることから,
\( -t^2+\dfrac{3}{2}=-(t+3)^2 \)
\( -t^2+\dfrac{3}{2}=-t^2-6t-9 \)
\( 6t=-\dfrac{21}{2} \)
\( t=-\dfrac{7}{4} \)
よって,点 \( G \) の座標は,\( G \left( -\dfrac{7}{4},-\dfrac{49}{16} \right) \)
【解説】
点 \( E \) は \( y=\dfrac{1}{2}x^2 \) 上の点で,\( x=-1 \) なので,
\( y=\dfrac{1}{2} \times (-1)^2=\dfrac{1}{2} \)
点 \( F \) は \( y=\dfrac{1}{2}x^2 \) 上の点で,\( x=2 \) なので,
\( y=\dfrac{1}{2} \times 2^2=2 \)
点 \( G \) の \( x \) 座標を \( t \) とすると,\( y=-x^2 \) 上の点
なので,\( y \) 座標は \( -t^2 \) と表すことができます。
平行四辺形の向かい合う辺は平行で長さが等しいので,
点 \( F \) が,点 \( E \) から \( x \) 方向に \( 3,y \) 方向に \( \dfrac{3}{2} \) 移動した点であることから,
点 \( H \) は,点 \( G \) から \( x \) 方向に \( 3,y \) 方向に \( \dfrac{3}{2} \) 移動した点になります。
ここから,点 \( H \) の座標は,\( H \left( t+3,-t^2+\dfrac{3}{2} \right) \) と表すことができます。
点 \( H \) は,\( y=-x^2 \) 上の点であることから,\( x \) に \( t+3,y \) に,\( -t^2+\dfrac{3}{2} \) を代入すると,
\( -t^2+\dfrac{3}{2}=-(t+3)^2 \)
\( -t^2+\dfrac{3}{2}=-t^2-6t-9 \)
\( 6t=-\dfrac{21}{2} \)
\( t=-\dfrac{7}{4} \)
よって,点 \( G \) の座標は,\( G \left( -\dfrac{7}{4},-\dfrac{49}{16} \right) \)
大問4
石川さんのクラスでは,文化祭の模擬店で販売するためのからあげを \( 300 \) 個作った。このからあげ \( 300 \) 個すべてを,\( 3 \) 個入りと \( 5 \) 個入りに分けて販売することにした。\( 3 \) 個入りは1セット \( 150 \) 円,\( 5 \) 個入りは1セット \( 200 \) 円で販売したところ,模擬店終了時間 \( 30 \) 分前には,\( 5 \) 個入りは売り切れ,\( 3 \) 個入りが \( 10 \) セット残っていた。そこで,この \( 10 \) セットを最初に販売した価格の \( 20 \; % \) 引きで販売したところ,模擬店終了時間までに売り切ることができた。売上金の総額は \( 13500 \) 円であった。
このとき,販売した \( 3 \) 個入りのからあげ,\( 5 \) 個入りのからあげはそれぞれ何セットか,方程式をつくって求めなさい。なお,途中の計算も書くこと。
【解答】
\( 3 \) 個入りのからあげを \( x \) セット,\( 5 \) 個入りのからあげを \( y \) セット販売したとすると,
からあげの個数の関係は \( 3x+5y=300 \)
売上金の関係は \( 150(x-10)+150 \times 0.8 \times 10+200y=13500 \)
と表すことができるので,連立方程式として解くと,
\( \left\{ \begin{array}{}
3x+5y=300 \;\; ・・・ \;\; ➀ \\
150(x-10)+150 \times 0.8 \times 10+200y=13500 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➁を整理すると,
\( 3x+4y=276 \) ・・・ ➁’
➀ \( – \) ➁’
\( y=24 \)
➀に代入すると,
\( 3x+5 \times 24=300 \)
\( 3x=180 \)
\( x=60 \)
よって,販売した
\( 3 \) 個入りのからあげは \( 60 \) セット
\( 5 \) 個入りのからあげは \( 24 \) セット
大問5
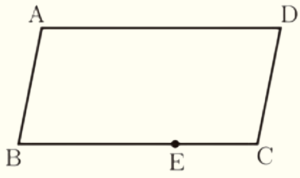
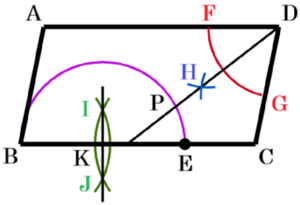
右の図のように,平行四辺形 \( ABCD \) があり,\( ∠ADC=80° \) である。また,辺 \( BC \) 上に点 \( E \) がある。これを用いて,次のの中の条件➀~➂をすべて満たす点 \( P \) を作図しなさい。ただし,作図に用いた線は消さないこと。
➀ 点 \( P \) は,平行四辺形 \( ABCD \) の内部にある。
➁ \( ∠PDC=40° \)
➂ \( ∠BPE=90° \)
【解答】
手順1 点 \( D \) を中心に円弧を描く
(辺 \( AD,CD \) との交点を \( F,G \) とします)
手順2 2点 \( F,G \) を中心に円弧を描く
(交点を \( H \) とします)
手順3 2点 \( D,H \) を通る直線を描く
手順4 2点 \( B,E \) を中心に円弧を描く
(交点を \( I,J \) とします)
手順5 2点 \( I,J \) を通る直線を描く
(辺 \( BC \) との交点を \( K \) とします)
手順6 点 \( K \) を中心に線分 \( BK \) を半径とする
円弧を描く
手順3の直線と手順6の円弧の交点が,求める点 \( P \) になります。
【解説】
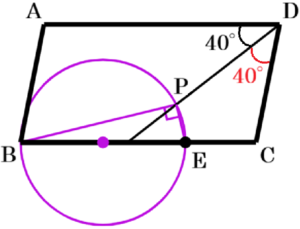
条件➁について,\( ∠ADC=80°,∠PDC=40° \) より,点 \( P \) は \( ∠ADC \) の二等分線上の点であることがわかります。
条件➂について,\( ∠BPE \) を円周角と考えると,
点 \( P \) は線分 \( BE \) を直径とする円周上の点であることがわかります。
線分 \( BE \) を直径とする円の中心は線分 \( BE \) の中点なので,線分 \( BE \) の垂直二等分線を作図することで求めることができます。
大問6
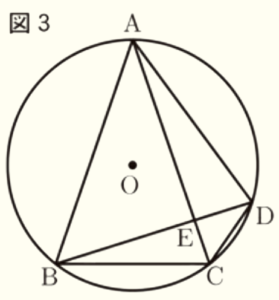
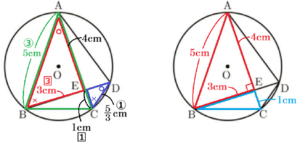
図1~3のように,円 \( O \) の周上に4点 \( A,B,C,D \) があり,\( AB=AC \) とする。また,線分 \( AC \) と \( BD \) の交点を \( E \) とする。
このとき,次の(1)~(3)に答えなさい。
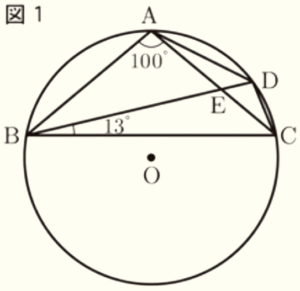
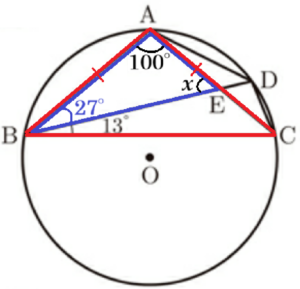
(1) 図1のように,\( ∠BAC=100° \),\( ∠EBC=13° \) のとき,\( ∠AEB \) の大きさを求めなさい。
【解説】
\( △ABC \) は二等辺三角形なので,
\( ∠ABC=\dfrac{180°-100°}{2}=40° \)
\( ∠EBC=13° \) より,
\( ∠ABE=40°-13°=27° \)
\( △ABE \) において,\( ∠AEB=x \) とすると,
\( x=180°-(100°+27°)=53° \)
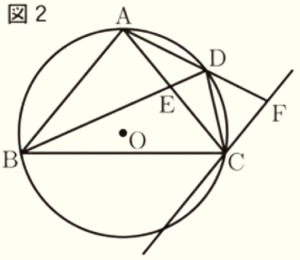
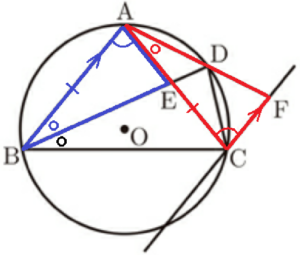
(2) 図2において,\( \stackrel{\huge\frown}{ AD }=\stackrel{\huge\frown}{ DC } \) であり,点 \( C \) を通り,線分 \( AB \) と平行な直線と直線 \( AD \) の交点を \( F \) とする。
このとき,\( △ABE≡△CAF \) であることを証明しなさい。
【解答】
\( △ABE \) と \( △CAF \) において,
仮定より,
\( AB=CA \) ・・・ ➀
\( AB//CF \) より,錯角は等しいので,
\( ∠BAE=∠ACF \) ・・・ ➁
\( \stackrel{\huge\frown}{ AD }=\stackrel{\huge\frown}{ DC } \) より,円周角は等しいので,
\( ∠ABE=∠DBC \) ・・・ ➂
\( \stackrel{\huge\frown}{ DC } \) に対する円周角なので,
\( ∠DBC=∠CAF \) ・・・ ➃
➂➃より,
\( ∠ABE=∠CAF \) ・・・ ➄
➀➁➄より,
1組の辺とその両端の角がそれぞれ等しいので,
\( △ABE≡△CAF \)
(3) 図3において,\( AE=4 \; cm,EC=1 \; cm \),\( CD=\dfrac{5}{3} \; cm \) とする。
このとき,線分 \( BC \) の長さを求めなさい。なお,途中の計算も書くこと。
【解答】
\( △ABC \) は二等辺三角形なので,
\( AB=AC=AE+AC=5 \; cm \)
\( △ABE \) ∽ \( △DCE \) なので,
\( BE:CE=AB:DC \)
\( BE:1=5:\dfrac{5}{3} \)
\( BE=3 \; (cm) \)
\( BE=3 \; cm,AE=4 \; cm,AB=5 \; cm \) なので,
\( △ABE \) は直角三角形であり,\( ∠AEB=90° \)
\( △BCE \) において,三平方の定理より,
\( BC^2=3^2+1^2=10 \)
\( BC=\sqrt{10} \; (cm) \)( \( BC>0 \) より)
大問7
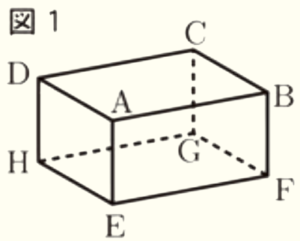
図1,図3,図4の立体 \( ABCD-EFGH \) は,\( AB=2\sqrt{6} \; cm,AD=2\sqrt{3} \; cm,AE=3 \; cm \) の直方体であり,図2は,図1の展開図である。
このとき,次の(1)~(3)に答えなさい。
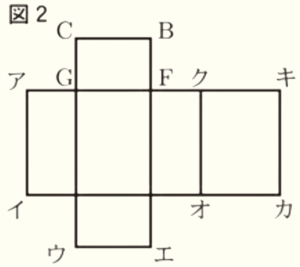
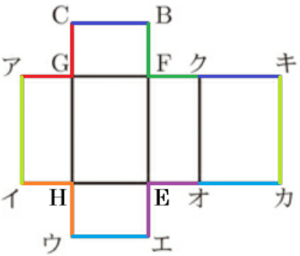
(1) 図2の展開図を組み立てたとき,点 \( C \) と重なる点をア~クからすべて選び,その符号を書きなさい。
【解説】
図2の展開図を組み立てると右の図の同じ色にした辺がくっつくので,点 \( C \) と重なる点は,
アとキになります。
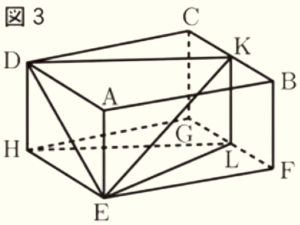
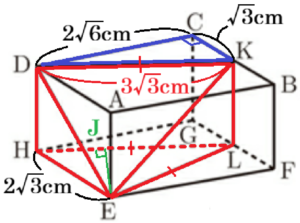
(2) 図3において,辺 \( BC,FG \) の中点をそれぞれ \( K,L \) とする。
このとき,四角錐 \( E-DHLK \) の体積を求めなさい。なお,途中の計算も書くこと。
【解答】
\( 12\sqrt{2} \; cm^3 \)
【解説】
\( △CDK \) において,\( DC=AB=2\sqrt{6} \; cm,CK=\dfrac{1}{2}BC=\sqrt{3} \; cm \) なので,
三平方の定理より,
\( DK^2=(2\sqrt{6})^2+(\sqrt{3})^2=27 \)
\( DK=3\sqrt{3} \; (cm) \)( \( DK>0 \) より)
四角形 \( DHLK \) の面積は,
\( 3 \times 3\sqrt{3}=9\sqrt{3} \; (cm^2) \)
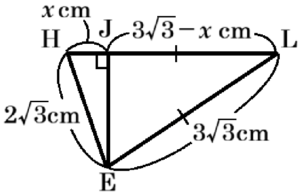
\( △EHL \) において,点 \( E \) から線分 \( HL \) に垂線をひいた交点を \( J \) とし,\( HJ=x \; cm \) とすると,\( EL=HL=DK=3\sqrt{3} \; cm \) なので,
\( (2\sqrt{3})^2-x^2=(3\sqrt{3})^2-(3\sqrt{3}-x)^2 \)
\( 12-x^2=27-(27-6\sqrt{3}x+x^2) \)
\( 6\sqrt{3}x=12 \)
\( x=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \; (cm) \)
となり,
\( EJ^2=(2\sqrt{3})^2-\left( \dfrac{2\sqrt{3}}{3} \right)^2=\dfrac{96}{9} \)
\( EJ=\dfrac{4\sqrt{6}}{3} \; (cm) \)( \( EJ>0 \) より)
四角錐 \( E-DHLK \) の体積は,
\( 9\sqrt{3} \times \dfrac{4\sqrt{6}}{3} \times \dfrac{1}{3}=12\sqrt{2} \; (cm^3) \)
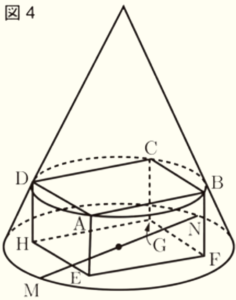
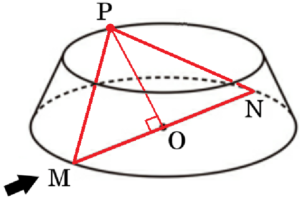
(3) 図4のように,高さ \( 8 \; cm \) の円錐があり,その中に直方体 \( ABCD -EFGH \) が入っている。直方体の頂点のうち,4点 \( A,B,C,D \) は,いずれも円錐の側面上にあり,4点 \( E,F,G,H \) は,いずれも円錐の底面上にある。また,円錐の底面である円の周上に2点 \( M,N \) があり,線分 \( MN \) は円の直径である。
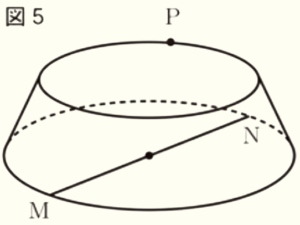
図5は,図4の円錐を4点 \( A,B,C,D \) を通る平面で切断してできた2つの立体のうち,線分 \( MN \) を含むほうであり,切り口の円の周上を動く点を \( P \) とする。
\( △PMN \) の面積が最大となるとき,その面積を求めなさい。なお,途中の計算も書くこと。
【解答】
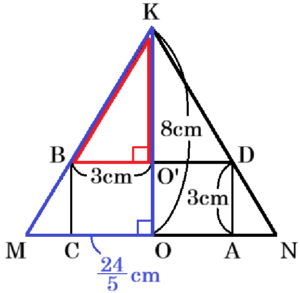
円すいの頂点を \( K \) ,底面の円の中心を \( O \),
切り口の円の中心を \( O’ \) とすると,
\( △KBO’ \) ∽ \( △KMO \) であり,
切り口の円の直径は四角形 \( ABCD \) の対角線になるので,
\( KO’:KO=O’B:OM \)
\( 5:8=3:OM \)
\( OM=\dfrac{24}{5} \; (cm) \)
ここから,
\( MN=2OM=\dfrac{48}{5} \; (cm) \)
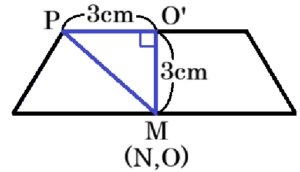
\( △PMN \) の面積が最大になるのは,
\( OP⊥MN \) になるときであり,
\( ∠OO’P=90° \) なので,
\( OP^2=3^2+3^2=18 \)
\( OP=3\sqrt{2} \; (cm) \)( \( OP>0 \) より)
よって,\( △PMN \) の面積は,
\( △PMN=\dfrac{48}{5} \times 3\sqrt{2} \times \dfrac{1}{2}=\dfrac{72\sqrt{2}}{5} \; (cm^2) \)
【解答】
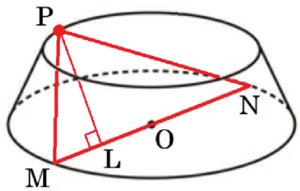
● \( △PMN \) の面積が最大になるのは,\( OP⊥MN \) になるときである理由
線分 \( MN \) を底辺とすると,点 \( P \) から線分 \( MN \) にひいた垂線の長さが高さになります。
点 \( P \) がどの位置にあっても,線分 \( MN \) は固定なので,高さ(垂線の長さ)の値が最大のとき,
\( △PMN \) の面積も最大になります。
\( OP⊥MN \) になる位置に点 \( P \) があるとき,\( O’P=3 \; cm \) になります。
これ以外の位置に点 \( P \) があるとき,
点 \( P \) から線分 \( MN \) に垂線をひいた交点を \( L \).
点 \( L \) から切り口の面に垂線をひいた交点を \( L’ \)
とすると,線分 \( L’P \) は \( O’P \) より短くなりす。
線分 \( L’P=x \; cm \) とするとき,
\( OP=\sqrt{3^2+3^2} cm \)
\( LP=\sqrt{x^2+3^2} cm \)
であり,\( x<3 \) より \( OP>LP \) なので,
\( OP⊥MN \) になるときに \( △PMN \) の面積が最大になります。