大問1
(ア) \( -1-(-7) \)
1 \( -8 \) 2 \( -6 \) 3 \( 6 \) 4 \( 8 \)
【解説】
\( =-1+7 \)
\( =6 \)
(イ) \( -\dfrac{3}{7}+\dfrac{1}{2} \)
1 \( -\dfrac{13}{14} \) 2 \( -\dfrac{1}{14} \) 3 \( \dfrac{1}{14} \) 4 \( \dfrac{13}{14} \)
【解答】
3 \( \dfrac{1}{14} \)
【解説】
\( =\dfrac{-3 \times 2+1 \times 7}{14} \)
\( =\dfrac{1}{14} \)
(ウ) \( 12ab^2 \times 6a \div (-3b) \)
1 \( -24a^2b \) 2 \( -24ab^2 \) 3 \( 24a^2b \) 4 \( 24ab^2 \)
【解説】
\( =\dfrac{12ab^2 \times 6a}{-3b} \)
\( =-24a^2b \)
(エ) \( \dfrac{3x+2y}{7}-\dfrac{2x-y}{5} \)
1 \( \dfrac{x-17y}{35} \) 2 \( \dfrac{x-3y}{35} \) 3 \( \dfrac{x+3y}{35} \) 4 \( \dfrac{x+17y}{35} \)
【解答】
4 \( \dfrac{x+17y}{35} \)
【解説】
\( =\dfrac{5(3x+2y)-7(2x-y)}{35} \)
\( =\dfrac{15x+10y-14x+7y}{35} \)
\( =\dfrac{x+17y}{35} \)
(オ) \( (\sqrt{6}+5)^2-5(\sqrt{6}+5) \)
1 \( 6-5\sqrt{6} \) 2 \( 6+5\sqrt{6} \) 3 \( 6+10\sqrt{6} \) 4 \( 6+15\sqrt{6} \)
【解説】
\( \sqrt{6}+5=A \) とすると,
与式 \( =A^2-5A \)
\( =A(A-5) \)
\( =(\sqrt{6}+5)(\sqrt{6}+5-5) \)
\( =(\sqrt{6}+5) \times \sqrt{6} \)
\( =6+5\sqrt{6} \)
大問2
次の問いに対する答えとして正しいものを,それぞれあとの1~4の中から1つずつ選び,その番号を答えなさい。
(ア) \( (x-5)(x+3)-2x+10 \) を因数分解しなさい。
1 \( (x-3)(x+3) \) 2 \( (x-5)(x+1) \) 3 \( (x-5)(x+5) \) 4 \( (x+5)(x-1) \)
【解説】
\( (x-5)(x+3)-2x+10=x^2-2x-15-2x+10 \)
\( =x^2-4x-5 \)
\( =(x-5)(x+1) \)
(イ) 2次方程式 \( 7x^2+2x-1=0 \) を解きなさい。
1 \( x=\dfrac{-1±2\sqrt{2}}{7} \) 2 \( x=\dfrac{-1±4\sqrt{2}}{7} \) 3 \( x=\dfrac{1±2\sqrt{2}}{7} \) 4 \( x=\dfrac{1±4\sqrt{2}}{7} \)
【解答】
1 \( x=\dfrac{-1±2\sqrt{2}}{7} \)
【解説】
この方程式を \( ax^2+bx+c=0 \) と考えると,\( a=7,b=2,c=-1 \) なので,
\( x=\dfrac{-2±\sqrt{2^2-4 \times 7 \times (-1)}}{2 \times 7} \)
\( =\dfrac{-2±\sqrt{32}}{14} \)
\( =\dfrac{-1±2\sqrt{2}}{7} \)
(ウ) 関数 \( y=-2x^2 \) について,\( x \) の値が \( -3 \) から \( -1 \) まで増加するときの変化の割合を求めなさい。
1 \( -8 \) 2 \( -4 \) 3 \( 4 \) 4 \( 8 \)
【解説】
\( x=-3 \) のときの \( y \) の値は,\( y=-2 \times (-3^2)=-18 \)
\( x=-1 \) のときの \( y \) の値は,\( y=-2 \times (-1^2)=-2 \)
なので,
変化の割合 \( =\dfrac{-2-(-18)}{-1-(-3)}=8 \)
(エ) 十の位の数が \( 4 \) である3桁の自然数がある。この自然数の百の位の数と一の位の数の和は10であり,百の位の数と一の位の数を入れかえた数はこの自然数より \( 396 \) 大きい。
このとき,この自然数の一の位の数を求めなさい。
1 \( 6 \) 2 \( 7 \) 3 \( 8 \) 4 \( 9 \)
【解説】
もとの自然数の百の位の数を \( a \),一の位の数を \( b \) とすると,
もとの自然数は \( 100a+40+b \),
百の位の数と一の位の数を入れかえた数は \( 100b+40+a \)
と表すことができるので,
\( (100b+40+a)-(100a+40+b)=396 \)
\( 99b-99a=396 \)
\( b-a=4 \) ・・・ ➀
百の位の数と一の位の数の和は10なので,\( a+b=10 \) ・・・ ➁
➀➁を連立方程式として解くと,\( a=3,b=7 \)
よって,もとの自然数の一の位の数は \( 7 \)
(オ) \( \dfrac{3780}{n} \) が自然数の平方となるような,最も小さい自然数 \( n \) の値を求めなさい。
1 \( n=35 \) 2 \( n=70 \) 3 \( n=105 \) 4 \( n=210 \)
【解説】
\( 3780 \) を素因数分解すると,\( 2^2 \times 3^3 \times 5 \times 7 \) なので,
\( \dfrac{3780}{n}=\dfrac{2^2 \times 3^3 \times 5 \times 7}{n} \)
これが,自然数の平方となる条件は,
・約分ができる
・約分した結果が \( m^2 \) (\( m \) は自然数) の形になる
ことなので,
これを満たす \( n \) のうち,もっとも小さいものは,\( n=3 \times 5 \times 7=105 \)
\( \dfrac{3780}{n}=\dfrac{2^2 \times 3^3 \times 5 \times 7}{3 \times 5 \times 7}=2^2 \times 3^2=6^2 \)
大問3
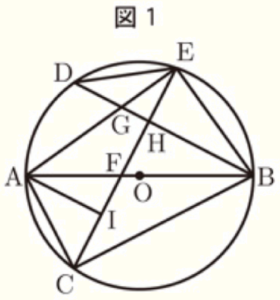
(ア) 右の図1のように,線分 \( AB \) を直径とする円 \( O \) の周上に,2点 \( A,B \) とは異なる点 \( C \) を,\( AC<BC \) となるようにとり,点 \( C \) を含まない弧 \( AB \) 上に点 \( D \) を,\( ∠ABC=∠ABD \) となるようにとる。
また,点 \( A \) を含まない弧 \( BD \) 上に,2点 \( B,D \) とは異なる点 \( E \) をとり,線分 \( AB \) と線分 \( CE \) との交点を \( F \),線分 \( AE \) と線分 \( BD \) との交点を \( G \),線分 \( BD \) と線分 \( CE \) との交点を \( H \) とする。
さらに,線分 \( CE \) 上に点 \( I \) を,\( DB//AI \) となるようにとる。
このとき,次の(ⅰ),(ⅱ)に答えなさい。
(ⅰ) 三角形 \( AIF \) と三角形 \( EHG \) が相似であることを次のように証明した。 (a) ~ (c) に最も適するものを,それぞれ選択肢の1~4の中から1つずつ選び,その番号を答えなさい。
[証明]
\( △AIF \) と \( △EHG \) において,
まず,\( DB//AI \) より,平行線の同位角は等しいから,
(a)
よって,\( ∠AIF=∠EHG \) ・・・ ➀
次に,仮定より,
\( ∠ABC=∠ABD \) ・・・ ➁
また,弧 \( AC \) に対する円周角は等しいから,
\( ∠ABC=∠AEC \) ・・・ ③
さらに,\( DB//AI \) より,平行線の錯角は等しい
から,
(b) ・・・ ➃
➁,③,➃ より,\( ∠AEC=∠BAI \)
よって,\( ∠FAI=∠GEH \) ・・・ ➄
➀,➄ より, (c) から,
\( △AIF \) ∽ \( △EHG \)
(a),(b) の選択肢
1. \( ∠ABD=∠BAI \)
2. \( ∠AIE=∠BHC \)
3. \( ∠AIE=∠DHE \)
4. \( ∠EAI=∠EGB \)
(c) の選択肢
1. 1組の辺とその両端の角がそれぞれ等しい
2. 2組の辺の比とその間の角がそれぞれ等しい
3. 3組の辺の比がすべて等しい
4. 2組の角がそれぞれ等しい
【解答】
(a) ・・・ 3. \( ∠AIE=∠DHE \)
(b) ・・・ 1. \( ∠ABD=∠BAI \)
(c) ・・・ 4. 2組の角がそれぞれ等しい
(ⅱ) 次の の中の「あ」「い」にあてはまる数字をそれぞれ0~9の中から1つずつ選び,その数字を答えなさい。
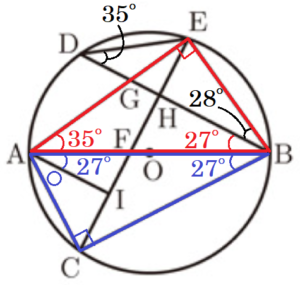
\( ∠BDE=35°,∠DBE=28° \) のとき,\( ∠CAI \) の大きさは あ い ° である。
【解説】
\( △ABE \) において,
直径 \( AB \) に対する円周角なので,\( ∠AEB=90° \)
弧 \( BE \) に対する円周角なので,\( ∠BAE=∠BDE=35° \)
仮定より,\( ∠DBE=28° \)
ここから,\( ∠ABD=180°-(90°+35°+28°)=27° \)
\( △ABC \) において,
仮定より,\( ∠ABC=∠ABD=27° \)
\( DB//AI \) より,錯角は等しいので,\( ∠BAI=∠ABD=27° \)
直径 \( AB \) に対する円周角なので,\( ∠ACB=90° \)
ここから,\( ∠CAI=180°-(90°+27°+27°)=36° \)
(イ) ある中学校で1学年から3学年まであわせて10クラスの生徒が集まり生徒総会を開催した。生徒総会では生徒会から3つの議案X,Y,Zが提出され,それぞれの議案について採決を行った。
右の資料1は議案Xに賛成した人数を,資料2は議案Yに賛成した人数を,それぞれクラスごとに記録したものである。資料3は議案Zに賛成した人数をクラスごとに記録し,その記録の平均値,中央値,四分位範囲をまとめたものである。
このとき,次の(ⅰ),(ⅱ) に答えなさい。
(ⅰ) 資料1の記録を箱ひげ図に表したものとして最も適するものを次の1~4の中から1つ選び,その番号を答えなさい。
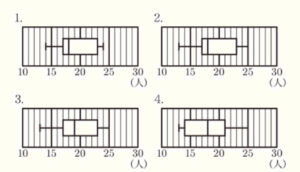
【解説】
資料1の記録を賛成した人が少ない順に並べ替えると,
\( 13,14,17,17,17,19,21,23,24,25 \)
全部で10クラスの記録なので,
第一四分位数は,少ない方から3番目のクラスの値になるので,\( 17 \)(人)
中央値は,少ない方から5番目と6番目のクラスの値の平均値になるので,\( \dfrac{17+19}{2}=18 \)(人)
第三四分位数は,多い方から3番目のクラスの値になるので,\( 23 \)(人)
また,最小値は \( 13 \) 人,最大値は \( 25 \) 人
となるので,これらをすべて満たしている箱ひげ図は 2 になります。
(ⅱ) 資料2と資料3から読み取れることがらを,次のA~Dの中からすべて選んだときの組み合わせとして最も適するものをあとの1~6の中から1つ選び,その番号を答えなさい。
A. 議案Yに賛成した人数の最頻値は20人である。
B. 賛成した人数の合計は,議案Zより議案Yの方が多い。
C. 賛成した人数の中央値は,議案Zより議案Yの方が大きい。
D. 賛成した人数の四分位範囲は,議案Zより議案Yの方が小さい。
1. A,B 2. A,C 3. B,D
4. C,D 5. A,B,C 6. A,C,D
【解説】
A.資料2の中で,賛成した人数が20人であったクラスは3クラスで最も多いので
正しい。
B.議案Yに賛成した人数の合計は,
\( 20+26+19+27+25+24+20+15+24+20=220 \)(人)
議案Zに賛成した人数の合計は, \( 23 \times 10=230 \)(人)
なので,間違っている。
C.資料2の記録を賛成した人が少ない順に並べ替えると,
\( 15,19,20,20,20,24,24,25,26,27 \)
議案Yに賛成した人数の中央値は,少ない方から5番目と6番目のクラスの値の平均値なので,
\( \dfrac{20+24}{2}=22 \)(人)
よって正しい。
D.資料2より第一四分位数は \( 20 \)人,第三四分位数は \( 25 \)人であり,
議案Yに賛成した人数の四分位範囲は,\( 25-20=5 \)(人)なので,
正しい。
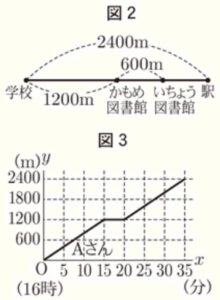
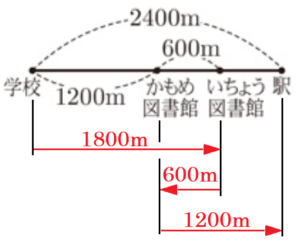
(ウ) 学校から駅までの道のりは \( 2400 \; m \) であり,その途中にかもめ図書館といちょう図書館がある。AさんとBさんは \( 16 \) 時に学校を出発し,それぞれが図書館に立ち寄ってから駅まで移動する中で一度すれ違ったが,駅には同時に到着した。
Aさんは,かもめ図書館に \( 5 \) 分間立ち寄って本を借り,駅まで移動した。Bさんは,いちょう図書館に \( 15 \) 分間立ち寄って借りたい本を探したが見つからなかったため道を引き返し,かもめ図書館に \( 5 \) 分間立ち寄って本を借り,駅まで移動した。
次の図2は,学校,かもめ図書館,いちょう図書館,駅の間の道のりを示したものである。図3は,\( 16 \) 時に学校を出発してから \( x \) 分後の学校からの道のりを \( y \; m \) として,Aさんが駅に到着するまでの \( x \) と \( y \) の関係をグラフに表したものであり,\( O \) は原点である。
このとき,AさんとBさんがすれ違った時間帯として最も適するものをあとの1~6の中から1つ選び,その番号を答えなさい。ただし,AさんとBさんの,それぞれの移動中の速さは常に一定であり,図書館での移動は考えないものとする。
1. \( 16 \) 時 \( 19 \) 分から \( 16 \) 時 \( 21 \) 分までの間 2. \( 16 \) 時 \( 21 \) 分から \( 16 \) 時 \( 23 \) 分までの間
3. \( 16 \) 時 \( 23 \) 分から \( 16 \) 時 \( 25 \) 分までの間 4. \( 16 \) 時 \( 25 \) 分から \( 16 \) 時 \( 27 \) 分までの間
5. \( 16 \) 時 \( 27 \) 分から \( 16 \) 時 \( 29 \) 分までの間 6. \( 16 \) 時 \( 29 \) 分から \( 16 \) 時 \( 31 \) 分までの間
【解答】
3. \( 16 \) 時 \( 23 \) 分から \( 16 \) 時 \( 25 \) 分までの間
【解説】
Bさんが移動した道のりは,全部で \( 3600 \; m \)で,
移動にかかった時間は \( 15 \) 分なので,
Bさんが移動した速さは,\( \dfrac{3600}{15}=240 \) より,
毎分 \( 240 \; m \)
ここから,図3にBさんが移動した状態を表すグラフを書き加えると,下の図のようになります。
下のグラフから,Bさんが
いちょう図書館を出発するのは,\( x=22.5 \) のとき,
かもめ図書館に到着するのは,\( x=25 \) のとき
なので,あてはまるのは 3
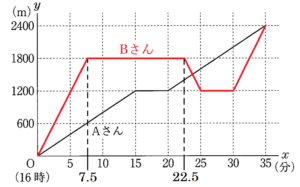
(エ) 次の の中の う , え にあてはまる数字をそれぞれ0~9の中から1つずつ選び,その数字を答えなさい。
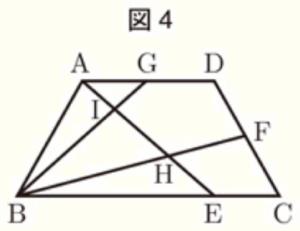
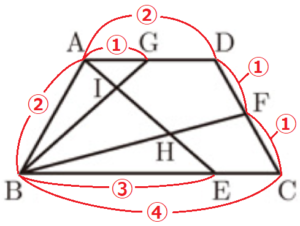
右の図4において,四角形 \( ABCD \) は \( AB=CD=DA \) ,
\( AB:BC=1:2 \) の台形である。
また,点 \( E \) は辺 \( BC \) 上の点で \( BE:EC=3:1 \) であり,
2点 \( F,G \) はそれぞれ辺 \( CD,DA \) の中点である。
さらに,線分 \( AE \) と線分 \( BF \) との交点を \( H \),線分 \( AE \) と
線分 \( BG \) との交点を \( I \) とする。
三角形 \( BHI \) の面積を \( S \),四角形 \( CFHE \) の面積を \( T \) と
するとき,\( S \) と \( T \) の比を最も簡単な整数の比で表すと,
\( S:T= \) う : え である。
【解説】
問題で与えられた条件から,線分 \( AG \) の長さを ➀ とするとき,
それぞれの線分の長さは,右の図のとおりになります。
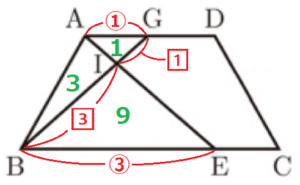
\( △AIG \) ∽ \( △EIB \),\( AG:EB=1:3 \) より,
\( △AIG:△EIB=1:9 \) なので,
\( △AIG= \)【1】とすると,\( △EIB= \)【9】
\( △AIG \) と \( △AIB \) は,高さが共通なので,
\( △AIG:△AIB=GI:BI=1:3 \)
ここから,\( △AIB= \)【3】
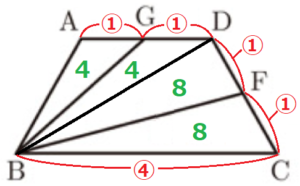
\( △AGB \) と \( △DGB \) は,高さが共通なので,
\( △AGB:△DGB=AG:GD=1:1 \)
\( △AGB= \)【3】\( + \)【1】\( = \)【4】より,
\( △DGB=△AGB= \)【4】
\( △ADB \) と \( △BCD \) は,高さが共通なので,
\( △ADB:△BCD=AD:BC=1:2 \)
\( △ADB= \)【8】より,\( △BCD=2△ADB= \)【16】
\( △BDF \) と \( △BCF \) は,高さが共通なので,
\( △BDF:△BCF=CF:DF=1:1 \)
\( △BCD= \)【16】より,\( △BCF=\dfrac{1}{2}△BCD= \)【8】
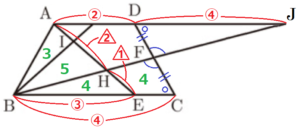
線分 \( BF,AD \) の延長線の交点を \( J \) とすると,
\( △BCF≡△JDF \) なので,\( BC=JD= \) ➃
\( △BEH \) ∽ \( △JAH \),\( BE:JA=1:2 \) より,
\( EH:AH=1:2 \)
\( △BEH \) と \( △ABH \) は,高さが共通なので,\( △BEH:△ABH=EH:AH=1:2 \)
\( △ABE= \)【12】より,\( △BEH=\dfrac{1}{3}△ABE= \)【4】
\( △BHI=△ABE-(△AIB+△BEH)= \)【12】\( -( \)【3】\( + \)【4】\( )= \)【5】
四角形 \( CFHE=△BCF-△BEH= \)【8】\( – \)【4】\( = \)【4】
よって,\( △BHI: \) 四角形 \( CFHE=5:4 \)
大問4
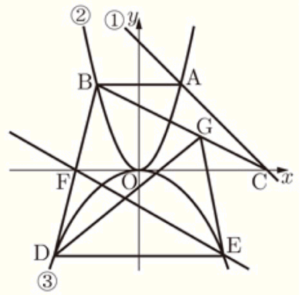
右の図において,直線 ➀ は関数 \( y=-x+9 \) のグラフであり,曲線 ➁ は関数 \( y=ax^2 \) のグラフ,
曲線 ➂ は関数 \( y=-\dfrac{1}{6}x^2 \) のグラフである。
点 \( A \) は直線 ➀ と曲線 ➁ との交点で,その \( x \) 座標は \( 3 \) である。点 \( B \) は曲線 ➁ 上の点で,線分 \( AB \) は \( x \) 軸に平行である。点 \( C \) は直線 ➀ と \( x \) 軸との交点である。
また,2点 \( D,E \) は曲線 ➂ 上の点で,点 \( D \) の \( x \) 座標は \( -6 \) であり,線分 \( DE \) は \( x \) 軸に平行である。
さらに,点 \( F \) は線分 \( BD \) と \( x \) 軸との交点である。
原点を \( O \) とするとき,次の問いに答えなさい。
(ア) 曲線 ➁ の式 \( y=ax^2 \) の \( a \) の値として正しいものを次の1~6の中から1つ選び,その番号を答えなさい。
1. \( a=\dfrac{1}{4} \) 2. \( a=\dfrac{1}{3} \) 3. \( a=\dfrac{2}{5} \)
4. \( a=\dfrac{1}{2} \) 5. \( a=\dfrac{2}{3} \) 6. \( a=\dfrac{3}{4} \)
【解答】
5. \( a=\dfrac{2}{3} \)
【解説】
点 \( A \) は \( y=-x+9 \) 上の点で,
\( x \) 座標は \( 3 \) なので,\( y \) 座標の値は
\( y=-3+9=6 \)
よって,
\( y=ax^2 \) に \( x=3,y=6 \) を代入すると,
\( 6=a \times 3^2 \)
\( a=\dfrac{2}{3} \)
(イ) 直線 \( EF \) の式を \( y=mx+n \) とするときの (ⅰ)\( m \) の値 と,(ⅱ)\( n \) の値 として正しいものを,それぞれ次の1~6の中から1つずつ選び,その番号を答えなさい。
(ⅰ) \( m \) の値
1. \( m=-\dfrac{5}{6} \) 2. \( m=-\dfrac{5}{7} \) 3. \( m=-\dfrac{2}{3} \)
4. \( m=-\dfrac{4}{7} \) 5. \( m=-\dfrac{1}{3} \) 6. \( m=-\dfrac{1}{6} \)
(ⅱ) \( n \) の値
1. \( n=-\dfrac{18}{7} \) 2. \( n=-\dfrac{5}{2} \) 3. \( n=-\dfrac{7}{3} \)
4. \( n=-\dfrac{13}{6} \) 5. \( n=-\dfrac{15}{7} \) 6. \( n=-2 \)
【解答】
(ⅰ)・・・ 4. \( m=-\dfrac{4}{7} \)
(ⅱ)・・・ 1. \( n=-\dfrac{18}{7} \)
【解説】
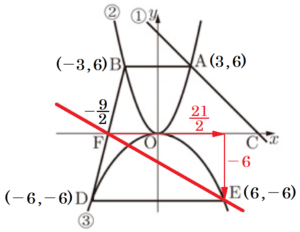
点 \( B \) の \( y \) 座標は,点 \( A \) の \( y \) 座標と等しいので,\( B(-3,6) \)
点 \( D \) は \( y=-\dfrac{1}{6}x^2 \) 上の点で,
\( x \) 座標は \( -6 \) なので,\( y \) 座標の値は
\( y=-\dfrac{1}{6} \times (-6)^2=-6 \)
であり,\( D(-6,-6) \) になります。
\( B(-3,6),D(-6,-6), \)点 \( F \) の \( y \) 座標は \( 0 \) より,点 \( F \) は線分 \( BD \) の中点になっています。
ここから,点 \( F \) の \( x \) 座標は,
\( \dfrac{-3+(-6)}{2}=-\dfrac{9}{2} \)
よって,\( F \left( -\dfrac{9}{2},0 \right) \)
点 \( E \) の \( y \) 座標は,点 \( D \) の \( y \) 座標と等しいので,\( E(6,-6) \)
直線 \( EF \) の傾き \( m \) は,
\( m=\dfrac{-6-0}{6-\left( -\dfrac{9}{2} \right)}=-\dfrac{4}{7} \)
\( y=-\dfrac{4}{7}x+n \) に \( x=6,y=-6 \) を代入すると,
\( -6=-\dfrac{4}{7} \times 6+n \)
\( n=-\dfrac{18}{7} \)
(ウ) 次の の中の「お」「か」「き」「く」にあてはまる数字をそれぞれ0~9の中から1つずつ選び,その数字を答えなさい。
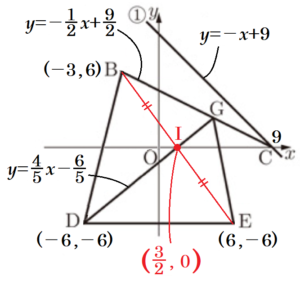
線分 \( BC \) 上に点 \( G \) を,三角形 \( BDG \) と三角形 \( DEG \) の面積が等しくなるようにとる。このときの,点 \( G \) の \( x \) 座標は \( \dfrac{\fbox{ おか }}{\fbox{ きく }} \) である。
【解答】
\( \dfrac{57}{13} \)
【解説】
\( △BDG \) と \( △DEG \) は,辺 \( DG \) が共通で,
面積が等しいので,線分 \( BE \) と辺 \( DG \) は,
線分 \( BE \) の中点で交わります。
(詳細は別途解説あり)
線分 \( BE \) の中点を点 \( I \) とすると,
\( B(-3,6),E(6,-6) \) より,
\( I \) の \( x \) 座標は,\( \dfrac{-3+6}{2}=\dfrac{3}{2} \)
\( y \) 座標は,\( \dfrac{6+(-6)}{2}=0 \)
直線 \( DG \) は,\( D(-6,-6),I\left(\dfrac{3}{2},0 \right) \) を通るので,
傾き \( =\dfrac{0-(-6)}{\dfrac{3}{2}-(-6)}=\dfrac{4}{5} \)
線分 \( DG \) の式を \( y=\dfrac{4}{5}x+b \) とし,\( x=-6,y=-6 \) とすると,
\( -6=\dfrac{4}{5} \times (-6)+b \)
\( b=-\dfrac{6}{5} \)
点 \( C \) は,\( y=-x+9 \) と \( x \) 軸の交点なので,\( C(9,0) \) であり,
直線 \( BC \) は,\( B(-3,6),C(9,0) \) を通るので,
傾き \( =\dfrac{0-6}{9-(-3)}=-\dfrac{1}{2} \)
直線 \( BC \) の式を \( y=-\dfrac{1}{2}x+b \) とし,\( x=9,y=0 \) とすると,
\( 0=-\dfrac{1}{2} \times 9+b \)
\( b=\dfrac{9}{2} \)
点 \( G \) は,直線 \( DG \) と直線 \( BC \) の交点なので,
\( y=\dfrac{4}{5}x-\dfrac{6}{5} \) と \( y=-\dfrac{1}{2}x+\dfrac{9}{2} \) を連立方程式として解くと,
\( x=\dfrac{57}{13} \)
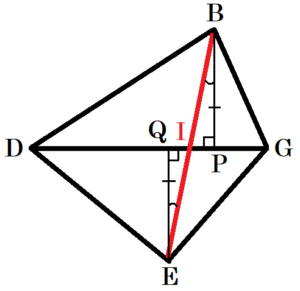
なぜ「BEの中点で交わる」っていえるの?
\( △BDG \) と \( △DEG \) は,辺 \( DG \) が共通で,面積が等しいので,高さは等しくなります。
点 \( B,E \) から辺 \( DG \) に垂線をひき,
交点をそれぞれ \( P,Q \),
線分 \(BE\) と辺 \( DG \) の交点を \( I \)
とすると,
\( △BIP \) と \( △EIQ \) において,
線分 \( BP \) は \( △BDG \) の高さ,
線分 \( EQ \) は \( △DEG \) の高さにあたるので,
\( BP=EQ \) ・・・ ➀
\( BP⊥DG,EQ⊥DG \) より,
\( ∠BPI=∠EQI \) ・・・ ➁
\( BP//EQ \) なので,錯角は等しく,
\( ∠IBP=∠IEQ \) ・・・ ➂
➀➁➂より,
1組の辺とその両端の角がそれぞれ等しいので,
\( △BIP≡△EIQ \)
対応する辺の長さは等しいので,\( BI=EI \)
よって,線分 \( BE \) と辺 \( DG \) は,線分 \( BE \) の中点で交わります。
大問5
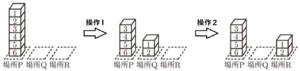
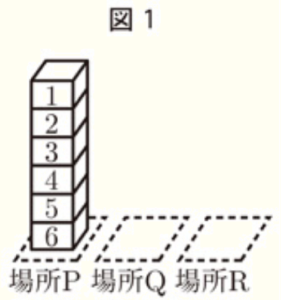
右の図1のように,場所P,場所Q,場所Rがあり,場所Pには,\( 1,2,3,4,5,6 \) の数が1つずつ書かれた6個の直方体のブロックが,書かれた数の大きいものから順に,下から上に向かって積まれている。
大, 小2つのさいころを同時に1回投げ,大きいさいころの出た目の数を \( a \),小さいさいころの出た目の数を \( b \) とする。出た目の数によって,次の【操作1】,【操作2】を順に行い,場所P,場所Q,場所Rの3か所にあるブロックの個数について考える。
【操作1】 \( a \) と同じ数の書かれたブロックと,その上に積まれているすべてのブロックを,順番を変えずに
場所Qへ移動する。
【操作2】 \( b \) と同じ数の書かれたブロックと,その上に積まれているすべてのブロックを,\( b \) と同じ数の
書かれたブロックが場所P,場所Qのどちらにある場合も場所Rへ移動する。
例
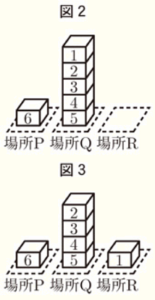
大きいさいころの出た目の数が \( 5 \),小さいさいころの出た目の数が \( 1 \) のとき,\( a=5,b=1 \) だから,
【操作1】 図1の,\( 5 \) が書かれたブロックと,その上に積まれている
すべてのブロックを,順番を変えずに場所Qへ移動するの
で,図2のようになる。
【操作2】 図2の,\( 1 \) が書かれたブロックを,場所Rへ移動するの
で,図3のようになる。
この結果,3か所にあるブロックの個数は,場所Pに1個,場所Qに4個,場所Rに1個となる。
いま,図1の状態で,大,小2つのさいころを同時に1回投げるとき,次の問いに答えなさい。ただし,大,小2つのさいころはともに,\( 1 \) から \( 6 \) までのどの目が出ることも同様に確からしいものとする。
(ア) 次の の中の「け」「こ」「さ」にあてはまる数字をそれぞれ0~9の中から1つずつ選び,その数字を答えなさい。
ブロックの個数が3か所とも同じになる確率は \( \dfrac{\fbox{ け }}{\fbox{ こさ }} \) である。
【解説】
ブロックの個数が3か所とも同じになるのは,それぞれ2個ずつになるときなので,
あてはまる組み合わせは,\( a=2,b=4 \) または \( a=4,b=2 \) の2通り。
すべての組み合わせは36通りなので,求める確率は \( \dfrac{1}{18} \)
\( a=2,b=4 \) のとき
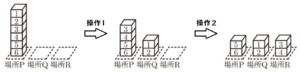
\( a=4,b=2 \) のとき

(イ) 次の の中の「し」「す」にあてはまる数字をそれぞれ0~9の中から1つずつ選び,その数字を答えなさい。
3か所のうち,少なくとも1か所のブロックの個数が0個になる確率は \( \dfrac{\fbox{ し }}{\fbox{ す }} \) である。
【解説】
大きいさいころの出た目の数に注目すると,
● \( a=6 \) の場合
場所Pにあるブロックすべてを場所Qに移動させるので,場所Pにあるブロックの個数は0個になります。
場所Qから場所Pに戻すことはないので,この場合は,小さいさいころの出た目の数はどれでもいいことになります。
例:\( a=6,b=2 \) のとき
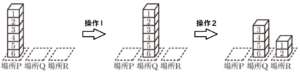
● \( a=1,2,3,4,5 \) の場合
大きいさいころの出た目の数 \( a \) と同じ個数のブロックを場所Pから場所Qに移動させるので,
小さいさいころの出た目の数 \( b \) の値が \( b=a \) のとき,
【操作1】で場所Pから場所Qに移動させたブロックをすべて場所Rに移動させることになり,
場所Qにあるブロックの個数が0個になります。
例1:\( a=2,b=2 \) のとき
小さいさいころの出た目の数 \( b \) の値が \( b=6 \) のとき,
【操作1】で移動させなかったブロックをすべて場所Rに移動させることになり,
場所Pにあるブロックの個数が0個になります。
例2:\( a=2,b=6 \) のとき
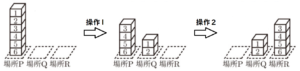
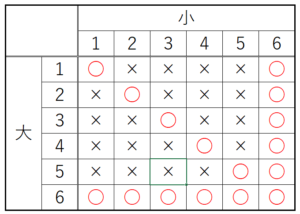
これらを踏まえて,大きいさいころと小さいさいころの出た目の数の組み合わせを表に書き出し,
ブロックの数が0個になる場所があるところに ○ をつけてみると,
0個になる場所がある組み合わせは16通り,
すべての組み合わせは36通り
なので,求める確率は \( \dfrac{16}{36}=\dfrac{4}{9} \)
大問6
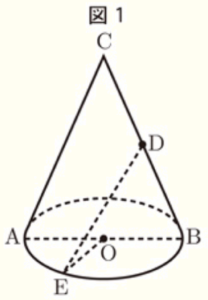
右の図1は,線分 \( AB \) を直径とする円 \( O \) を底面とし,線分 \( AC \) を母線とする円すいである。
また,点 \( D \) は線分 \( BC \) の中点である。
さらに,点 \( E \) は円 \( O \) の周上の点である。
\( AB=8 \; cm,AC=10 \; cm,∠AOE=60° \) のとき,次の問いに答えなさい。ただし,円周率は \( \pi{} \) とする。
(ア) この円すいの表面積として正しいものを次の1~6の中から1つ選び,その番号を答えなさい。
1, \( 24\pi{} \; cm^2 \) 2. \( 28\pi{} \; cm^2 \)
3. \( 40\pi{} \; cm^2 \) 4. \( 48\pi{} \; cm^2 \)
5. \( 56\pi{} \; cm^2 \) 6. \( 84\pi{} \; cm^2 \)
【解答】
5. \( 56\pi{} \; cm^2 \)
【解説】
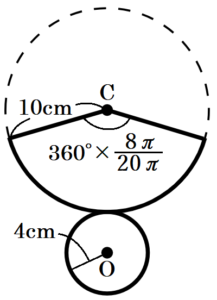
このおうぎ形を展開すると,
半径 \( 10 \; cm \) のおうぎ形と半径 \( 4 \; cm \) の円ができます。
半径 \( 10 \; cm \) のおうぎ形の面積は,
\( \pi{} \times 10^2 \times \dfrac{8\pi{}}{20\pi{}}=40\pi{} \; (cm^2) \)
半径 \( 4 \; cm \) の円の面積は,
\( \pi{} \times 4^2=16\pi{} \; (cm^2) \)
よって,この円すいの表面積は,\( 40\pi{}+16\pi{}=56\pi{} \; (cm^2) \)
(イ) この円すいにおいて,2点 \( D,E \) 間の距離として正しいものを次の1~6の中から1つ選び,その番号を答えなさい。
1, \( \sqrt{43} \; cm \) 2. \( 7 \; cm \)
3. \( 5\sqrt{2} \; cm \) 4. \( \sqrt{57} \; cm \)
5. \( 3\sqrt{7} \; cm \) 6. \( 8 \; cm \)
【解説】
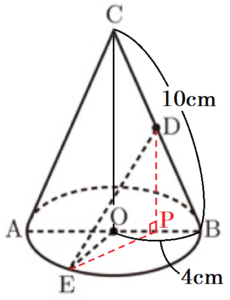
点 \( D \) から線分 \( AB \) に垂線をひき,交点を点 \( P \) とすると,
\( △DPE \) は直角三角形になるので,線分 \( DP,EP \) の長さがわかれば,
三平方の定理を使って線分 \( DE \) の長さを求めることができます。
点 \( D \) は線分 \( BC \) の中点なので,
\( △COB \) ∽ \( △DPB \),相似比は \( 2:1 \)
になっています。
\( OB=\dfrac{1}{2}AB=4 \; cm,BC=AC=10 \; cm \) なので,
三平方の定理より,
\( CO^2=10^2-4^2=84 \)
\( CO=2\sqrt{21} \; (cm) \) (\( CO>0 \) より)
\( DP=\dfrac{1}{2}CO=\sqrt{21} \; (cm) \)
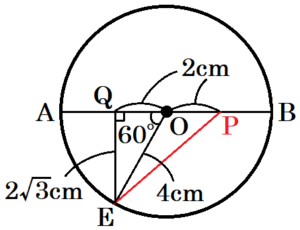
点 \( E \) から線分 \( AB \) に垂線をひき,交点を点 \( Q \) とすると,
\( △OQE \) は \( 30°,60°,90° \) の直角三角形になるので,
\( EQ=\dfrac{ \sqrt{3}}{2}OE=2\sqrt{3} \; (cm) \)
また,\( OQ=\dfrac{1}{2}OE=2 \; (cm),OP=\dfrac{1}{2}OB=2 \; (cm) \) より,
\( PQ=4 \; cm \) なので,三平方の定理より,
\( EP^2=(2\sqrt{3})^2+4^2=28 \)
\( EP=2\sqrt{7} \; (cm) \) (\( EP>0 \) より)
以上より,\( △DPE \) において,三平方の定理より,
\( DE^2=\sqrt{21}^2+(2\sqrt{7})^2=49 \)
\( DE=7 \; (cm) \) (\( DE>0 \) より)
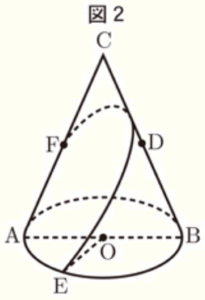
(ウ) 次の の中の「せ」「そ」にあてはまる数字をそれぞれ0~9の中から1つずつ選び,その数字を答えなさい。
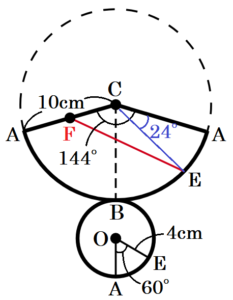
点 \( F \) が線分 \( AC \) の中点であるとき,この円すいの側面上に,図2のように点 \( E \) から線分 \( BC \) と交わるように,点 \( F \) まで線を引く。このような線のうち,長さが最も短くなるように引いた線の長さは \( \fbox{ せ }\sqrt{\fbox{ そ }} \; cm \) である。
【解説】
この円すいを \( CA \) で切って展開すると,右の図のようになります。
側面を展開したおうぎ形の内角は,
\( 360° \times \dfrac{8\pi{}}{20\pi{}}=144° \)
また,\( ∠AOE=60° \) より,
弧 \( AE \) の長さは円 \( O \) の円周の \( \dfrac{1}{6} \) なので,
おうぎ形の弧の長さの \( \dfrac{1}{6} \) でもあります。
ここから,\( ∠ACE=\dfrac{1}{6}∠ACA=24° \)
線分 \( AC \) を延長し,円 \( C \) との交点を \( G \) とすると,
\( ∠ACA=144° \) より,\( ∠ACG=36° \)
\( ∠ACE=24° \) より,\( ∠ECG=24°+36°=60° \)
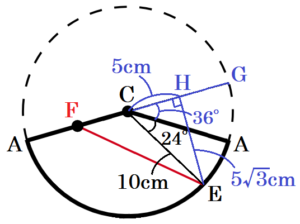
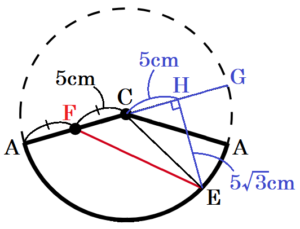
点 \( E \) から線分 \( CG \) に垂線をひき,
交点を点 \( H \) とすると,
\( △ECI \) は \( 30°,60°,90° \) の直角三角形なので,
\( CH=\dfrac{1}{2}EC=5 \; (cm) \)
\( EH=\dfrac{\sqrt{3}}{2}EC=5\sqrt{3} \; (cm) \)
\( △EFH \) において,
点 \( F \) は母線 \( CA \) の中点なので,\( CF=5 \; cm \)
また,\( FH=CF+CH=10 \; cm \) なので,
三平方の定理より,
\( EF^2=10^2+(5\sqrt{3})^2=175 \)
\( EF=5\sqrt{7} \; (cm) \) (\( EF>0 \) より)




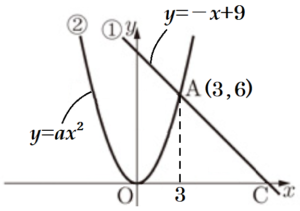





-アイキャッチ-120x68.jpg)
-アイキャッチ-120x68.jpg)