大問1
(1) 次の①~④を計算しなさい。
➀ \( 1-(-3)-9 \)
【解説】
\( =1+3-9 \)
\( =4-9 \)
\( =-5 \)
➁ \( \dfrac{2x+y}{3}-\dfrac{x-3y}{4} \)
【解答】
\( \dfrac{5x+13y}{12} \)
【解説】
\( =\dfrac{4(2x+y)}{12}-\dfrac{3(x-3y)}{12} \)
\( =\dfrac{4(2x+y)-3(x-3y)}{12} \)
\( =\dfrac{8x+4y-3x+9y}{12} \)
\( =\dfrac{5x+13y}{12} \)
➂ \( 2a^2b \times (-3b)^2 \div \dfrac{9}{2}a^2 \)
【解説】
\( =2a^2b \times 9b^2 \times \dfrac{2}{9a^2} \)
\( =\dfrac{=2a^2b \times 9b^2 \times 2}{9a^2} \)
\( =4b^3 \)
➃ \( \sqrt{15}+\sqrt{12} \div \sqrt{5} \)
【解答】
\( \dfrac{7\sqrt{15}}{5} \)
【解説】
\( =\sqrt{15}+2\sqrt{3} \times \dfrac{1}{\sqrt{5}} \)
\( =\sqrt{15}+\dfrac{2\sqrt{3}}{\sqrt{5}} \)
\( =\sqrt{15}+\dfrac{2\sqrt{3} \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}} \)
\( =\sqrt{15}+\dfrac{2\sqrt{15}}{5} \)
\( =\dfrac{7\sqrt{15}}{5} \)
(2) 比例式 \( (x-6):x=4:7 \) について,\( x \) の値を求めなさい。
【解説】
\( 7(x-6)=4x \)
\( 7x-42=4x \)
\( 3x=42 \)
\( x=14 \)
(3) ある生徒の3教科のテストの点数は,それぞれ \( a \) 点,\( b \) 点,\( 90 \) 点であり,その平均点は \( 72 \) 点であった。このとき,\( b \) を \( a \) の式で表しなさい。
【解答】
\( b=-a+126 \) または \( b=126-a \)
【解説】
3教科のテストの平均点を方程式で表すと,
\( \dfrac{a+b+90}{3}=72 \)
なので,\( b \) を \( a \) の式で表すと,
\( a+b+90=216 \)
\( b=-a+126 \)
(4) 2次方程式 \( x^2-4x+3=0 \) の2つの解の和が,\( x \) についての2次方程式 \( x^2+ax-4=0 \) の解の1つになっているとき,\( a \) の値を求めなさい。
【解説】
\( x^2-4x+3=0 \) を解くと,
\( x^2-4x+3=0 \)
\( (x-1)(x-3)=0 \)
\( x=1,3 \)
なので,2つの解の和は \( 4 \) になります。
\( x^2+ax-4=0 \) の解の1つが \( 4 \) であるということは,
\( x=4 \) を代入したときにこの方程式が成り立つので,
\( 4^2+4a-4=0 \)
\( 16+4a-4=0 \)
\( 4a=-12 \)
\( a=-3 \)
(5) \( y \) が \( x \) に反比例するものはどれか。次のア~エからすべて選び,その記号を書きなさい。
ア 定価 \( x \) 円のノートを定価の \( 30\% \) 引きで買ったとき,代金は \( y \) 円である。
イ \( 12 \; km \) の道のりを時速 \( x \; km \) で進んだとき,かかった時間は \( y \) 時間である。
ウ \( x \; mL \) のジュースを4人で均等に分けたとき,1人分のジュースの量は \( y \; mL \) である。
エ 面積が \( 15 \; cm^2 \) の三角形の底辺を \( x \; cm \) としたとき,高さは \( y \; cm \) である。
【解説】
反比例を表す式は \( y=\dfrac{a}{x} \) または \( xy=a \)(\( a \) は定数)になります。
ア~エの関係を式で表すと,
ア ・・・ \( y=(1-0.3)x \) → \( y=0,7x \)
イ ・・・ \( y=\dfrac{12}{x} \)
ウ ・・・ \( y=\dfrac{x}{4} \)
エ ・・・ \( \dfrac{1}{2}xy=15 \) → \( xy=30 \)
なので,あてはまるのはイとエになります。
(6) 3辺の長さが \( \sqrt{10} \; cm,2\sqrt{7} \; cm,3\sqrt{2} \; cm \) である三角形は直角三角形であることを,言葉と式を使って説明しなさい。
【解答】
\( (\sqrt{10})^2+(3\sqrt{2})^2=28 \)
\( (2\sqrt{7})^2=28 \)
より,\( (\sqrt{10})^2+(3\sqrt{2})^2=(2\sqrt{7})^2 \) であり,
三平方の定理が成り立っているので,
3辺の長さが \( \sqrt{10} \; cm,2\sqrt{7} \; cm,3\sqrt{2} \; cm \) である三角形は直角三角形である。
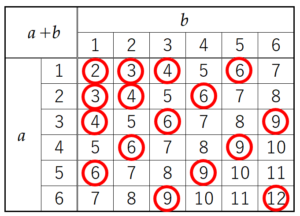
(7) 1から6までの目が出る2つのさいころA,Bを同時に投げるとき,さいころAの出た目の数を \( a \),さいころBの出た目の数を \( b \) とする。このとき,\( \dfrac{36}{a+b} \) が整数となる確率を求めなさい。ただし,さいころはどの目が出ることも同様に確からしいとする。
【解説】
\( \dfrac{36}{a+b} \) が整数になるのは,\( a+b \) の値が \( 36 \) の約数になるときです。
\( 36 \) の約数は \( 1,2,3,4,6,9,12,18,36 \) で,
\( a+b \) が取り得る値の範囲は \( 2≦a+b≦12 \) なので,
あてはまるのは \( 2,3,4,6,9,12 \) のどれかになる場合です。
2つのさいころの出た目の組み合わせと
それぞれの場合の \( a+b \) の値を表に書き出し,
\( a+b \) の値が \( 2,3,4,6,9,12 \) になるところに
○ をつけてみます。
全ての組み合わせは \( 36 \) 通り,
○ がつく組み合わせは \( 16 \) 通りなので,
求める確率は \( \dfrac{16}{36}=\dfrac{4}{9} \)
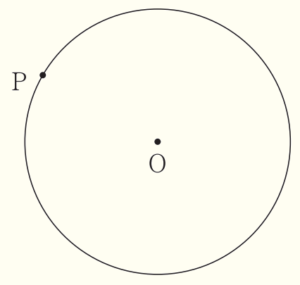
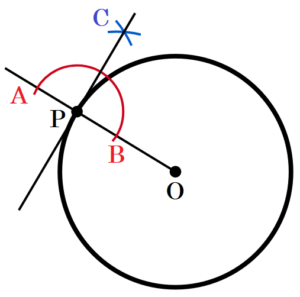
(8) 次の図のような,円 \( O \) がある。円 \( O \) の周上の点 \( P \) を通る接線を,定規とコンパスを使い,作図によって求めなさい。ただし,定規は直線をひくときに使い,長さを測ったり角度を利用したりしないこととする。なお,作図に使った線は消さずに残しておくこと。
【解答・解説】
円の半径と接線は接点において垂直に交わります。
つまり,\( P \) を通る直線 \( OP \) の垂線を描けばいいことになります。
手順1 2点 \( O,P \) を通る直線を描く。
手順2 点 \( P \) を中心に円弧を描く。
(直線 \( OP \) との交点を \( A,B \) とします。)
手順3 2点 \( A,B \) を中心に円弧を描く。
(交点を \( C \) とします。)
手順4 2点 \( C,P \) を通る直線を描く。
直線 \( CP \) が求める接線になります。
大問2
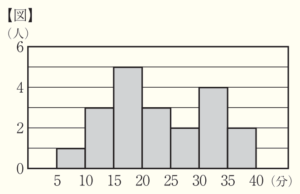
ある中学校の3年1組の生徒20人の通学時間を調査した。右の【図】は,調査の結果をヒストグラムに表したもので,通学時間の平均値は \( 23.0 \) 分であった。このヒストグラムでは,例えば,通学時間が \( 5 \) 分以上 \( 10 \) 分未満の生徒が1人いることがわかる。このとき,次の(1)~(3)の問いに答えなさい。
(1) 通学時間が \( 25 \) 分以上 \( 30 \) 分未満の階級までの累積度数を求めなさい。
【解説】
ある階級の累積度数は,その階級以下のすべての階級の度数の合計になります。
\( 30 \) 分未満の階級の度数の合計は \( 1+3+5+3+2=14 \)(人)
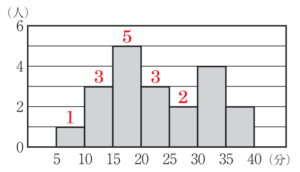
(2) 【図】からわかることとして適切なものはどれか。次のア~エからすべて選び,その記号を書きなさい。
ア 通学時間が平均値以上の生徒は,8人未満である。
イ 通学時間の範囲は,\( 20 \) 分である。
ウ 通学時間が \( 15 \) 分以上 \( 20 \) 分未満の階級の相対度数は,\( 0.25 \) である。
エ 通学時間の第1四分位数は,度数が最も大きい階級に含まれている。
【解説】
ア ・・・ 通学時間の平均値は \( 23.0 \) 分ですが,\( 25 \) 分以上の生徒は \( 2+4+2=8 \)(人)いるので
正しくない。
イ ・・・ 範囲は,「最大値 \( – \) 最小値」で求めることができますが,ヒストグラムからだけでは最大値・
最小値の値を具体的に読み取ることはできないので,範囲を求めることはできません。
最小値は \( 5 \) 分,\( 6 \) 分,\( 7 \) 分,\( 8 \) 分,\( 9 \) 分 のどれか
最大値は \( 35 \) 分,\( 36 \) 分,\( 37 \) 分,\( 38 \) 分,\( 39 \) 分 のどれか
であることしかわかりません。
ウ ・・・ ある階級の相対度数は,「その階級の度数 \( \div \) すべての階級の度数の合計」で求めることが
できるので,\( 15 \) 分以上 \( 20 \) 分未満の階級の相対度数は,\( 5 \div 20=0.25 \) で正しい。
エ ・・・ 全部で20人分のデータを整理しているので,第1四分位数は,時間の短い方から5番目と
6番目の値の平均値になります。5番目と6番目の値はどちらも \( 15 \) 分以上 \( 20 \) 分未満の
階級に含まれており,第1四分位数も \( 15 \) 分以上 \( 20 \) 分未満の階級に含まれるので,正しい。
(3) 3年2組の生徒20人についても通学時間を調査し,結果をヒストグラムに表すと,下のア~エのいずれかになった。1組と2組のヒストグラムを比較すると,次の①~③のことがわかった。このとき,3年2組のヒストグラムとして適切なものを,下のア~エから1つ選び,その記号を書きなさい。
① 度数が最も多い階級は,1組と2組で異なる。
➁ 階級値が \( 32.5 \) 分である階級の度数は,1組よりも2組が少ない。
③ 通学時間の中央値は1組よりも2組が小さい。
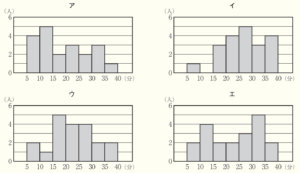
【解説】
➀より,1組の度数が最も多い階級は,\( 15 \) 分以上 \( 20 \) 分未満で,
ウのヒストグラムも度数が最も多い階級は, \( 15 \) 分以上 \( 20 \) 分未満の階級なので,
ウはあてはまりません。
➁より,階級値が \( 32.5 \) 分である階級は,\( 30 \) 分以上 \( 35 \) 分未満の階級です。
1組の \( 30 \) 分以上 \( 35 \) 分未満の階級の度数は \( 4 \) 人なので,
\( 30 \) 分以上 \( 35 \) 分未満の階級の度数が \( 5 \) 人であるエはあてはまりません。
➂より,中央値は,時間の短い方から10番目と11番目の値の平均値になります。
1組について,10番目と11番目の値はどちらも \( 20 \) 分以上 \( 25 \) 分未満の階級に
含まれているので,中央値も \( 20 \) 分以上 \( 25 \) 分未満の階級に含まれます。
イのヒストグラムでは,10番目と11番目の値はどちらも \( 25 \) 分以上 \( 30 \) 分未満の
階級に含まれており,中央値も \( 25 \) 分以上 \( 30 \) 分未満の階級に含まれるので,
イはあてはまりません。
よって,あてはまるヒストグラムはアになります。
大問3
のぞみさんは,昨日の数学の授業で学習した内容について,先生と話をしている。次の【会話】は,のぞみさんと先生の会話である。また,下の【のぞみさんのノート】は,のぞみさんが文字を使って正しく説明したノートの一部である。このとき(1)・(2)の問いに答えなさい。
【会話】
先 生:昨日の授業で,2けたの自然数と,その数の十の位の数と一の位の数を入れかえた数の和は,
必ず \( 11 \) の倍数になることを,文字を使って学習しました。例えば,\( 12 \) と \( 21 \),\( 73 \) と \( 37 \) の
和を考えると,それぞれ \( 33,110 \) となって \( 11 \) の倍数になりますね。実は,\( 12 \) と \( 21 \) を
つないだ \( 1221 \),\( 73 \) と \( 37 \) をつないだ \( 7337 \) のような,千の位の数と一の位の数が等しく,
百の位の数と十の位の数が等しい4けたの自然数も \( 11 \) の倍数になります。
のぞみ:えっ,本当ですか。\( 1221 \) と \( 7337 \) が \( 11 \) の倍数かどうか,実際に計算して確かめてみます。
\( 1221 \) を \( 11 \) でわると \( 111,7337 \) を \( 11 \) でわると \( 667 \) になります。\( 11 \) でわり切れると
いうことは,\( 1221 \) も \( 7337 \) も確かに \( 11 \) の倍数ですね。これが必ず成り立つことを,
昨日学習したように,文字を使って説明してみます。
【のぞみさんのノート】
〔説明〕
4けたの自然数の千の位の数と一の位の数を \( x \),百の位の数と十の位の数を \( y \) とすると
4けたの自然数は ア \( x+ \) イ \( y+10y+x \)
と表される。
このとき,
ア \( x+ \) イ \( y+10y+x \)
\( = \) ウ \( x+ \) エ \( y \)
\( =11( \) オ \( ) \)
オ は整数であるから,\( 11( \) オ \( ) \) は \( 11 \) の倍数である。
したがって,千の位の数と一の位の数が等しく,百の位の数と十の位の数が等しい4けた
の自然数は \( 11 \) の倍数になる。
(1) ア ~ エ に当てはまる数と, オ に当てはまる文字式を,それぞれ書きなさい。
【解答】
ア ・・・ \( 1000 \)
イ ・・・ \( 100 \)
ウ ・・・ \( 1001 \)
エ ・・・ \( 110 \)
オ ・・・ \( 91x+10y \)
【解説】
【4けたの自然数 \( abcd \) を文字式で表す】
例として \( 1234 \) という4けたの自然数は,
\( 1000 \) が \( 1 \) 個,\( 100 \) が \( 2 \) 個,\( 10 \) が \( 3 \) 個,\( 1 \) が \( 4 \) 個
集まってできた数であり,
\( 1000 \times 1+100 \times 2+10 \times 3+1 \times 4 \)
と表すことができます。
ここから,\( abcd \) という任意の4けたの自然数におきかえると,
\( 1000 \times a+100 \times b+10 \times c+1 \times d \)
\( =1000a+100b+10c+d \)
と表すことができます。
【\( 11 \) の倍数】
\( 11 \) の倍数とは,\( 11 \) でわりきれる数のことです。
例えば,\( 33 \) という数は,\( 33 \div 11=3 \) で \( 11 \) でわりきれるので,\( 11 \) の倍数です。
\( 33 \div 11=3 \) を \( 33=11 \times 3 \) と変形すると,
\( 33 \) という数は,\( 11 \) に \( 3 \) という整数をかけた(\( 3 \) 倍した)ものであるともいえます。
ここから,\( 11 \) の倍数とは,\( 11 \) の整数倍になっている数のことなので,
\( 11 \times n=11n \)(\( n \) は整数)
と表すことができます。
(2) 2けたの自然数には,その数から,その数の十の位の数と一の位の数を入れかえた数をひくと \( 36 \) になるものがいくつかあるが,このような2けたの自然数のうち,最も大きな自然数は \( 95 \) である。このことを,もとの自然数の十の位の数を \( a \),一の位の数を \( b \) として,文字を使って説明しなさい。
【解答】
もとの自然数の十の位の数を \( a \),一の位の数を \( b \) とすると,
もとの自然数は \( 10a+b \),入れかえた数は \( 10b+a \)
と表すことができるので,
\( (10a+b)-(10b+a)=36 \)
\( 9(a-b)=36 \)
\( a-b=4 \)
\( a \) は \( 1≦a≦9 \) の自然数なので,
あてはまる \( a,b \) の組み合わせは
\( (a,b)=(9,5),(8,4),(7,3),(6,2),(5,1),(4,0) \)
この中で,\( 10a+b \) が最も大きくなる組み合わせは,\( (a,b)=(9,5) \) のときである。
したがって,もとの自然数から入れかえた数をひくと \( 36 \) になる最も大きな自然数は \( 95 \) である。
大問4
ある道の駅で,自転車の貸し出しを行っている。次の表は,自転車の貸し出しの料金表である。この道の駅では,借りる日の前日までに予約をすると,自転車1台につき基本料金を \( 100 \) 円値引きしている。このとき,下の(1)・(2)の問いに答えなさい。
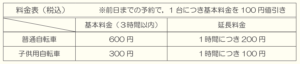
(1) 普通自転車 \( a \) 台と子供用自転車 \( b \) 台を2時間半,予約をせずに当日借りたところ,料金の合計は \( 5000 \) 円以下であった。この数量の関係を不等式で表しなさい。
【解答】
\( 600a+300b≦5000 \)
【解説】
借りた時間は2時間半で3時間以内なので,必要な料金は基本料金だけです。
普通自転車 \( a \) 台を借りるのに必要な料金は \( 600a \) 円,
子供用自転車 \( b \) 台を借りるのに必要な料金は \( 300b \) 円
と表すことができます。
これらの合計が \( 5000 \) 円以下なので,
不等式で表すと,\( 600a+300b≦5000 \)
(2) サイクリングに行く計画を立て,サイクリングの前日までに普通自転車4台,子供用自転車6台の合計10 台の自転車を予約した。当日になって,新たに普通自転車と子供用自転車をそれぞれ何台か借り,合計16台でサイクリングをした。10時から15時まで自転車を借りたときの,料金の合計が \( 10000 \) 円だったとき,当日新たに借りた普通自転車と子供用自転車の台数をそれぞれ求めなさい。
【解答】
普通自転車 ・・・ \( 2 \) 台
子供用自転車 ・・・ \( 4 \) 台
【解説】
10時から15時までの \( 5 \) 時間自転車を借りたということは,
\( 3 \) 時間分の基本料金と \( 2 \) 時間分の延長料金がかかります。
まず,予約していた分の自転車にかかる料金について考えると,
普通自転車 \( 4 \) 台を \( 5 \) 時間借りるのに必要な料金は
\( (600-100+200 \times 2) \times 4=3600 \)(円)
子供用自転車 \( 6 \) 台を \( 5 \) 時間借りるのに必要な料金は
\( (300-100+100 \times 2) \times 6=2400 \)(円)
になります。
次に,予約なしの分の自転車にかかる料金について考えます。
予約なしで借りた普通自転車を \( x \) 台,子供用自転車を \( y \) 台とすると,
普通自転車 \( x \) 台を \( 5 \) 時間借りるのに必要な料金は
\( (600+200 \times 2) \times x=1000x \)(円)
子供用自転車 \( y \) 台を \( 5 \) 時間借りるのに必要な料金は
\( (300+100 \times 2) \times y=500y \)(円)
と表すことができます。
これらの料金の合計が \( 10000 \) 円なので,
\( 3600+2400+1000x+500y=10000 \) ・・・ ➀
予約なしで借りた自転車の合計は \( 6 \) 台なので,
\( x+y=6 \) ・・・ ➁
➀➁を連立方程式として解くと,
\( \left\{ \begin{array}{}
3600+2400+1000x+500y=10000 \;\; ・・・ ➀ \;\; \\
x+y=6 \;\; ・・・ ➁ \;\; \\
\end{array} \right. \)
➀を整理すると,
\( 2x+y=8 \) ・・・ ➀’
➀’\( – \) ➁ すると,
\( x=2 \)
➁に代入すると,
\( 2+y=6 \)
\( y=4 \)
大問5
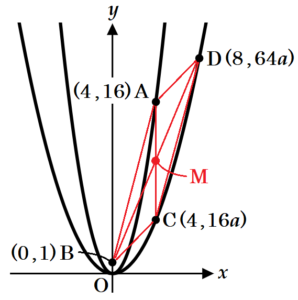
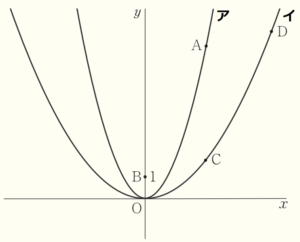
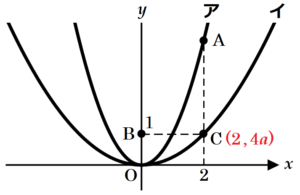
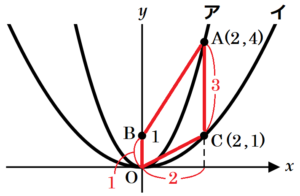
下の図において,ア は関数 \( y=x^2 \) のグラフ,イ は関数 \( y=ax^2 \;\; (0<a<1) \) のグラフである。点 \( A \) はアのグラフ上にあり,点 \( B \) の座標は \( (0,1) \) で,点 \( C \) と点 \( D \) はイのグラフ上にある。また,点 \( A \) と点 \( C \) の \( x \) 座標は等しく,点 \( D \) の \( x \) 座標は点 \( C \) の \( x \) 座標より大きい。このとき,次の(1)・(2)の問いに答えなさい。
(1) 点 \( A \) の \( x \) 座標が \( 2 \) であり,点 \( B \) と点 \( C \) の \( y \) 座標が等しいとき,次の①,②の問いに答えなさい。
① \( a \) の値を求めなさい。
【解答】
\( a=\dfrac{1}{4} \)
【解説】
点 \( C \) は \( y=ax^2 \) 上の点で,\( x \) 座標は \( 2 \)
なので,\( y \) 座標は \( 4a \) と表すことができます。
点 \( B \) と点 \( C \) の \( y \) 座標が等しいとき,
点 \( C \) の \( y \) 座標は \( 1 \) なので,
\( 4a=1 \)
\( a=\dfrac{1}{4} \)
② 四角形 \( OCAB \) の面積を求めなさい。
【解説】
点 \( A \) は \( y=x^2 \) 上の点で,
\( x \) 座標は \( 2 \) なので,\( y \) 座標は
\( y=2^2=4 \)
になります。
また,点 \( B \) と点 \( C \) の \( y \) 座標が等しいとき,
点 \( C \) の \( y \) 座標は \( 1 \) です。
四角形 \( OCAB \) は \( OB//CA \) の台形なので,
面積は,
\( (1+3) \times 2 \times \dfrac{1}{2}=4 \)
(2) 点 \( A \) の \( x \) 座標を \( 4 \) とする。点 \( A \) と点 \( B \),点 \( B \) と点 \( C \),点 \( C \) と点 \( D \),点 \( D \) と点 \( A \) をそれぞれ結ぶと,平行四辺形になった。このとき,\( a \) の値を求めなさい。
【解答】
\( a=\dfrac{5}{16} \)
【解説】
点 \( A,C \) の \( x \) 座標は \( 4 \) なので,
点 \( A \) の座標は \( A(4,16) \),点 \( C \) の座標は \( C(4,16a) \) になります。
平行四辺形の対角線はそれぞれの中点で交わるので,対角線の交点を \( M \) とすると,
\( M \) は線分 \( AC \) の中点なので,\( y \) 座標は \( \dfrac{16a+16}{2} \) ・・・ ➀ と表すことができます。
また,\( M \) は線分 \( BD \) の中点でもあり,
点 \( B \) の \( x \) 座標は \( 0 \),点 \( M \) の \( x \) 座標は \( 4 \) なので,
点 \( D \) の \( x \) 座標は \( 8 \) になります。
点 \( D \) は \( y=ax^2 \) 上の点で,\( x \) 座標は \( 8 \) なので,
\( y \) 座標は \( 64a \) と表すことができます。
このとき,点 \( B \) の \( y \) 座標は \( 1 \) であることから,
\( M \) の \( y \) 座標は \( \dfrac{1+64a}{2} \) ・・・ ➁ と表すことができます。
➀➁より,
\( \dfrac{16a+16}{2}=\dfrac{1+64a}{2} \)
\( 16a+16=1+64a \)
\( 48a=15 \)
\( a=\dfrac{5}{16} \)
大問6
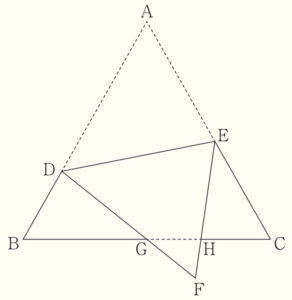
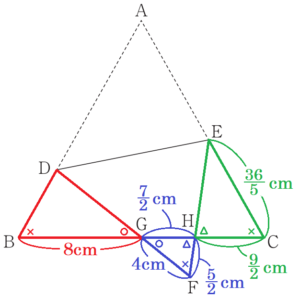
右の図のように,正三角形 \( ABC \) の辺 \( AB \) 上に \( AD>DB \) となる点 \( D \),辺 \( AC \) 上に \( AE>EC \) となる点 \( E \) をとり,線分 \( DE \) を折り目として頂点 \( A \) を折り返し,頂点 \( A \) が移った点を \( F \) とする。また,辺 \( BC \) と線分 \( DF \) との交点を \( G \),辺 \( BC \) と線分 \( EF \) との交点を \( H \) とする。このとき,次の(1)・(2)の問いに答えなさい。
(1) \( △BGD \) ∽ \( △FGH \) を証明しなさい。
【解答】
\( △BGD \) と \( △FGH \) において,
正三角形の内角なので,
\( ∠GBD=∠GFH=60° \) ・・・ ➀
対頂角は等しいので,
\( ∠BGD=∠FGH \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △BGD \) ∽ \( △FGH \)
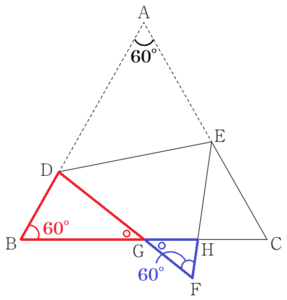 参考:点 \( A \) と点 \( F \) は折り返す前後の点なので,
参考:点 \( A \) と点 \( F \) は折り返す前後の点なので,
\( ∠BAC=∠GFH=60° \)
(2) 正三角形 \( ABC \) の1辺の長さを \( 16 \; cm \) とし,三角形 \( BGD \) の3辺の長さを,\( BG=8 \; cm,GD=7 \; cm,DB=5 \; cm \) とする。このとき,線分 \( CE \) の長さを求めなさい。
【解答】
\( CE=\dfrac{36}{5} \; cm \)
【解説】
(1)より,\( △BGD \) ∽ \( △FGH \) であることがわかっていて,
同様の考え方から,\( △FGH \) ∽ \( △CEH \) でもあることもわかります。
\( △BGD \) の3辺の長さはわかっているので,\( △FGH \) のどれか1辺の長さがわかれば,
\( CE \) の長さを求めることができます。
\( AB=16 \; cm,DB=5 \; cm \) より,\( AD=11 \; cm \) であり,
\( FD=AD=11 \; cm ,GD=7 \; cm \) なので,
\( FG=4 \; cm \) になっています。
(1)より,\( △BGD \) ∽ \( △FGH \) なので,
\( BG:FG= 8:4 \) であり,相似比は \( 2:1 \) です。
ここから,
\( DG:HG=2:1 \)
\( 7:HG=2:1 \)
\( HG=\dfrac{7}{2} \; (cm) \)
\(BD:FH=2:1 \)
\( 5:FH=2:1 \)
\( FH=\dfrac{5}{2} \; (cm) \)
また,\( △FGH \) ∽ \( △CEH \) でもあり,
\( AB=16 \; cm,BG=8 \; cm,HG=\dfrac{7}{2} \; cm \) より,
\( CH=\dfrac{9}{2} \; cm \) になっています。
ここから,\( FH:CH=\dfrac{5}{2}:\dfrac{9}{2} \) より,
相似比は \( 5:9 \) であり,
\( FG:CE=5:9 \)
\( 4:CE=5:9 \)
\( CE=\dfrac{36}{5} \; (cm) \)





 参考:点 \( A \) と点 \( F \) は折り返す前後の点なので,
参考:点 \( A \) と点 \( F \) は折り返す前後の点なので,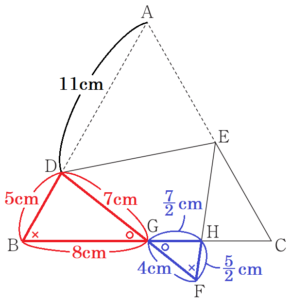
-アイキャッチ-120x68.jpg)
