22
大問1
(1) \( 3+(-7) \) を計算しなさい。
【解説】
\( =3-7 \)
\( =-4 \)
(2) \( \dfrac{4}{3} \div \left( -\dfrac{5}{12} \right) \) を計算しなさい。
【解答】
\( -\dfrac{16}{5} \)
【解説】
\( =\dfrac{4}{3} \times \left( -\dfrac{12}{5} \right) \)
\( =-\dfrac{4 \times 12}{3 \times 5} \)
\( =-\dfrac{16}{5} \)
(3) \( x \) 枚の折り紙を,1人に \( 10 \) 枚ずつ \( y \) 人に配ると \( 4 \) 枚余る。このときの数量の関係を等式に表しなさい。
【解説】
1人に \( 10 \) 枚ずつ \( y \) 人に配るのに必要な折り紙の枚数は \( 10y \) 枚と表すことができます。
全部で \( x \) 枚の折り紙を, \( 10y \) 枚配った残り(余り)が \( 4 \) 枚なので,
この関係を等式に表すと,
\( x=10y+4 \)
(4) 連立方程式 \( \left\{ \begin{array}{}
4x+7y=-2 \\
3x-2y=13 \\
\end{array} \right. \) を解きなさい。
【解説】
\( \left\{ \begin{array}{}
4x+7y=-2 \;\; ・・・ \;\; ➀ \\
3x-2y=13 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( \times 3 \) すると,
\( 12x+21y=-6 \) ・・・ ➀’
➁ \( \times 4 \) すると,
\( 12x-8y=52 \) ・・・ ➁’
➀’\( – \) ➁’ すると,
\( 29y=-58 \)
\( y=-2 \)
➀ に代入すると,
\( 4x+7 \times (-2)=-2 \)
\( 4x=12 \)
\( x=3 \)
(5) \( a=15,b=6 \) のとき,次の式の値を求めなさい。
\( a^2-4ab+4b^2 \)
【解説】
与式を因数分解すると,\( a^2-4ab+4b^2=(a-2b)^2 \) なので,
ここに \( a=15,b=6 \) を代入すると,
\( (a-2b)^2=(15-2 \times 6)^2 \)
\( =3^2 \)
\( =9 \)
(6) 2つのさいころを同時に投げるとき,次のアとイでは,どちらの方が起こりやすいといえますか。起こりやすい方の記号と確率を答えなさい。
ただし,2つのさいころの1から6の目は,どの目が出ることも同様に確からしいとする。
ア 出る目の数の和が \( 6 \) である
イ 出る目の数の積が \( 6 \) である
【解答】
ア 出る目の数の和が \( 6 \) である
確率 ・・・ \( \dfrac{5}{36} \)
【解説】
2つのさいころにA,Bと名前をつけ,
ア,
イそれぞれの場合について起こる確率を求めます。
【出る目の数の和が \( 6 \) である確率】
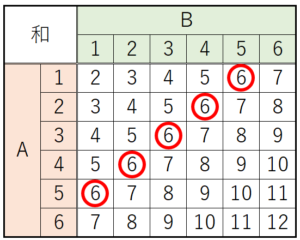
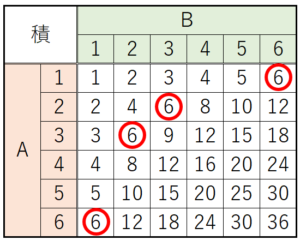
さいころA,Bの出る目の組み合わせを表にすると,
和が \( 6 \) になる組み合わせは \( 5 \) 通り,
すべての組み合わせは \( 36 \) 通りなので,
おこる確率は \( \dfrac{5}{36} \)
【出る目の数の積が \( 6 \) である確率】
さいころA,Bの出る目の組み合わせを表にすると,
積が \( 6 \) になる組み合わせは \( 4 \) 通り,
すべての組み合わせは \( 36 \) 通りなので,
おこる確率は \( \dfrac{4}{36} \)
よって,「ア 出る目の数の和が \( 6 \) である」の方が起こりやすいといえます。
(7) 右の図は,ある地域の2010年3月と2024年3月の日平均気温をもとに,横軸を気温,縦軸を相対度数として度数分布多角形に表したものである。
これらの度数分布多角形から,「日平均気温は,2010年3月より2024年3月の方が高い傾向にある」と主張することができる。このように主張することができる理由を,2つの度数分布多角形の特徴を比較して説明しなさい。
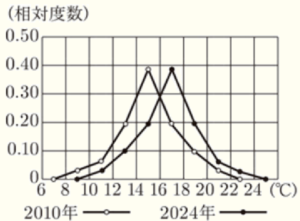
【解答】
2つの度数分布多角形の形はほぼ同じで,2024年3月の度数分布多角形の方が右側にあるから
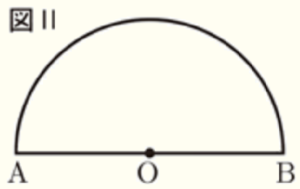
(8) 図Ⅰのような半円の形をしたピザがある。瑞希さんは,包丁を使ってピザを6等分するためには,ピザのどの部分に切れ目を入れればよいか考え,図Ⅱをかいて調べることにした。
図Ⅱにおいて,点 \( O \) は半円の中心,線分 \( AB \) は半円の直径を表している。点 \( O \) を通り,線分 \( OA \) の方から順番に切れ目を入れていくとき,1つ目の切れ目にあたる直線 \( OP \) を,コンパスと定規を使って作図しなさい。作図に用いたは線は消さずに残しておくこと。
ただし, 点 \( P \) は \( \stackrel{\huge\frown}{ AB } \) との交点とする。
【解答】
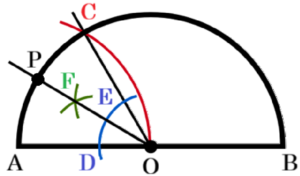
手順1 点 \( A \) を中心に線分 \( OA \) を半径とする
円弧を描く
( \( \stackrel{\huge\frown}{ AB } \) との交点を \( C \) とします。)
手順2 2点 \( O,C \) を通る直線を描く
手順3 点 \( O \) を中心に円弧を描く
( 線分 \( OA \),直線 \( OC \) との交点を \( D,E \) とします。)
手順4 2点 \( D,E \) を中心に円弧を描く
( 交点を \( F \) とします。)
手順5 2点 \( O,F \) を通る直線を描く
手順5の直線と \( \stackrel{\huge\frown}{ AB } \) との交点が求める点 \( P \) になります。
【解説】
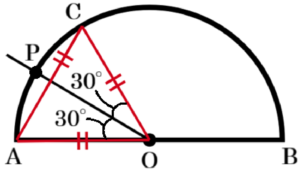
半円(中心角 \( 180° \))を6等分してできるおうぎ形の中心角は \( 30° \) になります。
\( 30° \) は \( 60° \) の半分の大きさであることに注目し,
\( \stackrel{\huge\frown}{ AB } \) 上に \( ∠AOC=60° \) となるような点 \( C \) をとると,
\( OA,OC \) はどちらも半円の半径なので,
\( △OAC \) は内角の1つが \( 60° \) の二等辺三角形,つまり,正三角形になります。
ここから,正三角形 \( OAC \) を作図し,
さらに,\( ∠AOC \) の二等分線を作図することで,
\( ∠AOP=30° \) となるような直線 \( OP \) を作図することができます。
なお,正三角形 \( OAC \) を作図するためには,
点 \( A \) を中心に線分 \( OA \) を半径とする円弧を描くことで,
\( OA=AC \) となるような点 \( C \) を求めることができます。
大問2
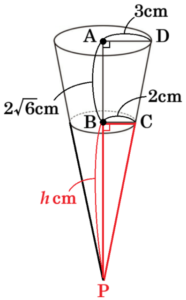
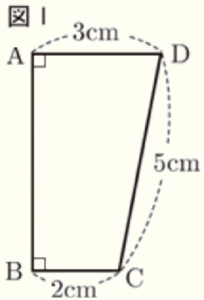
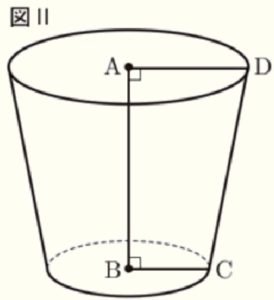
図Ⅰのような \( AD=3 \; cm,BC=2 \; cm,DC=5 \; cm \),\( AD//BC \) の台形 \( ABCD \) がある。また,図Ⅱは,図Ⅰを直線 \( AB \) を回転の軸として1回転させてできる立体である。
このとき,次の1~3の問いに答えなさい。
1 次のア~エの立体について,回転体とみることができないものを1つ選び,記号で答えなさい。
ア 円柱 イ 四角柱 ウ 円錐 エ 球
【解説】
回転体とは,
図Ⅱの立体のように,ある図形をある直線を回転の軸として1回転させてできる立体のことです。
また,回転体には曲面が必ず含まれます。
【イ 四角柱
】は6つの面がすべて平面(四角形)でできているので回転体ではありません。
ア 円柱 ・・・ 長方形の1辺を直線 \( l \) を軸として1回転させた立体
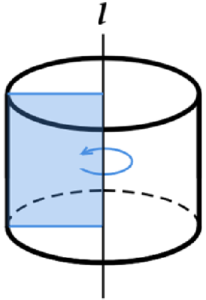
ウ 円錐 ・・・ 直角三角形の直角をなす1辺を含む直線 \( l \) を軸として1回転させた立体
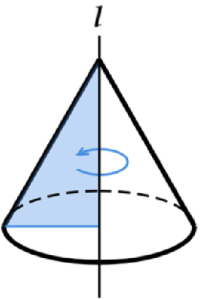
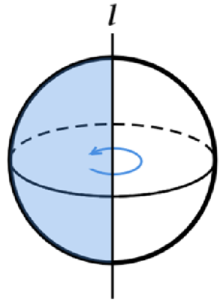
エ 球 ・・・ 半円の直径部分を含む直線 \( l \) を軸として1回転させた立体
2 図Ⅱの立体について,次の(1),(2)の問いに答えなさい。
ただし,円周率は \( \pi{} \) とする。
(1) 線分 \( AB \) の長さを求めなさい。
【解答】
\( AB=2\sqrt{6} \; cm \)
【解説】
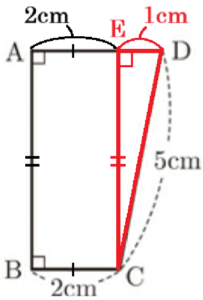
台形 \( ABCD \) において,点 \( C \) から辺 \( AD \) に垂線をひいた交点を \( E \) とすると,
\( AB⊥AD,BC//AD \) より,
\( AE=BC=2 \; cm \) なので,\( ED=1 \; cm \) に
なっています。
直角三角形 \( CDE \) において,三平方の定理より,
\( CE^2=5^2-1^2=24 \)
\( CE=2\sqrt{6} \; (cm) \)(\( CE>0 \) より)
\( AB⊥AD,CE⊥AD \) より,\( AB=CE=2\sqrt{6} \; cm \)
(2) 体積を求めなさい。
【解答】
\( \dfrac{38\sqrt{6}}{3}\pi{} \; cm^3 \)
【解説】
図Ⅱの立体は大きい円すいから小さい円すいを取り除いた形になっています。
大きい円すいの頂点を \( P \) とすると,
\( △PBC \) ∽ \( △PAD \) であり,
\( PB=h \; cm \) とすると,
\( AD=3 \; cm,BC=2 \; cm \) より,
\( PB:PA=BC:AD \)
\( h:(h+2\sqrt{6})=2:3 \)
\( 3h=2h+4\sqrt{6} \)
\( h=4\sqrt{6} \; (cm) \)
大きい円すいの体積を \( V_1 \) とすると,
\( V_1=(\pi{} \times 3^2) \times (4\sqrt{6}+2\sqrt{6}) \times \dfrac{1}{3} \)
\( =18\sqrt{6}\pi{} \; (cm^3) \)
小さい円すいの体積を \( V_2 \) とすると,
\( V_2=(\pi{} \times 2^2) \times 4\sqrt{6} \times \dfrac{1}{3} \)
\( =\dfrac{16\sqrt{6}}{3}\pi{} \; (cm^3) \)
図Ⅱの立体の体積を \( V \) とすると,
\( V=V_1-V_2 \)
\( =18\sqrt{6}\pi{}-\dfrac{16\sqrt{6}}{3}\pi{} \)
\( =\dfrac{38\sqrt{6}}{3}\pi{} \; (cm^3) \)
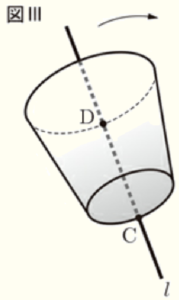
3 図Ⅲは,直線 \( l \) をひいた平らな床の上に,図Ⅱの立体を置いたものである。直線 \( l \) と立体の線分 \( DC \) は重なっており,この状態から矢印の方向に立体をすべらないように転がすと,立体は床の上を転がり続けて,もとの位置に戻った。
このとき,立体はもとの位置に戻るまでに何回転したか求めなさい。
ただし,立体が転がるときの立体の変形は考えないものとする。
【解説】
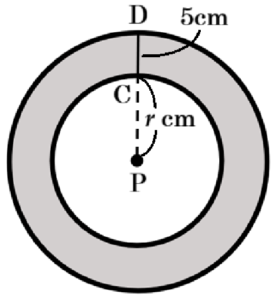
図Ⅲの状態から図Ⅱの立体を転がしたとき,立体の側面は右の図の灰色の部分を動きます。
また,このときできる円の中心は2の大きい円すいの頂点 \( P \) にあたる点になります。
右の図の大きい円の円周の長さは,図Ⅱの立体の円 \( A \) の円が転がった長さと等しくなります。
\( PC=r \; cm \) とすると,2の \( △PBC \) と \( △PAD \) において,
\( PC:PD=BC:AD \)
\( r:(r+5)=2:3 \)
\( 3r=2r+10 \)
\( r=10 \; (cm) \)
であり,右の図の大きい円の円周の長さは,
\( 2 \times \pi{} \times (10+5)=30\pi{} \; (cm) \)
図Ⅱの立体を転がしてもとの位置に戻るまでに \( n \) 回転したとすると,
図Ⅱの立体の円 \( A \) が転がった長さは,
\( 2 \times \pi{} \times 3 \times n=6\pi{}n \; (cm) \)
と表すことができます。
よって,
\( 6\pi{}n=30\pi{} \)
\( n=5 \)(回転)
大問3
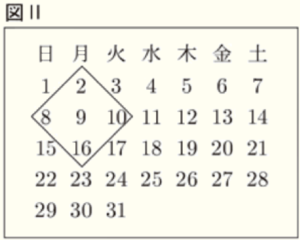
浩太さんと陽香さんは,カレンダーに並んでいる整数を正方形で囲み,その整数の和には,どんな性質があるか調べることにした。
このとき,後の1~3の問いに答えなさい。
1 浩太さんは,図Ⅰのように,ア~ウの正方形で4つの整数を囲んだ。次の【会話Ⅰ】は,それぞれの整数の和について,陽香さんと話し合っている場面である。【会話Ⅰ】の下線部について,後の(1),(2)の問いに答えなさい。
【会話Ⅰ】
浩太:アの正方形は,4つの整数が \( 1,2,8,9 \) だから,その和は \( 1+2+8+9=20 \) だね。
陽香:同じように考えると,イの整数の和は \( 32 \) で,ウの整数の和は \( 108 \) だから,正方形で囲まれた
4つの整数の和は,偶数になると予想できるね。
浩太:確かにそうだけど,アは \( 20=4 \times 5 \),イは \( 32=4 \times 8 \) と表されるから,\( 4 \) の倍数になると
予想することもできるよ。
陽香:なるほど。『正方形で囲まれた4つの整数の和は,\( 4 \) の倍数である』ことを,文字式を使って説明
してみよう。
(1) 下線部①について,浩太さんは,ウの正方形のときも,囲まれた4つの整数の和が \( 4 \) の倍数になることを次のように確かめた。□に当てはまる式を答えなさい。
\( 23+24+30+31=108=\boxed{ } \)
【解説】
【会話Ⅰ】の中のアの正方形,イの正方形の例と同様に \( 4 \times ? \) の形で表します。
(2) 下線部②について,陽香さんは,予想が正しいことを説明するための手順を考え,次の【説明Ⅰ】を完成させた。【説明Ⅰ】の矢印( → ) で示された部分に用いた手順として,最も適切なものを,下のア~オから1つ選び,記号で答えなさい。
【説明Ⅰ】
\( n \) を自然数として,正方形の4つの整数のうち,左上の数を \( n \) と表すと,右上の数は \( n+1 \),
左下の数は \( n+7 \),右下の数は \( n+8 \) と表される。
これらの和は,
\( n+(n+1)+(n+7)+(n+8)=4n + 16 \)
\( =4(n+4) \)
\( n+4 \) は整数だから,\( 4(n+4) \) は \( 4 \) の倍数である。
したがって,正方形で囲まれた4つの整数の和は,\( 4 \) の倍数である。
ア 4つの整数の和を式で表し,計算する。
イ 共通因数をくくり出し,因数分解する。
ウ 計算した式の意味を読みとって,結論を導く。
エ \( 4 \) の倍数であることを示すために,計算結果を変形する。
オ \( n \) を自然数として,4つの整数をそれぞれ文字式で表す。
【解答】
エ \( 4 \) の倍数であることを示すために,計算結果を変形する。
【解説】
「\( 4 \) の倍数」とは,\( 4 \) の整数倍になる数のことです。
ここから,\( 4 \) の倍数であることを証明するためには,
\( 4 \times ? \) の形に変形できることを示せばいいことになります。
2 【説明Ⅰ】の \( 4(n+4) \) という式から,正方形で囲まれた4つの整数の和について,\( 4 \) の倍数であることのほかに,どんなことがいえるか考えた。次の【会話Ⅱ】は,2人が話し合っている場面である。
【会話Ⅱ】
浩太:\( 4(n+4) \) は,\( (n+4) \) の \( 4 \) 倍ということだよね。\( (n+4) \) は,何を表しているのかな。
陽香:【説明Ⅰ】の4つの整数の中に, \( (n+4) \) はないね。図Ⅰのアの正方形で考えてみよう。
アの正方形は 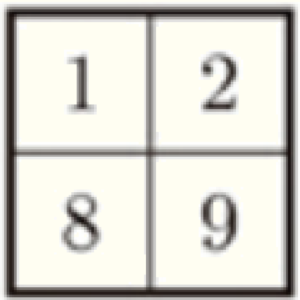 だね。\( 20=4 \times 5 \) の \( 5 \) は,どこかに隠れていないかな。
だね。\( 20=4 \times 5 \) の \( 5 \) は,どこかに隠れていないかな。
浩太:見つけたよ。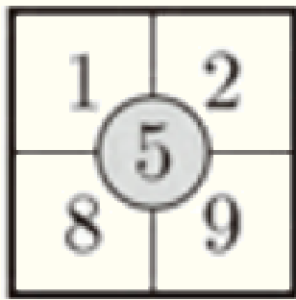 をみて! \( 5 \) は左上の数 \( 1 \) と右下の数 \( 9 \) の和の半分になっているよね。
をみて! \( 5 \) は左上の数 \( 1 \) と右下の数 \( 9 \) の和の半分になっているよね。
右上の数 \( 2 \) と左下の数 \( 8 \) のときも,和の半分は \( 5 \) になるよ。
陽香:すごい。浩太さんの考えを文字式を使って整理すると,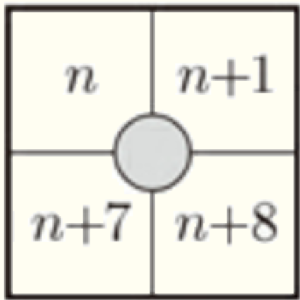 と表されるから,
と表されるから,
● に入る式は \( (n+4) \) になるのかな。
浩太:文字式を計算して確かめると,左上の数と右下の数の和の半分は \( (n+4) \) になるね。
陽香:同じように,右上の数 \( (n+1) \) と左下の数 \( (n+7) \) の和の半分も \( (n+4) \) になるよ。
浩太:正方形で囲まれた4つの整数の和は,\( 4 \) の倍数であることだけでなく,『正方形の真ん中に
ある数 ● の \( 4 \) 倍である』こともいえるね。
【会話Ⅱ】の下線部について,右上の数と左下の数の和の半分が \( (n+4) \) になることを示す計算をかきなさい。
ただし,計算の過程では,\( (n+1) \) と \( (n+7) \) の両方の文字式を用いること。
【解答】
\( \dfrac{(n+1)+(n+7)}{2}=\dfrac{2n+8}{2} \)
\( =n+4 \)
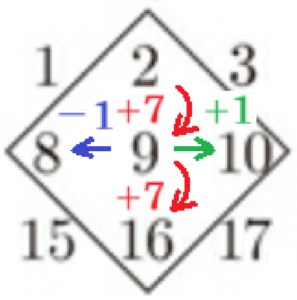
3 2人は,【会話Ⅱ】で発見したことをもとに,図Ⅱのように,正方形の向きと大きさを変えて,5つの整数を囲み,次のことを予想した。
【予想】
正方形の四すみにある4つの整数の和は,真ん中にある数の \( 4 \) 倍である。
この【予想】が正しいことを文字式を使って説明した。下の【説明Ⅱ】の ➀ ~ ➂ に当てはまる式を答えなさい。また, ④ をうめて,【説明Ⅱ】を完成させなさい。
ただし,図Ⅱのように,正方形で5つの整数を囲むとき,四すみにある4つの整数は,上,左,右,下の数を,それぞれ \( 2,8,10,16 \) とする。また,真ん中にある数は \( 9 \) とする。
【説明Ⅱ】
\( n \) を自然数として,正方形の5つの整数のうち,上の数を \( n \) と表すと,左の数は ➀ ,
右の数は ➁ ,下の数は ➂ と表される。
これらの和は,
➃
したがって,正方形の四すみにある4つの整数の和は,真ん中にある数の \( 4 \) 倍である。
【解答】
➀ ・・・ \( n+6 \)
➁ ・・・ \( n+8 \)
➂ ・・・ \( n+14 \)
➃ ・・・ \( n+(n+6)+(n+8)+(n+14)=4n+28 \)
\( =4(n+7) \)
\( n+7 \) は真ん中にある数なので,
\( 4(n+7) \) は真ん中にある数の \( 4 \) 倍である。
【解説】
1週間は7日あるので,ある整数の1つ下に並ぶ整数は \( 7 \) 大きい数,1つ左に並ぶ整数は \( 1 \) 小さい数,1つ右に並ぶ整数は \( 1 \) 大きい数になっています。
これをもとに,図Ⅱの例で考えると,
上の数 ・・・ \( 2=n \)
真ん中にある数 ・・・ \( 9=2+7=n+7 \)
左の数 ・・・ \( 8=2+7-1=n+6 \)
右の数 ・・・ \( 10=2+7+1=n+8 \)
下の数 ・・・ \( 16=2+7+7=n+14 \)
となります。
\( \phantom{ } \)
大問4
志帆さんと直樹さんは,タブレット端末のソフトを使って,グラフを作成している。図Ⅰは,ソフトの【機能】を用いて,関数 \( y=x^2 \) のグラフを表示したものである。
このとき,後の1,2の問いに答えなさい。
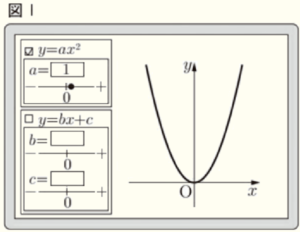
【機能】
・ 関数を選び,\( \boxed{ } \) に値を入力すると,グラフが表示される。
・ 文字の値は
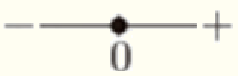
を使って変えることができる。
ボタン (●) を左に動かすと値はだんだん小さくなり,
右に動かすとだんだん大きくなる。
・ 複数のグラフを作成し,同時に表示することができる。
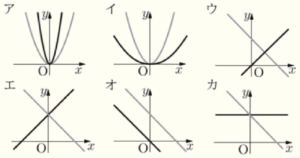
1 【会話Ⅰ】は,関数 \( y=ax^2 \) と関数 \( y=bx+c \) のグラフについて,\( a,b,c \) の値によってグラフがどのように変化するかを,2人が調べている場面である。 ① ~ ➂ に当てはまるグラフの変化として正しいものを,後のア~カから1つずつ選び,それぞれ記号で答えなさい。
ただし,変化する前のグラフを薄い線 (-),変化した後のグラフを濃い線 (-) で表している。
【会話Ⅰ】
志帆:図Ⅰは,\( y=ax^2 \) を選んで \( a \) に \( 1 \) を入力したから,\( y=x^2 \) のグラフが表示されているね。
\( a \) のボタン (●) を動かすと,グラフの開き方がどのように変わるのかな。
直樹:\( a \) のボタンを右に動かすと,\( a \) の値は \( 1 \) より大きくなって,グラフは ① のように変化したよ。
\( y=bx+c \) のグラフではどうかな。
志帆:\( b \) に \( -1 \), \( c \) に \( 6 \) を入力すると,\( y=-x+6 \) のグラフができるよ。\( b=-1 \) と \( c=6 \) の
状態から,どちらか一方のボタンを動かして,グラフの変化を調べてみようよ。
直樹:\( b \) の値は変えずに,\( c \) のボタンを \( 0 \) に合わせると,グラフは ➁ のように変化し,\( c \) の値は
変えずに,\( b \) のボタンを \( 0 \) に合わせると,グラフは ➂ のように変化するね。
【解答】
➀ ・・・ ア
➁ ・・・ オ
➂ ・・・ カ
【解説】
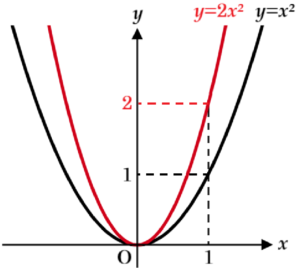
➀ ・・・ \( y=ax^2 \; (a>0) \) のグラフでは,\( a \) の値が大きくなるほどグラフの開きは小さくなります。
例として,\( y=x^2 \) と \( y=2x^2 \) のグラフを考えると下の図のようになります。
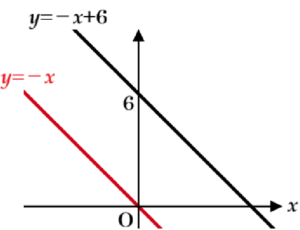
➁ ・・・ \( y=bx+c \) に \( b=-1,c=0 \) を代入すると,\( y=-x \) なので,
グラフは下の図のようになります。
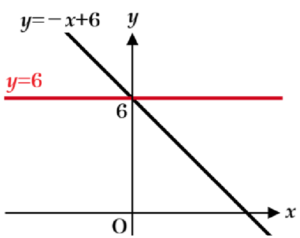
➂ ・・・ \( y=bx+c \) に \( b=0,c=6 \) を代入すると,\( y=6 \) なので,
グラフは下の図のようになります。
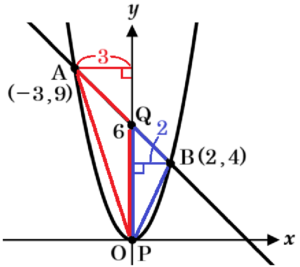
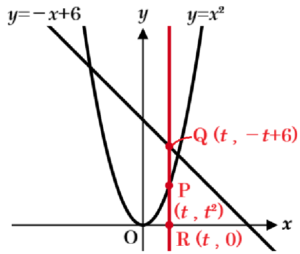
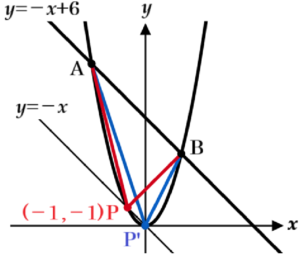
2 図Ⅱは,関数 \( y=x^2 \) ・・・ ❶ と関数 \( y=-x+6 \) ・・・ ❷ と \( x=t \) のグラフを同時に表示し,点 \( A,B,P,Q,R \) を,次の【設定】にしたがって定めたものである。下の【会話Ⅱ】は,\( t \) の値によって変化する点や図形について,2人が調べている場面である。
このとき,後の(1)~(3)の問いに答えなさい。
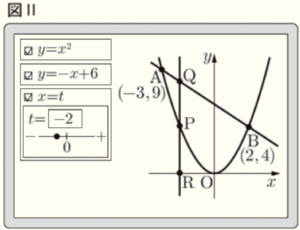
【設定】
・ \( x=t \) と ❶ のグラフの交点を \( P \),\( x=t \) と ❷ のグラフの交点を \( Q \),
\( x=t \) と \( x \) 軸との交点を \( R \) とする。
・ ❶ と ❷ のグラフの交点を \( A,B \) とし,座標を表示する。
・ \( t \) の変域は,\( -3≦t≦2 \) とする。
【会話Ⅱ】
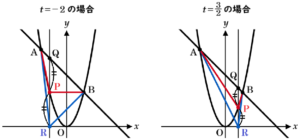
直樹:\( t \) に \( -2 \) を入力すると,点 \( Q \) の座標は ➃ になったよ。
このとき,点 \( P \) は線分 \( QR \) の中点になるね。\( t \) の値を少しずつ大きくしてみよう。
志帆:\( t=0 \) のときは,点 \( P \) は原点 \( O \) と重なるね。
このとき,\( △APB \) の面積は ➄ になるね。
直樹:ほら見て。点 \( P \) が線分 \( QR \) の中点になるときが,もう1つあったよ。
志帆:本当だね。そのときの \( t \) の値は,\( t= \) ⑥ だね。
(1) 【会話Ⅱ】の ➃ に当てはまる座標を答えなさい。
【解説】
点 \( Q \) は \( y=-x+6 \) と \( x=-2 \) の交点なので,
\( y=-x+6 \) に \( x=-2 \) を代入すると,
\( y=-(-2)+6=8 \)
よって,点 \( Q \) の座標は \( (-2,8) \) になります。
(2) 【会話Ⅱ】の ➄ , ⑥ に当てはまる数をそれぞれ求めなさい。
【解答】
➄ ・・・ \( 15 \)
⑥ ・・・ \( t=\dfrac{3}{2} \)
【解説】
➄
\( △APB \) を \( △APQ \) と \( △BPQ \) にわけると,
\( t=0 \) のとき,点 \( Q \) の座標は \( Q(0,6) \) なので,
線分 \( PQ \) を底辺と考えると,
\( △APQ=6 \times 3 \times \dfrac{1}{2}=9 \)
\( △BPQ=6 \times 2 \times \dfrac{1}{2}=6 \)
なので,
\( △APB=△APQ+△BPQ=15 \)
⑥
点 \( R \) の \( y \) 座標は \( 0 \) なので,点 \( P \) が線分 \( QR \) の中点になるとき,
点 \( Q \) の \( y \) 座標の値は,点 \( P \) の \( y \) 座標の値の2倍になります。
点 \( P \) は \( y=x^2 \) 上の点なので,
\( x=t \) のときの \( y \) 座標は \( t^2 \) と表せます。
点 \( Q \) は \( y=-x+6 \) 上の点なので,
\( x=t \) のときの \( y \) 座標は \( -t+6 \) と表せます。
ここから,
\( -t+6=2t^2 \)
\( 2t^2+t-6=0 \)
\( (2t-3)(t+2)=0 \)
\( t=-2,\dfrac{3}{2} \)
求めるのは,\( t=-2 \) ではない方なので,あてはまる \( t \) の値は,\( t=\dfrac{3}{2} \) になります。
(3) \( △APB \) について,正しく述べているものを,次のア~オからすべて選び,記号で答えなさい。
ア \( t=0 \) のとき,\( △APB \) は \( ∠B=90° \) の直角三角形である。
イ \( t=0 \) のとき,\( △APB \) の面積は,\( y \) 軸によって二等分される。
ウ \( t=-1 \) と \( t=0 \) のときの \( △APB \) の面積は等しい。
エ 点 \( P \) が線分 \( QR \) の中点になるとき,\( △APB \) の面積は,\( △ARB \) の面積の \( \dfrac{1}{2} \) 倍である。
オ \( t \) の値が変わると,\( △APB \) の3つの辺は,すべて長さが変わる。
【解答】
ウ \( t=-1 \) と \( t=0 \) のときの \( △APB \) の面積は等しい。
エ 点 \( P \) が線分 \( QR \) の中点になるとき,\( △APB \) の面積は,\( △ARB \) の面積の \( \dfrac{1}{2} \) 倍である。
【解説】
【正しいといえる理由】
ウ \( t=-1 \) と \( t=0 \) のときの \( △APB \) の面積は等しい。
\( t=0 \) のときの点 \( P \) を点 \( P’ \) と名前をつけ直して区別すると,
等積変形の考え方から \( △APB \) と \( △AP’B \) の面積は等しいといえます。
\( t=-1 \) のときの点 \( P \) の座標は \( P(-1,1) \)
\( t=0 \) のときの点 \( P’ \) の座標は \( P’(0,0) \)
なので,直線 \( PP’ \) の傾きは \( \dfrac{0-1}{0-(-1)}=-1 \)
直線 \( AB \) と直線 \( PP’ \) の傾きは等しいので,
2直線は平行になっています。
よって,等積変形の考え方から,\( △APB \) と \( △AP’B \) の面積は等しくなっています。
エ 点 \( P \) が線分 \( QR \) の中点になるとき,\( △APB \) の面積は,\( △ARB \) の面積の \( \dfrac{1}{2} \) 倍である。
\( △APB \) を \( △APQ \) と \( △BPQ \) に,\( △ARB \) を \( △ARQ \) と \( △BRQ \) にわけます。
線分 \( PQ,RQ \) を底辺とすると,\( PQ=RP \) より \( 2PQ=RQ \) であり,
\( △APQ \) と \( △ARQ \),\( △BPQ \) と \( △BRQ \) はそれぞれ高さが共通なので,
\( 2△APQ=△ARQ \)
\( 2△BPQ=△BRQ \)
となっています。
このとき,\( △APB=△APQ+△BPQ \) であることから,
\( △ARB=△ARQ+△BRQ \)
\( =2△APQ+2△BPQ \)
\( =2(△APQ+△BPQ) \)
\( =2△APB \)
つまり,\( △APB=\dfrac{1}{2}△ARB \) になっています。
【正しくない理由】
ア \( t=0 \) のとき,\( △APB \) は \( ∠B=90° \) の直角三角形である。
直線 \( AB \) の傾きは \( -1 \),直線 \( PB \) の傾きは \( 2 \) であり,
2直線の傾きの積が \( -1 \) ではないので,\( ∠B=90° \) ではありません。
垂直に交わる2直線の傾きの積は \( -1 \) になります。
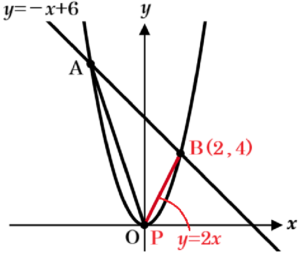
直線 \( PB \) は \( P(0,0),B(2,4) \) を通るので,
傾きは \( \dfrac{4-0}{2-0}=2 \) になっています。
直線 \( AB \) の傾きは \( -1 \) であり,
2直線の傾きの積は \( -1 \times 2=-2 \) なので,
\( ∠B=90° \) ではありません。
イ \( t=0 \) のとき,\( △APB \) の面積は,\( y \) 軸によって二等分される。
2より,\( t=0 \) のとき,\( △APQ=9,△BPQ=6 \) なので,二等分されていません。
オ \( t \) の値が変わると,\( △APB \) の3つの辺は,すべて長さが変わる。
\( t \) の値を変えても2点 \( A,B \) の位置は変わらないので,辺 \( AB \) の長さは変わりません。
大問5
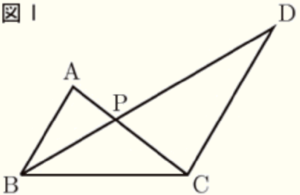
図Ⅰは,\( △ABC \) において,\( AB//DC \),
\( BC=CD \) となる点 \( D \) をとり,線分 \( DB \) を
ひいたものである。また,線分 \( AC \) と線分 \( DB \)
の交点を \( P \) とする。
このとき,次の1~3の問いに答えなさい。
1 \( ∠BCD=110° \) のとき,\( ∠ABD \) の大きさを求めなさい。
【解説】
\( BC=CD \) より,
\( △BCD \) は二等辺三角形なので,
\( ∠CDB=∠CBD=\dfrac{180°-110°}{2} \)
\( =35° \)
\( AB//DC \) より,錯角は等しいので,
\( ∠ABD=∠CDB=35° \)
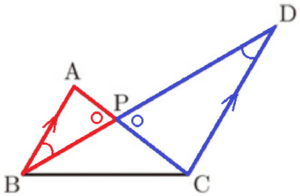
2 \( △APB \) ∽ \( △CPD \) であることを証明しなさい。
【解答】
\( △APB \) と \( △CPD \) において,
対頂角は等しいので,
\( ∠APB=∠CPD \) ・・・ ➀
\( AB//DC \) より,錯角は等しいので,
\( ∠PBA=∠PDC \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △APB \) ∽ \( △CPD \)
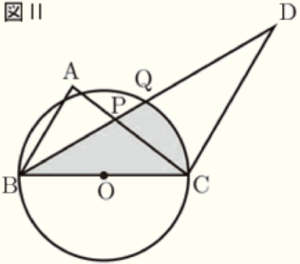
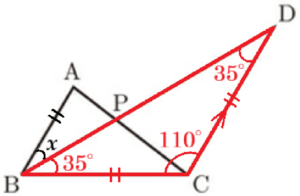
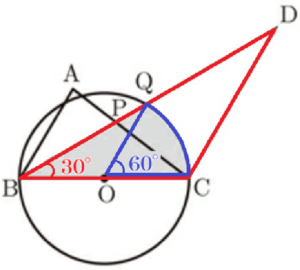
3 図Ⅱは,図Ⅰに線分 \( BC \) を直径とする円 \( O \) をかき,円 \( O \) と線分 \( BD \) との交点を \( Q \) としたものである。
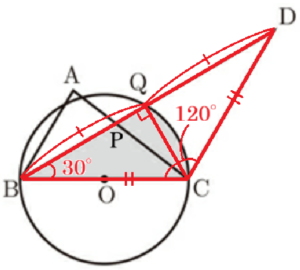
\( AB:CD=3:5,∠BCD=120° \) のとき,次の(1),(2)の問いに答えなさい。
(1) \( BP:PQ \) を求めなさい。
【解説】
\( △BCD \) において,\( BC=CD,∠BCD=120° \) より,
\( ∠CBD=∠CDB=\dfrac{180°-120°}{2} \)
\( =30° \)
補助線 \( CQ \) をひくと,\( ∠BQC \) は直径 \( BC \) に
対する円周角であり,\( ∠BQC=90° \) です。
ここから,線分 \( CQ \) は,二等辺三角形の頂角から向かい合う辺 \( BD \) にひいた垂線なので,
交点 \( Q \) は線分 \( BD \) の中点になっています。
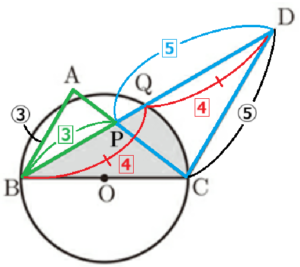
また,2より \( △APB \) ∽ \( △CPD \) であり,
\( AB:CD=3:5 \) より対応する辺は等しいので,
\( BP:DP=3:5 \)
点 \( Q \) は線分 \( BD \) の中点であることから,
\( BQ:DQ=1:1=4:4 \)
とすると,
\( BP:PQ=BP:(BQ-BP) \)
\( =3:(4-3) \)
\( =3:1 \)
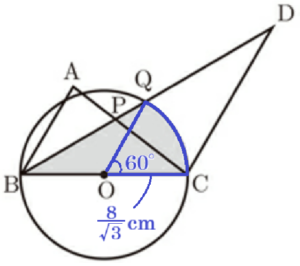
(2) \( PQ=2 \; cm \) のとき,\( BQ,BC \) と \( \stackrel{\huge\frown}{ QC } \) で囲まれた部分( ) の面積を求めなさい。
ただし,円周率は \( \pi{} \) とする。
【解答】
\( \left( \dfrac{16\sqrt{3}}{3}+\dfrac{32\pi{}}{9} \right) \; cm^2 \)
【解説】
補助線 \( OQ \) をひいて,\( △OBQ \) とおうぎ形 \( OCQ \) にわけて面積を求めます。
【おうぎ形 \( OCQ \) の面積を求める】
おうぎ形の面積を求めるために,まず半径と中心角を求めます。
STEP1 中心角を求める
\( ∠CBD \) は \( \stackrel{\huge\frown}{ QC } \) に対する円周角,
\( ∠COQ \) は \( \stackrel{\huge\frown}{ QC } \) に対する中心角
なので,
\( ∠COQ=2∠CBD=60° \)
\( \phantom{ } \)
STEP2 半径を求める
\( △BQC \) は \( 30°,60°,90° \) の直角三角形,
(1)より,\( BP:PQ=3:1 \) なので,
\( CQ=\dfrac{BQ}{\sqrt{3}} \)
\( =\dfrac{(BP+PQ)}{\sqrt{3}} \)
\( =\dfrac{8}{\sqrt{3}} \; (cm) \)
\( △OCQ \) は,\( ∠OCQ=60° \) の二等辺三角形
であり,正三角形なので,円 \( O \) の半径は \( \dfrac{8}{\sqrt{3}} \; cm \) です。
\( \phantom{ } \)
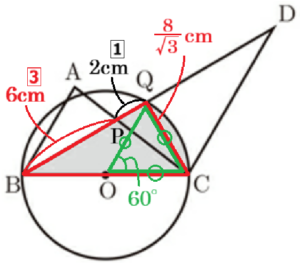
STEP3 おうぎ形の面積を求める
おうぎ形 \( OCQ \) は,半径 \( \dfrac{8}{\sqrt{3}} \; cm \),中心角 \( 60° \)
なので,面積は
\( \pi{} \times \left(\dfrac{8}{\sqrt{3}} \right)^2 \times \dfrac{60°}{360°}=\dfrac{32\pi{}}{9} \; (cm^2) \)
\( \phantom{ } \)
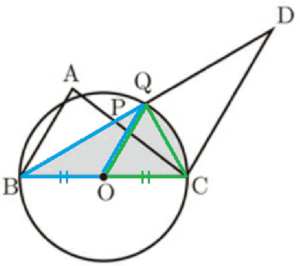
【 \( △OBQ \) の面積を求める】
\( △OBQ \) の面積をより簡単に求めるために,まず,\( △OBQ \) と \( △BQC \) の面積比を求めます。
STEP1 \( △OBQ \) と \( △BQC \) の面積比を求める
\( △OBQ \) の底辺を線分 \( OB \),
\( △OQC \) の底辺を線分 \( OC \) とすると,
\( OB=OC \) で,高さが共通なので,
\( △OBQ \) と \( △OCQ \) の面積は等しくなります。
\( △BQC=△OBQ+△OCQ \) であることから,
\( △OBQ \) の面積は \( △BQC \) の面積の半分に
なっています。
\( \phantom{ } \)
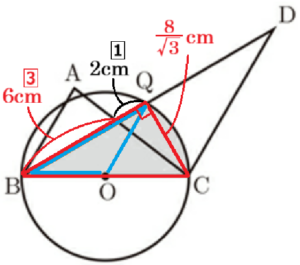
STEP2 \( △OBQ \) の面積を求める
\( △BQC \) の底辺を \( BQ \),高さを \( CQ \) とすると,
\( △OBQ=\dfrac{1}{2}△BQC \)
\( =\dfrac{1}{2} \times \left\{ (6+2) \times \dfrac{8}{\sqrt{3}} \times \dfrac{1}{2} \right\} \)
\( =\dfrac{16}{\sqrt{3}} \)
\( =\dfrac{16\sqrt{3}}{3} \; (cm^2) \)
\( \phantom{ } \)
以上より,求める面積は \( \left( \dfrac{16\sqrt{3}}{3}+\dfrac{32\pi{}}{9} \right) \; cm^2 \) になります。


![]()
 だね。\( 20=4 \times 5 \) の \( 5 \) は,どこかに隠れていないかな。
だね。\( 20=4 \times 5 \) の \( 5 \) は,どこかに隠れていないかな。 をみて! \( 5 \) は左上の数 \( 1 \) と右下の数 \( 9 \) の和の半分になっているよね。
をみて! \( 5 \) は左上の数 \( 1 \) と右下の数 \( 9 \) の和の半分になっているよね。 と表されるから,
と表されるから,