A
大問1
(1) \( 1+2 \times (-3)^2 \) を計算せよ。
【解説】
\( =1+2 \times 9 \)
\( =1+18 \)
\( =19 \)
(2) \( 2250 \) 円の商品を \( 10 \; \% \) 引きで1つ購入するとき,支払う金額はいくらか。ただし,消費税は考えないものとする。
【解説】
\( 10 \; \% \) 引きで商品を購入するということは,
もとの値段の \( 90 \; \% \) の値段で購入するということです。
\( 90 \; \% \) を小数で表すと \( 0.9 \) なので,
\( 2250 \times 0.9=2025 \)(円)
(3) \( \sqrt{18}-\sqrt{8} \) を計算せよ。
【解説】
\( =3\sqrt{2}-2\sqrt{2} \)
\( =\sqrt{2} \)
(4) \( y \) は \( x \) に反比例し,\( x=3 \) のとき,\( y=5 \) である。このとき,\( y \) を \( x \) の式で表せ。
【解答】
\( y=\dfrac{15}{x} \)
【解説】
反比例を表す式は \( y=\dfrac{a}{x} \)( \( a \) は定数)です。
この式に \( x=3,y=5 \) を代入すると,
\( 5=\dfrac{a}{3} \)
\( a=15 \)
よって,求める式は \( y=\dfrac{15}{x} \)
(5) 連立方程式 \( \left\{ \begin{array}{}
2x+y=4 \\
3x-2y=-1 \\
\end{array} \right. \) を解け。
【解説】
\( \left\{ \begin{array}{}
2x+y=4 \;\; ・・・ \;\; ➀ \\
3x-2y=-1 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( \times 2 \) すると,
\( 4x+2y=8 \) ・・・ ➀’
➀’\( + \) ➁ すると,
\( 7x=7 \)
\( x=1 \)
➀ に代入すると,
\( 2 \times 1+y=4 \)
\( 2+y=4 \)
\( y=2 \)
(6) \( a^2-5a+6 \) を因数分解せよ。
(7) 2次方程式 \( x^2+3x+1=0 \) を解け。
【解答】
\( x=\dfrac{-3±\sqrt{5}}{2} \)
【解説】
解の公式より,
\( x=\dfrac{-3±\sqrt{3^2-4 \times 1 \times 1}}{2 \times 1} \)
\( =\dfrac{-3±\sqrt{9-4}}{2} \)
\( =\dfrac{-3±\sqrt{5}}{2} \)
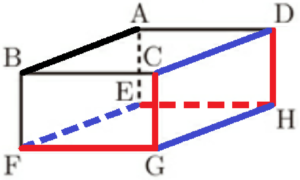
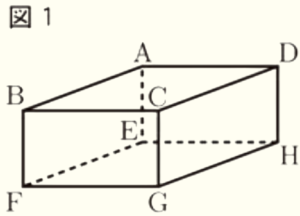
(8) 図1の直方体において,辺 \( AB \) とねじれの位置にある辺の本数は何本か。
【解説】
ねじれの位置にある辺とは,どこまでのばしても交わらない辺のうち,平行ではないもののことです。
辺 \( AB \) と交わらない辺は \( CD,CG,DH,EF,EH,FG,GH \) であり,
ここから辺 \( AB \) と平行な辺 \( CD,EF,GH \) を除いた
辺 \( CG,DH,EH,FG \) の4本がねじれの位置にある辺になります。
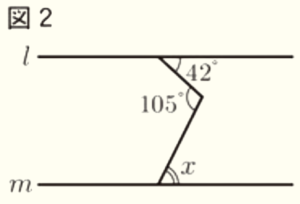
(9) 図2において,\( l//m \) のとき,\( ∠x \) の大きさは何度か。
【解説】
右の図のように直線 \( l,m \) と平行な直線をひくと,
\( 105° \) の角は \( 42° \) と \( 63° \) に分かれるので,
錯角は等しく,\( ∠x=63° \)
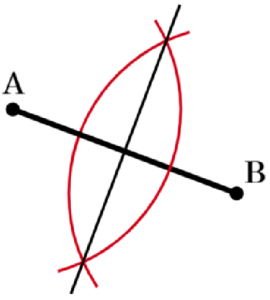
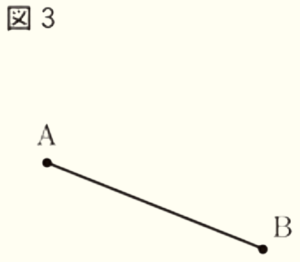
(10) 図3において,線分 \( AB \) の垂直二等分線を定規とコンパスを用いて作図せよ。ただし,作図に用いた線は消さずに残しておくこと。
大問2
問1 図1は,N市の1973年8月と2023年8月の日ごとの最高気温をそれぞれ31日分調べ,その分布のようすを箱ひげ図に表したものである。
このとき,次の(1),(2)に答えよ。
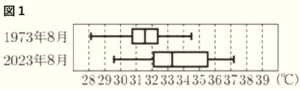
(1) 次の➀~➃について,図1から読み取れることとして必ず正しいと判断できるものを1つ選び,その番号を書け。
➀ 1973年8月は,最高気温が \( 32.0^\circ C \) の日が1日はある。
➁ 1973年8月の四分位範囲は,\( 3.0^\circ C \) より大きい。
➂ 1973年8月の第1四分位数は,2023年8月の第3四分位数より大きい。
➃ 2023年8月は,最高気温が \( 35.0^\circ C \) より高い日が8日以上ある。
【解答】
➃ 2023年8月は,最高気温が \( 35.0^\circ C \) より高い日が8日以上ある。
【解説】
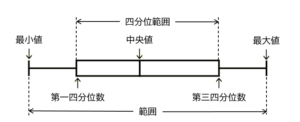
➀ ・・・ 箱ひげ図のデータからだけでは判断できません。
➁ ・・・ 四分位範囲は「第3四分位数 \( – \) 第1四分位数」で求めることができます。
1973年8月の第1四分位数は,\( 30.7^\circ C \),第3四分位数は,\( 32.3^\circ C \) なので,
四分位数は,\( 32.3-30.7=1.6 \; (^\circ C) \) になります。
➂ ・・・1973年8月の第1四分位数は \( 31.0^\circ C \) 未満,2023年8月の第3四分位数は \( 35.0^\circ C \) 以上
なので,2023年8月の第3四分位数の方が大きくなっています。
➃ ・・・ 31日分のデータを集計しているので,第3四分位数は気温の高い方から8番目の値になります。
2023年8月の第3四分位数は \( 35.0^\circ C \) より大きいので,最高気温が \( 35.0^\circ C \) より高い日が
8日以上あるといえます。
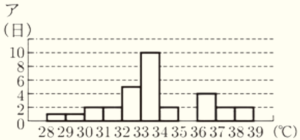
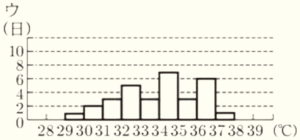
(2) N市の2023年8月の日ごとの最高気温を表しているヒストグラムと考えられるものを,
次のア~ウの中から1つ選び,その記号を書け。
【解説】
箱ひげ図から最小値は \( 29.0^\circ C \) 以上 \( 30.0^\circ C \) 未満なので,
\( 28.0^\circ C \) 以上 \( 29.0^\circ C \) 未満の階級の度数が1になっているアのヒストグラムはあてはまりません。
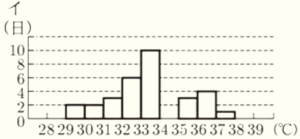
この箱ひげ図は,31日分のデータを集計しているので,中央値は気温の低い方から16番目の値になります。
中央値は \( 33.0^\circ C \) 以上 \( 34.0^\circ C \) 未満であり,
ヒストグラムで16番目の値が \( 33.0^\circ C \) 以上 \( 34.0^\circ C \) 未満の階級にあるのはイになります。
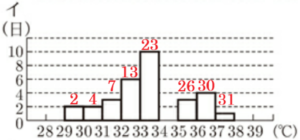
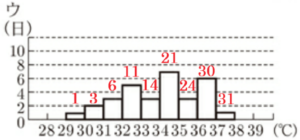
イとウのヒストグラムに累積度数を書き込むと次のようになり,
イのヒストグラムでは,気温の低い方から16番目の値は \( 33.0^\circ C \) 以上 \( 34.0^\circ C \) 未満の階級,
ウのヒストグラムでは,気温の低い方から16番目の値は \( 34.0^\circ C \) 以上 \( 35.0^\circ C \) 未満の階級
に含まれていることがわかります。
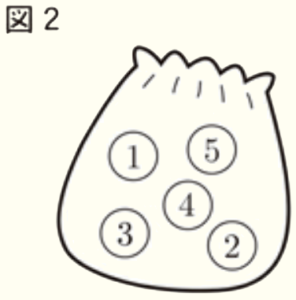
問2 図2のように,袋に1から5までの数字が1つずつ書かれた同じ大きさの球が5個入っている。この袋の中の球をよくかきまぜて1個取り出し,取り出した球に書かれている数を確認した後,袋に戻す。これを2回行い,1回目に取り出した球に書かれている数を \( x \),2回目に取り出した球に書かれている数を \( y \) とする。
このとき,次の(1)~(3)に答えよ。
(1) 球の取り出し方は全部で何通りあるか。
【解説】
1回目の球の取り出し方,2回目の球の取り出し方は,どちらも5通りずつなので,
全部で \( 5 \times 5=25 \)(通り)になります。
(2) \( x+y=5 \) となる確率を求めよ。
【解説】
\( x+y=5 \) となるのは,
\( (x,y)=(1,4),(2,3),(3,2),(4,1) \)
の4通りなので,確率は \( \dfrac{4}{25} \)
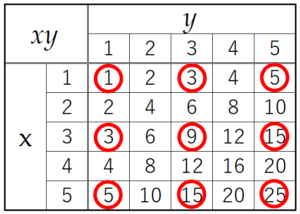
(3) \( x \) と \( y \) の積 \( xy \) の値が奇数となる確率を求めよ。
【解説】
\( x \) と \( y \) の組み合わせと \( xy \) の値を表に書き出すと,あてはまる組み合わせは9通りなので,
確率は \( \dfrac{9}{25} \)
【別解】
整数どうしの積が奇数になるのは,奇数 \( \times \) 奇数 の場合だけです。
\( x \) と \( y \) がどちらも奇数になる組み合わせは,
\( (x,y)=(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5) \)
の9通りなので,確率は \( \dfrac{9}{25} \)
(参考)
整数どうしの積の組み合わせは次のとおりです。
偶数 \( \times \) 偶数 \( = \) 偶数
偶数 \( \times \) 奇数 \( = \) 偶数
奇数 \( \times \) 偶数 \( = \) 偶数
奇数 \( \times \) 奇数 \( = \) 奇数
問3 「連続する4つの整数を小さい方から順に \( a,b,c,d \) とするとき,\( bc-ad \) の値はいつでも \( 2 \) になる」ことを文字 \( a \) を使って証明せよ。ただし,証明は「\( b,c,d \) をそれぞれ \( a \) を用いて表すと,」に続けて完成させること。
【解答】
\( b,c,d \) をそれぞれ \( a \) を用いて表すと,
\( b=a+1,c=a+2,d=a+3 \) となるので,
\( bc-ad=(a+1)(a+2)-a(a+3) \)
\( =(a^2+3a+2)-(a^2+3a) \)
\( =2 \)
よって,
連続する4つの整数を小さい方から順に \( a,b,c,d \) とするとき,
\( bc-ad \) の値はいつでも \( 2 \) になる
大問3
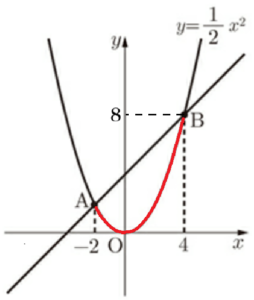
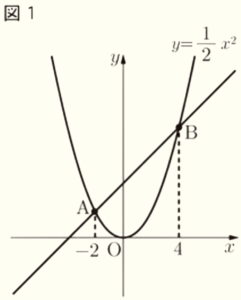
図1,図2のように,関数 \( y=\dfrac{1}{2}x^2 \) のグラフ上に2点 \( A,B \) があり,\( x \) 座標はそれぞれ \( -2,4 \) である。原点を \( O \) として,次の問いに答えなさい。
問1 点 \( B \) の \( y \) 座標を求めよ。
【解説】
点 \( B \) は \( y=\dfrac{1}{2}x^2 \) 上の点で,
\( x \) 座標が \( 4 \) なので,\( y \) 座標の値は,
\( y=\dfrac{1}{2} \times 4^2=8 \)
問2 関数 \( y=\dfrac{1}{2}x^2 \) について,\( x \) の変域が \( -2≦x≦4 \) のときの \( y \) の変域を求めよ。
【解説】
関数 \( y=ax^2 \; (a>0) \) について,
\( x \) の変域が \( 0 \) を含むとき,
\( y \) の最小値は \( 0 \) になります。
また,\( x \) の絶対値が最も大きくなるとき,
\( y \) の値は最大値をとります。
\( x \) の変域が \( -2≦x≦4 \) なので,
\( y \) の最小値は \( 0 \),
\( x \) の絶対値が最も大きくなるのは \( x=4 \) のとき
なので,
\( y=\dfrac{1}{2} \times 4^2=8 \)
よって,\( y \) の変域は,\( 0≦y≦8 \) になります。
問3 直線 \( AB \) の式を求めよ。
【解説】
点 \( A \) は \( y=\dfrac{1}{2}x^2 \) 上の点で,
\( x \) 座標が \( -2 \) なので,\( y \) 座標の値は,
\( y=\dfrac{1}{2} \times (-2)^2=2 \)
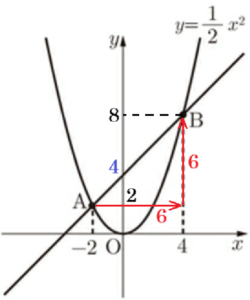
直線 \( AB \) の式を \( y=mx+n \) とすると,
\( A(-2,2),B(4,8) \) を通るので,
\( m=\dfrac{8-2}{4-(-2)}=1 \)
\( y=x+n \) に \( x=4,y=8 \) を代入すると,
\( 8=4+n \)
\( n=4 \)
よって,直線 \( AB \) の式は \( y=x+4 \) になります。
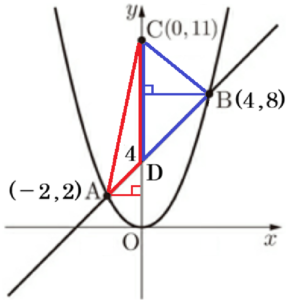
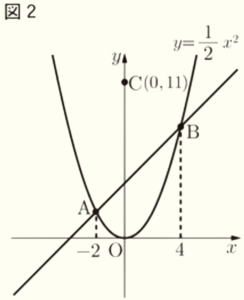
問4 図2のように,\( y \) 軸上に点 \( C(0,11) \) をとる。このとき,次の(1),(2)に答えよ。
(1) \( △ABC \) の面積を求めよ。
【解説】
直線 \( AB \) と \( y \) 軸の交点を \( D \) とすると,
\( △ABC \) は \( △ACD \) と \( △BCD \) にわけることができます。
\( △ACD \) と \( △BCD \) において,線分 \( CD \) を底辺とすると,
\( △ACD=7 \times 2 \times \dfrac{1}{2}=7 \)
\( △BCD=7 \times 4 \times \dfrac{1}{2}=14 \)
であり,
\( △ABC=7+14=21 \)
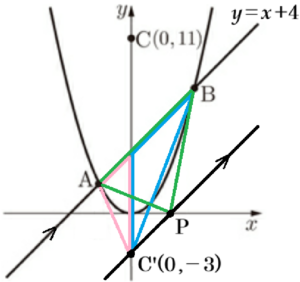
(2) \( x \) 軸上に点 \( P \) をとる。\( △ABC \) の面積と \( △ABP \) の面積が等しくなるとき,点 \( P \) の \( x \) 座標をすべて求めよ。
【解説】
あてはまる点 \( P \) は,直線 \( AB \) より左側にあるときと右側にあるときの2つあるので,
それぞれ考えていきます。
● 点 \( P \) が直線 \( AB \) の左側にあるとき
\( △ABC \) と \( △ABP \) は辺 \( AB \) が共通なので,等積変形の考え方から,
点 \( P \) が点 \( C \) を通り,直線 \( AB \) と平行な直線(直線 \( n \) とします)上にあるとき,
\( △ABC \) の面積と \( △ABP \) の面積が等しくなります。

直線 \( n \) と直線 \( AB \) は傾きが等しいので,傾きは \( 1 \),
点 \( C \) を通るので,\( y \) 切片は \( 11 \)
よって,直線 \( n \) の式は \( y=x+11 \)
点 \( P \) は,直線 \( n \) と \( x \) 軸の交点なので,\( y=0 \) を代入すると,
\( 0=x+11 \)
\( x=-11 \)
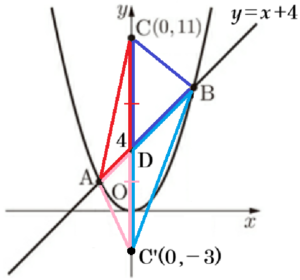
● 点 \( P \) が直線 \( AB \) の右側にあるとき
左側にあるときと同じように等積変形の考え方を使いますが,
準備として,\( △ABC \) の面積と \( △ABC’ \) の面積が等しくなるような
\( y \) 軸上の点 \( C’ \) の座標を求めます。
\( △ABC’ \) を \( △AC’D \) と \( △BC’D \) にわけ,
線分 \( C’D \) を底辺とすると,
\( △ACD \) と \( △AC’D \),\( △BCD \) と \( △BC’D \) は,それぞれ高さが等しいので,
\( C’D=CD=7 \) のとき,\( △ACD=△AC’D,△BCD=△BC’D \) となり,
\( △ABC=△ABC’ \) になります。
このとき,点 \( D \) の \( y \) 座標が \( 4 \) であることから,点 \( C’ \) の \( y \) 座標は \( -3 \) なので,
点 \( C’ \) の座標は \( C'(0,-3) \) になります。
ここから,\( △ABP=△ABC’ \) であるとき,\( △ABC=△ABP \) になります。
\( △ABC’ \) と \( △ABP \) は辺 \( AB \) が共通なので,
等積変形の考え方から,
点 \( P \) が点 \( C \) を通り,直線 \( AB \) と平行な直線
(直線 \( m \) とします)上にあるとき,
\( △ABC’ \) の面積と \( △ABP \) の面積が等しくなります。
直線 \( m \) と直線 \( AB \) は傾きが等しいので,
傾きは \( 1 \),
点 \( C’ \) を通るので,\( y \) 切片は \( -3 \)
よって,直線 \( m \) の式は \( y=x-3 \)
点 \( P \) は,直線 \( m \) と \( x \) 軸の交点なので,\( y=0 \) を代入すると,
\( 0=x-3 \)
\( x=3 \)
大問4
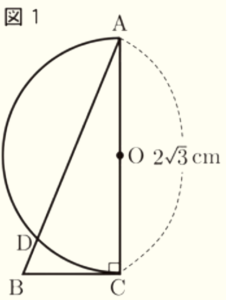
図1~図3のように,\( AC=2\sqrt{3} \; cm \),\( ∠ACB=90° \) の直角三角形 \( ABC \) がある。また,点 \( O \) を中心とし辺 \( AC \) を直径とする半円がある。半円と辺 \( AB \) は交わり,その交点を \( D \) とする。
このとき,次の問いに答えなさい。
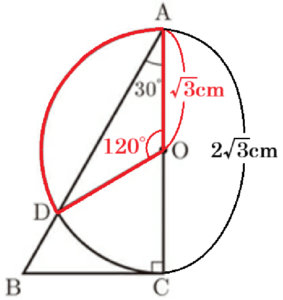
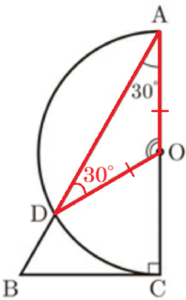
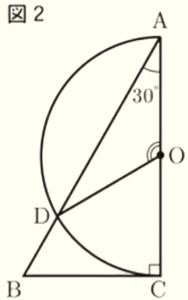
問1 図2のように,\( ∠BAC=30° \) とする。
このとき,次の(1),(2)に答えよ。
(1) \( ∠AOD \) の大きさは何度か。
【解説】
\( △AOD \) は \( OA=OD \) の二等辺三角形
なので,\( ∠ADO=∠BAC=30° \) であり,
\( ∠AOD=\dfrac{180°-30° \times 2}{2}=120° \)
(2) おうぎ形 \( AOD \) の面積は何 \( cm^2 \) か。
【解説】
\( AC=2\sqrt{3} \; cm \) は半円の直径なので,
半径 \( OA=\sqrt{3} \; cm \) になります。
(1)より,おうぎ形 \( AOD \) の中心角は
\( ∠AOD=120° \) なので,
おうぎ形 \( AOD \) の面積は
\( \pi{} \times (\sqrt{3})^2 \times \dfrac{120°}{360°}=\pi{} \; (cm^2) \)
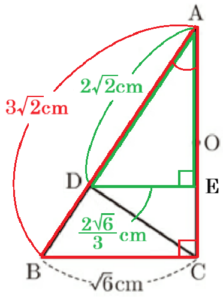
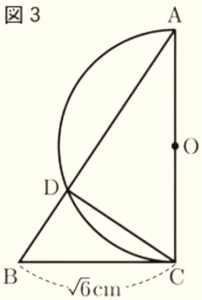
問2 図3のように,\( BC=\sqrt{6} \; cm \) とする。
このとき,次の(1)~(3)に答えよ。
(1) \( △ABC \) ∽ \( △ACD \) であることを証明せよ。
【解答】
\( △ABC \) と \( △ACD \) において,
共通な角なので,
\( ∠BAC=∠CAD \) ・・・ ➀
仮定より \( ∠ACB=90° \) ・・・ ➁
直径に対する円周角なので,
\( ∠ADC=90° \) ・・・ ➂
➁➂より,
\( ∠ACB=∠ADC \) ・・・ ➃
➀➃より,2組の角がそれぞれ等しいので,
\( △ABC \) ∽ \( △ACD \)
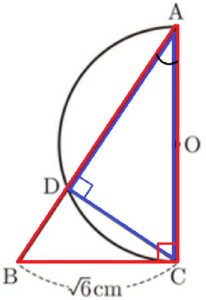
(2) 線分 \( AD \) の長さは何 \( cm \) か。
【解答】
\( AD=2\sqrt{2} \; cm \)
【解説】
\( △ABC \) において,三平方の定理より,
\( AB^2=(2\sqrt{3})^2+(\sqrt{6})^2=18 \)
\( AB=3\sqrt{2} \; (cm) \)( \( AB>0 \) より)
(1)より,\( △ABC \) ∽ \( △ACD \) なので,
\( AD=x \; cm \) とすると,
\( AC:AD=AB:AC \)
\( 2\sqrt{3}:x=3\sqrt{2}:2\sqrt{3} \)
\( 3\sqrt{2}x=12 \)
\( x=2\sqrt{2} \; (cm) \)
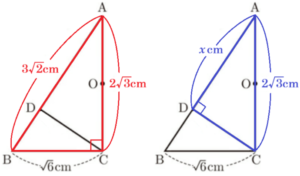
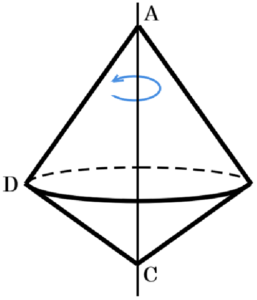
(3) \( △ADC \) を,辺 \( AC \) を軸として1回転させてできる立体の体積は何 \( cm^3 \) か。
【解答】
\( \dfrac{16\sqrt{3}}{9}\pi{} \; cm^3 \)
【解説】
\( △ADC \) を,辺 \( AC \) を軸として1回転させてできる立体は右の図のように円すいを2つくっつけた形になっています。
\( △ADC \) において,点 \( D \) から線分 \( AC \) に垂線をひいた交点を \( E \) とすると,
\( △ABC \) ∽ \( △ADE \) になります。
\( AB=3\sqrt{2} \; cm,AD=2\sqrt{2} \; cm \) なので,
\( BC:DE=AB:AD \)
\( \sqrt{6}:DE=3\sqrt{2}:2\sqrt{2} \)
\( \sqrt{6}:DE=3:2 \)
\( DE=\dfrac{2\sqrt{6}}{3} \; (cm) \)
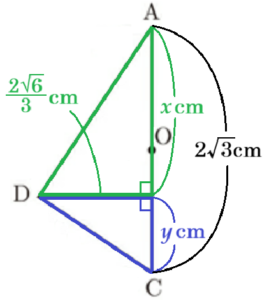
線分 \( DE \) は2つの円すいの底面の半径なので,
\( AE=x \; cm,CE=y \; cm \) とすると,
上側の円すいの体積は
\( \left\{ \pi{} \times \left( \dfrac{2\sqrt{6}}{3} \right)^2 \right\} \times x \times \dfrac{1}{3}=\dfrac{8}{9}\pi{}x \; (cm^3) \)
下側の円すいの体積は
\( \left\{ \pi{} \times \left( \dfrac{2\sqrt{6}}{3} \right)^2 \right\} \times y \times \dfrac{1}{3}=\dfrac{8}{9}\pi{}y \; (cm^3) \)
と表すことができるので,求める立体の体積は
\( \dfrac{8}{9}\pi{}x+\dfrac{8}{9}\pi{}y=\dfrac{8}{9}\pi{}(x+y) \; (cm^3) \)
と表すことができます。
ここで,\( AC=2\sqrt{3} \; cm \) より,\( x+y=2\sqrt{3} \) を代入すると,
\( \dfrac{8}{9}\pi{}(x+y)=\dfrac{8}{9}\pi{} \times 2\sqrt{3}=\dfrac{16\sqrt{3}}{9}\pi{} \; (cm^3) \)
になります。
大問5
花子さんと太郎さんは,先生といっしょにミツバチの巣の 画像 を見て,ミツバチの巣の穴の形について話をしている。以下は,その中の会話の一部である。[場面1],[場面2]を読んで,あとの問いに答えなさい。
[場面1]
花子:似たような形の穴がたくさんあいているね。
太郎:1つ1つの穴の形は,正六角形に見えるよね。
先生:そうですね。ミツバチの巣は,複数の正六角柱の筒がすき間なく並んでいるような構造を
しているのですよ。
花子:だから,1つ1つの穴の形は正六角形に見えるのですね。でも,正三角柱や正四角柱でも
すき間なく並べることができそうですよね。
太郎:正五角柱でもすき間なく並べることができるのではないかな。少し考えてみようよ。
\( \phantom{ } \)
(数分後)
\( \phantom{ } \)
花子:私は,穴の形に着目して【メモ】のように考えてみました。
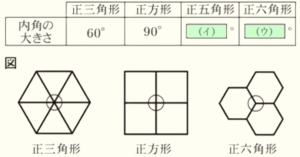
【メモ】
下の図のように,1種類の合同な正多角形をすき間なく重ならないように並べることができるのは,
1つの頂点に集まる内角の大きさの合計が
(ア) ° になるときである。
\( \phantom{ } \)
\( \phantom{ } \)
正三角形,正方形,正六角形は1つの頂点に集まる内角の大きさの合計が
(ア) ° になるから,すき間なく重ならないように並べることができる。正五角形は1つの頂点に集まる内角の大きさの合計が
(ア) ° になることはないので,すき間なく重ならないように並べることはできない。
先生:よく説明できましたね。実は,1種類の合同な正多角形で,すき間なく重ならないように
並べることができる図形は,正三角形と正方形と正六角形しかないのですよ。
問1 (ア) ~ (ウ) にあてはまる数を答えよ。ただし,同じ記号には同じ数が入る。
【解答】
(ア) ・・・ \( 360 \)
(イ) ・・・ \( 108 \)
(ウ) ・・・ \( 120 \)
【解説】
(イ)
右の図のように正五角形の対角線をひくと三角形を3つくっつけた形になっています。
ここから,正五角形の5つの内角の和は
\( 180° \times 3=540° \)
になります。
正五角形の5つの内角の大きさは等しいので,1つの角の大きさは
\( \dfrac{540°}{5}=108° \)
\( \phantom{ } \)

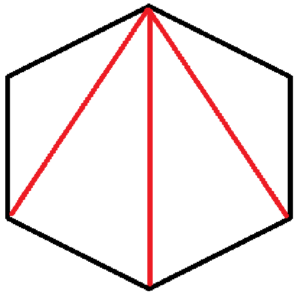
(ウ)
右の図のように正六角形の対角線をひくと三角形を4つくっつけた形になっています。
ここから,正六角形の6つの内角の和は
\( 180° \times 4=720° \)
になります。
正六角形の6つの内角の大きさは等しいので,1つの角の大きさは
\( \dfrac{720°}{6}=120° \)
\( \phantom{ } \)
[場面2]
先生:正三角柱や正四角柱でもすき間なく並べることができるのに,なぜ正六角柱なのでしょうね。
花子:正六角柱が最も多くのハチミツを蓄えることができるからではないでしょうか。
太郎:私は,巣を作る材料が最も少なくてすむのが正六角柱なのではないかと考えます。
先生:それでは,先ほどの花子さんの考えと同じように穴の形に着目して平面で考えてみましょう。
針金を巣の材料と見立てて考えてみてはどうですか。
花子:私は,同じ量の材料で,できるだけ大きな穴の形を作ることを考えてみようかな。
同じ長さの針金を3本用意して,それぞれ針金1本を使って,正三角形,正方形,正六角形を作って
面積を比較してみます。
太郎:それでは,私は,ミツバチが入る穴の形をできるだけ少ない材料で作ることを考えてみようかな。
1匹のミツバチを円と考えて,その円をぴったり囲むことができる正三角形,正方形,正六角形を
それぞれ針金で作って,その周の長さを比較してみます。
先生:よい考えですね。まずは,花子さんの考えについて,針金の長さを \( 6 \; cm \) として,
花子さんのノートに書いてみてください。
【花子さんのノート1】
針金の長さを \( 6 \; cm \) とする。正三角形を作ると1辺の長さは (エ) \( cm \) となるので,
面積は (オ) \( cm^2 \) となる。同じように考えると,正方形の面積は (カ) \( cm^2 \)
となり,正六角形の面積は (キ) \( cm^2 \) となる。
この3つの図形の面積を比較すると,
(ク) \( < \) (ケ) \( < \) (コ)
となるので,面積が最大となる図形は (サ) とわかる。
先生:よくできましたね。それでは次に,針金の長さに関わらずいつでも同じことがいえるのかを
調べるために,文字 \( a \) を使って針金の長さを表して,【花子さんのノート1】と同じように
計算して比較することで,面積が最大となる図形を調べましょう。
そのとき,針金の長さは正三角形,正方形,正六角形のいずれの図形でも,折り曲げたときの
1辺の長さが(整数)\( \times a \; cm^2 \) となるように工夫して表しましょう。
(数分後)
【花子さんのノート2】
針金の長さを (シ) \( a \; cm \) とする。
(ス)
先生:よくできましたね。次は,この結果からミツバチの巣についてどのようなことがいえるか
考えてみてください。
花子:わかりました。
太郎:先生,私も自分の考えについてノートに書いてみます。周の長さを計算すると,どのような結果に
なるか楽しみです。
問2 (エ) ~ (コ) にあてはまる数を答えよ。
【解答】
(エ) ・・・ \( 2 \)
(オ) ・・・ \( \sqrt{3} \)
(カ) ・・・ \( \dfrac{9}{4} \)
(キ) ・・・ \( \dfrac{3\sqrt{3}}{2} \)
(ク) ・・・ \( \sqrt{3} \)
(ケ) ・・・ \( \dfrac{9}{4} \)
(コ) ・・・ \( \dfrac{3\sqrt{3}}{2} \)
【解説】
(エ)
\( 6 \; cm \) の針金を3等分するので,
1辺の長さは \( 2 \; cm \)
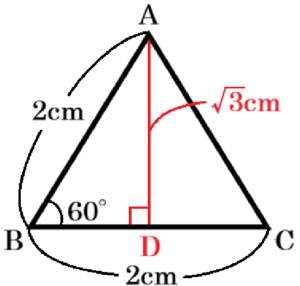
(オ)
正三角形 \( ABC \) において,点 \( A \) から辺 \( BC \) に垂線をひき,交点を \( D \) とすると,
\( △ABD \) は \( 30°,60°,90° \) の直角三角形なので,
\( AD=\dfrac{\sqrt{3}}{2} \times 2=\sqrt{3} \; (cm) \)
よって,正三角形 \( ABC \) の面積は,
\( 2 \times \sqrt{3} \times \dfrac{1}{2}=\sqrt{3} \; (cm^2) \)
\( \phantom{ } \)
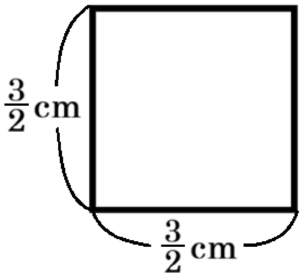
(カ)
1辺の長さは \( \dfrac{3}{2} \; cm \) なので,
この正方形の面積は,
\( \dfrac{3}{2} \times \dfrac{3}{2}=\dfrac{9}{4} \; (cm^2) \)
\( \phantom{ } \)
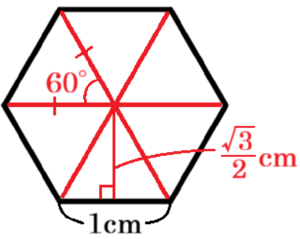
(キ)
1辺の長さは \( 1 \; cm \) であり,右の図のように対角線をひくと,1辺 \( 1 \; cm \) の正三角形が6個できます。
正三角形1個の面積は,
\( 1 \times \dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{4} \; (cm^2) \)
なので,正六角形の面積は,
\( \dfrac{\sqrt{3}}{4} \times 6=\dfrac{3\sqrt{3}}{2} \; (cm^2) \)
\( \phantom{ } \)
(ク) , (ケ) , (コ)
2つの数 \( a,b \) において,\( a<b \) であるとき,\( a^2<b^2 \) になります。
\( \sqrt{3},\dfrac{9}{4},\dfrac{3\sqrt{3}}{2} \) をそれぞれ2乗すると,
\( 3,\dfrac{81}{16}=5.0625,\dfrac{27}{4}=6.75 \) なので,
小さい順に並べると
\( \sqrt{3}<\dfrac{9}{4}<\dfrac{3\sqrt{3}}{2} \)
問3 (サ) にあてはまることばを,次の1~3の中から1つ選び,その番号を書け。
1 正三角形 2 正方形 3 正六角形
問4 [場面2]の下線部をもとに, (シ) にあてはまる数と (ス) にあてはまる説明を書き入れて【花子さんのノート2】を完成させよ。
【解答】
(シ) ・・・ \( 12 \)
(ス)
正三角形の1辺の長さは \( 4a \; cm \) なので,面積は \( 4\sqrt{3}a^2 \; cm^2 \)
正方形の1辺の長さは \( 3a \; cm \) なので,面積は \( 9a^2 \; cm^2 \)
正六角形の1辺の長さは \( 2a \; cm \) なので,面積は \( 6\sqrt{3}a^2 \; cm^2 \)
と表すことができる。
このとき,\( 4\sqrt{3}a^2<9a^2<6\sqrt{3}a^2 \) なので,
面積が最大となる図形は正六角形である。
【解説】
(シ)
針金の長さを \( n \times a \; cm \)(\( n \) は整数)とすると,
正三角形の1辺の長さは \( \dfrac{n}{3} \times a \; cm \),
正方形の1辺の長さは \( \dfrac{n}{4} \times a \; cm \),
正六角形の1辺の長さは \( \dfrac{n}{6} \times a \; cm \),
と表すことができます。
1辺の長さが(整数)\( \times a \; cm^2 \) となるためには,
\( n \) が \( 3,4,6 \) のすべてで割り切れる必要がある,
つまり,\( n \) が \( 3,4,6 \) の公倍数(\( 12 \) の倍数)であればよいことになります。
(ス)





 \( \phantom{ } \)
\( \phantom{ } \)