大問1
(1) \( -a \times (2ab)^2 \div \left( -\dfrac{2}{3}ab^2 \right) \) を計算しなさい。
【解説】
\( =-a \times (2ab)^2 \times \left( -\dfrac{3}{2ab^2} \right) \)
\( =\dfrac{-a \times (2ab)^2 \times (-3)}{2ab^2} \)
\( =\dfrac{-a \times 4a^2b^2 \times (-3)}{2ab^2} \)
\( =6a^2 \)
(2) \( \dfrac{6+\sqrt{8}}{\sqrt{2}}+(2-\sqrt{2})^2 \) を計算しなさい。
【解説】
\( =\dfrac{6+2\sqrt{2}}{\sqrt{2}}+6-4\sqrt{2} \)
\( =3\sqrt{2}+2+6-4\sqrt{2} \)
\( =8-\sqrt{2} \)
(3) \( a \) を \( 0 \) でない定数とする。\( x \) の二次方程式 \( ax^2+4x-7a-16=0 \) の一つの解が \( x=3 \) であるとき,\( a \) の値を求めなさい。また,この方程式のもう一つの解を求めなさい。
【解答】
\( a=2 \)
もう一つの解 ・・・ \( x=-5 \)
【解説】
\( x=3 \) が解であるということは,この二次方程式に \( x=3 \) を代入すると成り立つということなので,
\( x=3 \) を代入すると,
\( a \times 3^2+4 \times 3-7a-16=0 \)
\( 9a+12-7a-16=0 \)
\( 2a=4 \)
\( a=2 \)
この二次方程式に \( a=2 \) を代入すると,
\( 2x^2+4x-14-16=0 \)
\( x^2+2x-15=0 \)
\( (x-3)(x+5)=0 \)
\( x=3,-5 \)
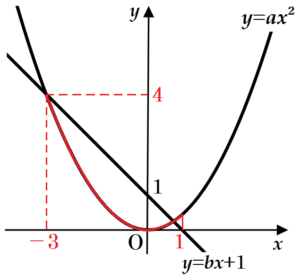
(4) \( a,b,c,d \) を定数とし,\( a>0,b<0,c<d \) とする。関数 \( y=ax^2 \) と関数 \( y=bx+1 \) について,\( x \) の変域が \( -3≦x≦1 \) のときの \( y \) の変域がともに \( c≦y≦d \) であるとき,\( a,b \) の値をそれぞれ求めなさい。
【解答】
\( a=\dfrac{4}{9},b=-1 \)
【解説】
\( a>0 \) より,\( y=ax^2 \) は下に凸の曲線であるとわかります。
また,\( x \) の変域は \( 0 \) を含んでいることから,
最小値は必ず \( 0 \) になるので,\( y \) の変域は \( 0≦y≦d \) となります。
\( b<0 \) より,\( y=bx+1 \) は右下がりの直線です。
\( x \) の変域が \( -3≦x≦1 \) のとき,
\( y \) の変域が \( 0≦y≦d \) なので,
\( x=1 \) のとき,\( y=0 \) になるとわかります。
また,切片が \( 1 \) なので,
この直線は \( (0,1),(1,0) \) を通り,
傾き \( b=-1 \) であるとわかります。
ここから,
\( y=-x+1 \) に \( x=-3 \) を代入すると,
\( y=-(-3)+1=4 \)
よって,\( y=ax^2 \) は,\( (-3,4) \) を通るので,
\( y=ax^2 \) に \( x=-3,y=4 \) を代入すると,
\( 4=a \times (-3)^2 \)
\( 9a=4 \)
\( a=\dfrac{4}{9} \)
(5) \( n \) を自然数とする。\( n≦\sqrt{x}≦n+1 \) を満たす自然数 \( x \) の個数が \( 100 \) であるときの \( n \) の値を求めなさい。
【解説】
\( n≦\sqrt{x}≦n+1 \) の各辺を2乗すると,\( n^2≦x≦(n+1)^2 \)
これを満たす自然数 \( x \) の個数が \( 100 \) 個なので,
\( (n+1)^2-n^2+1=100 \)
\( 2n+2=100 \)
\( 2n=98 \)
\( n=49 \)
(6) 二つの箱A,Bがある。箱Aには \( 1 \) から \( 4 \) までの自然数が書いてある4枚のカード \( \fbox{1},\fbox{2},\fbox{3},\fbox{4} \) が入っており,箱Bには \( 4 \) から \( 8 \) までの自然数が書いてある5枚のカード \( \fbox{4},\fbox{5},\fbox{6},\fbox{7},\fbox{8} \) が入っている。A,Bそれぞれの箱から同時にカードを1枚ずつ取り出し,箱Aから取り出したカードに書いてある数を \( a \),箱Bから取り出したカードに書いてある数を \( b \) として,次の きまり にしたがって得点を決めるとき,得点が偶数である確率はいくらですか。A,Bそれぞれの箱において,どのカードが取り出されることも同様に確からしいものとして答えなさい。
きまり:\( a \) と \( b \) の最大公約数が \( 1 \) の場合は \( a+b \) の値を得点とし,
\( a \) と \( b \) の最大公約数が \( 1 \) 以外の場合は \( \sqrt{2ab} \) の値を得点とする。
【解説】
\( a \) と \( b \) の組み合わせとそれぞれの場合の得点を樹形図に書き出してみると,
得点が偶数になるのは7通り,すべての組み合わせは20通りなので,
求める確率は \( \dfrac{7}{20} \)

(7) \( a \) を一の位の数が \( 0 \) でない2けたの自然数とし,\( b \) を \( a \) の十の位の数と一の位の数とを入れかえてできる自然数とするとき,\( \dfrac{b^2-a^2}{99} \) の値が \( 24 \) である \( a \) の値をすべて求めなさい。
【解説】
\( a \) の十の位の数を \( x \),一の位の数を \( y \) とすると,
\( a=10x+y,b=10y+x \) と表すことができます。
ここから,
\( \dfrac{b^2-a^2}{99}=\dfrac{(b+a)(b-a)}{99} \)
\( =\dfrac{\{(10y+x)+(10x+y)\}\{(10y+x)-(10x+y)\}}{99} \)
\( =\dfrac{(11y+11x)(9y-9x)}{99} \)
\( =\dfrac{11(y+x) \times 9(y-x)}{99} \)
\( =(y+x)(y-x) \)
よって,\( (y+x)(y-x)=24 \) を満たす \( x,y \) の組み合わせを探せばいいことになります。
\( (y+x)(y-x)=24 \) より,\( y+x \) と \( y-x \) は,ともに \( 24 \) の約数です。
また,\( x,y \) は,ともに正の整数なので,\( y+x \) も正の整数です。
さらに,\( y+x \) と \( 24 \) は,ともに正の数なので,
「正の数 \( \times \) 正の数 \( = \) 正の数 」より,\( y-x \) も正の整数であり,
\( y>x \) であることもわかります。
ここから,あてはまる \( (y+x,y-x) \) の考えられる組み合わせは,
\( (y+x,y-x)=(12,2),(8,3),(6,4) \)
の3つであり,それぞれの組み合わせについて,あてはまる \( x,y \) の組み合わせを考えます。
(参考)
\( y+x \) は,正の整数 \( y \) に正の整数 \( x \) を足したもの,
\( y-x \) は,正の整数 \( y \) から正の整数 \( x \) をひいたもの,
なので,必ず \( y+x>y-x \) となります。
数直線で表すと ・・・

【\( (y+x,y-x)=(12,2) \) の場合】
連立方程式 \( \left\{ \begin{array}{}
y+x=12 \\
y-x=2 \\
\end{array} \right. \) を解くと, \( x=5,y=7 \)
【\( (y+x,y-x)=(8,3) \) の場合】
連立方程式 \( \left\{ \begin{array}{}
y+x=8 \\
y-x=3 \\
\end{array} \right. \) を解くと, \( x=\dfrac{5}{2},y=\dfrac{11}{2} \)
\( x,y \) が,整数ではないのであてはまらない。
【\( (y+x,y-x)=(6,4) \) の場合】
連立方程式 \( \left\{ \begin{array}{}
y+x=6 \\
y-x=4 \\
\end{array} \right. \) を解くと, \( x=1,y=5 \)
以上より,あてはまる \( a \) の値は,\( a=15,57 \)
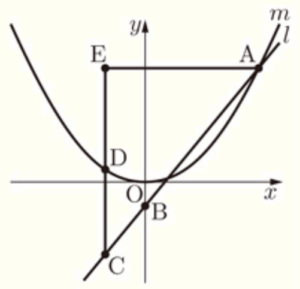
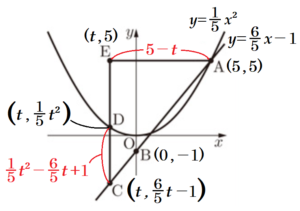
(8) 右図において,\( m \) は関数 \( y=\dfrac{1}{5}x^2 \) のグラフを表す。\( A \) は \( m \) 上の点であり,その \( x \) 座標は \( 5 \) である。\( B \) は \( y \) 軸上の点であり,その \( y \) 座標は \( -1 \) である。\( l \) は,2点 \( A,B \) を通る直線である。\( C \) は \( l \) 上の点であり,その \( x \) 座標は負である。\( C \) の \( x \) 座標を \( t \) とし,\( t<0 \) とする。\( D \) は,\( C \) を通り \( y \) 軸に平行な直線と \( m \) との交点である。\( E \) は,\( A \) を通り \( x \) 軸に平行な直線と直線 \( DC \) との交点である。 線分 \( DC \) の長さが線分 \( EA \) の長さより \( 3 \; cm \) 短いときの \( t \) の値を求めなさい。
答えを求める過程がわかるように,途中の式を含めた求め方も説明すること。ただし,原点 \( O \) から点 \( (1,0) \) までの距離,原点 \( O \) から点 \( (0,1) \) までの距離はそれぞれ \( 1 \; cm \) であるとする。
【解答】
\( A \) は \( y=\dfrac{1}{5}x^2 \) 上の点で,
\( x \) 座標は \( 5 \) なので,
\( y=\dfrac{1}{5} \times 5^2=5 \) となり,
\( A \) の座標は,\( A(5,5) \)
\( E \) の \( y \) 座標は,\( A \) の \( y \) 座標と等しいので,
\( E \) の座標は,\( E(t,5) \)
ここから,線分 \( EA \) の長さは,\( 5-t \; (cm) \)
\( B \) の座標は,\( B(0,-1) \) であり,
直線 \( l \) は \( A(5,5),B(0,-1) \) を通るので,
直線 \( l \) の式は \( y=\dfrac{6}{5}x-1 \)
ここから,\( C \) の座標は,\( C \left( t,\dfrac{6}{5}t-1 \right) \)
\( D \) は \( y=\dfrac{1}{5}x^2 \) 上の点で,
\( x \) 座標は \( t \) なので,\( y=\dfrac{1}{5}t^2 \) となり,
\( D \) の座標は,\( D \left( t,\dfrac{1}{5}t^2 \right) \)
ここから,線分 \( DC \) の長さは,
\( \dfrac{1}{5}t^2- \left( \dfrac{6}{5}t-1 \right)=\dfrac{1}{5}t^2-\dfrac{6}{5}t+1 \; (cm) \)
よって,線分 \( DC \) と線分 \( EA \) の長さの関係を方程式にして解くと,
\( \dfrac{1}{5}t^2-\dfrac{6}{5}t+1=5-t-3 \)
\( t^2-6t+5=-5t+10 \)
\( t^2-t-5=0 \)
\( t=\dfrac{1-\sqrt{21}}{2} \) (\( t<0 \) より)
大問2
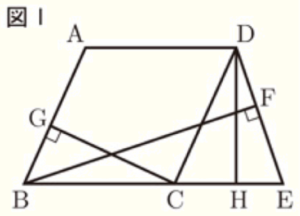
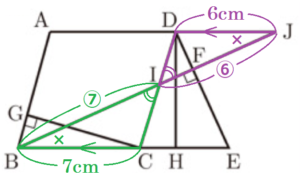
図Ⅰ,図Ⅱにおいて,四角形 \( ABCD \) は内角 \( ∠ABC \) が鋭角のひし形であり,\( AB=7 \; cm \) である。 \( △DCE \) は鋭角三角形であり,\( E \) は直線 \( BC \) 上にある。\( F \) は辺 \( DE \) 上にあって \( D,E \) と異なる点であり,\( B \) と \( F \) とを結んでできる線分 \( BF \) は辺 \( DE \) に垂直である。\( G \) は,\( C \) から辺 \( AB \) にひいた垂線と辺 \( AB \) との交点である。\( H \) は辺 \( CE \) 上の点であり,\( CH=GB \) である。\( D \) と \( H \) とを結ぶ。
次の問いに答えなさい。
(1) 図Ⅰにおいて,
① 四角形 \( ABCD \) の対角線 \( AC \) の長さを \( a \; cm \),四角形 \( ABCD \) の面積を \( S \; cm^2 \) とするとき, 四角形 \( ABCD \) の対角線 \( BD \) の長さを \( a,S \) を用いて表しなさい。
【解説】
対角線 \( BD \) の長さを \( b \; cm \) とすると,
ひし形の面積を求める公式より,
\( S=a \times b \times \dfrac{1}{2} \)
\( b=\dfrac{2S}{a} \)
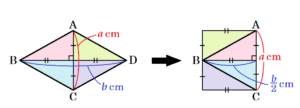
(参考)
ひし形の2本の対角線はそれぞれの中点で交わるので,
2本の対角線で4つに分かれた三角形を下の図のように並べ替えると,
縦 \( a \; cm \),横 \( \dfrac{b}{2} \; cm \) の長方形になるので,
\( S=a \times \dfrac{b}{2}=\dfrac{ab}{2} \)
\( b=\dfrac{2S}{a} \)
となります。
② \( △DHE \) ∽ \( △BFE \) であることを証明しなさい。
【解答】
\( △DHE \) と \( △BFE \) において,
\( ∠E \) は共通 ・・・ ➀
\( △DCH \) と \( △CBG \) において,
仮定より \( CH=BG \) ・・・ ➁
ひし形のすべての辺は等しいので,\( DC=CB \) ・・・ ③
\( CH=BG \) であり,錯角は等しいので,\( ∠DCH=∠CBG \) ・・・ ➃
➁➂➃より,2組の辺とその間の角がそれぞれ等しいので,
\( △DCH≡△CBG \)
対応する角は等しいので,\( ∠DHC=∠CGB=90° \) であり,\( DH⊥BE \)
\( DH⊥BE,BF⊥DE \) より,\( ∠DHE=∠BFE=90° \) ・・・ ➄
➀➄より,2組の角が等しいので,
\( △DHE \) ∽ \( △BFE \)
【解説】
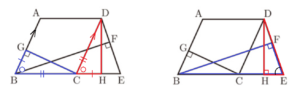
図1 \( △DCH≡△CBG \) 図2 \( △DHE \) ∽ \( △BFE \)
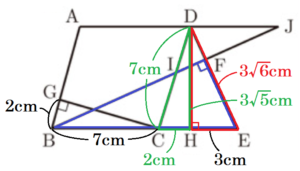
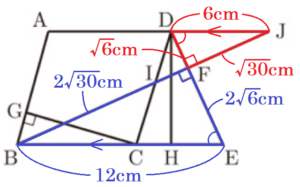
(2) 図Ⅱにおいて,\( GB=2 \; cm,HE=3 \; cm \) である。\( I \) は,線分 \( BF \) と辺 \( DC \) との交点である。\( J \) は,直線 \( BF \) と直線 \( AD \) との交点である。
① 線分 \( FE \) の長さを求めなさい。
【解答】
\( 2\sqrt{6} \; cm \)
【解説】
\( △DCH \) において,\( CH=GB=2 \; cm \),
\( CB=DC=7 \; cm \) なので,三平方の定理より,
\( DH^2=7^2-2^2=45 \)
\( DH=3\sqrt{5} \; (cm) \)
\( △DHE \) において,\( HE=3 \; cm \) なので,
三平方の定理より,
\( DE^2=(3\sqrt{5})^2+3^2=54 \)
\( DE=3\sqrt{6} \; (cm) \)
\( △DHE \) ∽ \( △BFE \) なので,
\( HE:FE=DE:BE \)
\( 3:FE=3\sqrt{6}:(7+2+3) \)
\( 3\sqrt{6}FE=36 \)
\( FE=2\sqrt{6} \; (cm) \)
② 線分 \( IJ \) の長さを求めなさい。
【解答】
\( \dfrac{18\sqrt{30}}{13} \; cm \)
【解説】
\( △JFD \) ∽ \( △BFE \) なので,
\( DE=3\sqrt{6} \; cm,FE=2\sqrt{6} \; cm \) より,
\( FD=3\sqrt{6}-2\sqrt{6}=\sqrt{6} \; (cm) \)
対応する辺の比は等しいので,
\( JD:BE=FD:FE \)
\( JD:12=\sqrt{6}:2\sqrt{6} \)
\( JD=6 \; (cm) \)
\( △JFD \) において,三平方の定理より,
\( JF^2=6^2-\sqrt{6}^2=30 \)
\( JF=\sqrt{30} \; (cm) \)
\( JF:BF=1:2 \) より,\( BF=2\sqrt{30} \; (cm) \)
\( △IDJ \) ∽ \( △ICB \) なので,
\( DJ=6 \; cm,CB=7 \; cm \) より,
\( IJ:IB=DJ:CB=6:7 \)
\( BJ=BF+JF=3\sqrt{30} \; (cm) \) なので,
\( IJ=\dfrac{6}{13}BJ=\dfrac{18\sqrt{30}}{13} \; (cm) \)
大問3
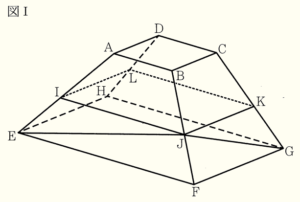
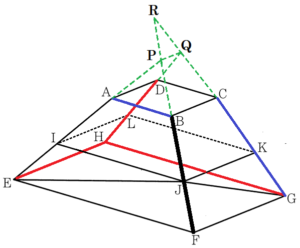
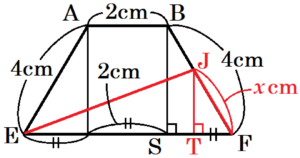
図Ⅰ,図Ⅱにおいて,立体 \( ABCD-EFGH \) は六つの平面で囲まれてできた立体である。四角形 \( ABCD \) は,1辺の長さが \( 2 \; cm \) の正方形である。四角形 \( EFGH \) は,\( EF=6 \; cm,FG=4 \; cm \) の長方形である。平面 \( ABCD \) と平面 \( EFGH \) は平行である。四角形 \( AEFB \) は \( AB//EF \) の台形であり,\( AE=BF=4 \; cm \) である。四角形 \( DHGC≡ \) 四角形 \( AEFB \) である。四角形 \( BFGC \) は \( BC//FG \) の台形である。四角形 \( AEHD≡ \) 四角形 \( BFGC \) である。
次の問いに答えなさい。
(1) 図Ⅰにおいて,四角形 \( IJKL \) は長方形であり,\( I,J,K,L \) はそれぞれ辺 \( AE,BF,CG,DH \) 上にある。このとき,\( AI=BJ=CK=DL \) である。\( E \) と \( J \),\( G \) と \( J \) とをそれぞれ結ぶ。
① 次のア~オのうち,辺 \( BF \) とねじれの位置にある辺はどれですか。すべて選び,記号を ○ で囲みなさい。
ア 辺 \( AB \) イ 辺 \( EH \) ウ 辺 \( CG \) エ 辺 \( GH \) オ 辺 \( DH \)
【解説】
ねじれの位置にある直線はどこまでいっても交わらない2直線のうち,平行でないものをいいます。
辺 \( AE,BF,CG,DH \) をそれぞれ上に延長し,
辺 \( AE \) と辺 \( BF \) の交点を点 \( P \),
辺 \( CG \) と辺 \( DH \) の交点を点 \( Q \) とすると,
立体 \( PQ-EFGH \) ができます。
よって,あてはまるものは
イ 辺 \( EH \),エ 辺 \( GH \),オ 辺 \( DH \)
になります。
ア 辺 \( AB \) は,点 \( B \) で辺 \( BF \) と交わっているのであてはまりません。
エ 辺 \( GH \) は,辺 \( BF,CG \) を点 \( P,Q \) より上側にさらに延長すると,点 \( R \) で辺 \( BF \) と交わるのであてはまりません。
なぜ四角すいにならないの?
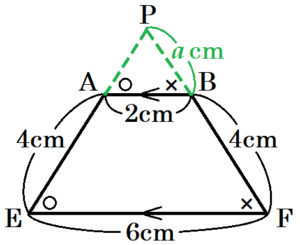
面 \( AEFB \) において,
\( △PAB \) ∽ \( △PEF \) なので,
\( PB=a \; cm \) とすると,
\( PB:PF=AB:EF \)
\( a:a+4=2:6 \)
\( 6a=2(a+4) \)
\( a=2 \; (cm) \)
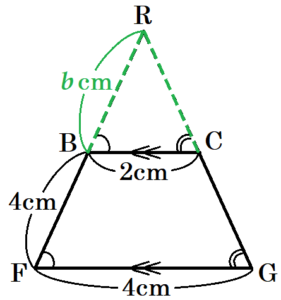
面 \( BFGC \) において,
\( △RBC \) ∽ \( △RFG \) なので,
\( RB=b \; cm \) とすると,
\( RB:RF=BC:FG \)
\( b:b+4=2:4 \)
\( 4b=2(b+4) \)
\( b=4 \; (cm) \)
点 \( P,R \) はどちらも辺 \( BF \) を延長した直線上の点なので,
上の図のような位置関係になるとわかります。
また,この関係は点 \( Q,R \) についても同じことがいえます。
➁ \( △JFG \) の面積は \( △JEF \) の面積の何倍ですか。
【解答】
\( \dfrac{\sqrt{5}}{3} \) 倍
【解説】
四角形 \( AEFB \) において,
点 \( B,J \) から辺 \( EF \) に垂線をひき,
交点を点 \( S,T \) とすると,
等脚台形であることから,
\( FS=\dfrac{EF-AB}{2}=\dfrac{6-2}{2}=2 \; (cm) \)
\( △BSF \) ∽ \( △JTF \) なので,\( JF=x \; cm \) とすると,
\( BF:JF=FS:FT \)
\( 4:x=2:FT \)
\( FT=\dfrac{1}{2}x \; (cm) \)
三平方の定理より,
\( JT^2=x^2-\left( \dfrac{1}{2}x \right)^2=\dfrac{3}{4}x^2 \)
\( JT=\dfrac{\sqrt{3}}{2}x \; (cm) \) ( \( JT>0 \) より)
このとき,
\( △JEF=EF \times JN \times \dfrac{1}{2} \)
\( =6 \times \dfrac{\sqrt{3}}{2}x \times \dfrac{1}{2} \)
\( =\dfrac{3\sqrt{3}}{2}x \; (cm^2) \)
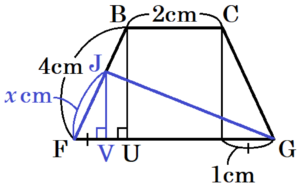
四角形 \( BFGC \) において,
点 \( B,J \) から辺 \( FG \) に垂線をひき,
交点を点 \( U,V \) とすると,
等脚台形であることから,
\( FU=\dfrac{FG-BC}{2}=\dfrac{4-2}{2}=1 \; (cm) \)
\( △BUF \) ∽ \( △JVF \) なので,
\( BF:JF=FU:FV \)
\( 4:x=1:FV \)
\( FV=\dfrac{1}{4}x \; (cm) \)
三平方の定理より,
\( JV^2=x^2-\left( \dfrac{1}{4}x \right)^2=\dfrac{15}{16}x^2 \)
\( JV=\dfrac{\sqrt{15}}{4}x \; (cm) \) ( \( JV>0 \) より)
このとき,
\( △JFG=FG \times JT \times \dfrac{1}{2} \)
\( =4 \times \dfrac{\sqrt{15}}{4}x \times \dfrac{1}{2} \)
\( =\dfrac{\sqrt{15}}{2}x \; (cm^2) \)
以上より,
\( △JFG:△JEF=\dfrac{\sqrt{15}}{2}x:\dfrac{3\sqrt{3}}{2}x \)
\( △JFG:△JEF=\sqrt{5}:3 \)
\( 3△JFG=\sqrt{5}△JEF \)
\( △JFG=\dfrac{\sqrt{5}}{3}△JEF \)
よって,\( △JFG \) の面積は \( △JEF \) の面積の \( \dfrac{\sqrt{5}}{3} \) 倍
③ 四角形 \( IJKL \) の周の長さが \( 15 \; cm \) であるときの辺 \( JK \) の長さを求めなさい。
【解答】
\( \dfrac{19}{6} \; cm \)
【解説】
四角形 \( IJKL \) は長方形なので,\( IJ=KL,JK=LI \) であり,
周の長さが \( 15 \; cm \) であることから,
\( IJ+JK+KL+LI=15 \)
\( 2(IJ+JK)=15 \)
\( IJ+JK=\dfrac{15}{2} \; (cm) \)
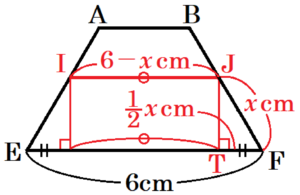
四角形 \( AEFB \) において,\( JF=x \; cm \) とすると,
問➁より,\( FT=\dfrac{1}{2}x \; cm \) と表せるので,
\( IJ=EF-2FT=6-x \; (cm) \)
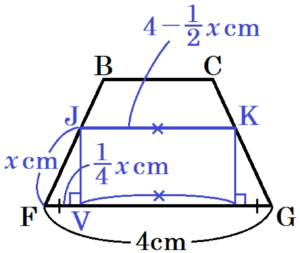
四角形 \( BFGC \) において,\( JF=x \; cm \) とすると,
問➁より,\( FV=\dfrac{1}{4}x \; cm \) と表せるので,
\( JK=FG-2FV=4-\dfrac{1}{2}x \; (cm) \)
\( IJ+JK=\dfrac{15}{2} \; (cm) \) なので,
\( (6-x)+\left( 4-\dfrac{1}{2}x \right)=\dfrac{15}{2} \)
\( (12-2x)+(8-x)=15 \)
\( -3x=-5 \)
\( x=\dfrac{5}{3} \)
このとき,
\( JK=4-\dfrac{1}{2} \times \dfrac{5}{3}=\dfrac{19}{6} \; (cm) \)
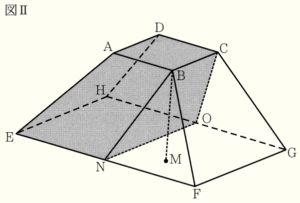
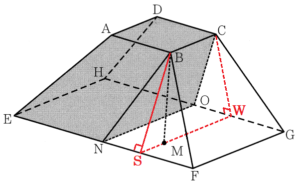
(2) 図Ⅱにおいて,\( M \) は \( B \) から平面 \( EFGH \) にひいた垂線と平面 \( EFGH \) との交点である。\( N,O \) は, それぞれ辺 \( EF,HG \) の中点である。このとき,4点 \( B,N,O,C \) は同じ平面上にあり,この4点を結んでできる四角形 \( BNOC \) は \( BC//NO \) の台形である。
① 線分 \( BM \) の長さを求めなさい。
【解答】
\( \sqrt{11} \; cm \)
【解説】
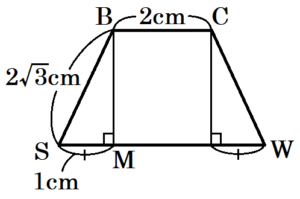
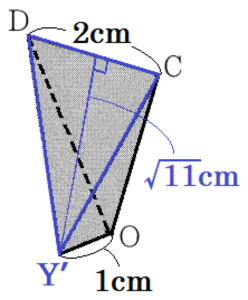
点 \( C \) から辺 \( GH \) に垂線をひき,
交点を点 \( W \) とすると,
点 \( M \) は,線分 \( SW \) 上の点になるので,
3点 \( B,C,M \) を通る面は,台形 \( BSWC \) になります。
\( SW//FG \) となることから,
\( SW=FG=4 \; cm \) なので,
\( SM=\dfrac{SW-BC}{2}=\dfrac{4-2}{2}=1 \; (cm) \)
四角形 \( AEFB \) において,
問(1)より,\( BF=4 \; cm,FS=2 \; cm \) なので,
\( BS=2\sqrt{3} \; cm \)
ここで,\( △BSM \) において,三平方の定理より,
\( BM^2=(2\sqrt{3})^2-1^2=11 \)
\( BM=\sqrt{11} \; (cm) \) ( \( BM>0 \) より)
② 立体 \( ABCD-ENOH \) の体積を求めなさい。
【解答】
\( \dfrac{23\sqrt{11}}{3} \; cm^3 \)
【解説】
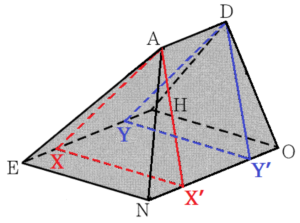
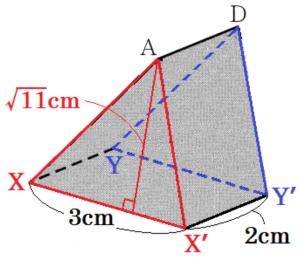
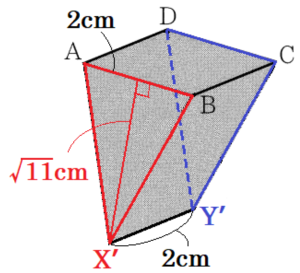
立体 \( ABCD-ENOH \) を面 \( ANOD \) で切ると,
立体 \( AD-ENOH \) と立体 \( NO-ABCD \) に分かれます。

さらに,立体 \( AD-ENOH \) を
点 \( A \) を通り,面 \( ENOH \) と垂直な面 \( AXX’ \) と
点 \( D \) を通り,面 \( ENOH \) と垂直な面 \( DYY’ \)
で切断すると,
四角すい \( A-ENX’X \),
三角柱 \( AXX’-DYY’ \),
四角すい \( D-YY’OH \)
の3つに分かれます。
( \( XX’//EN,YY’//OH \) とします)
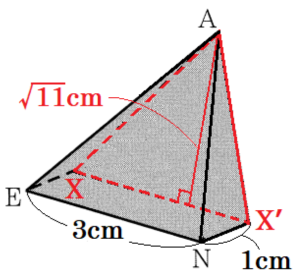
【四角すい \( A-ENX’X \) の体積】
点 \( N \) は辺 \( EF \) の中点なので,\( EN=3 \; cm \)
面 \( AXX’⊥ \) 面 \( ENOH \),\( XX’//EN \) より,
線分 \( XX’ \) を延長すると,点 \( M \) を通るので,
\( NX’=SM=1cm \)
点 \( A \) から面 \( ENX’X \) にひいた垂線が高さになるので,
\( BM \) と等しく,\( \sqrt{11} \; cm \)
ここから,体積は,
\( 3 \times 1 \times \sqrt{11} \times \dfrac{1}{3}=\sqrt{11} \; (cm^3) \)
【三角柱 \( AXX’-DYY’ \) の体積】
\( △AXX’ \) を底面と考えると,高さ \( X’Y’=2 \; cm \) になるので,
体積は,
\( \left( 3 \times \sqrt{11} \times \dfrac{1}{2} \right) \times 2 =3\sqrt{11} \; (cm^3) \)
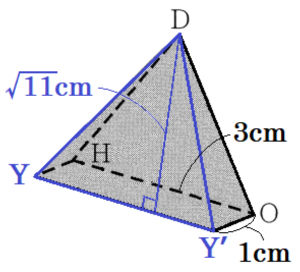
【四角すい \( D-YY’OH \) の体積】
四角すい \( A-ENX’X \) と同じ考え方で,
体積は,
\( 3 \times 1 \times \sqrt{11} \times \dfrac{1}{3}=\sqrt{11} \; (cm^3) \)
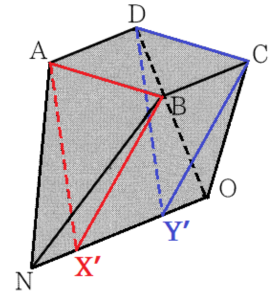
次に,立体 \( NO-ABCD \) を
辺 \( AB \) を通り,面 \( ABCD \) と垂直な面 \( ABX’ \) と
点 \( CD \) を通り,面 \( ABCD \) と垂直な面 \( CDY’ \) で切断すると,
三角すい \( N-ABX’ \),
三角柱 \( ABX’-DCY’ \),
三角すい \( O-CDY’ \)
の3つに分かれます。
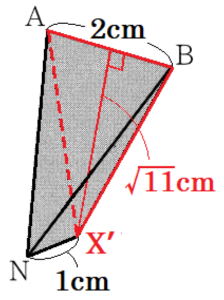
【三角すい \( N-ABX’ \) の体積】
\( △ABW’ \) を底面と考えると,
点 \( X’ \) から辺 \( AB \) にひいた垂線は \( BM \) と等しいので,\( \sqrt{11} \; cm \),
\( AB=2 \; cm,NX’=1cm \) より,体積は,
\( \left( 2 \times \sqrt{11} \times \dfrac{1}{2} \right) \times 1 \times \dfrac{1}{3} =\dfrac{\sqrt{11}}{3} \; (cm^3) \)
【三角柱 \( ABX’-DCY’ \) の体積】
\( △ABX’ \) を底面と考えると,高さ \( X’Y’=2 \; cm \) になるので,
体積は,
\( \left( 2 \times \sqrt{11} \times \dfrac{1}{2} \right) \times 2 =2\sqrt{11} \; (cm^3) \)
【三角すい \( O-CDY’ \) の体積】
三角すい \( N-ABX’ \) と同じ考え方で,体積は,
\( \left( 2 \times \sqrt{11} \times \dfrac{1}{2} \right) \times 1 \times \dfrac{1}{3} =\dfrac{\sqrt{11}}{3} \; (cm^3) \)
以上より,立体 \( ABCD-ENOH \) の体積は,
\( \sqrt{11}+3\sqrt{11}+\sqrt{11}+\dfrac{\sqrt{11}}{3}+2\sqrt{11}+\dfrac{\sqrt{11}}{3}=\dfrac{23\sqrt{11}}{3} \; (cm^3) \)