大問１
(1) (ア)〜(エ) の計算をしなさい。
(ア) \( -4-7 \)
(イ) \( -2(x+3y)+(x-3y) \)
(ウ) \( 8xy^2 \div (-2x) \)
(エ) \( (\sqrt{5}+1)^2 \)
(2) \( x^2-9y^2 \) を因数分解しなさい。
(3) 二次方程式 \( 2x^2-x-2=0 \) を解きなさい。
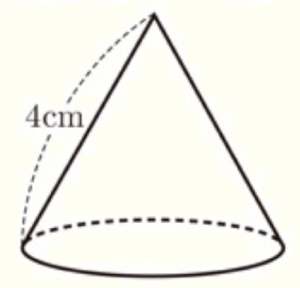
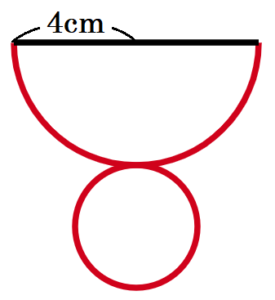
(4) 右の図のような母線の長さが \( 4 \; cm \) の円錐がある。この円錐の側面の展開図が半円になるとき，この円錐の底面の半径を求めなさい。
この円錐を展開すると，右の図のようになります。
おうぎ形（半円）の弧は底面の円周とぴったり重なっていたので，
長さは等しくなっています。
おうぎ形（半円）の弧の長さは，\( 2\pi{} \times 4 \times \dfrac{1}{2}=4\pi{} \; (cm) \) なので，
底面の半径を \( r \; cm \) とすると，
\( 2\pi{} \times r=4\pi{} \)
\( r=2 \; (cm) \)
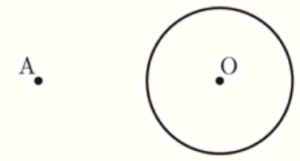
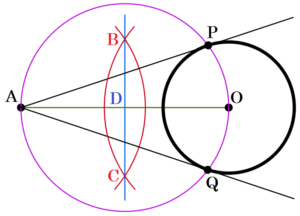
(5) 右の図のような点 \( A \) と点 \( O \) を中心とする円 \( O \) がある。点 \( A \) から円 \( O \) にひいた２本の接線を作図しなさい。
ただし，作図には定規とコンパスを用い、作図に用いた線は消さずに残しておくこと。
手順１ 点 \( A \) と点 \( O \) を中心に弧を描く。
（交点を点 \( B，C \) とします）
手順２ 点 \( B，C \) を通る直線を描く。
（線分 \( AO \) との交点を点 \( D \) とします）
手順３ 線分 \( AD \) を半径とする円を描く。
（円 \( O \) との交点を点 \( P，Q \) とします）
直線 \( AP，AQ \) が作図する接線になります。
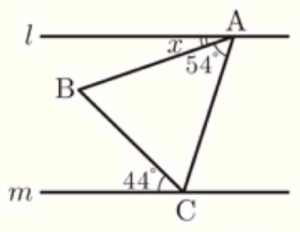
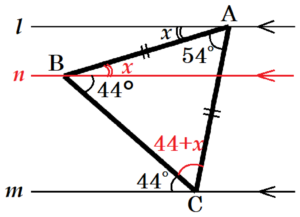
(6) 右の図のように，\( AB=AC \) である二等辺三角形 \( ABC \) がある。また，頂点 \( A \) を通る直線 \( l \) と，頂点 \( C \) を通る直線 \( m \) があり，\( l \) と \( m \) は平行である。このとき，\( ∠x \) の大きさを求めなさい。
頂点 \( B \) を通り，\( l，m \) と平行な直線 \( n \) を引くと，
錯角は等しいので，\( ∠ABC=44+x \) と表すことができます。
また，\( AB=AC \) より，\( ∠ACB=∠ABC=44+x \) なので，
\( △ABC \) において，
\( 54+(44+x)+(44+x)=180 \)
\( 2x+142=180 \)
\( x=19 \)
(7) 次の図は，ある都市における ２００３年，２０１２年，２０２１年の各月の最高気温をそれぞれ年別に箱ひげ図に表したものである。この箱ひげ図から読み取れることとして正しいものを，あとの➀～➄の中からすべて選び，番号を書きなさい。
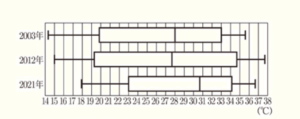
➀ 第３四分位数は，２０２１年が最も大きい。
➁ 四分位範囲は，２０１２年が最も大きい。
➂ ２０２１年では，最高気温が２０℃以下の月は１つしかない。
➃ ２０１２年では，２５%以上の月が，最高気温が３４℃以上である。
➄ ２００３年では，最高気温の平均値は２８℃である。
大問２
(1) ユウさんとルイさんが，学校の【宿題】についてあとのような【会話】をしている。
【会話】を踏まえて，(ア)〜(ウ)の各問いに答えなさい。
【宿題】
連立方程式を利用して解く問題をつくりなさい。また，その問題を解くために利用する連立方程式をつくりなさい。
【会話】
ユウ：学校の【宿題】について，このように考えたよ。
【ユウさんがつくった問題】
家から \( 1640 m \) 離れた学校へ行くために，はじめは歩いていましたが，遅刻しそうになったので，途中から分速 \( 100 m \) で走りました。すると，家を出発して２２分後に学校に着きました。
このとき，歩いた道のりと，走った道のりをそれぞれ求めなさい。
【ユウさんがつくった連立方程式】
\( \left\{
\begin{array}{}
x+y=1640 \\
\dfrac{x}{60}+\dfrac{y}{100}=22
\end{array} \right. \)
ルイ：【ユウさんがつくった連立方程式】では，何を \( x \) と \( y \) でそれぞれ表したの。
ユウ：歩いた ① を \( x \) ，走った ① を \( y \) と表したよ。
ルイ：そうなんだね。けれども，【ユウさんがつくった問題】から【ユウさんがつくった連立方程式】はつくれるのかな。【ユウさんがつくった問題】には何かが足りない気がするけど。
ユウ：本当だ。歩いた速さは分速 ➁ m であることを書き忘れていたよ。
ルイ：そうか。歩いた速さを書き加えればいいね。そういえば，\( x \) と \( y \) で表すものを変えて，同じ問題から別の連立方程式をつくる学習をしたね。【ユウさんがつくった問題】に歩いた速さは分速 ➁ \( m \) であることを書き加えて，別の連立方程式をつくれないかな。
ユウ：歩いた ③ を \( x \) ，走った ③ を \( y \) と表して連立方程式をつくれそうだ。このとき、連立方程式は，
\( \left\{
\begin{array}{}
\;\;\;\;\; ➃ \;\;\;\;\; =1640 \\
\;\;\;\;\; ➄ \;\;\;\;\; =22
\end{array} \right. \)
になるよ。
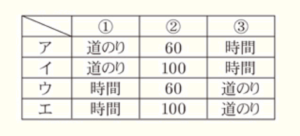
(ア) 【会話】の中の ① ～ ③ にあてはまる語句や数の組み合わせとして正しいものを，下のア〜エの中から１つ選び，記号を書きなさい。
ただし，道のりの単位は \( m \) とし，時間の単位は 分 とする。
(イ) 【会話】の中の ④ ， ⑤ にあてはまる式を \( x，y \) を用いて表しなさい。
(ウ) 【会話】を踏まえて，歩いた道のりを求めなさい。
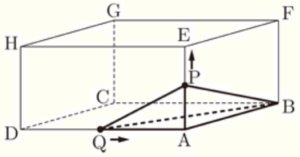
(2) 右の図のように，\( AB=9 cm，AD=12 cm， \)
\( AE=6 cm \) の直方体がある。点 \( P \) は，\( A \) を出発して辺 \( AE \) 上を毎秒 \( 1 \; cm \) の速さで \( E \) まで動く。点 \( Q \) は，\( D \) を出発して辺 \( DA \) 上を毎秒 \( 2 \; cm \) の速さで \( A \) まで動く。また，点 \( P \) と点 \( Q \) は同時に出発し，出発してからの時間を \( x \) 秒とする。ただし，\( 0≦x≦6 \) とする。
このとき，(ア)～(ウ)の各問いに答えなさい。
(ア) 点 \( P \) と点 \( Q \) が出発してから \( 3 \) 秒後の三角錐 \( PABQ \) の体積を求めなさい。
(イ) 点 \( Q \) が出発してから \( x \) 秒後の線分 \( QA \) の長さを \( x \) を用いて表しなさい。
(ウ) 三角錐 \( PABQ \) の体積が \( 24 \; cm^3 \) になるのは，点 \( P \) と点 \( Q \) が出発してから何秒後か求めなさい。
ただし，\( x \) についての方程式をつくり，答えを求めるまでの過程も書きなさい。
大問３
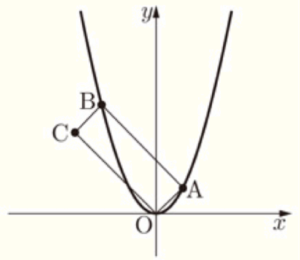
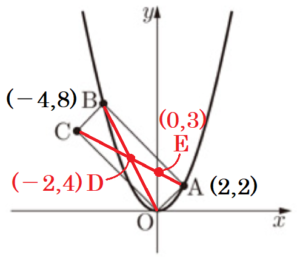
右の図のように，関数 \( y=ax^2 \) のグラフ上に２点 \( A(2，2) ，B(-4，8) \) がある。また，四角形 \( OABC \) が平行四辺形となるように点 \( C \) をとる。
このとき，次の (1)～(4) の各問いに答えなさい。
(1) \( a \) の値を求めなさい。
(2) 直線 \( AB \) の式を求めなさい。
(3) 点 \( C \) の座標を求めなさい。
(4) 四角形 \( OABC \) の対角線 \( OB \) と \( AC \) の交点を \( D \) とする。
このとき，(ア)～(ウ)の各問いに答えなさい。
(ア) \( OD：DB \) を求めなさい。
(イ) \( △OAD \) の面積を求めなさい。
（ア）より，\( OD：DB=1：1 \) なので，
\( D \) の \( x \) 座標は，\( \dfrac{-4+0}{2}=-2 \)
\( D \) の \( y \) 座標は，\( \dfrac{8+0}{2}=4 \)
線分 \( AD \) と \( y \) 軸の交点を \( E \) とすると，
\( A，E，D \) の \( x \) 座標がそれぞれ \( 2，0，-2 \) なので，
\( E \) は，線分 \( AD \) の中点になっています。
よって， \( E \) の \( y \) 座標は，\( \dfrac{4+2}{2}=3 \)
線分 \( OE \) を底辺として考えると，
\( △OAD=△ODE+△OAE \)
\( =3 \times 2 \times \dfrac{1}{2}+3 \times 2 \times \dfrac{1}{2} \)
\( =6 \)
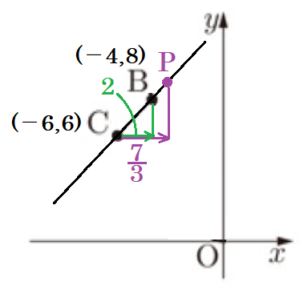
(ウ) 直線 \( BC \) 上に点 \( P \) をとる。\( △OAD \) と \( △OPC \) の面積比が \( 3：7 \) となるような点 \( P \) の \( x \) 座標をすべて求めなさい。
平行四辺形の対角線はそれぞれの中点で交わるので，
\( OD=BD \) であり，\( △OAD=△ABD \)
（イ）より，\( △OAD=6 \) なので，
\( △OAB=△OAD+△ABD=12 \)
平行四辺形を対角線で分けた２つの三角形の面積は等しいので，
\( △OBC=△OAB=12 \)
よって，\( △OAD：△OBC=1：2 \)
\( △OAD：△OPC=3：7 \) より，\( △OBC：△OPC=6：7 \) なので，
このときの \( △OPC \) の面積は，
\( △OBC：△OPC=6：7 \)
\( 12：△OPC=6：7 \)
\( △OPC=14 \)
になります。
条件より，直線 \( BC \) 上に点 \( P \) をとるので，
\( △OBC \) の底辺を \( BC \)，\( △OPC \) の底辺を \( CP \) とすると，
２つの三角形は高さが共通になっています。
ここから，\( △OBC：△OPC=6：7 \) のとき，
\( BC：PC=6：7 \) になります。
このとき，\( BC：PC=6：7 \) となるような点 \( P \) は，
点 \( B \) 側と点 \( C \) 側の２つあることに注意が必要です。
【点 \( P \) が，点 \( B \) 側にあるとき】
点 \( C \) から見て，点 \( B \) は \( x \) 軸方向に \( 2 \) 進んだ位置にあります。
\( BC：PC=6：7 \) になるとき，点 \( C \) から見て，点 \( P \) は \( x \) 軸方向に \( 2 \times \dfrac{7}{6}=\dfrac{7}{3} \) 進んだ位置にあります。
よって，点 \( P \) の \( x \) 座標は，\( -6+\dfrac{7}{3}=-\dfrac{11}{3} \)
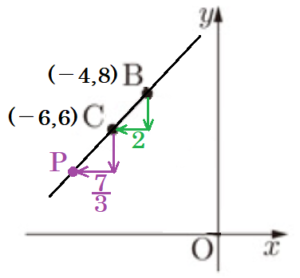
【点 \( P \) が，点 \( C \) 側にあるとき】
点 \( B \) から見て，点 \( C \) は \( x \) 軸方向に \( -2 \) 進んだ位置にあります。
\( BC：PC=6：7 \) になるとき，点 \( C \) から見て，点 \( P \) は \( x \) 軸方向に \( -2 \times \dfrac{7}{6}=-\dfrac{7}{3} \) 進んだ位置にあります。
よって，点 \( P \) の \( x \) 座標は，\( -6+\left( -\dfrac{7}{3} \right)=-\dfrac{25}{3} \)
大問４
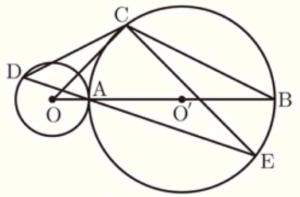
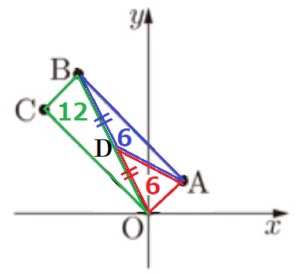
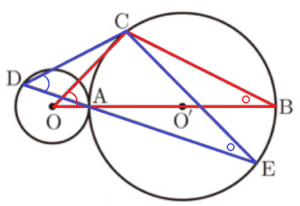
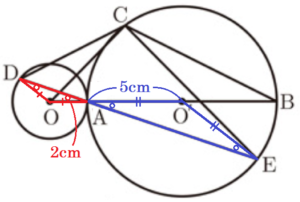
右の図のように，点 \( O \) を中心とする円 \( O \) と点 \( O‘ \) を中心とする円 \( O‘ \) があり，２つの円は線分 \( OO‘ \) 上の点 \( A \) を通る。また，\( OA=2 cm，O’A=5 cm \) となっている。直線 \( OO‘ \) と円 \( O‘ \) との交点のうち点 \( A \) と異なる点を \( B \) とし，円 \( O‘ \) の周上に \( BC=4\sqrt{5} \; cm \) となる点 \( C \) をとる。さらに、円 \( O \) の周上に \( ∠COA=∠CDA \) となる点 \( D \) をとる。また，直線 \( DA \) と円 \( O‘ \) との交点のうち点 \( A \) と異なる点を \( E \) とすると \( AE=3\sqrt{10} \; cm \) である。
このとき，次の (1)～(3) の各問いに答えなさい。
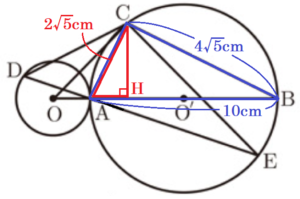
(1) 線分 \( AC \) の長さを求めなさい。
(2) \( △OBC \) ∽ \( △DEC \) であることを証明しなさい。
\( △OBC \) と \( △DEC \) において，
円 \( O‘ \) における弧 \( AC \) の円周角なので，
\( ∠CBO=∠CED \) ･･･ ➀
仮定より，
\( ∠COB=∠CDE \) ･･･ ➁
➀➁より，２組の角がそれぞれ等しいので，
\( △OBC \) ∽ \( △DEC \)
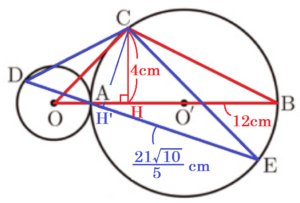
(3) 点 \( C \) から線分 \( AB \) に垂線をひき，その垂線と線分 \( AB \) との交点を \( H \) とする。
このとき，(ア)〜(ウ)の各問いに答えなさい。
(ア) 線分 \( CH \) の長さを求めなさい。
\( △ACH \) ∽ \( △ABC \) なので，
\( AC：AB=CH：BC \)
\( 2\sqrt{5}：10=CH：4\sqrt{5} \)
\( CH=4 \; (cm) \)
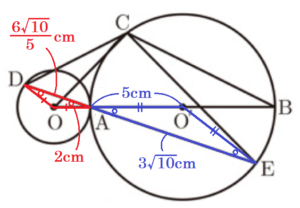
(イ) \( △OAD \) の面積を \( S \)，\( △O’AE \) の面積を \( T \) とするとき，\( S：T \) を最も簡単な整数の比で表しなさい。
\( △OAD \) ∽ \( △O’AE \) で，相似比は \( 2：5 \)
相似な三角形の面積比は相似比の２乗の比になるので，
\( S：T=2^2：5^2=4：25 \)
対頂角は等しいので，
\( ∠OAD=∠O’AE \) ･･･ ➀
\( △OAD \) は二等辺三角形なので，
\( ∠ODA=∠OAD \) ･･･ ➁
\( △O’AE \) は二等辺三角形なので，
\( ∠O’EA=∠O’AE \) ･･･ ➂
➀➁➂より，
\( ∠ODA=∠O’EA \) ･･･ ➃
➀➃より，２組の角がそれぞれ等しいので，
\( △OAD \) ∽ \( △O’AE \)
(ウ) \( △DEC \) の面積を求めなさい。
ここまでの問題で誘導されてきた内容を利用して求めます。
（イ）で確認した通り，\( △OAD \) ∽ \( △O’AE \) で，相似比は \( 2：5 \) なので，
\( AD：AE=2：5 \)
\( AD：3\sqrt{10}=2：5 \)
\( AD=\dfrac{6\sqrt{10}}{5} \; (cm) \)
\( DE=AD+AE \)
\( =\dfrac{6\sqrt{10}}{5}+3\sqrt{10} \)
\( =\dfrac{21\sqrt{10}}{5} \; (cm) \)
\( △CDE \) において，点 \( C \) から線分 \( DE \) に垂線をひき，交点を \( H’ \) とします。
(2) より \( △OBC \) ∽ \( △DEC \) なので，
\( OB：DE=CH：CH’ \)
\( 12：\dfrac{21\sqrt{10}}{5}=4：CH’ \)
\( CH’=\dfrac{7\sqrt{10}}{5} \; (cm) \)
以上より，
\( △DEC=DE \times CH’ \times \dfrac{1}{2} \)
\( =\dfrac{21\sqrt{10}}{5} \times \dfrac{7\sqrt{10}}{5} \times \dfrac{1}{2} \)
\( =\dfrac{147}{5} \; (cm^2) \)
大問５
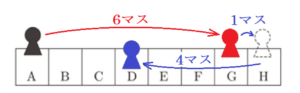
(1) １つのさいころを２回投げて【図】のようなマスの上でコマを動かす。コマはあとの【ルール】に従って動かすものとする。
このとき【例】を参考にして，(ア)〜(エ)の各問いに答えなさい。
ただし，さいころの目の出方はどの目も同様に確からしいとする。また，最初，コマは \( A \) のマスにあるものとする。
【ルール】
・ さいころを投げて，出た目の数だけコマを動かす。
・ \( A \) から \( H \) の方向にコマを動かし，\( H \) に到達したら折り返して \( H \) から \( A \) の方向にコマを動かす。
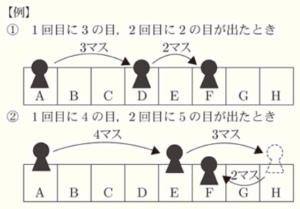
(ア) １回目に６の目，２回目に５の目が出たとき，コマは \( A～H \) のどのマスにあるか，記号を書きなさい。
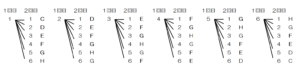
(イ) コマが \( A \) のマスにある確率を求めなさい。
求める確率は \( 0 \)
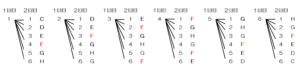
(ウ) コマが \( F \) のマスにある確率を求めなさい。
すべての場合の数は３６通り，\( F \) のマスに止まるのは８通りなので，
求める確率は \( \dfrac{8}{36}=\dfrac{2}{9} \)
(エ) コマが \( H \) のマスにない確率を求めなさい。
［\( H \) のマスにない確率］\( =1- \)［\( H \) のマスにある確率］ で求めることができます。
さいころの目の組み合わせとコマの行き先を樹形図で表すと，
すべての場合の数は３６通り，\( H \) のマスに止まるのは６通りなので，
\( H \) のマスにある確率は \( \dfrac{6}{36}=\dfrac{1}{6} \)
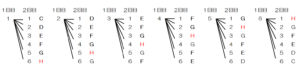
よって，［\( H \) のマスにない確率］\( =1-\dfrac{1}{6}=\dfrac{5}{6} \)
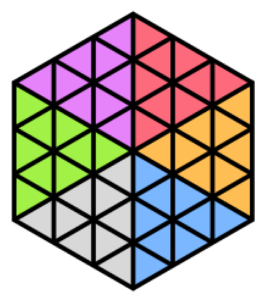
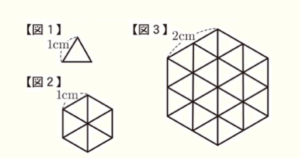
(2) 【図１】のような１辺の長さが \( 1 \; cm \) の正三角形のタイルをすき間なく並べて正六角形をつくる。
例えば，１辺の長さが \( 1 \; cm \) の正六角形をつくると【図２】のようになる。また，１辺の長さが \( 2 \; cm \) の正六角形をつくると【図３】のようになる。
このとき，(ア)〜(ウ)の各問いに答えなさい。
(ア) １辺の長さが \( 3 \; cm \) の正六角形を１個つくるとき，ちょうど何枚のタイルが必要か求めなさい。
できた正六角形を図のように６つの正三角形に分けると，
１つの正三角形は９枚でできているので，
全部で５４枚のタイルが必要。
(イ) １辺の長さが \( 6 \; cm \) の正六角形を１個つくるとき，ちょうど何枚のタイルが必要か求めなさい。
（ア）と同じ方法で何枚のタイルが必要か確認します。
１辺の長さが \( 1 \; cm \) の場合 ･･･ \( 6 \)枚 \( =1 \)枚 \( \times \; 6 \)色 \( =1^2 \)枚 \( \times \; 6 \)色
１辺の長さが \( 2 \; cm \) の場合 ･･･ \( 24 \)枚 \( =4 \)枚 \( \times \; 6 \)色 \( =2^2 \)枚 \( \times \; 6 \)色
１辺の長さが \( 3 \; cm \) の場合 ･･･ \( 54 \)枚 \( =9 \)枚 \( \times \; 6 \)色 \( =3^2 \)枚 \( \times \; 6 \)色
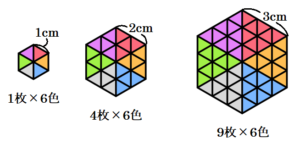
ここから，１辺の長さが \( 6 \; cm \) の場合は，\( 6^2 \)枚 \( \times \; 6 \)色 \( =216 \)枚
(ウ) 【図１】のタイルが２０２３枚あるとき，つくることができる正六角形の中で，最も大きな正六角形の１辺の長さを求めなさい。
ただし，正六角形の１辺の長さを表す数は整数とする。
