大問１
(1) 次の➀～④の計算をしなさい。
➀ \( 1-6 \)
➁ \( 2(x+3y)-(5x-4y) \)
➂ \( 15a^2b \div 3ab^3 \times b^2 \)
➃ \( \dfrac{9}{\sqrt{3}}-\sqrt{12} \)
(2) \( x^2-6x+9 \) を因数分解しなさい。
大問２
(1) 下の図は、ある中学校の３年生２５人が受けた国語、数学、英語のテストの得点のデータを箱ひげ図で表したものである。
このとき、これらの箱ひげ図から読み取れることとして正しく説明しているものを、次のア～エの中から２つ選んで、その記号を書きなさい。
ア ３教科の中で国語の平均点が一番高い。
イ ３教科の合計点が６０点以下の生徒はいない。
ウ １３人以上の生徒が６０点以上の教科はない。
エ 英語で８０点以上の生徒は６人以上いる。
(2) \( \dfrac{252}{n} \) の値が，ある自然数の２乗となるような，最も小さい自然数 \( n \) の値を求めなさい。
(3) \( x \) についての２次方程式 \( x^2+3ax+a^2-7=0 \) がある。
\( a=-1 \) のとき，この２次方程式を解きなさい。
(4) チョコレートが何個かと，それを入れるための箱が何個かある。１個の箱にチョコレートを３０個ずつ入れたところ，すべての箱にチョコレートを入れてもチョコレートは２２個余った。そこで，１個の箱にチョコレートを３５個ずつ入れていったところ，最後の箱はチョコレートが３２個になった。
このとき、箱の個数を求めなさい。
大問３
下の図１のように \( \fbox{1} \) から \( \fbox{7} \) までの番号の書かれた階段がある。地面の位置に太郎さん，\( \fbox{7} \) の段の位置に花子さんがいる。太郎さん，花子さんがそれぞれさいころを１回ずつ振り，自分が出した目の数だけ，太郎さんは \( \fbox{1} \; ，\fbox{2} \; ，\fbox{3} \)，･･･ と階段を上り，花子さんは \( \fbox{6} \; ，\fbox{5} \; ，\fbox{4} \) ，･･･ と階段を下りる。例えば，太郎さんが２の目を出し，花子さんが１の目を出したときは，下の図２のようになる。 また，２段離れているとは，例えば，図３のような状態のこととする。
このとき、次の(1)～(3)の問いに答えなさい。
ただし、さいころは各面に１から６までの目が１つずつかかれており，どの目が出ることも同様に確からしいとする。
(1) 太郎さんと花子さんが同じ段にいる確率を求めなさい。
(2) 太郎さんと花子さんが２段離れている確率を求めなさい。
(3) 太郎さんと花子さんが３段以上離れている確率を求めなさい。
大問４
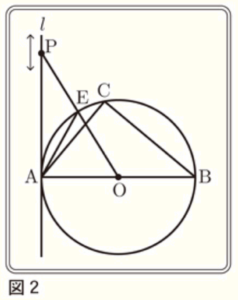
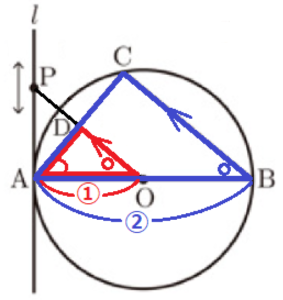
右の図１のように、タブレット端末の画面に長さが \( 14 \; cm \) の線分 \( AB \) を直径とする円 \( O \) が表示されている。さらに、円 \( O \) の円周上の２点 \( A，B \) と異なる点 \( C \)，点 \( A \) における円 \( O \) の接線 \( l \)，\( l \) 上の点 \( P \) が表示されている。 点 \( P \) は \( l \) 上を動かすことができ、太郎さんと花子さんは、点 \( P \) を動かしながら、図形の性質や関係について調べている。
このとき、次の(1)，(2)の問いに答えなさい。
(1) 太郎さんは線分 \( OP \) と線分 \( BC \) が平行になるように点 \( P \) を動かした。
➀ 線分 \( AC \) と線分 \( OP \) の交点を \( D \) とし，\( BC=10 \; cm \) とするとき、線分 \( OD \) の長さを求めなさい。
\( △AOD \) ∽ \( △ABC \)，\( AO：AB=1：2 \) なので，
\( OD：BC=AO：AB \)
\( OD：10=1：2 \)
\( OD=5 \; (cm) \)
➁ 太郎さんは，\( △ABC \) ∽ \( △POA \) であることに気づき、 次のように証明した。 ア ～ オ をうめて、証明を完成させなさい。
〈 証明 〉
\( △ABC \) と \( △POA \) において，
ア だから， イ \( =90° \) ･･･ ➀
直線 \( l \) は点 \( A \) における円 \( O \) の接線だから，\( ∠PAO=90° \) ･･･ ➁
➀，➁より， イ \( =∠PAO \) ･･･ ➂
平行線の同位角は等しいから， ウ \( = \) エ ･･･ ➃
➂，➃より， オ がそれぞれ等しいので、
\( △ABC \) ∽ \( △POA \)
ア ･･･ 直径 \( AB \) に対する円周角
イ ･･･ \( ∠ACB \)
ウ ･･･ \( ∠ABC \)
エ ･･･ \( ∠POA \)
オ ･･･ ２組の角
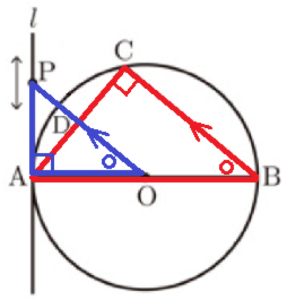
(2) 花子さんは，右の図２のように \( ∠AOP=60° \) となるように点 \( P \) を動かした。 線分 \( OP \) と円 \( O \) との交点を \( E \) とするとき，\( △APE \) の面積を求めなさい。
\( ∠AOP=60°，∠PAO=90° \) より，
\( △OAP \) は，\( 30°，60°，90° \) の直角三角形なので，
\( OP=2OA=14 \; (cm) \)
\( AP=\sqrt{3}OA=7\sqrt{3} \; (cm) \)
よって，
\( △OAP=AO \times AP \times \dfrac{1}{2} \)
\( =7 \times 7\sqrt{3} \times \dfrac{1}{2} \)
\( =\dfrac{49\sqrt{3}}{2} \; (cm^2) \)
また，円 \( O \) の半径なので，\( OA=OE=7 \; cm \) であり，
点 \( E \) は線分 \( OP \) の中点になっています。
\( △APE \) と \( △OAP \) において，線分 \( PE，OP \) を底辺と考えると，高さが共通になっています。
\( △APE \) と \( △OAP \) の面積比は底辺の長さの比と等しくなります。
よって，
\( △APE：△OAP=PE：OP \)
\( △APE：\dfrac{49\sqrt{3}}{2}=1：2 \)
\( △APE=\dfrac{49\sqrt{3}}{4} \; (cm^2) \)
大問５
\( O(0，0)，A(6，0)，B(6，6) \) とするとき，次の(1)，(2)の問いに答えなさい。
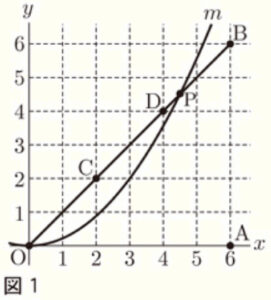
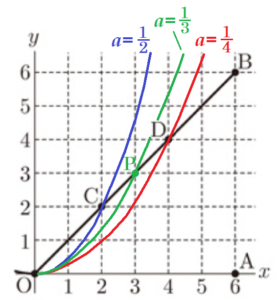
(1) 右の図１において，\( m \) は関数 \( y=ax^2 \; (a>0) \) のグラフを表し，\( C(2，2)，D(4，4) \) とする。
➀ \( m \) が点 \( B \) を通るとき，\( a \) の値を求めなさい。
➁ 次の文章の Ⅰ ～ Ⅲ に当てはまる語句の組み合わせを，下のア～カの中から１つ選んで，その記号を書きなさい。
点 \( P \) は Ⅱ の方に動く。 また，\( a \) の値を \( \dfrac{1}{3} \) とすると，点 \( P \) は Ⅲ 上にある。
ア Ⅰ 点 \( B \) Ⅱ 点 \( C \) Ⅲ 線分 \( OC \)
イ Ⅰ 点 \( B \) Ⅱ 点 \( C \) Ⅲ 線分 \( CD \)
ウ Ⅰ 点 \( B \) Ⅱ 点 \( C \) Ⅲ 線分 \( DB \)
エ Ⅰ 点 \( C \) Ⅱ 点 \( B \) Ⅲ 線分 \( OC \)
オ Ⅰ 点 \( C \) Ⅱ 点 \( B \) Ⅲ 線分 \( CD \)
カ Ⅰ 点 \( C \) Ⅱ 点 \( B \) Ⅲ 線分 \( DB \)
\( m \) が点 \( D \) を通る場合の \( a \) の値は
\( y=ax^2 \)
\( 4=a \times 4^2 \)
\( a=\dfrac{1}{4} \)
\( m \) が点 \( C \) を通る場合の \( a \) の値は
\( y=ax^2 \)
\( 2=a \times 2^2 \)
\( a=\dfrac{1}{2} \)
なので，
\( a \) の値を大きくしていくと，点 \( P \) は\( C \) の方に動き，
\( a \) の値を大きくしていくと，点 \( P \) は\( B \) の方に動きます。
また，\( a=\dfrac{1}{2} \) のときは点 \( C \) を通り，\( a=\dfrac{1}{4} \) のときは点 \( D \) を通るので，
\( \dfrac{1}{2}>\dfrac{1}{3}>\dfrac{1}{4} \) より，
\( a=\dfrac{1}{3} \) のときは線分 \( CD \) 上にあります。
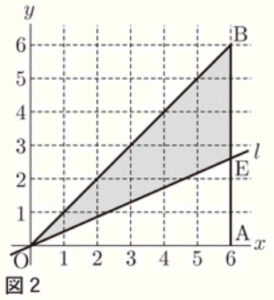
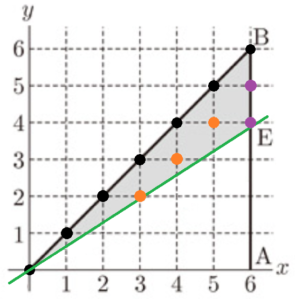
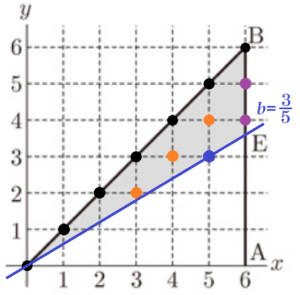
(2) 右の図２で，\( y=bx \) で表される直線 \( l \) と２点 \( A，B \) を除いた線分 \( AB \) が交わるとき，その交点を \( E \) とする。
このとき，次の [ 条件１ ] と [ 条件２ ] の両方を満たす点の個数が１２個になるのは，\( b \) がどのような値のときか。\( b \) のとりうる値の範囲を，不等号を使った式で表しなさい。
[ 条件２ ] \( △OEB \) の辺上または内部にある。
つまり，辺 \( BE，OE \) 上の点と \( △OEB \) 内部の点の合計が５個になるような
\( b \) の値の範囲を求めればいいことになります。
なお，原点 \( O \) は辺 \( OB \) 上の点，点\( E \) は辺 \( OE \) 上の点として数えることにします。
例えば，\( b=\dfrac{1}{2} \) の場合を考えると，
辺 \( BE \) 上の点 ● は２個，
辺 \( OE \) 上の点 ● は３個，
内部の点 ● は４個
で合計９個あります。
つまり，\( b \) は \( \dfrac{1}{2} \) より大きい値になることがわかります。
ちなみに，\( b=\dfrac{1}{2} \) の場合は，
感覚的に「もっと上にあるな」とわかる場合はやらなくても構いません。
次に，\( b=\dfrac{2}{3} \) の場合を考えると，
辺 \( BE \) 上の点 ● は１個，
辺 \( OE \) 上の点 ● は２個，
内部の点 ● は２個
で合計５個となり，
求める範囲に \( b=\dfrac{2}{3} \) が含まれるとわかります。
ここから，\( b \) の値が \( \dfrac{2}{3} \) より少しだけ大きくなった場合を考えると，
辺 \( BE \) 上の点 ● は１個，
内部の点 ● は２個
で合計３個となり，
求める範囲に \( b>\dfrac{2}{3} \) は含まれないとわかります。
\( b \) の値が \( \dfrac{2}{3} \) より少しだけ小さくなった場合を考えると，
辺 \( BE \) 上の点 ● は２個，
内部の点 ● は３個
で，合計５個となり，
引き続き求める範囲に含まれているとわかります。
そこから \( b=\dfrac{3}{5} \) まで小さくした場合を考えると，
辺 \( BE \) 上の点 ● は２個，
辺 \( OE \) 上の点 ● は１個，
内部の点 ● は３個
で合計６個となり，求める範囲に \( b=\dfrac{3}{5} \) は含まれないとわかります。
以上より，求める範囲は \( \dfrac{3}{5}<b≦\dfrac{2}{3} \) となります。
大問６
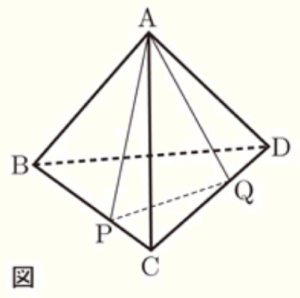
右の図のような，１辺が \( 6 \; cm \) の正四面体がある。辺 \( BC \) 上に \( BP：PC=2：1 \) となる点 \( P \)，辺 \( CD \) 上に \( CQ：QD=2：1 \) となる点 \( Q \) をとる。
このとき、次の(1)，(2)の問いに答えなさい。
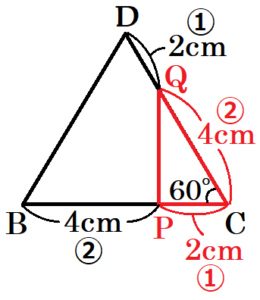
(1) \( △CPQ \) はどんな三角形か。最も適切なものを、次のア～エの中から１つ選んで，その記号を書きなさい。
ア 正三角形 イ 二等辺三角形 ウ 直角三角形 エ 直角二等辺三角形
正四面体の４つの面はすべて正三角形になので，
\( △BCD \) は正三角形であり，\( ∠BCD=60° \) ･･･ ➀
\( BC=CD=6 \; cm，BP：PC=CQ：QD=2：1 \) より，
\( PC=\dfrac{1}{3}BC=2 \; (cm) \)
\( CQ=\dfrac{2}{3}CD=4 \; (cm) \)
であり，\( PC：CQ=2：1 \) ･･･ ➁
➀➁より，
\( △CPQ \) は \( 30°，60°，90° \) の直角三角形になります。
(2) ➀ 線分 \( AQ \) の長さを求めなさい。
\( △ACD \) において，点 \( A \) から線分 \( CD \) に垂線をひき，
交点を点 \( R \) とすると，\( △ACD \) は正三角形なので，
\( RD=\dfrac{1}{2}CD=3 \; (cm) \)
\( △ARD \) は \( 30°，60°，90° \) の直角三角形なので，
\( AR=\sqrt{3}RD=3\sqrt{3} \; (cm) \)
また，\( RD=3 \; cm，QD=2 \; cm \) より，
\( RQ=RD-QD=1 \; (cm) \)
\( △ARQ \) において，三平方の定理より，
\( AQ^2=AR^2+RQ^2 \)
\( =(3\sqrt{3})^2+1^2 \)
\( =28 \)
\( AQ=2\sqrt{7} \; (cm) \)（\( AQ>0 \) より）
➁ 直線 \( AP \) を軸として，\( △APQ \) を１回転させてできる立体の体積を求めなさい。
ただし，円周率は \( \pi{} \) とする。
\( AC=AD=6 \; cm，CP=DQ=2 \; cm，∠ACP=∠ADQ \) より，
\( △ACP≡△ADQ \) なので，\( AP=AQ=2\sqrt{7} \; cm \)
(1) より，
\( △CPQ \) は \( CQ=4 \; cm，CP=2 \; cm，∠PCQ=60° \) の直角三角形なので，
\( PQ=\sqrt{3}CP=2\sqrt{3} \; (cm) \)
以上より，\( △APQ \) は，
３辺の長さが \( AP=AQ=2\sqrt{7} \; cm，PQ=2\sqrt{3} \; cm \) の二等辺三角形になります。
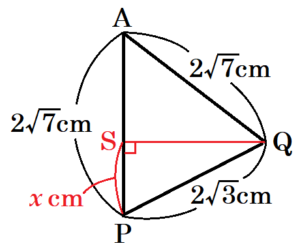
\( △APQ \) を辺 \( AP \) が垂直になるように描き，
点 \( Q \) から辺 \( AP \) に垂線をひいた交点を点 \( S \) とします。
線分 \( PS=x \; cm \) とすると，
\( △AQS \) と \( △PQS \) において，三平方の定理より
\( AQ^2-AS^2=PQ^2-PS^2 \)
\( (2\sqrt{7})^2-(2\sqrt{7}-x)^2=(2\sqrt{3})^2-x^2 \)
\( 4\sqrt{7}x-x^2=12-x^2 \)
\( 4\sqrt{7}x=12 \)
\( x=\dfrac{3}{\sqrt{7}} \; (cm) \)
このとき，先の計算過程より，\( AQ^2-AS^2=4\sqrt{7}x-x^2 \) なので，
\( QS^2=AQ^2-AS^2 \)
\( =4\sqrt{7} \times \dfrac{3}{\sqrt{7}}- \left( \dfrac{3}{\sqrt{7}} \right)^2 \)
\( =12-\dfrac{9}{7} \)
\( =\dfrac{75}{7} \)
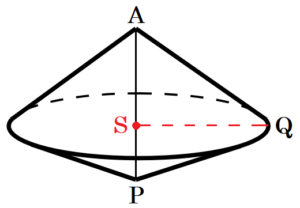
ここから，直線 \( AP \) を軸として，\( △APQ \) を１回転させてできる立体の体積を求めていきます。
回転させた立体は右の図のように円すいをくっつけた形になるので，
その立体の体積を \( V \) とすると，
\( V=\left( \pi{} \times QS^2 \times AS \times \dfrac{1}{3} \right)+\left( \pi{} \times QS^2 \times PS \times \dfrac{1}{3} \right) \)
\( =\dfrac{\pi{}}{3} \times QS^2 \times (AS+PS) \)
\( =\dfrac{\pi{}}{3} \times QS^2 \times AP \)
\( =\dfrac{\pi{}}{3} \times \dfrac{75}{7} \times 2\sqrt{7} \)
\( =\dfrac{50\sqrt{7}}{7}\pi{} \; (cm^3) \)
