大問1
(1)(ア)〜(エ)の計算をしなさい。
(ア) \( 3-(-5) \)
(イ) \( 2(x+3y)-5(2x+y) \)
【解説】
\( =2x+6y-10x-5y \)
\( =-8x+y \)
(ウ) \( 18x^2y \div (-12xy) \)
【解答】
\( -\dfrac{3x}{2} \) または \( -\dfrac{3}{2}x \)
【解説】
\( =-\dfrac{18x^2y}{12xy} \)
\( =-\dfrac{3x}{2} \)
(エ) \( (\sqrt{5}-\sqrt{2}) (\sqrt{5}+\sqrt{2}) \)
【解説】
\( =(\sqrt{5})^2-(\sqrt{2})^2 \)
\( =5-2 \)
\( =3 \)
(2) \( x^2y-6xy \) を因数分解しなさい。
(3) 二次方程式 \( x^2-x-1=0 \) を解きなさい。
【解答】
\( x=\dfrac{1±\sqrt{5}}{2} \)
【解説】
解の公式より
\( x=\dfrac{-(-1)±\sqrt{(-1)^2-4 \times 1 \times (-1)}}{2 \times 1} \)
\( =\dfrac{1±\sqrt{5}}{2} \)
(4) 下の図のような三角すいの体積を求めなさい。
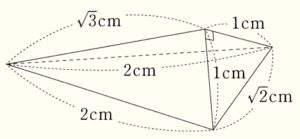
【解答】
\( \dfrac{\sqrt{3}}{6} \; cm^3 \)
【解説】
下左の図のように各頂点に \( A,B,C,D \) と名前をつけると,
面 \( ABD \) と辺 \( AC \) は垂直になっているので,
面 \( ABD \) を底面と考えると,辺 \( AC \) が高さになります。
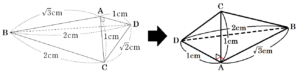
また,面 \( ABD \) は3辺の長さが \( 1:2:\sqrt{3} \) になっていることから,
\( ∠BAD=90° \) の直角三角形になっています。
よって,求める体積は,
\( \left(AD \times AB \times \dfrac{1}{2} \right) \times AC \times \dfrac{1}{3} \)
\( =\left(1 \times \sqrt{3} \times \dfrac{1}{2} \right) \times 1 \times \dfrac{1}{3} \)
\( =\dfrac{\sqrt{3}}{6} \; (cm^3) \)
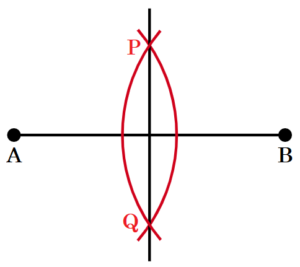
(5) 下の図のような線分 \( AB \) がある。線分 \( AB \) の垂直二等分線を作図しなさい。
ただし,作図には定規とコンパスを用い,作図に用いた線は消さずに残しておくこと。

【解答】
手順1 2点 \( A,B \) を中心に円弧を描く
(交点を \( P,Q \) とします)
手順2 2点 \( P,Q \) を通る直線を描く
手順2の直線が,線分 \( AB \) の垂直二等分線になります。
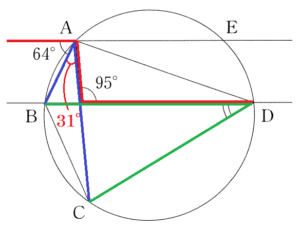
(6) 下の図のように,異なる5点 \( A,B,C,D,E \) が同じ円周上にあり,\( AE//BD \) である。このとき, \( ∠BDC \) の大きさを求めなさい。
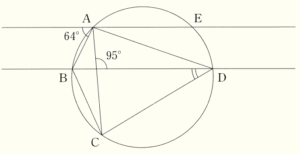
【解説】
\( AE//BD \) より,
\( ∠BAC+64°=95° \)
\( ∠BAC=31° \)
\( ∠BDC \) と \( ∠BAC \) は,
どちらも \( \stackrel{\huge\frown}{ BC } \) に対する円周角なので,
\( ∠BDC=∠BAC=31° \)
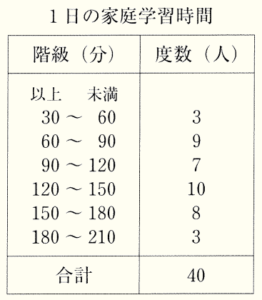
(7) 下の度数分布表は,あるクラスの生徒 \( 40 \) 人に対して,1日の家庭学習時間を調査した結果をまとめたものである。この度数分布表から読みとれることとして正しいものを,あとの ①~④ の中からすべて選び,番号を書きなさい。
① 最頻値は \( 135 \) 分である。
➁ 第1四分位数は,階級値が \( 105 \) 分の階級に
含まれる。
➂ \( 120 \) 分未満の累積度数は,\( 29 \) 人である。
➃ 範囲は \( 180 \) 分未満である。
【解説】
【正しい理由】
① ・・・ 最頻値は,度数が最も大きい階級の階級値のことをいいます。
度数が最も大きい階級は \( 120 \) 分以上 \( 150 \) 分未満の階級で,
その階級値は,\( \dfrac{120+150}{2}=135 \) 分になります。
➃ ・・・ 範囲は,「最大値 \( – \) 最小値」で求めることができます。
最小値となり得る最も小さい値は \( 30 \) 分,最大値となり得る最も大きい値は \( 209 \) 分なので,
範囲となり得る最も大きい値は \( 209-30=179 \) 分なので,\( 180 \) 分未満になります。
【正しくない理由】
➁ ・・・ \( 40 \) 人に対して調査したときの第1四分位数は,値の小さい方から \( 10 \) 番目と
\( 11 \) 番目の値の平均値になります。
\( 30 \) 分以上 \( 60 \) 分未満の度数は \( 3 \) 人,\( 60 \) 分以上 \( 90 \) 分未満の
累積度数は \( 12 \) 人であることから,値の小さい方から \( 10 \) 番目と \( 11 \) 番目の値は,
どちらも \( 60 \) 分以上 \( 90 \) 分未満の階級に含まれています。
\( 60 \) 分以上 \( 90 \) 分未満の階級の階級値は,\( \dfrac{60+90}{2}=75 \) 分になります。
➂ ・・・ \( 120 \) 分未満の累積度数は \( 3+9+7=19 \) 人になります。
大問2
(1) ある学校の生徒,職員から5人を選び,年齢順に若い方からA,B,C,D,Eとする。5人の年齢の中央値は \( 30 \) 歳である。【Aの年齢を \( 3 \) 倍し \( 2 \) を加えると,Dの年齢と等しくなる】。また,BとEの年齢の和は \( 78 \) 歳であり,5人の年齢の平均値はちょうど \( 34 \) 歳である。
このとき,(ア)~(ウ)の各問いに答えなさい。
(ア) Cの年齢を答えなさい。
【解説】
全部で5人のデータを集計しているので,中央値は若い方から3番目の人,つまり,Cの年齢になります。
よって,Cの年齢は \( 30 \) 歳になります。
(イ) Aの年齢を \( x \) 歳,Dの年齢を \( y \) 歳とする。このとき,\( x、y \) を用いて【 】部の関係を等式に表しなさい。
【解説】
Aの年齢(\( x \))を \( 3 \) 倍し \( 2 \) を加えると,Dの年齢(\( y \))と等しくなるので,
\( y=3x+2 \)
(ウ) AとDの年齢を答えなさい。
【解答】
Aの年齢 ・・・ \( 15 \) 歳
Dの年齢 ・・・ \( 47 \) 歳
【解説】
Aの年齢を \( x \) 歳,Bの年齢を \( l \) 歳,Cの年齢を \( m \) 歳,Dの年齢を \( y \) 歳,
Eの年齢を \( n \) 歳とすると,5人の年齢の平均値は \( \dfrac{x+l+m+y+n}{5} \) で求めることができます。
(ア)より,Cの年齢は \( 30 \) 歳なので,\( m=30 \),
問題より,BとEの年齢の和は \( 78 \) 歳なので,\( l+n=78 \),
であり,
\( \dfrac{x+l+m+y+n}{5}=34 \)
\( x+l+m+y+n=170 \)
\( x+y+30+78=170 \)
\( x+y=62 \)
(ア)より,\( y=3x+2 \) なので,
\( x+(3x+2)=62 \)
\( 4x=60 \)
\( x=15 \)
\( y=3x+2 \) に代入すると,
\( y=3 \times 15+2=47 \)
よって,Aの年齢は \( 15 \) 歳,Dの年齢は \( 47 \) 歳になります。
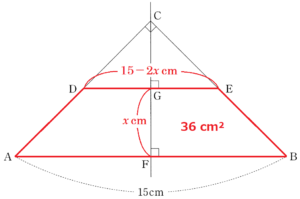
(2) 下の図のように,\( AB=15 \; cm,AC=BC \) の直角二等辺三角形 \( ABC \) があり,辺 \( AC \) 上に点 \( D \),辺 \( BC \) 上に点 \( E \) を,\( AB//DE \) となるようにとる。また,頂点 \( C \) を通る直線 \( AB \) の垂線をひき,その垂線と2つの線分 \( AB,DE \) との交点をそれぞれ \( F,G \) とする。
このとき,(ア)~(ウ)の各問いに答えなさい。
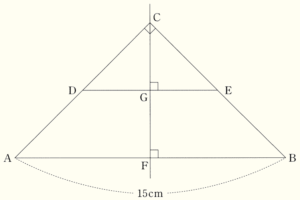
(ア) 線分 \( CF \) の長さを求めなさい。
【解答】
\( CF=\dfrac{15}{2} \; cm \)
【解説】
\( △CAF \) と \( △CBF \) において,
\( △ABC \) は直角二等辺三角形なので,\( AC=BC,∠CAF=∠CBF=45° \)
仮定より \( CF⊥AB \) なので,\( ∠CFA=∠CFB=90° \)
ここから,斜辺と他の1鋭角が等しい直角三角形なので,\( △CAF≡△CBF \) になっています。
\( △CAF \) は \( CF=AF \) の直角二等辺三角形,
\( △CBF \) は \( CF=BF \) の直角二等辺三角形なので,
\( CF=AF=BF \) になっています。
よって, \( AF+BF=AB=15 \; cm \) なので,
\( CF=AF=BF=\dfrac{15}{2} \; cm \)
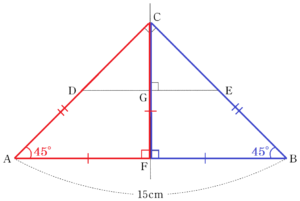
(イ) 線分 \( FG \) の長さを \( x \; cm \) とするとき,線分 \( DE \) の長さを \( x \) を用いて表しなさい。
【解説】
\( AB//DE \) より,\( ∠CDE=∠CAB,∠CED=∠CBA \) なので,
\( △CDE \) ∽ \( △CAB \) になっています。
\( △CDE \) において,線分 \( DE \) を底辺とするとき,線分 \( CG \) は高さ,
\( △CAB \) において,線分 \( AB \) を底辺とするとき,線分 \( CF \) は高さ
と考えることができます。
相似な三角形において,高さの比は相似比と等しくなるので,\( CG:CF=DE:AB \)
(ア)より、\( CF=\dfrac{15}{2} \; cm \) なので,
\( CG \) の長さは \( CG=CF-GF=\dfrac{15}{2}-x \; cm \) と表すことができます。
よって,
\( CG:CF=DE:AB \)
\( \left( \dfrac{15}{2}-x \right):\dfrac{15}{2}=DE:15 \)
\( (15-2x):15=DE:15 \)
\( DE=15-2x \; (cm) \)
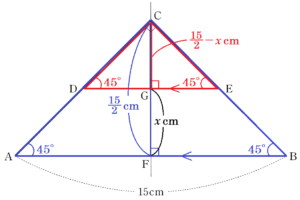
(ウ) 四角形 \( ABED \) の面積が \( 36 \; cm^2 \) であるとき,線分 \( FG \) の長さを求めなさい。
ただし、線分 \( FG \) の長さを \( x \; cm \) として,\( x \) についての方程式をつくり,答えを求めるまでの過程も書きなさい。
【解答】
四角形 \( ABED \) の面積が \( 36 \; cm^2 \) なので,
\( \dfrac{1}{2}x\{ (15-2x)+15 \}=36 \)
\( x(30-2x)=72 \)
\( 2x^2-30x+72=0 \)
\( x^2-15x+36=0 \)
\( (x-3)(x-12)=0 \)
\( x=3,12 \)
\( 0≦x≦\dfrac{15}{2} \) より,
あてはまる \( x \) の値は \( x=3 \)
よって,線分 \( FG \) の長さは \( 3 \; cm \)
【解説】
\( AB//DE,CF⊥AB \) より,四角形 \( ABED \) は台形になっています。
大問3
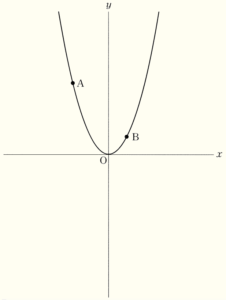
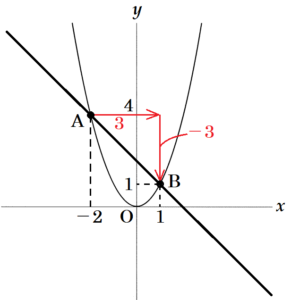
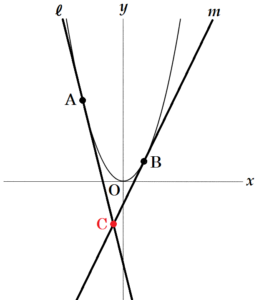
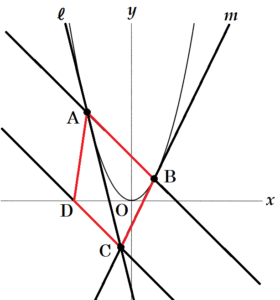
下の図のように,関数 \( y=x^2 \) のグラフ上に2点 \( A,B \) があり,点 \( A \) の \( x \) 座標は \( -2 \),点 \( B \) の \( x \) 座標は \( 1 \) である。また,点 \( A \) を通り傾き \( -4 \) の直線を ℓ,点 \( B \) を通り傾き \( 2 \) の直線を \( m \) とし,2直線 ℓ\( ,m \) の交点を \( C \) とする。さらに,点 \( C \) を通り2点 \( A,B \) を通る直線に平行な直線を \( n \) とする。
このとき,次の(1)~(6)の各問いに答えなさい。
(1) 点 \( A \) の \( y \) 座標を求めなさい。
【解説】
点 \( A \) は \( y=x^2 \) 上の点で,
\( x \) 座標は \( -2 \) なので,
\( y=(-2)^2=4 \)
(2) 2点 \( A,B \) を通る直線の傾きを求めなさい。
【解説】
点 \( B \) は \( y=x^2 \) 上の点で,
\( x \) 座標は \( 1 \) なので,
\( y=1^2=1 \)
\( A(-2,4),B(1,1) \) を通る直線の傾きは,
\( \dfrac{1-4}{1-(-2)}=-1 \)
(3) 直線 ℓ の式を求めなさい。
【解説】
直線 ℓ は \( A(-2,4) \) を通り傾き \( -4 \) の直線なので,
直線 ℓ の式を \( y=-4x+b \) とし,\( x=-2,y=4 \) を代入すると,
\( 4=-4 \times (-2)+b \)
\( b=-4 \)
よって,直線 ℓ の式は \( y=-4x-4 \)
(4) 点 \( C \) の座標を求めなさい。
【解答】
\( C \left( -\dfrac{1}{2},-2 \right) \)
【解説】
直線 \( m \) は \( B(1,1) \) を通り傾き \( 2 \) の直線なので,
直線 \( m \) の式を \( y=2x+d \) とし,\( x=1,y=1 \) を代入すると,
\( 1=2 \times 1+d \)
\( d=-1 \)
よって,直線 \( m \) の式は \( y=2x-1 \)
点 \( C \) は2直線 ℓ\( ,m \) の交点で,
交点の座標は2つの連立方程式の解として
表れるので,
\( \left\{ \begin{array}{}
y=-4x-4 \;\; ・・・ \;\; ➀ \\
y=2x-1 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
\( -4x-4=2x-1 \)
\( 6x=-3 \)
\( x=-\dfrac{1}{2} \)
➁に代入すると,
\( y=2 \times \left( -\dfrac{1}{2} \right)-1=-2 \)
よって,点 \( C \) の座標は \( C\left( -\dfrac{1}{2},-2 \right) \)
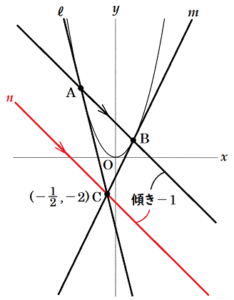
(5) 直線 \( n \) の式を求めなさい。
【解答】
\( y=-x-\dfrac{5}{2} \)
【解説】
平行な直線の傾きは等しくなります。
直線 \( n \) は2点 \( A,B \) を通る直線と平行なので,
(2)より,直線 \( n \) の傾きは \( -1 \) です。
直線 \( n \) の式を \( y=-x+e \) とすると,
\( C\left( -\dfrac{1}{2},-2 \right) \) を通るので,
\( -2=-\left( -\dfrac{1}{2} \right)+e \)
\( e=-\dfrac{5}{2} \)
よって,直線 \( n \) の式は \( y=-x-\dfrac{5}{2} \)
(6) 直線 \( n \) と \( x \) 軸との交点を \( D \) とするとき,四角形 \( ADCB \) の面積を求めなさい。
【解説】
四角形 \( ADCB \) は全体的に斜めになっていて
そのまま面積を計算するのは面倒なので,
\( △ACD \) と \( △ACB \) にわけて面積を求めます。
【\( △ACD \) の面積を求める】
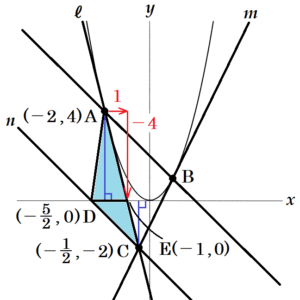
直線 ℓ と \( x \) 軸との交点を \( E \) とすると,\( △ACD=△ADE+△CDE \) と考えることができます。
点 \( D \) は \( y=-x-\dfrac{5}{2} \) 上の点で,
\( y \) 座標は \( 0 \) なので,
\( 0=-x-\dfrac{5}{2} \)
\( x=-\dfrac{5}{2} \)
であり,点 \( D \) の \( x \) 座標は \( -\dfrac{5}{2} \)
点 \( E \) は直線 ℓ 上の点であり,
直線 ℓ は \( A(-2,4) \) を通り傾きが \( -4 \) なので,
\( y \) 座標が \( 0 \) になるのは
点 \( A \) から \( x \) 軸方向に \( 1 \) 進んだときなので,
そのときの \( x \) 座標は \( -1 \)
\( △ADE \) と \( △CDE \) の底辺を線分 \( DE=\dfrac{3}{2} \) と考えると,
\( △ACD \) の面積は,
\( △ACD=△ADE+△CDE \)
\( =\left( \dfrac{3}{2} \times 4 \times \dfrac{1}{2} \right)+\left( \dfrac{3}{2} \times 2 \times \dfrac{1}{2} \right) \)
\( =3+\dfrac{3}{2} \)
\( =\dfrac{9}{2} \)
【\( △ACB \) の面積を求める】
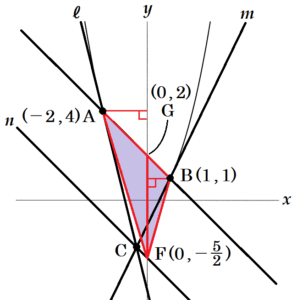
直線 \( n \) と \( y \) 軸との交点を \( F \) とすると,直線 \( n \) は直線 \( AB \) と平行なので,
等積変形の考え方から,\( △ACB=△AFB \) になっています。
また,直線 \( AB \) と \( y \) 軸との交点を \( G \) とすると,\( △AFB=△AFG+△BFG \) と考えることができます。
点 \( F \) は \( y=-x-\dfrac{5}{2} \) と \( y \) 軸の交点なので,
点 \( F \) の \( y \) 座標は \( -\dfrac{5}{2} \)
点 \( G \) は直線 \( AB \) 上の点で,
直線 \( AB \) の式を \( y=-x+f \) とすると,
\( B(1,1) \) を通るので,
\( 1=-1+f \)
\( f=2 \)
であり,点 \( G \) の \( y \) 座標は \( 2 \)
\( △AFG \) と \( △BFG \) の底辺を線分 \( FG=\dfrac{9}{2} \) と考えると,
\( △AFB \) の面積は,
\( △AFB=△AFG+△BFG \)
\( =\left( \dfrac{9}{2} \times 2 \times \dfrac{1}{2} \right)+\left( \dfrac{9}{2} \times 1 \times \dfrac{1}{2} \right) \)
\( =\dfrac{9}{2}+\dfrac{9}{4} \)
\( =\dfrac{27}{4} \)
であり,\( △ACB=△AFB=\dfrac{27}{4} \)
以上より,四角形 \( ADCB \) の面積は,
四角形 \( ADCB=△ACD+△ACB \)
\( =\dfrac{9}{2}+\dfrac{27}{4} \)
\( =\dfrac{45}{4} \)
大問4
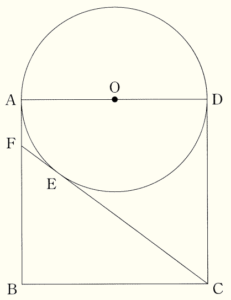
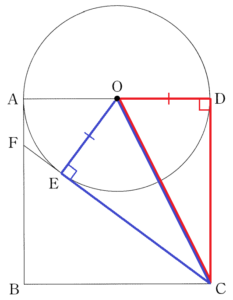
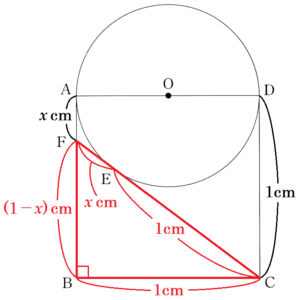
下の図のように,1辺の長さが \( 1 \; cm \) の正方形 \( ABCD \) があり,辺 \( AD \) を直径とし,点 \( O \) を中心とする円 \( O \) がある。点 \( C \) から円 \( O \) に接線をひき,点 \( D \) でない接点を \( E \) とし,接線 \( CE \) と辺 \( AB \) との交点を \( F \) とする。
このとき,次の(1)~(4)の各問いに答えなさい。
(1) \( ∠OEC \) の大きさを求めなさい。
【解説】
円の半径 \( OE \) と接線 \( CE \) は接点 \( E \) において
垂直に交わるので,\( ∠OEC=90° \)
(2) \( △OCD≡△OCE \) であることを証明しなさい。
【解答】
\( △OCD \) と \( △OCE \) において,
正方形の内角なので,\( ∠ODC=90° \) ・・・ ➀
点 \( E \) は,円 \( O \) と線分 \( CF \) の接点なので,
\( ∠OEC=90° \) ・・・ ➁
➀➁より \( ∠ODC=∠OEC=90° \) ・・・ ➂
円 \( O \) の半径なので,\( OD=OE \) ・・・ ➃
また,線分 \( OC \) は共通 ・・・ ➄
➂➃➄より,
斜辺と他の1辺がそれぞれ等しい直角三角形なので,
\( △OCD≡△OCE \)
(3) 線分 \( AF \) の長さを求めなさい。
【解答】
\( AF=\dfrac{1}{4} \; cm \)
【解説】
この問題では,長さは正方形の1辺の長さ \( 1 \; cm \) しかわかっていないし,
角度も,正方形の内角である \( 90° \) と半径と接線のなす角度 \( 90° \) しかわかっていないため,
線分 \( AF \) の長さを直接求めるには情報が足りません。
ここから,線分 \( AF \) の長さを \( x \; cm \) とすると,
\( BF=(1-x) \; cm,CF=(x+1) \; cm \)
と表すことができるので,三平方の定理を \( x \) を使った式で表すことで,
\( x \) の値を求めることができます。
\( AF=x \; cm \) とすると,
\( BF=AB-AF=(1-x) \; cm \)
点 \( F \) を通る円 \( O \) の接線なので,
\( AF=EF=x \; cm \)
点 \( C \) を通る円 \( O \) の接線なので,
\( CE=CD=1 \; cm \)
であり,
\( CF=CE+EF=(x+1) \; cm \)
ここから,\( △BCF \) において,三平方の定理より,
\( CF^2=BF^2+BC^2 \)
\( (x+1)^2=(1-x)^2+1^2 \)
\( x^2+2x+1=x^2-2x+2 \)
\( x=\dfrac{1}{4} \; (cm) \)
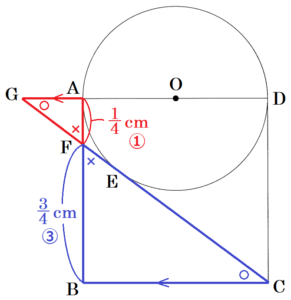
(4) 直線 \( AD \) と直線 \( CF \) の交点を \( G \) とする。\( △AGF \) の面積を \( S,△BCF \) の面積を \( T \) とするとき,\( S:T \) を最も簡単な整数の比で表しなさい。
【解説】
\( △AGF \) と \( △BCF \) において,
正方形の向かい合う辺は平行なので,
\( GD//BC \) であり,
錯角は等しいので,\( ∠AGF=∠BCF \) ・・・ ➀
対頂角は等しいので,\( ∠AFG=∠BFC \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △AGF \) ∽ \( △BCF \)
(3)より \( AF=\dfrac{1}{4} \; cm \) であることから,
\( BF=\dfrac{3}{4} \; cm \) なので,相似比は \( 1:3 \)
相似な三角形の面積比は相似比の2乗の比と等しいので,
\( S:T=1^2:3^2=1:9 \)
大問5
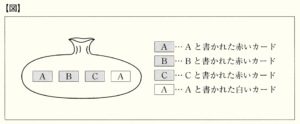
(1) 下の【図】のように,A,B,Cと書かれた赤いカードがそれぞれ1枚ずつと,Aと書かれた白いカードが1枚入っている袋がある。この袋の中から,カードを1枚ずつ続けて3回取り出し,取り出した順に左から横1列に並べる。
このとき,(ア)~(ウ)の各問いに答えなさい。
ただし,これらのカードの取り出し方は同様に確からしいとし,取り出したカードは袋にもどさないこととする。
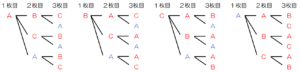
(ア) 取り出した3枚のカードの並べ方は,全部で何通りあるか求めなさい。
【解説】
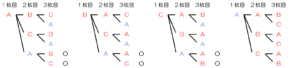
取り出した3枚のカードの並べ方を樹形図を使って表すと,下の図のようになります。
(赤いカードを
A,
B,
C ,白いカードを
A と表しています。)
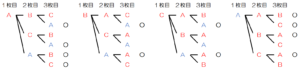
(イ) 並べた3枚のカードの中に,Aと書かれたカードが2枚含まれる確率を求めなさい。
【解説】
(ア)の樹形図の中で,Aと書かれたカードが2枚含まれている組み合わせに「〇」をつけると
すべての組み合わせは \( 24 \) 通り,Aと書かれたカードが2枚含まれている組み合わせは \( 12 \) 通り
なので,求める確率は \( \dfrac{12}{24}=\dfrac{1}{2} \)
(ウ) 並べた3枚のカードの色が,左から順に赤,白,赤となる確率を求めなさい。
【解説】
(ア)の樹形図の中で,左から順に赤,白,赤となる組み合わせに「〇」をつけると
すべての組み合わせは \( 24 \) 通り,左から順に赤,白,赤となる組み合わせは \( 6 \) 通り
なので,求める確率は \( \dfrac{6}{24}=\dfrac{1}{4} \)
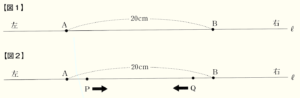
(2) 【図1】のように,直線 ℓ 上に2点 \( A,B \) があり,\( AB=20 \; cm \) である。はじめ点 \( P \) は点 \( A \) の位置に,点 \( Q \) は点 \( B \) の位置にあり,【図2】のように,スタートの合図と同時に直線ℓ上を,点 \( P \) は点 \( A \) から右へ毎秒 \( 1 \; cm \),点 \( Q \) は点 \( B \) から左へ毎秒 \( 1 \; cm \) の速さで動き始める。
ただし,2点 \( P,Q \) は止まることなく一定の速さで,動き続ける。
このとき,(ア)~(ウ)の各問いに答えなさい。
(ア) スタートの合図から \( 3 \) 秒後の線分 \( PQ \) の長さを求めなさい。
【解説】
スタートの合図から \( 3 \) 秒後には,\( AP=BQ=3 \; cm \) になっているので,
\( PQ=20-(3+3)=14 \; (cm) \)

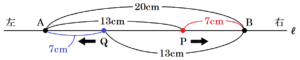
(イ) スタートの合図から \( 13 \) 秒後の線分 \( PQ \) の長さを求めなさい。
【解説】
スタートの合図から \( 13 \) 秒後には,\( AP=BQ=13 \; cm \),
つまり,\( AQ=PB=7 \; cm \)になっているので,
\( PQ=20-(7+7)=6 \; (cm) \)
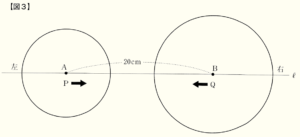
(ウ) 【図3】のような点 \( P \) を中心とする半径 \( 6 \; cm \) の円 \( P \) と,点 \( Q \) を中心とする半径 \( 8 \; cm \) の円 \( Q \) を考える。円 \( Q \) の半径は,スタートの合図と同時に毎秒 \( 1 \; cm \) ずつ大きくなっていく。
ただし,円 \( P \) の半径は変わらない。
このとき,2つの円 \( P,Q \) の半径の差と線分 \( PQ \) の長さが等しくなるのは,スタートの合図から何秒後であるか,すべて求めなさい。
【解答】
\( 6 \) 秒後,\( 22 \) 秒後
【解説】
スタートの合図から \( x \) 秒後の円 \( Q \) の半径は,\( x+8 \; cm \) と表すことができるので,
\( x \) 秒後の円 \( P,Q \) の半径の差は \( (x+8)-6=x+2 \; (cm) \) と表すことができます。
次に,\( x \) 秒後の \( PQ \) の長さを \( x \) を使った式で表していきます。
【 \( 0≦x≦10 \) の場合】
(ア)より,スタートの合図から \( x \) 秒後には,\( AP=BQ=x \; cm \) になっているので,
\( x \) 秒後の \( PQ \) の長さは \( PQ=20-(x+x)=20-2x \; (cm) \) と表すことができます。
よって,円 \( P,Q \) の半径の差と等しくなるのは,
\( x+2=20-2x \)
\( x=6 \; (cm) \)
【 \( 10≦x≦20 \) の場合】
(イ)より,スタートの合図から \( x \) 秒後には,\( AQ=PB=20-x \; cm \) になっているので,
\( x \) 秒後の \( PQ \) の長さは \( PQ=20-\{(20-x)+(20-x)\}=2x-20 \; (cm) \) と表すことができます。
よって,円 \( P,Q \) の半径の差と等しくなるのは,
\( x+2=2x-20 \)
\( x=22 \; (cm) \)
これは \( 10≦x≦20 \) の範囲に含まれていないのであてはまりません。
【 \( 20≦x \) の場合】
スタートの合図から \( x \) 秒後には,\( AQ=PB=x-20 \; cm \) になっているので,
\( x \) 秒後の \( PQ \) の長さは \( PQ=20+\{(x-20)+(x-20)\}=2x-20 \; (cm) \) と表すことができます。
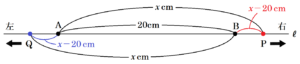
よって,円 \( P,Q \) の半径の差と等しくなるのは,
\( x+2=2x-20 \)
\( x=22 \; (cm) \)
以上より,あてはまる \( x \) の値は,\( x=6,22 \) になります。