大問1
(1) \( (-4) \times 2 \) を計算しなさい。
(2) \( 5\sqrt{3}- \sqrt{27} \) を計算しなさい。
【解説】
\( =5\sqrt{3}-3\sqrt{3} \)
\( =2\sqrt{3} \)
(3) 二次方程式 \( x^2-14x+49=0 \) を解きなさい。
【解説】
\( (x-7)^2=0 \)
\( (x-7)=0 \)
\( x=7 \)
(4) \( y \) は \( x \) に比例し、\( x=-2 \) のとき \( y=10 \) である。\( x \) と \( y \) の関係を式に表しなさい。
【解説】
\( y \) は \( x \) に比例するということは,式に表すと,\( y=ax \) の形になります。
ここに,\( x=-2,y=10 \) を代入すると,
\( 10=a \times (-2) \)
\( a=-5 \)
よって,求める式は,\( y=-5x \) になります。
(5) 関数 \( y=\dfrac{1}{4}x^2 \) について、 \( x \) の値が \( 2 \) から \( 6 \) まで増加するときの変化の割合を求めなさい。
【解説】
変化の割合は次の式で求めることができます。
変化の割合 \(=\dfrac{y の変化量}{x の変化量} \)
\( x=2 \) のとき,\( y \) の値は,\( y=\dfrac{1}{4} \times2^2=1 \)
\( x=6 \) のとき,\( y \) の値は,\( y=\dfrac{1}{4} \times6^2=9 \)
なので,
変化の割合 \(=\dfrac{9-1}{6-2}=2 \)
(6) 赤玉3個,白玉2個,青玉1個がはいっている箱から,同時に2個の玉を取り出すとき,取り出した2個の玉の色が異なる確率を求めなさい。ただし,どの玉の取り出し方も,同様に確からしいものとする。
【解答】
\( \dfrac{11}{15} \)
【解説】
球の取り出し方を樹形図にして色が異なるところに
○を書いてみます。
すべての場合の数は15通りで,色が異なるのは11通りなので,
求める確率は \( \dfrac{11}{15} \)

(7) ある式に \( 3a-5b \) をたす計算を間違えて,ある式から \( 3a-5b \) をひいてしまったために,答えが \( -2a+4b \) となった。正しく計算をしたときの答えを求めなさい。
【解説】
「ある式」を A とすると,
「ある式」から \( 3a-5b \) をひいた答えが \( -2a+4b \) となったのだから,
A \( -(3a-5b)=-2a+4b \)
A \( =-2a+4b+3a-5b \)
\( =a-b \)
「ある式」に \( 3a-5b \) をたすと,
A \( +(3a-5b)=a-b+3a-5b \)
\( =4a-6b \)
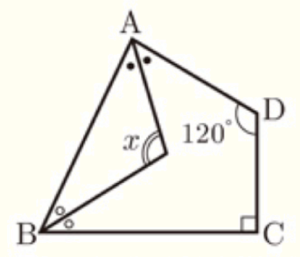
(8) 右の図のように,\( ∠C=90°,∠D=120° \) の四角形 \( ABCD \) がある。同じ印をつけた角の大きさが等しいとき,\( ∠x \) の大きさを求めなさい。
【解説】
四角形の内角の和は \( 360° \) なので,
\( ∠ABC+∠BAD+120°+90°=360° \)
\( ∠ABC+∠BAD=150° \)
\( ○+○+●+●=150° \)
\( 2(○+●)=150° \)
\( ○+●=75° \)
内側の三角形において,
\( ∠x+○+●=180° \)
\( ∠x+75°=180° \)
\( ∠x=105° \)
(9) 1から9までの9つの自然数から異なる4つの数を選んでその積を求めると,810になった。この4つの数をすべて書きなさい。
【解説】
810を素因数分解すると,
\( 810=2 \times 3 \times 3 \times 3 \times 3 \times 5 \)
\( =(2 \times 3) \times (3 \times 3) \times 3 \times 5 \)
\( =6 \times 9 \times 3 \times 5 \)
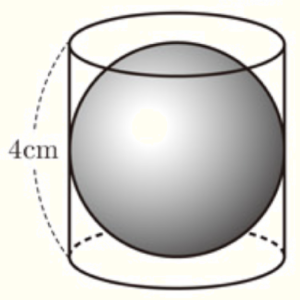
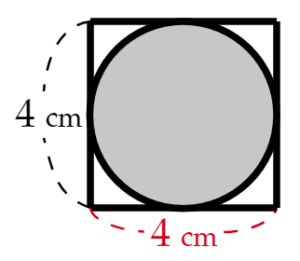
(10) 右の図のように,円柱と,その中にちょうどはいる球がある。円柱の高さが \( 4 \; cm \) であるとき,円柱の体積と球の体積の差を求めなさい。ただし,円周率は \( \pi{} \) とする。
【解答】
\( \dfrac{16}{3}\pi{} \; cm^3 \)
【解説】
球は,円柱の中にちょうどはいるので,正面から見ると右の図のようになります。
球の高さと円柱の高さは等しいので,\( 4\; cm \)
左右も接しているので,円柱の底面は直径 \( 4\; cm \) の円であるとわかります。
円柱の体積 \( =\pi{} \times 2^2 \times 4=16\pi{} \; (cm^3) \)
球の体積 \( =\dfrac{4}{3} \times \pi{} \times 2^3=\dfrac{32}{3}\pi{} \; (cm^3) \)
なので,体積の差は,
\( 16\pi{}-\dfrac{32}{3}\pi{}=\dfrac{16}{3}\pi{} \; (cm^3) \)
大問2
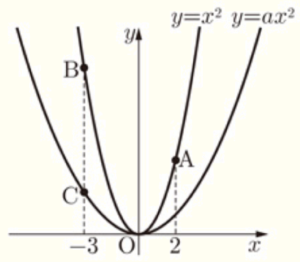
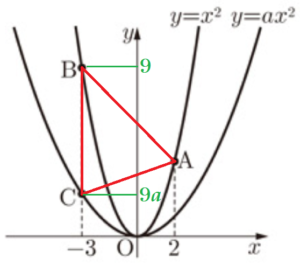
右の図のように,2つの関数 \( y=x^2 \) と \( y=ax^2 (0<a<1) \) のグラフがある。関数 \( y=x^2 \) のグラフ上に2点 \( A,B \),関数 \( y=ax^2 \) のグラフ上に点 \( C \) があり,点 \( A \) の \( x \) 座標は \( 2 \),点 \( B,C \) の \( x \) 座標は \( -3 \) である。(1)~(4) に答えなさい。
(1) 関数 \( y=x^2 \) のグラフと \( x \) 軸について線対称となるグラフの式を求めなさい。
【解説】
関数 \( y=ax^2 \) のグラフと \( x \) 軸について線対称となるグラフの式は,\( y=-ax^2 \) になります。
よって,求める式は,\( y=-x^2 \)
(2) 2点 \( A,B \) を通る直線の式を求めなさい。
【解説】
2点 \( A,B \) の \( y \) 座標は,
\( A \) ・・・ \( y=2^2=4 \)
\( B \) ・・・ \( y=(-3)^2=9 \)
なので,2点 \( (-3,9),(2,4) \) を通る直線の式は,
傾き \( =\dfrac{4-9}{2-(-3)}=-1 \)
この直線の式を \( y=-x+b \) とし,\( (2,4) \) を代入すると,
\( 4=-2+b \)
\( b=6 \)
以上より,求める直線の式は,\( y=-x+6 \)
(3) \( △ABC \) の面積を \( a \) を用いて表しなさい。
【解答】
\( \dfrac{45-45a}{2} \)
【解説】
点 \( B,C \) の \( x \) 座標は \( -3 \) なので,\( y \) 座標の値は,
\( B \) ・・・ \( y=(-3)^2=9 \)
\( C \) ・・・ \( y=a \times (-3)^2=9a \)
なので,線分 \( BC \) の長さは,\( 9-9a \)
線分 \( BC \) を底辺とすると,高さは \( 2-(-3)=5 \)
よって,
\( △ABC=(9-9a) \times 5 \times \dfrac{1}{2} \)
\( =\dfrac{45-45a}{2} \)
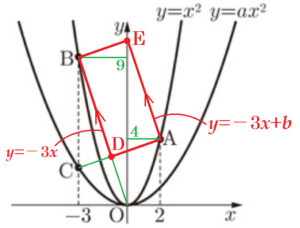
(4) 線分 \( AC \) と線分 \( OB \) との交点を \( D \) とし,点 \( E \) を \( y \) 軸上にとる。四角形 \( BDAE \) が平行四辺形となるとき, \( a \) の値を求めなさい。
【解答】
\( a=\dfrac{7}{27} \)
【解説】
点 \( B \) の座標は \( (-3,9) \) なので,線分 \( OB \) の式は \( y=-3x \)
平行四辺形の向かい合う辺は平行なので,線分 \( AE \) の式は \( y=-3x+b \) と表すことができます。
この直線は \( A(2,4) \) を通るので,
\( 4=-3 \times 2+b \)
\( b=10 \)
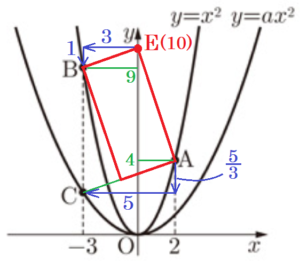
よって,\( E \) の座標は,\( E(0,10) \)
点 \( E \) から点 \( B \) までは
\( x \) 軸方向に \( -3 \),\( y \) 軸方向に \( -1 \) 進むので,
点 \( A \) から点 \( C \)までは
\( x \) 軸方向に \( -5 \) 進むので,\( y \) 軸方向に \( -\dfrac{5}{3} \) 進みます。
よって,点 \( C \) の座標は,\( C \left(-3,\dfrac{7}{3} \right) \)
\( y=ax^2 \) に代入すると,
\( \dfrac{7}{3}=a \times (-3)^2 \)
\( a=\dfrac{7}{27} \)
大問3
ゆうきさんとひかるさんは,桜の開花日予想に興味をもち,数学の授業で学んだことを利用して,今年の桜の開花日を予想しようと話し合っている。(1)・(2)に答えなさい。
【話し合いの一部】
ゆうきさん 気象庁のホームページには,徳島県の桜の開花日のデータがあります。
それを使って過去40年間の桜の開花日をヒストグラムに表すと,図1のようになりました。
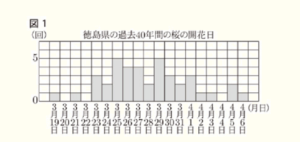
ひかるさん 開花日が4月1日以降になった年が, ( ① ) 回ありますね。
ゆうきさん そうですね。ほかにも,3月25日から29日の5日間に開花する回数が多いことが
読みとれます。この5日間に開花した割合を求めると ( ② ) %ですね。
ひかるさん もっと開花日を正確に予想したいですね。
ゆうきさん 開花日には気温が関係しているかもしれませんね。
ひかるさん インターネットで調べてみると,気温を用いた予想方法が2つ見つかりました。
400℃の法則と600℃の法則という予想方法です。
ゆうきさん それは,どんな法則ですか。
ひかるさん どちらも2月1日を基準とする考え方です。400℃の法則は,2月1日以降その日の平均気温を
毎日たしていき,合計が400℃以上になる最初の日を開花予想日とします。600℃の法則は,
2月1日以降その日の最高気温を毎日たしていき,合計が600℃以上になる最初の日を
開花予想日とします。
ゆうきさん どちらの法則の方が正確に予想できるのでしょうか。
ひかるさん それぞれの法則で過去の開花予想日を求め,実際の開花日と比べてみましょう。
その誤差をまとめると,どちらの法則の方が正確に予想できるかを調べることができます。
ゆうきさん なるほど。気象庁のホームページには,日々の気温のデータもあります。
そのデータを用いて2022年の開花予想日を求めると,いつになりますか。
ひかるさん 平均気温の合計が400℃以上になる最初の日は,3月24日でした。
だから,400℃ の法則を使えば,開花予想日は3月24日となります。
また,600℃の法則を使えば,開花予想日は3月22日となります。
ゆうきさん 実際の開花日は3月25日だったので,400℃の法則での誤差は1日,600℃の法則での
誤差は3日ですね。
ひかるさん ほかの年ではどうなっているのでしょうか。2人で手分けして40年間分の誤差を求め,
それをヒストグラムに表して,どちらの法則の方が正確に予想できるか考えてみましょう。
(1) 【話し合いの一部】の ( ① )・( ② ) にあてはまる数を,それぞれ書きなさい。
【解答・解説】
( ① )
図1のヒストグラムから数えると,8(回)
( ➁ )
3月25日から29日の5日間に開花したのは20回,
全部で40年(40回)分の統計を取っているので,
\(\dfrac{20}{40} \times 100=50 (%) \)
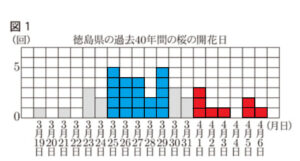
(2) 図2,図3は,40年間の気温のデータを用いて各法則で求めた開花予想日と,実際の開花日との誤差をヒストグラムに表したものである。(a)・(b)に答えなさい。ただし,誤差は絶対値で表している。
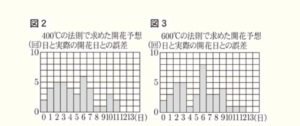
(a) この2つのヒストグラムから読みとれることとして正しいものを,ア〜エからすべて選びなさい。
ア 最頻値は,図2より図3の方が大きい。
イ 予想が的中した回数は,図2,図3とも同じである。
ウ 誤差が10日以上になる割合は,図2より図3の方が小さい。
エ 誤差が3日までの累積相対度数は,図2,図3とも同じである。
【解説】
ア 最頻値(最も度数が大きい日)は,図2,図3とも6日
イ 予想が的中した(誤差が0日の)回数は,図2,図3とも2回。
ウ 誤差が10日以上になったのは,図2 ・・・ 5回,図3 ・・・ 3回。
図2,図3とも全部で40年分の統計を取っているので,図3の方が割合は小さくなる。
エ 誤差が3日までの累積度数は,図2 ・・・ 16回,図3 ・・・ 15回。
図2,図3とも全部で40年分の統計を取っているので,図3の方が累積相対度数は小さくなる。
(b) ゆうきさんとひかるさんは,図2,図3のヒストグラムだけでは,どちらの法則の方が正確に開花日を予想できるのかを判断することが難しいと考え,箱ひげ図で比較することにした。図4は,図2,図3を作成するためにもとにしたデータを,箱ひげ図に表したものである。
ゆうきさんとひかるさんは,この2つの箱ひげ図から「400℃の法則の方が正確に開花日を予想できそうだ」と判断した。そのように判断した理由を,2つの箱ひげ図の特徴を比較して説明しなさい。
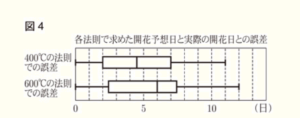
【解説】
400℃の法則の場合,中央値が4.5日なので,50%の確率で誤差が4.5日以下になっています。
600℃の法則の場合,中央値が6日なので,50%の確率で誤差が6日以下になります。
つまり,4.5日以下になる確率は50%未満であり,
400℃の法則の方がより誤差が小さく(正確に)予想できるといえます。
大問4
生徒会役員のはるきさんたちは,次の【決定事項】をもとに文化祭の日程を考えている。(1)・(2) に答えなさい。
【決定事項】
・ 文化祭は学級の出し物から始まり,学級の出し物の時間はすべて同じ長さとする。
・ 学級の出し物の間には入れ替えの時間をとり,その時間はすべて同じ長さとする。
・ すべての学級の出し物が終わった後に昼休みを60分とり,
その後,吹奏楽部の発表とグループ発表を行う。
・ グループ発表の時間はすべて同じ長さとする。
・ 昼休み以降の発表の間には,入れ替えの時間をとらず,発表の時間に含める。
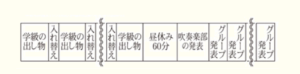
(1) はるきさんたちは,次の【条件】をもとに文化祭のタイムスケジュールをたてることにした。(a)・(b) に答えなさい。
【条件】
・ 学級の出し物を5つ,グループ発表を10グループ とする。
・ 学級の出し物の時間は,入れ替えの時間の4倍とし,吹奏楽部の発表の時間を40分とする。
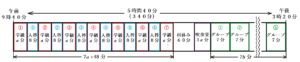
・ 最初の学級の出し物が午前10時に始まり,最後の学級の出し物が正午に終わるようにする。
・ 最後のグループ発表が午後3時に終わるようにする。
(a) 学級の出し物の時間と入れ替えの時間は,それぞれ何分か,求めなさい。
【解答】
学級の出し物の時間 ・・・ 20分
入れ替えの時間 ・・・ 5分
【解説】
学級の出し物の時間を \( x \) 分,入れ替えの時間を \( y \) 分とすると,
午前10時から正午までの2時間(=120分)に学級の出し物が5つあって,入れ替えの時間は4回あるので,
\( 5x+4y=120 \) ・・・ ①
学級の出し物の時間は,入れ替えの時間の4倍なので,
\( x=4y \) ・・・ ➁
①➁を連立方程式として解くと,
\( x=20,y=5 \)
【連立方程式の途中式】
\( \left\{
\begin{array}{}
5x+4y=120 \\
x=4y
\end{array}
\right. \)
➁を①に代入
\( 5x+x=120 \)
\( 6x=120 \)
\( x=20 \)
➁に代入
\( 20=4y \)
\( y=5 \)
(b) グループ発表の時間は何分か,求めなさい。
【解説】
正午から,昼休みが60分,吹奏楽部の発表が40分あるので,
グループ発表が始まるのは午後1時40分。
ここから,午後3時までの1時間20分(=80分)の間にグループ発表を10個行うので,
グループ発表の時間は,\( 80 \div 10=8 \) (分)
(2) はるきさんたちは,学級の出し物の数を変更し,条件を見直すことにした。次の【見直した条件】をもとに,受け付けできるグループ発表の数について検討をしている。(a)・(b) に答えなさい。
【見直した条件】
・ 学級の出し物は7つとし,学級の出し物の入れ替えの時間は8分とする。
・ 吹奏楽部の発表の時間は,学級の出し物の時間の3倍とする。
・ グループ発表の時間は7分とする。
・ 最初の学級の出し物が午前9時40分に始まる。
・ 最後のグループ発表が午後3時20分までに終わる。
(a) 最後のグループ発表が午後3時20分ちょうどに終わるとき,学級の出し物の時間を \( a \) 分,グループ発表の数を \( b \) グループとして,この数量の関係を等式で表しなさい。
【解説】
1つ \( a \) 分の学級の出し物を7つ行うときにかかる時間は \( 7a \) 分
このとき,1回8分の入れ替えが6回発生するので,かかる時間は \( 48 \) 分
昼休みは60分
吹奏楽部の発表の時間は,学級の出し物の時間の3倍なので, \( 3a \) 分
1つ7分のグループ発表を \( b \) 個行うときにかかる時間は \( 7b \) 分
これらのイベントを午前9時40分から午後3時20分までの5時間40分(340分)の間に行うので,
等式で表すと,
\( 7a+48+60+3a+7b=340 \)
\( 10a+7b=232 \)
(b) 学級の出し物の時間を15分とするとき,グループ発表は,最大何グループまで受け付けできるか,求めなさい。
【解説】
(a) で導き出した等式 \( 10a+7b=232 \) より,午後3時20分までに終わらせるためには,
\( 10a+7b<232 \) が成り立つようにグループ発表のグループ数を調整すればいいことになります。
よって,\( 10a+7b<232 \) に \( a=15 \) を代入すると,
\( 10 \times 15+7b<232 \)
\( 7b<82 \)
\( b<\dfrac{82}{7}=11\dfrac{5}{7} \)
グループ数は必ず自然数になるので,最大11グループまで受け付けできる。
大問5
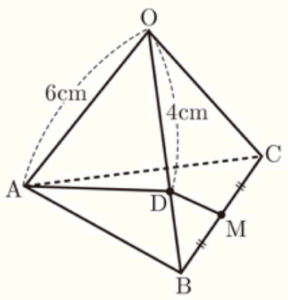
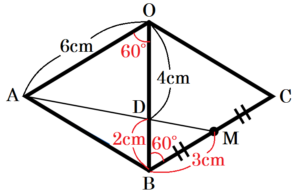
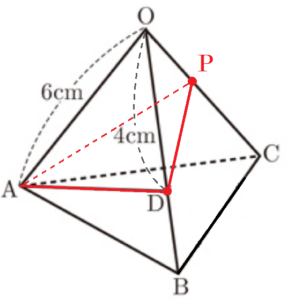
右の図のように,すべての辺の長さが \( 6 \; cm \) の正三角錐 \( OABC \) がある。辺 \( OB \) 上に点 \( D \) をとり,辺 \( BC \) の中点を \( M \) とする。\( OD=4 \; cm \) のとき, (1)~(4) に答えなさい。
(1) 正三角錐 \( OABC \) で,辺 \( AB \) とねじれの位置にある辺はどれか,書きなさい。
(2) \( △OAD \) ∽ \( △BMD \) を証明しなさい。
【解答・解説】
正三角錐のすべての面は正三角形なので,
\( ∠AOD=∠MBD=60° \) ・・・ ①
\( △OAB \) は正三角形なので,
\( OB=OA=6 \; cm \) ・・・ ②
仮定より \( OD=4 \; cm \) なので,
\( BD=OB-OD=2 \; cm \) ・・・ ➂
②➂より,\( OD:BD=4:2=2:1 \) ・・・ ➃
仮定より,
\( BM=\dfrac{1}{2}BC=3 \; cm \) ・・・ ➄
仮定より,
\( OA=6 \; cm \) ・・・ ➅
➄➅より,
\( OA:BM=6:3=2:1 \) ・・・ ➆
①④➆より,2組の辺の比とその間の角がそれぞれ等しいので,\( △OAD \) ∽ \( △BMD \)
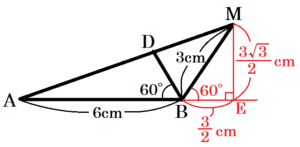
(3) \( AD+DM \) の長さを求めなさい。
【解答】
\( 3\sqrt{7} \; cm \)
【解説】
(2) より,\( △OAD \) ∽ \( △BMD \) なので,
\( ∠AOD=∠MBD \)
対頂角が等しいので,
3点 \( A,D,M \) は一直線上にあります。
点 \( M \) から辺 \( AB \) の延長線に垂線をひき,交点を点 \( E \) とすると,
\( ∠ABD=∠MBD=60° \) より,
\( ∠MBE=180°-(∠ABD+∠MBD)=60° \)
よって,\( △MBD \) は \( 30°,60°,90° \) の
直角三角形なので,
\( BE=\dfrac{1}{2}BM=\dfrac{3}{2} \; cm \)
\( EM=\dfrac{\sqrt{3}}{2}BM=\dfrac{3\sqrt{3}}{2} \; cm \)
\( △AEM \) において,三平方の定理より,
\( AM^2=EM^2+AE^2 \; cm \)
\( =\left( \dfrac{3\sqrt{3}}{2} \right)^2+\left( 6+\dfrac{3}{2} \right)^2 \)
\( =\dfrac{27}{4}+\dfrac{225}{4} \)
\( =63 \)
\( AM=3\sqrt{7} \; (cm) \)
\( AD+DM=AM=3\sqrt{7} \; (cm) \)
(4) 辺 \( OC \) 上に点 \( P \) をとる。4点 \( O,A,D,P \) を頂点とする立体 \( OADP \) の体積が正三角錐 \( OABC \) の体積の \( \dfrac{2}{7} \) 倍であるとき,線分 \( OP \) の長さを求めなさい。
【解答】
\( \dfrac{18}{7} \; cm \)
【解説】
面 \( OBC \) と面 \( ODP \) は同一平面にあるので,
これらを底面と考えると,立体 \( OADP \) と正三角錐 \( OABC \) は,
高さが共通になっています。
このとき,\( △ODP \) と \( △OBC \) の比が,
立体 \( OADP \) と正三角錐 \( OABC \) の体積比になります。
つまり,\( △ODP:△OBC=2:7 \) となるときの
線分 \( OP \) の長さを求めればいいことになります。
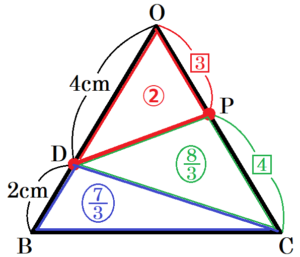
\( △OBC \) に注目すると,\( △ODP:△OBC=2:7 \) より,
\( △ODP= \) ② とするとき,\( △OBC= \) ⑦ になります。
このとき,四角形 \( BCPD=△OBC-△ODP= \) ➄ になります。
また,\( OD=4 \; cm,DB=2 \; cm \) なので,
\( △BDC:△OBC=1:3 \)
\( △BDC: \) ⑦ \( =1:3 \)
\( 3△BDC= \) ⑦
\( △BDC= \) ○\(\dfrac{7}{3}\)
注:○\(\dfrac{7}{3}\) は,\(\dfrac{7}{3}\) を○で囲んだものと考えてください。
よって,
\( △PDC= \) 四角形 \( BCPD-△BDC \)
\( = \) ➄ \( – \) ○\( \dfrac{7}{3} \)
\( = \) ○\( \dfrac{8}{3} \)
\( △ODP:△PDC= \) ②:○\( \dfrac{8}{3}=3:4 \)
\( △ODP \) と \( △PDC \) は,高さが共通なので,
\( OP:PC=△ODP:△PDC=3:4 \)
よって,
\( OP=\dfrac{3}{7}OC=\dfrac{18}{7} \; (cm) \)