鳥取県公立高校入試 令和７（2025）年度 解答＆解説
（２） \( 3\sqrt{2}+\dfrac{4}{\sqrt{2}} \)
（３） \( \dfrac{x+2y}{2}-\dfrac{x-y}{3} \)
（４） \( -\dfrac{2}{5}a^3b \div \left( -\dfrac{4}{15}ab \right) \)
問２ 次の数量を表す式を書きなさい。ただし，消費税は考えないものとする。
\( a \) 円のノートを，\( 3 \) 割引きで買ったときの代金
問３ \( 2x^2-18 \) を因数分解しなさい。
問４ 連立方程式 \( \left\{ \begin{array}{}
x+y=2 \\
3x+4y=3 \\
\end{array} \right. \) を解きなさい。
問５ 二次方程式 \( x^2-3x-1=0 \) を解きなさい。
問６ 次のア～エのうち，\( y \) が \( x \) の一次関数であるものを２つ選び，記号で答えなさい。
ア 気温 \( x \; ^\circ C \) のときの降水量 \( y \; mm \)
イ 分速 \( x \; m \) で \( 7 \) 分間進むときの道のり \( y \; m \)
ウ １辺の長さが \( x \; cm \) の正方形の面積 \( y \; cm^2 \)
エ \( 300 \; mL \) のジュースを，\( x \; mL \) 飲んだときの残り \( y \; mL \)
問７ ２つの関数 \( y=ax^2 \) と \( y=3x+2 \) について，\( x \) の値が \( 1 \) から \( 3 \) まで増加するときの，それぞれの変化の割合が等しくなるような，\( a \) の値を求めなさい。
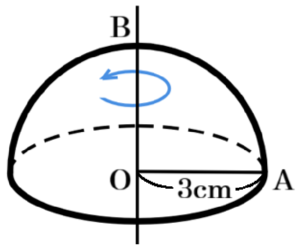
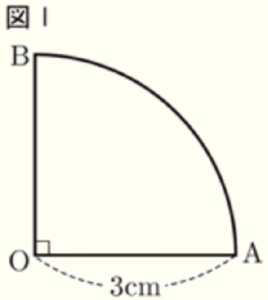
問８ 右の図Ⅰのおうぎ形 \( OAB \) について，直線 \( OB \) を回転の軸として１回転させてできる立体の体積を求めなさい。
体積は，
\( \dfrac{1}{2} \times \left( \dfrac{4}{3}\pi{} \times 3^3 \right)=\dfrac{1}{2} \times 36\pi{} \)
\( =18\pi{} \; (cm^3) \)
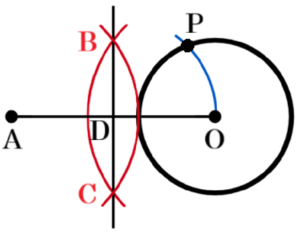
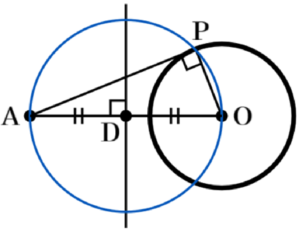
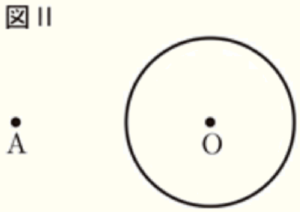
問９ 右の図Ⅱにおいて，円 \( O \) と，円 \( O \) の外部に点 \( A \) がある。次の条件を満たす点 \( P \) を作図しなさい。
ただし，作図に用いた線は明確にして，消さずに残しておき，作図した点 \( P \) には記号 \( P \) を書き入れなさい。
１ 点 \( P \) は円 \( O \) の円周上の点であり，直線 \( AO \) より上側に
ある。
２ \( ∠APO=90° \) である。
手順１ 線分 \( OA \) を描く。
手順２ ２点 \( O，A \) を中心に円弧を描く。
（交点を \( B，C \) とします。）
手順３ ２点 \( B，C \) を通る直線を描く。
（線分 \( OA \) との交点を \( D \) とします。）
手順４ 点 \( D \) を中心に線分 \( OD \) を半径とする円弧を描く。
手順４の円弧と円 \( O \) の交点が求める点 \( P \) になります。
\( ∠APO=90° \) であることから，
\( ∠APO=90° \) は，線分 \( OA \) を直径とする円
における直径 \( OA \) に対する円周角
と考えることができます。
線分 \( OA \) を直径とする円の中心は線分 \( OA \) の中点になるので，線分 \( OA \) の垂直二等分線を作図することで，この円の中心が作図できます。
この円の中心を \( D \) とすると，
点 \( P \) は円 \( D \) の円周上の点でもあり，
円 \( O \) の円周上の点でもあるので，
２つの円の交点が求める点 \( P \) になります。
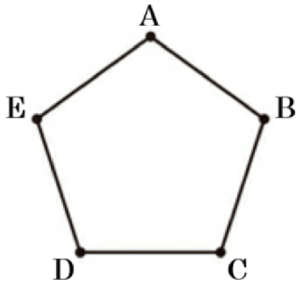
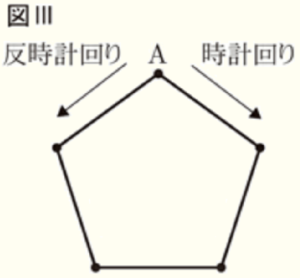
問１０ 右の図Ⅲのように正五角形があり，１つの頂点を \( A \) とする。はじめに点 \( P \) と点 \( Q \) は頂点 \( A \) の位置にある。\( 1 \) から \( 6 \) までの目がある１つのさいころを２回投げて，点 \( P \) は１回目に出た目の数だけ反時計回りに正五角形の頂点を１つずつ移動する。また，点 \( Q \) は２回目に出た目の数だけ次の【操作➀】または【操作➁】にしたがって移動する。
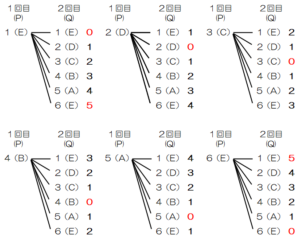
例えば，１回目に出た目の数が \( 3 \)，２回目に出た目の数が \( 6 \) であるとき，点 \( P \) と点 \( Q \) の位置は,あとの例のようになる。
【操作➀】：点 \( Q \) は２回目に出た目の数だけ反時計回りに正五角形の頂点を１つずつ移動する。
【操作➁】：点 \( Q \) は２回目に出た目の数だけ時計回りに正五角形の頂点を１つずつ移動する。
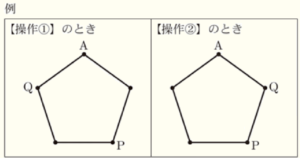
次の解答は，点 \( P \) と点 \( Q \) が移動したとき，正五角形の同じ頂点にある確率を【操作➀】の場合と【操作➁】の場合について，それぞれ求めたものである。
このとき，あとの（１），（２）に答えなさい。
ただし，さいころは６つのどの目が出ることも同様に確からしいものとする。
さいころを２回投げたときの目の出方は ア 通り。
【操作➀】のとき
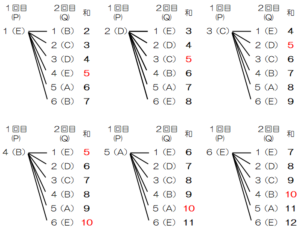
点 \( P \) と点 \( Q \) が正五角形の同じ頂点にあるときは，さいころの出た目の差が \( 0 \) か \( 5 \) となればよいので，求める確率は イ である。
【操作➁】のとき
点 \( P \) と点 \( Q \) が正五角形の同じ頂点にあるときは，さいころの出た目の ウ となればよいので，求める確率は エ である。
（１） 解答の ア ， イ にあてはまる数を，それぞれ求めなさい。
さいころを２回投げたときの目の出方は次の３６通りになります。
イ
正五角形の残りの頂点に右の図のように \( B \)～\( E \) の名前をつけます。
出た目の数とその行き先の組み合わせを樹形図にして書きだすと，差が \( 0 \) または \( 5 \) になる組み合わせは \( 8 \) 通りなので，
その確率は，\( \dfrac{8}{36}=\dfrac{2}{9} \) になります。
\( \phantom{ } \)
（２） 解答の下線部を参考にして，さいころの目の出方について ウ に適切な語句を入れなさい。
また， エ にあてはまる数を求めなさい。
点 \( P \) と点 \( Q \) の行き先が
頂点 \( A \) になる場合 ･･･ １回目に \( 5 \)，２回目も \( 5 \) の目がでたとき
頂点 \( B \) になる場合 ･･･ １回目に \( 4 \)，２回目に \( 1 \) または \( 6 \) の目がでたとき
頂点 \( C \) になる場合 ･･･ １回目に \( 3 \)，２回目に \( 2 \) の目がでたとき
頂点 \( D \) になる場合 ･･･ １回目に \( 2 \)，２回目に \( 3 \) の目がでたとき
頂点 \( E \) になる場合 ･･･ １回目に \( 1 \)，２回目に \( 4 \) の目がでたとき
なので，出た目の和が \( 5 \) か \( 10 \) になるときに同じ頂点に移動します。
エ
出た目の数とその行き先の組み合わせを樹形図にして書きだすと，
和が \( 5 \) または \( 10 \) になる組み合わせは \( 7 \) 通りなので，
その確率は，\( \dfrac{7}{36} \) になります。
大問２
次の図Ⅰは,ある中学校の３年生Ａ組 \( 30 \) 人と，Ｂ組 \( 30 \) 人のハンドボール投げの記録をそれぞれ箱ひげ図にまとめたものである。
このとき，あとの各問いに答えなさい。
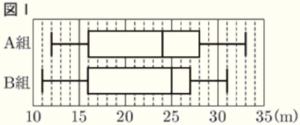
問１ Ａ組の記録の第３四分位数を求めなさい。
問２ 図Ⅰの箱ひげ図から読み取れることとして必ず正しいといえるものを，次のア～エからひとつ選び，記号で答えなさい。
ア 平均値は，Ａ組の方がＢ組より大きい。
イ 最大値は，Ａ組の方がＢ組より小さい。
ウ 範囲は，Ａ組の方がＢ組より大きい。
エ \( 29 \; m \) 以上投げた生徒の数は，Ａ組の方がＢ組より多い。
問３ Ａ組とＢ組には，運動部に所属する生徒がそれぞれ \( 15 \) 人ずついる。次の図Ⅱは，運動部に所属するＡ組 \( 15 \) 人と，Ｂ組 \( 15 \) 人のハンドボール投げの記録をそれぞれ箱ひげ図にまとめたものである。また，あとの会話は，けいたさんとかりんさんが，図Ⅱの箱ひげ図をもとに話し合ったものである。
このとき，あとの（１），（２）に答えなさい。
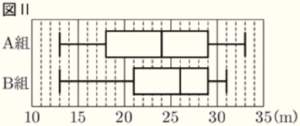
会話
けいたさん：運動部に所属する各組の生徒 \( 15 \) 人のうち，Ａ組とＢ組のどちらにハンドボールを遠くに
投げる人が多いかな。図Ⅱの箱ひげ図をみても，範囲も四分位範囲も違うからどう比べたらいいのだろう。
かりんさん：何か基準があるといいかも。先生が，この中学校の３年生で運動部に所属する生徒の
ハンドボール投げの記録の平均は，\( 25 \; m \) だとおっしゃっていたよ。
けいたさん：それでは，\( 25 \; m \) より遠くに投げた人は，Ａ組，Ｂ組のどちらの方が多いのか考えてみよう。
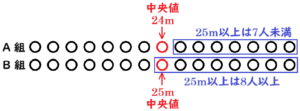
かりんさん：Ａ組は ア が \( 24 \; m \) だから，Ａ組に \( 25 \; m \) より遠くに投げた人は，最も多くて
イ 人だと考えられるね。
けいたさん：Ｂ組は ア が \( 26 \; m \) だから，Ｂ組に \( 25 \; m \) より遠くに投げた人は，少なくとも
ウ 人いるよ。
かりんさん：これで判断できるね。\( 25 \; m \) より遠くに投げた人は， エ 組の方が多いといえるね。
（１） 会話の ア にあてはまる語句を答えなさい。
ただし， ア には同じ語句があてはまるものとする。
（２） 会話の イ ， ウ にあてはまる数を求めなさい。また， エ にあてはまる組をＡ，Ｂからひとつ選び，記号で答えなさい。
大問３
問１ 次の会話Ⅰは，まなぶさんが通う学校の授業で先生が数当てマジックを披露したときのものである。
このとき，あとの（１）～（３）に答えなさい。
会話Ⅰ
先 生：\( 1 \) から \( 10 \) までの整数で好きな数をひとつ思い浮かべてください。思い浮かべたら，
次に示す手順１～４で計算をして，求めた数を教えてください。
１ はじめに思い浮かべた数を１０倍する
２ 手順１で求めた数に \( 4 \) をたす
３ 手順２で求めた数を \( 2 \) でわる
４ 手順３で求めた数から \( 12 \) をひく
まなぶさん：計算したら \( 10 \) になりました。
先 生：わかりました。まなぶさんがはじめに思い浮かべた数は \( 4 \) ですね。
まなぶさん：すごい！正解です。
先 生：どうして私が,まなぶさんのはじめに思い浮かべた数を当てることができたか考えてみて
ください。
（１） はじめに思い浮かべた数を \( n \) として，手順１～４で計算して求めた数を \( n \) を用いて式で表しなさい。
ただし，この問いの答えは，必ずしも約分や式を整理する必要はない。
（２） 手順１～４で計算して求めた数が \( 35 \) のとき，はじめに思い浮かべた数を求めなさい。
（３） 手順１～４で計算して求めた数から，はじめに思い浮かべた数を求めるための方法として適切なものを次のア～オから２つ選び，記号で答えなさい。
ア 求めた数に \( 10 \) をたし，\( 5 \) でわる。
イ 求めた数を \( 5 \) でわり，\( 10 \) をたす。
ウ 求めた数を \( 5 \) でわり，\( 2 \) をたす。
エ 求めた数を２倍し，\( 5 \) でわる。
オ 求めた数から \( 6 \) をひく。
問２ 次の会話Ⅱは，授業後にまなぶさんも数を当てる方法を自分で考え，かずこさんに披露したときのものである。
このとき，あとの（１），（２）に答えなさい。
会話Ⅱ
まなぶさん：異なる２つの自然数を選び，和と積を教えてください。
かずこさん：和は \( 14 \) で，積は \( 48 \) だよ。
まなぶさん：選んだ数は \( \boxed{ a } \) と \( \boxed{ b } \) だね。
かずこさん：正解。\( x^2+14x+48 \) を因数分解するときに考えるよね。じゃあ，もう少し難しそうな
組合せで，和が \( 22 \) で，積が \( 112 \) はどう。これならすぐわからないよね。
まなぶさん：わかるよ。かずこさんが選んだ数は \( 8 \) と \( 14 \) だね。
かずこさん：すごい！どうやって考えたの。
まなぶさん：２つの数の和の半分 \( 11 \) を基準とすれば，選んだ数のどちらかは \( 11 \) より大きく，
他方は \( 11 \) より小さくなるよね。選んだ２つの数は，\( 11+x \) と \( 11-x \) とおけて，
積は \( 112 \) だから \( (11+x)(11-x)=112 \) を解けば，\( x \) の値を求めることができるので，
選んだ２つの数がわかるよ。
（１） 会話Ⅱの \( \boxed{ a } \) と \( \boxed{ b } \) にあてはまる数を，それぞれ求めなさい。
（２） かずこさんは，会話Ⅱの下線部のまなぶさんの考えをもとに，次のような方法を考えた。
次のかずこさんの考えの \( \boxed{ c } \) と \( \boxed{ d } \) にあてはまるものとして，最も適切なものを，あとのア～カからそれぞれひとつ選び,記号で答えなさい。
選んだ２つの数の和を \( A \)，積を \( B \) とする。\( x \) を自然数とすると，
２つの数は \( \dfrac{A}{2}+x，\dfrac{A}{2}-x \) と表される。
このとき，\( x \) を \( A \) と \( B \) の式で表すと，
\( x=\sqrt{ \boxed{ c } \; - \; \boxed{ d } } \)
となる。
ア \( A \) イ \( B \) ウ \( \dfrac{A}{2} \) エ \( \dfrac{B}{2} \) オ \( \left( \dfrac{A}{2} \right)^2 \) カ \( \left( \dfrac{B}{2} \right)^2 \)
問３ 和が \( 90 \)，積が \( 1961 \) となる２つの自然数を求めなさい。
大問４
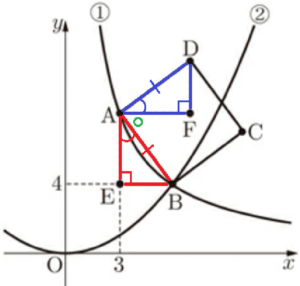
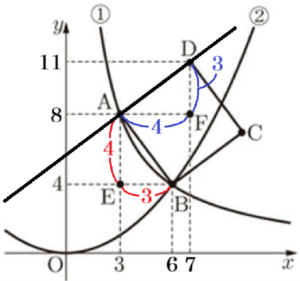
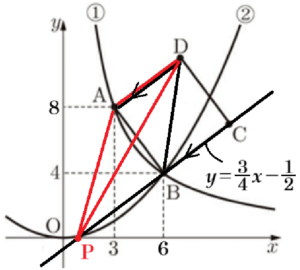
右の図において，曲線➀，放物線➁は，それぞれ関数 \( y=\dfrac{24}{x} \; (x>0) \)，関数 \( y=ax^2 \) のグラフであり，曲線➀上の点 \( A \) の \( x \) 座標は \( 3 \)，曲線➀と放物線➁の交点 \( B \) の \( y \) 座標は \( 4 \) である。また，四角形 \( ABCD \) は，線分 \( AB \) を一辺とする正方形である。さらに，点 \( E \) の座標は \( (3，4) \) であり，点 \( F \) を，点 \( A \) を通り \( x \) 軸に平行な直線と点 \( D \) を通り \( y \) 軸に平行な直線の交点とする。
このとき，あとの各問いに答えなさい。
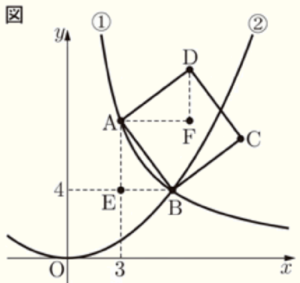
問１ 点 \( A \) の \( y \) 座標を求めなさい。
問２ \( a \) の値を求めなさい。
問３ \( △AEB≡△AFD \) であることを，次のように証明した。
このとき，あとの（１），（２）に答えなさい。
証明
\( △AEB \) と \( △AFD \) で，
正方形 \( ABCD \) の一辺の長さなので，
\( AB=AD \) ･･･ ➀
仮定より，\( AE，DF \) は \( y \) 軸に平行で，\( EB，AF \) は \( x \) 軸に平行なので,
\( \boxed{ a } \; = \; \boxed{ b } \; =90° \) ･･･ ➁
同様に，\( ∠FAE=90° \) ･･･ ➂
また，正方形 \( ABCD \) の１つの内角なので，
\( ∠BAD=90° \) ･･･ ➃
➂，➃から，\( ∠FAE=∠BAD \)
ここで， \( ∠BAE=∠FAE- \; \boxed{ c } \)
\( ∠DAF=∠BAD- \; \boxed{ d } \)
よって， \( ∠BAE=∠DAF \) ･･･ ➄
➀，➁，➄から，\( \boxed{ e } \) がそれぞれ等しいので,
\( △AEB≡△AFD \)
（１） 証明の \( \boxed{ a } \) ～ \( \boxed{ d } \) にあてはまる最も適切なものを，次のア～カから選び，それぞれ記号で答えなさい。
なお，同じ記号を何度使用してもよい。
ア \( ∠AFD \) イ \( ∠DAE \) ウ \( ∠FAB \)
エ \( ∠BAE \) オ \( ∠AEB \) カ \( ∠ABC \)
\( \boxed{ a } \) ･･･ オ \( ∠AEB \)
\( \boxed{ b } \) ･･･ ア \( ∠AFD \)
\( \boxed{ c } \) ･･･ ウ \( ∠FAB \)
\( \boxed{ d } \) ･･･ ウ \( ∠FAB \)
（２） 証明の \( \boxed{ c } \) にあてはまる最も適切な語句を入れて，証明を完成させなさい。
問４ ２点 \( A，D \) を通る直線の式を求めなさい。
\( △AEB≡△AFD \) であることから，
対応する辺の長さは等しいので，
\( AF=AE=4，DF=BE=3 \)
です。
ここから，点 \( D \) の座標は \( D(7，11) \) です。
求める直線の式を \( y=ax+b \) とすると，
傾き \( a \) は \( \dfrac{3}{4} \) であり，
\( y=\dfrac{3}{4}x+b \) に \( x=3，y=8 \) を代入すると，
\( 8=\dfrac{3}{4} \times 3+b \)
\( b=\dfrac{23}{4} \)
よって，求める直線の式は \( y=\dfrac{3}{4}x+\dfrac{23}{4} \) になります。
問５ \( △ADB=△ADP \) となるように \( x \) 軸上に点 \( P(t，0) \) をとる。このとき，\( t \) の値を求めなさい。
ただし，\( t>0 \) とする。
等積変形の考え方から，点 \( P \) が 直線 \( BC \) と \( x \) 軸との交点であるとき，
\( △ADB=△ADP \) となります。
点 \( B(6，4) \) は直線 \( BC \) 上の点なので，
直線 \( BC \) の式を \( y=\dfrac{3}{4}x+c \) とし，
\( x=6，y=4 \) を代入すると，
\( 4=\dfrac{3}{4} \times 6+c \)
\( c=-\dfrac{1}{2} \)
であり，直線 \( BC \) の式は \( y=\dfrac{3}{4}x-\dfrac{1}{2} \) です。
求める点 \( P(t，0) \) も，直線 \( BC \) 上の点なので，
\( y=\dfrac{3}{4}x-\dfrac{1}{2} \) に \( x=t，y=0 \) を代入すると，
\( 0=\dfrac{3}{4}t-\dfrac{1}{2} \)
\( 0=3t-2 \)
\( t=\dfrac{2}{3} \)
大問５
次の会話は，つむぎさんが身の回りにある図形について，先生と話し合ったものである。
このとき，あとの各問いに答えなさい。
会話
先 生：下の図Ⅰのように図形を２本の平行線ではさみ込んだとき，これら２本の平行線の間隔の
ことを「さしわたし幅」といいます。
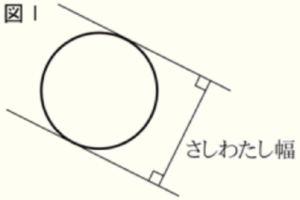
つむぎさん：ノギスという工具があれば，いろいろな図形の「さしわたし幅」を測ることができますね。
先 生：そうですね。例えば，円は「さしわたし幅」が一定の図形になります。正三角形はどう
でしょうか。
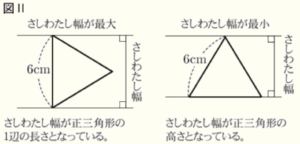
つむぎさん：正三角形は,「さしわたし幅」が最大になるときと最小になるときで幅が異なるので，
「さしわたし幅」が一定ではないことがわかります。
先 生：そうですね。この「さしわたし幅」が一定である性質を利用して，お掃除ロボットや硬貨が
作られています。「さしわたし幅」が一定である円以外の図形では,「ルーローの三角形」が
よく知られています。
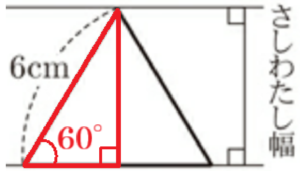
問１ 次の図Ⅱは，正三角形のさしわたし幅が最大になるときと，最小になるときを表している。正三角形の１辺の長さを \( 6 \; cm \) として，さしわたし幅が最小になるときのさしわたし幅を求めなさい。
もとめるさしわたし幅は，
１辺 \( 6 \; cm \) の正三角形の高さと等しいので，
求めるさしわたし幅を \( x \; cm \) とすると，
\( x=6 \times \dfrac{\sqrt{3}}{2}=3\sqrt{3} \; (cm) \)
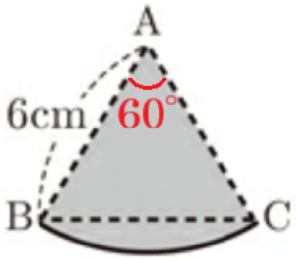
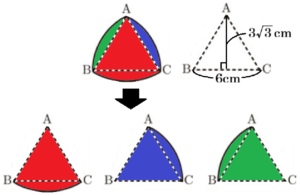
問２ 次の図Ⅲは，手順➀～➂にしたがって，１辺の長さが \( 6 \; cm \) の正三角形 \( ABC \) から「ルーローの三角形」を作ったものである。
このとき，次の（１），（２）に答えなさい。
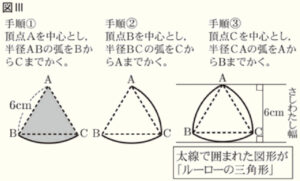
（１） 図Ⅲの手順➀によってできた色の付いた部分の図形は，おうぎ形となる。
このとき，おうぎ形の面積を求めなさい。
\( △ABC \) は正三角形であることから，
このおうぎ形は，半径 \( 6 \; cm \)，中心角 \( 60° \) の
おうぎ形になっています。
よって，このおうぎ形の面積は，
\( \pi{} \times 6^2 \times \dfrac{60°}{360°}=6\pi{} \; (cm^2) \)
（２） 図Ⅲの手順➀～➂で完成した「ルーローの三角形」の面積を求めなさい。
半径 \( 6 \; cm \)，中心角 \( 60° \) のおうぎ形３個分から１辺 \( 6 \; cm \) の正三角形 \( ABC \) ２個分を引いたもの
と考えることができます。
【おうぎ形の面積】
（１）より，\( 6\pi{} \; cm^2 \)
【正三角形 \( ABC \) の面積】
\( 6 \times 3\sqrt{3} \times \dfrac{1}{2}=9\sqrt{3} \; (cm^2) \)
なので，「ルーローの三角形」の面積は，
\( 6\pi{} \times 3-9\sqrt{3} \times 2=18\pi{}-18\sqrt{3} \; (cm^2) \)
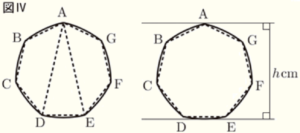
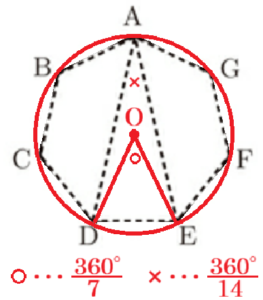
問３ 次の図Ⅳは，正七角形をもとにして作られた「ルーローの七角形」(頂点 \( A \) を中心に，対角線 \( AD \) の長さを半径とする弧 \( DE \) をかき，他の頂点についても同様に作図する)である。さしわたし幅が \( h \; cm \) であるとき，この「ルーローの七角形」の周の長さを求めなさい。
右の図のように正七角形 \( ABCDEFG \) と接する
円を書き，その円の中心を \( O \) とすると，
\( ∠DOE \) は，弧 \( DE \) に対する中心角なので，
\( ∠DOE=\dfrac{360°}{7} \)
\( ∠DAE \) は，弧 \( DE \) に対する円周角なので，
\( ∠DAE=\dfrac{360°}{14} \)
になっています。
このとき，おうぎ形 \( ADE \) は，
半径 \( h \; cm \) ，中心角 \( \dfrac{360°}{14} \) のおうぎ形なので，
弧 \( DE \) の長さは，
\( 2\pi{} \times h \times \dfrac{\dfrac{360°}{14}}{360°}=\dfrac{\pi{}h}{7} \; (cm) \)
「ルーローの七角形」の周の長さは，弧 \( DE \) の７倍なので，周の長さは，
\( \dfrac{\pi{}h}{7} \times 7=\pi{}h \; (cm) \)
