大問1
次の問いに答えなさい。
(1) \( 9+2×(-3) \) を計算しなさい。
【解説】
\( =9+(-6) \)
\( =3 \)
(2) \( 3x^2y \times 4y^2 \div 6xy \) を計算しなさい。
【解説】
\( =\dfrac{3x^2y \times 4y^2}{6xy} \)
\( =2xy^2 \)
(3) \( \dfrac{9}{ \sqrt{3}}- \sqrt{48} \) を計算しなさい。
【解説】
\( =\dfrac{9 \times \sqrt{3}}{ \sqrt{3} \times \sqrt{3}}- 4\sqrt{3} \)
\( =3\sqrt{3}- 4\sqrt{3} \)
\( =-\sqrt{3} \)
(4) \( 3(3a+b)-2(4a-3b) \) を計算しなさい。
【解説】
\( =9a+3b-8a+6b \)
\( =a+9b \)
(5) 連立方程式 \( \left\{
\begin{array}{}
2x+5y=-2 \\
3x-2y=16
\end{array}
\right. \) を解きなさい。
【解説】
\( 2x+5y=-2 \) ・・・ ➀
\( 3x-2y=16 \) ・・・ ➁
➀\( \times 3 \)
\( 6x+15y=-6 \) ・・・ ➀’
➁\( \times 2 \)
\( 6x-4y=32 \) ・・・ ➁’
➀’\(-\)➁’
\( 19y=-38 \)
\( y=-2 \)
➀に代入
\( 2x-10=-2 \)
\( 2x=8 \)
\( x=4 \)
(6) 2次方程式 \( (x-2)^2=25 \) を解きなさい。
【解説】
\( (x-2)^2=25 \)
\( x-2=±5 \)
\( x=7,-3 \)
(7) a 個のチョコレートを1人に8個ずつ b 人に配ると5個あまった。これらの数量の関係を等式で表しなさい。
【解説】
チョコレートを1人に8個ずつ \( b \) 人に配るために必要な個数 → \( 8b \)
よって, \( a=8b+5 \)
(8) 2つのさいころA. Bを同時に投げるとき,出た目の 大きい数から小さい数をひいた差が3となる確率を求めなさい。
ただし,それぞれのさいころの1から6までのどの目が出ることも同様に確からしいものとし,出た目の数が同じときの差は0とする。
【解説】
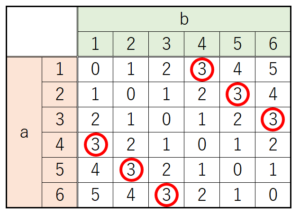
a,b それぞれの値に対して差がいくつになるかを表に書いて,
差が3となるマスに○をつけます。
すべての場合の数が36マス,○がついたマスは6マスなので,
求める確率は,\( \dfrac{6}{36}=\dfrac{1}{6} \)
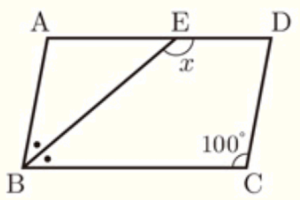
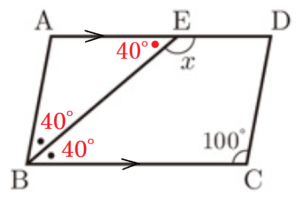
(9) 右の図のような平行四辺形 \( ABCD \) があり,\( BE \) は \( ∠ABC \) の二等分線である。\( ∠x \) の大きさを求めなさい。
【解説】
平行四辺形のとなりあう角の和は180°なので,\( ∠ABC=80° \)
\( BE \) は \( ∠ABC \) の二等分線なので,\( ∠EBC=40° \)
平行四辺形の向かい合う辺は平行なので,錯角が等しく,
\( ∠AEB=∠EBC=40° \)
よって,\( ∠x=180°-∠EBC=140° \)
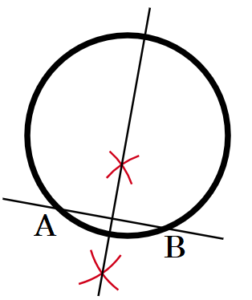
(10) 右の図形は円である。この図形の対称の軸を1本,作図によって求めなさい。
ただし,作図に用いた線は残しておくこと。
【解答&解説】
対称の軸は折り返したときにぴったり重なるような折り目の線と同じなので,
円の場合,中心を通る直線になります。
円の中心を通る直線が弦と垂直に交わるとき,その直線は弦を二等分します。
つまり,弦に対しての垂直二等分線が対称の軸になります。
手順1 円と交わるように直線をひく(交点を点 \( A,B \) とする )
手順2 点 \( A,B \) を中心に同じ半径で弧を描く
手順3 手順2の弧の交点を結ぶ直線を描く
大問2
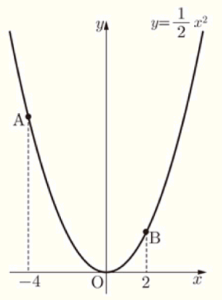
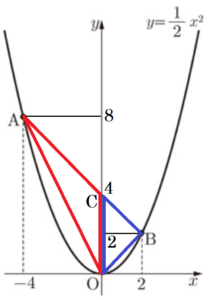
右の図のように,関数 \( y=1/2x^2 \) のグラフ上に2点 \( A,B \) があり,\( x \) 座標はそれぞれ \( -4,2 \) である。このとき,次の問いに答えなさい。
(1) 関数 \( y=1/2x^2 \) について,\( x \) の変域が \( -1≦x≦2 \) のときの \( y \) の変域を求めなさい。
【解説】
関数 \( y=ax^2 \) ( \(a>0\) ) において,
\( x \) の変域が \( 0 \) を含んでいるとき,\( y \) の最小値は \( 0 \) になります。
また,\( y \) の値は,\( x \) の絶対値が大きいほど大きくなるので,
\( x \) の変域が \( -1≦x≦2 \) のとき,\( y \) が最大値をとるのは,\( x=2 \) のとき。
\( x=2 \) のときの \( y \) の値は,
\( y=\dfrac{1}{2}×2^2=2 \)
よって,\( y \) の変域は,\( 0≦y≦2 \)
(2) \( △OAB \) の面積を求めなさい。
【解説】
\( AB \) と \( y \) 軸の交点を点 \( C \) とし,
\( △OAB=△OAC+△OBC \) として考えます。
\( A(-4,8),B(2,2) \) なので,直線 \( AB \) の式は
\( y=-x+4 \) になります。
\( △OAC \) と \( △OBC \) の底辺を \( OC \) とすると,
高さは,\( 4 \) と \( 2 \) になるので,
\( △OAB=△OAC+△OBC \)
\( =4 \times 4 \times \dfrac{1}{2}+4 \times 2 \times \dfrac{1}{2} \)
\( =12 \)
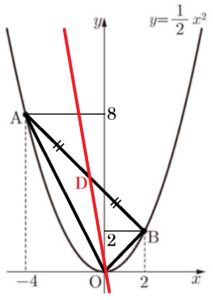
(3) 点 \( O \) を通り,\( △OAB \) の面積を2等分する直線の式を求めなさい。
【解説】
求める直線と直線 \( AB \) の交点を点 \( D \) とすると,
\( △OAD \) と \( △OBD \) は,高さが共通なので,
面積が等しくなる時,底辺の長さも等しくなります。
つまり,点 \( D \) は辺 \( AB \) の中点になります。
\( A(-4,8),B(2,2) \) なので, \( AB \) の中点の
\( x \) 座標は,\( \dfrac{-4+2}{2}=-1 \)
\( y \) 座標は,\( \dfrac{8+2}{2}=5 \)
よって,求める直線は原点と \( D(-1,5) \) を通るので,
この直線の式は, \( y=-5x \)
大問3
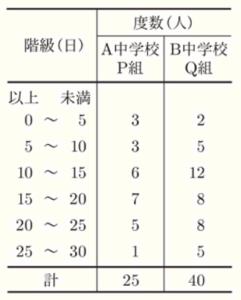
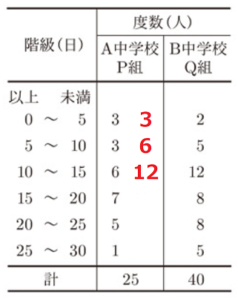
A中学校とB中学校では,英語で日記を書く活動を行っている。A中学校P組の生徒数は25人で,B中学校Q組の生徒数は40人である。右の表は,P組,Q組の生徒全員について,ある月に英語で日記を書いた日数を度数分布表に整理したものである。
このとき,次の問いに答えなさい。
(1) P組について,0日以上5日未満の階級の相対度数を求めなさい。
【解説】
[相対度数]=[度数] \( \div \) [データの総数] なので,
[相対度数] \( =3 \div 25 \)
\( =0.12 \)
(2) P組について,中央値がふくまれる階級を答えなさい。
【解説】
P組の生徒数は25人なので,中央値になるのは,
少ない方から13番目の値になります。
P組の度数分布表において,累積度数を考えると,
10日 以上15日未満の階級で12なので,
中央値(13番目の値)がふくまれる階級は,
「15日 以上20日未満」になります。
(3) 度数分布表からわかることとして,必ず正しいといえるものを次のア~オからすべて選び,記号で答えなさい。
ア Q組では,英語で日記を15日以上書いた生徒が20人以上いる。
イ P組とQ組では,英語で日記を書いた日数の最頻値は等しい。
ウ P組とQ組では,英語で日記を書いた日数が20日 以上25日未満である生徒の割合は等しい。
エ 英語で日記を書いた日数の最大値は,Q組の方がP組より大きい。
オ 5日以上10日未満の階級の累積相対度数は,P組の方がQ組より大きい。
【解説】
ア Q組の15日以上書いた生徒は \( 8+8+5=21 \) 人。
イ 最頻値は度数が最も大きい階級のの階級値のことなので,
P組が17.5日,Q組が12.5日
ウ 生徒の割合というのは,相対度数のことなので,
P組\( =5 \div 25=0.25 \),Q組\( =8 \div 40=0.25 \)
エ 最大値を含む階級が同じなので,この度数分布表では,どちらが大きいかは判断できません。
オ [累積相対度数]=[累積度数] \( \div \) [データの総数] なので,
P組\( =6 \div 25=0.24 \),Q組\( =7 \div 40=0.175 \)
大問4
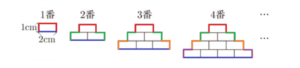
次の図のように,縦の長さが \( 1 \: cm \),横の長さが \( 2 \: cm \) の長方形のタイルを1枚置き,1番の図形とする。1番の図形の下に,タイル2枚を半分ずらしてすきまなく並べてできた図形を2番の図形,2番の図形の下に,タイル3枚を半分ずらしてすきまなく並べてできた図形を3番の図形とする。以下,この作業を繰り返してできた図形を,4番の図形,5番の図形,・・・ とする。

ひかるさんとゆうきさんは,1番,2番,3番 ・・・ と,図形の番号が変わるときの,タイルの枚数や周の長さについて話している。ただし,図形の周の長さとは,太線 ( ー ) の長さである。2人の [会話1],[会話Ⅱ] を読んで,それぞれについて,あとの問いに答えなさい。
[会話1]
ひかる 図形のタイルの枚数を調べると,1番の図形は1枚,2番の図形は3枚になり,
6番の図形は ア 枚になるね。
ゆうき 私は図形の周の長さを調べてみたよ。1番の図形は \( 6 \: cm \),
2番の図形は \( 12 \: cm \) になり,\( n \) 番の図形は \( n \) を使って表すと,
イ \( cm \) となるね。
(1) [会話Ⅰ] の ア にあてはまる数を求めなさい。
【解説】
6番の図形の枚数は,\( 1+2+3+4+5+6=21 \) 枚
(2) [会話Ⅰ] の イ にあてはまる式を,n を使って表しなさい。
【解説】
下の図で,赤の部分の \( 4 \: cm \) はすべての図形で共通です。
\( n \) 番目の図形において,青の底の部分の長さは \( 2 \: cm \) が \( n \) 枚分で,\( 2n \: cm \)
左右の折れ曲がった部分(緑・オレンジ・紫)の長さは,L字(?)型が \( n-1 \) 枚分で,\( 2(n-1) \: cm \)
なので,周の長さは,\( 4+2n+2(n-1) \times 2=6n \: cm \)
[会話Ⅱ]
ひかる 図形のタイルの枚数について,表にまとめてみたよ。

ゆうき 私は図形の周の長さについて,表にまとめてみたよ。

ひかる 2つの表をくらべると, ウ 番の図形では,タイルの枚数が エ 枚で,
周の長さが エ \( cm \) となって,数値が等しくなっているよ。
ゆうき そうだね。単位はちがっても,数値が等しくなるのはおもしろいね。
(3) [会話Ⅱ] の ウ , エ にあてはまる数をそれぞれ求めなさい。
【解答】
ウ ・・・ \( 11 \) エ ・・・ \( 66 \)
【解説】
それぞれの図形の上下を入れ替えて横に並べると,
\( n \) 番目の図形は,\( n+1 \) 枚が \( n \) 段積み重なった図形になります。
このとき,\( n \) 番目の図形のタイルの枚数は,\( \dfrac{n(n+1)}{2} \) 枚と表すことができます。
 ウ
ウ
よって,タイルの枚数と周の長さが等しくなるのは,
\( \dfrac{n(n+1)}{2}=6n \)
\( n(n+1)=12n \)
\( n^2-11n=0 \)
\( n(n-11)=0 \)
\( n=11 \) (\( n>0 \) より)
エ
\( n=11 \) のとき,\( 6n=66 \)
大問5
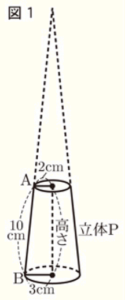
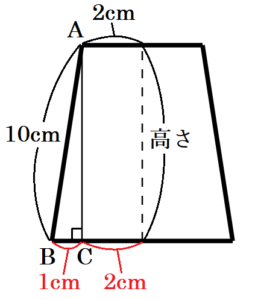
右の図1のように,円すいを底面に平行な平面で切ってできる2つの立体のうち,底面をふくむ 立体を \( P \) とする。円すいの底面の半径は \( 3 \: cm \),切り口の円の半径は \( 2 \: cm \) である。また,線分 \( AB \) は円すいの母線の一部分であり,その長さは \( 10 \: cm \) である。
このとき,次の問いに答えなさい。ただし,円周率は \( \pi{} \) とする。
(1) 立体 \( P \) の高さを求めなさい。ただし,立体 \( P \) の高さとは,円すいの底面の円の中心と切り口の円の中心を結んだ線分の長さである。
【解答】
\( 3 \sqrt{11} \: cm \)
【解説】
右図のように点 \( A \) から底面に垂線をひき,
交点を \( C \) とすると,\( AC \) の長さは高さと等しいので,
\( △ABC \) において,三平方の定理より,
\( AC^2=AB^2-BC^2 \)
\( =10^2-1^2 \)
\( =99 \)
\( AC=3 \sqrt{11} \; (cm) \) (\( AC>0 \)より)
(2) 立体 \( P \) の体積を求めなさい。
【解答】
\( 19\sqrt{11}\pi{} \: cm^3 \)
【解説】
切る前の円すいを 円すい \( Q \) ,切りとった円すいを円すい \( R \) とすると,\( P=Q-R \) となります。
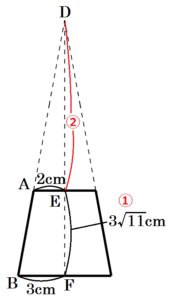
右の図のように点 \( D,E,F \) をとると,
\( △DAE \)∽\( △DBF \) で相似比は \( 2:3 \) なので,
\( DE:DF=2:3 \) より,\( DE:EF=2:1 \)
\( DE:3 \sqrt{11}=2:1 \)
\( DE=2 \times 3\sqrt{11} \)
\( =6\sqrt{11} \; (cm) \)
よって,
\( Q=\pi{} \times 3^2 \times (6\sqrt{11}+3\sqrt{11}) \times \dfrac{1}{3} \)
\( =27\sqrt{11}\pi{} \; (cm^3) \)
\( R=\pi{} \times 2^2 \times 6\sqrt{11} \times \dfrac{1}{3} \)
\( =8\sqrt{11}\pi{} \; (cm^3) \)
\( P=Q-R=19\sqrt{11}\pi{} \; (cm^3) \)
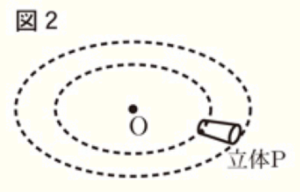
(3) 右の図2のように,立体 \( P \) をたおして平面上に置き,すべらないように転がしたところ,立体 \( P \) は,点 \( O \) を中心とする2つの円の間を何回か回転しながら1周して,もとの位置にもどった。
このとき,立体 \( P \) は何回の回転をしたか求めなさい。
【解説】
切り取る前の円すい \( Q \) で考えると,点 \( O \) と点 \( D \) が一致します。
(2)より,\( △DAE \)∽\( △DBF \),\( DE:EF=2:1 \) なので,
\( AB=10 \: cm \) より,\( DA=20 \: cm,DB=30 \: cm \)
よって,図2の外側の円は,半径 \( 30 \: cm \) の円なので,
立体 \( P \) の回転数= \( \dfrac{半径 30 \: cm の円周}{立体 P の底面の周の長さ} \)
\( =\dfrac{2\pi{} \times 30}{2\pi{} \times 3}=10 \) (回)
大問6
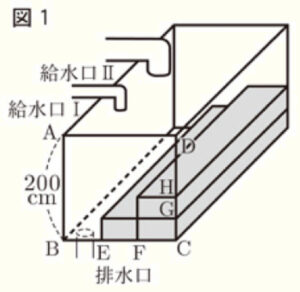
右の図1のように,高さが \( 200 \: cm \) の直方体の水そうの中に,3つの同じ直方体が,合同な面どうしが重なるように階段状に並んでいる。3つの直方体および直方体と水そうの面との間にすきまはない。この水そうは水平に置かれており,給水口Ⅰと給水口Ⅱ,排水口がついている。
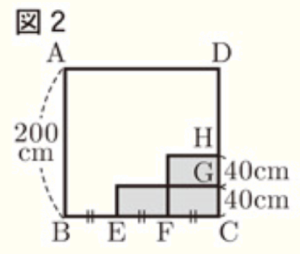
図2はこの水そうを面 \( ABCD \) 側から見た図である。点 \( E,F \) は,辺 \( BC \) 上にある直方体の頂点であり,\( BE=EF=FC \) である。また,点 \( G,H \) は,辺 \( CD \) 上にある直方体の頂点であり,\( CG=GH=40 \: cm \) である。
この水そうには水は入っておらず、給水口Ⅰと給水口Ⅱ,排水口は閉じられている。この状態から、次のア〜ウの操作を順に行った。
ア 給水口Ⅰのみを開き,給水する。
イ 水面の高さが \( 80 \: cm \) になったときに,給水口Ⅰを開いたまま給水口Ⅱを開き,給水する。
ウ 水面の高さが \( 200 \: cm \) になったところで,給水口Ⅰと給水口Ⅱを同時に閉じる。
ただし、水面の高さとは、水そうの底面から水面まで の高さとする。
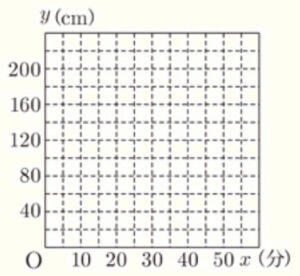
給水口Ⅰを開いてから \( x \) 分後の水面の高さを \( y \: cm \) とするとき,\( x \) と \( y \) の関係は,右の表のようになった。
このとき,次の問いに答えなさい。ただし,給水口Ⅰと給水口Ⅱ,排水口からはそれぞれ一定の割合で水が流れるものとする。
(1) \( x=1 \) のとき,\( y \) の値を求めなさい。
【解答&解説】
\( y \) の値は,\( x \) の値の4倍になっているので,\( y=1 \times 4=4 \)
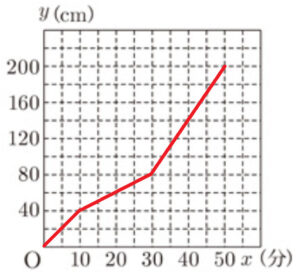
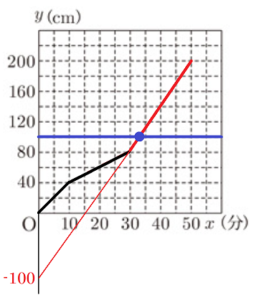
(2) 給水口Ⅰを開いてから,給水口Ⅰと給水口Ⅱを同時に閉じるまでの \( x \) と \( y \) の関係を表すグラフをかきなさい。
【解答&解説】
\( 0≦y≦40,40≦y≦80,80≦y≦200 \) でそれぞれ底面積が変わるので,別々に考えます。
● \( 0≦y≦40 \)
表より,\( x=5 \) のとき,\( y=20 \) なので,
\( y=40 \) になるのは,\( x=10 \) のとき
● \( 40≦y≦80 \)
\( BF=2BE \) より,底面積は \( 0≦y≦40 \) の場所の2倍。
給水される水の量は同じで底面積が2倍になっているので,
水面の高さが \( 40 \: cm \) 高くなるのにかかる時間も2倍になります。
よって,\( y=80 \) になるのは,\( x=30 \) のとき
● \( 80≦y≦200 \)
表より,\( y=200 \) になるのは,\( x=50 \) のとき
原点とこれらの点を直線で結ぶと,右のようになります。
(3) 水面の高さが \( 100 \: cm \) になるのは,給水口Ⅰを開いてから何分何秒後か求めなさい。
【解説】
(2) のグラフより,水面の高さが \( 100 \: cm \) になるのは,
● のところです。
グラフの赤の直線は,\( (30,80),(50,200) \) を通っているので,
傾き \( =\dfrac{200-80}{50-30}=6 \)
この直線の式を \( y=6x+b \) とし,
\( x=50,y=200 \) を代入すると,
\( 200=6 \times 50+b \)
\( b=-100 \)
なので,この直線の式は \( y=6x-100 \)
\( y=100 \) を代入すると,
\( 100=6x-100 \)
\( x=\dfrac{100}{3} \)
よって,水面の高さが \( 100 \: cm \) になるのは,\( \dfrac{100}{3}=33\dfrac{1}{3} \) 分後。
\( \dfrac{1}{3} \) 分を秒になおすと,
60秒の \( \dfrac{1}{3} \) なので,\( 60 \times \dfrac{1}{3}=20 \) 秒後。
(4) 水面の高さが \( 200 \: cm \) の状態から,給水口Iと給水口Ⅱを閉じたまま排水口を開いたところ,60分後にすべて排水された。排水口を開いてから48分後の水面の高さを求めなさい。
【解説】
すべて排水される12分前の水面の高さを求めることにします。
水面の高さが \( 40 \: cm \) から \( 0 \: cm \) まで排水されるのにかかる時間を \( t \) 分とすると,
\( 80 \: cm \) から \( 40 \: cm \) までは,高さが同じで底面積が2倍なので,\( 2t \) 分かかります。
\( 200 \: cm \) から \( 80 \: cm \) までは,高さが3倍で底面積が3倍なので,\( 9t \) 分かかります。
すべて排水するのにかかる時間は \( t+2t+9t=12t \) 分なので,\( 12t=60 \) より,\( t=5 \)
よって,すべて排水される5分前の水面の高さが \( 40 \: cm \) ということです。
\( 0≦y≦40 \) の範囲では,毎分 \( 8 \: cm \) 水面の高さが下がっているので,
\( 40≦y≦80 \) の範囲では,毎分 \( 4 \: cm \) 水面の高さが下がります。
つまり,7分間では \( 28 \: cm \) 水面の高さが下がるので,
すべて排水される12分前の水面の高さは,\( 40+28=68 \: cm \)
大問7
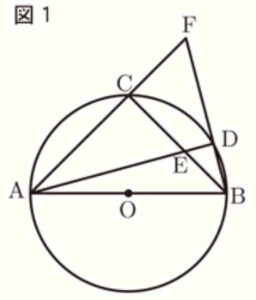
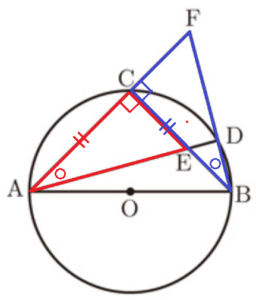
右の図1のように,線分 \( AB \) を直径とした円 \( O \) がある。円 \( O \) の周上に点 \( C \) があり,\( AC=BC \) である。また,点 \( A \) を含まない弧 \( BC \) 上に点 \( D \) をとり,線分 \( AD \) と線分 \( BC \) の交点を \( E \),直線 \( AC \) と直線 \( BD \) の交点を \( F \) とする。このとき,次の問いに答えなさい。ただし,点 \( D \) は \( B,C \) と一致しないものとし,円周率は \( \pi{} \) とする。
(1) \( △ACE≡△BCF \) を証明しなさい。
【解答&解説】
\( △ACE \) と \( △BCF \) において,
仮定より,\( AC=BC \) ・・・ ①
弧 \( CD \) の円周角なので,\( ∠CAE=∠CBF \) ・・・ ➁
直径 \( AB \) の円周角なので,\( ∠ACE=90° \) ・・・ ➂
点 \( C \) は,直線 \( AF \) 上の点なので,
\( ∠BCF=180°-∠ACE=180°-90°=90° \) ・・・ ④
➂④より,\( ∠ACE=∠BCF=90° \) ・・・ ➄
①②➄より,1組の辺の長さとその両端の角の大きさが等しいので,
\( △ACE≡△BCF \)
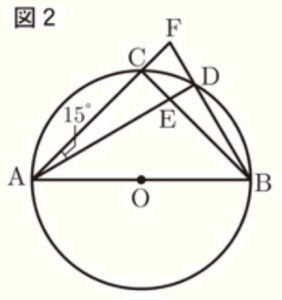
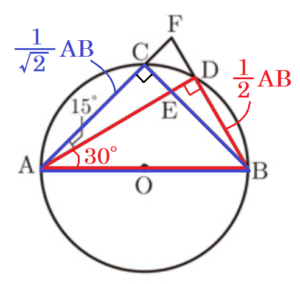
(2) 点 \( D \) を,図2のように \( ∠CAD=15° \) となるようにとったとき,\( △ACE \) と \( △BDE \) の面積比を求めなさい。
【解説】
\( ∠CAE=∠DBE,∠CEA=∠DEB \) より,
\( △ACE \) ∽ \( △BDE \)
\( △ABC \) は直角二等辺三角形なので,\( AC=\dfrac{1}{ \sqrt{2}}AB \)
\( ∠BAD=∠BAC-∠CAE=30°,∠ADB=90° \) より,
\( △ABD \) は \(30°,60°,90\) の直角三角形なので,
\( BD=\dfrac{1}{2}AB \)
よって, \( △ACE \) と \( △BDE \) の相似比は,
\( AC:BD=\dfrac{1}{ \sqrt{2}}AB:\dfrac{1}{2}AB=\sqrt{2}:1 \)
相似な三角形の面積比は,相似比の2乗の比と等しいので,
\( △ACE:△BDE=(\sqrt{2})^2:1^2=2:1 \)
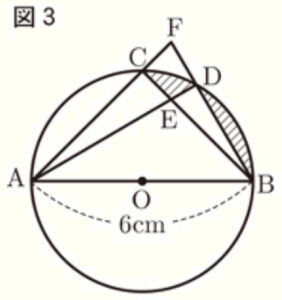
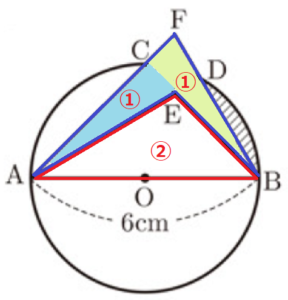
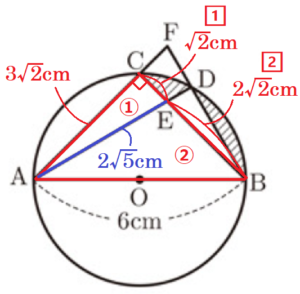
(3) 点 \( D \) を,図3のように \( △ABF \) の面積が \( △ABE \) の面積の2倍となるようにとる。
\( AB=6cm \) のとき,図の斜線部分の面積を求めなさい。
【解答】
\( \dfrac{9}{4}\pi{}-\dfrac{57}{10} \: cm^2 \)
【解説】
斜線部の面積\(=\)おうぎ形\( OBC-(△OBC+△BDE) \) として求めます。
\( △ABF \) の面積は \( △ABE \) の面積の2倍なので,
\( △ABE= \)四角形 \( AEBF \)
(1) より,\( △ACE≡△BCF \) なので,
\( △ACE=\dfrac{1}{2} \) 四角形 \( AEBF =\dfrac{1}{2}△ABE \)
よって,\( △ACE:△ABE=1:2 \)
\( △ACE \) と \( △ABE \) は,高さ \( CA \) が共通なので,
\( CE:EB=△ACE:△ABE=1:2 \)
\( △ABC \) は直角二等辺三角形なので,\( AC=BC=\dfrac{1}{\sqrt{2}} \times 6=3\sqrt{2} \: (cm) \)
\( CE:EB=1:2 \) より,\( CE=\dfrac{1}{3}AB=\sqrt{2} \: cm \),\( EB=\dfrac{2}{3}AB=2\sqrt{2} \: (cm) \)
\( △ACE \) において,三平方の定理より,
\( AE^2=(3\sqrt{2})^2+(\sqrt{2})^2=20 \)
\( AE=2\sqrt{5} \: (cm) \)
(2) より,\( △ACE \) ∽ \( △BDE \) なので,
相似比は,\( AE:BE=2\sqrt{5}:2\sqrt{2}=\sqrt{5}:\sqrt{2} \),
面積比は,\( △ACE:△BDE=(\sqrt{5})^2:(\sqrt{2})^2=5:2 \)
\( △ABC=AB \times OC \times \dfrac{1}{2}=9 \: (cm^2) \) なので,
\( △ACE=\dfrac{1}{3}△ABC=3 \: (cm^2) \),
\( △BDE=\dfrac{2}{5}△ACE=\dfrac{6}{5} \: (cm^2) \)
おうぎ形\( OBC=\pi{} \times 3^2 \times \dfrac{1}{4}=\dfrac{9}{4}\pi{} \: (cm^2) \)
\( △OBC=\dfrac{1}{2}△ABC=\dfrac{9}{2} \: (cm^2) \)
以上より,
斜線部の面積\(=\)おうぎ形\( OBC -( △OBC+△BDE ) \)
\( =\dfrac{9}{4}\pi{}- \left( \dfrac{9}{2}+\dfrac{6}{5} \right) \)
\( =\dfrac{9}{4}\pi{}-\dfrac{57}{10} \: (cm^2) \)