大問1
(1) \( (-2) \times 4 \) を計算しなさい。
(2) \( (-3)^2+8 \) を計算しなさい。
【解説】
\( =9+8 \)
\( =17 \)
(3) \( 7x-(6x-1) \) を計算しなさい。
【解説】
\( =7x-6x+1 \)
\( =x+1 \)
(4) \( \dfrac{9a^3}{5b} \div \dfrac{3a^2}{2b^2} \) を求めなさい。
【解答】
\( \dfrac{6ab}{5} \)
【解説】
\( =\dfrac{9a^3}{5b} \times \dfrac{2b^2}{3a^2} \)
\( =\dfrac{9a^3 \times 2b^2}{5b \times 3a^2} \)
\( =\dfrac{3a \times 2b}{5} \)
\( =\dfrac{6ab}{5} \)
(5) \( \sqrt{12}-\sqrt{27} \) を計算しなさい。
【解説】
\( =2\sqrt{3}-3\sqrt{3} \)
\( =-\sqrt{3} \)
大問2
(1) \( y \) が \( x \) に反比例し,\( x=2 \) のとき \( y=6 \) である。\( x=4 \) のときの \( y \) の値を求めなさい。
【解説】
反比例の式は \( y=\dfrac{a}{x} \) (\( a \) は定数) と表すことができるので,
\( x=2,y=6 \) を代入すると,
\( 6=\dfrac{a}{2} \)
\( a=12 \)
よって,\( y=\dfrac{12}{x} \) に \( x=4 \) を代入すると,
\( y=\dfrac{12}{4}=3 \)
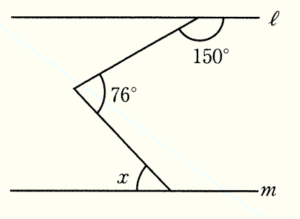
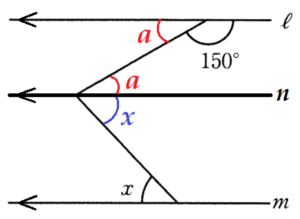
(2) 右の図で,\( ℓ//m \) のとき,\( ∠x \) の大きさを求めなさい。
【解説】
右の図のように \( ℓ//m//n \) となるような
直線 \( n \) をひくと,
\( ∠a+∠x=76° \) と表すことができます。
\( ∠a=180°-150°=30° \) なので,
\( ∠a+∠x=76° \)
\( 30°+∠x=76° \)
\( ∠x=46° \)
(3) 二次方程式 \( 2x^2+3x-1=0 \) を解きなさい。
【解答】
\( x=\dfrac{-3±\sqrt{17}}{4} \)
【解説】
この二次方程式を \( ax^2+bx+c=0 \) とすると,\( a=2,b=3,c=-1 \) なので,
解の公式より,
\( x=\dfrac{-3±\sqrt{3^2-4 \times 2 \times (-1)}}{2 \times 2} \)
\( =\dfrac{-3±\sqrt{17}}{4} \)
(4) ある池で \( 50 \) 匹の魚をつかまえ,その全部に印をつけて池に戻した。数日後,同じ池で \( 40 \) 匹の魚をつかまえたところ,印のついた魚が \( 11 \) 匹いた。この数日の間に,この池にいる魚の数と,印のついた魚の数に変化がないとするとき,この池にいる魚はおよそ何匹と推定されるか。
一の位を四捨五入した概数で答えなさい。
【解説】
池にいる魚全体の数:印のついた魚全体の数 \( = \) つかまえた魚の数:つかまえた魚のうち印のついた魚の数
となるので,
池にいる魚全体の数を \( P \) とすると,
\( P:50=40:11 \)
\( 11P=2000 \)
\( P=181.8・・・ \)
一の位を四捨五入すると,\( P=180 \)
大問3
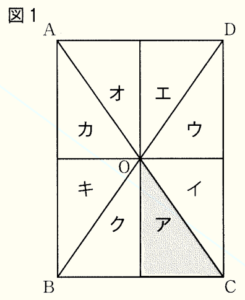
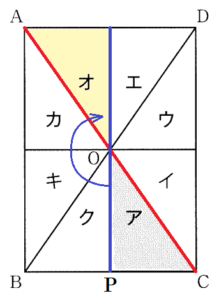
(1) 図1の長方形すると,\( ABCD \) において,図形ア~クは合同な直角三角形である。アを,点 \( O \) を中心として平面上で回転移動させたとき,アと重ねあわせることができる図形が図1中に1つある。その図形をイ~クから選び,記号で答えなさい。
【解説】
直角三角形 ア の3つの角のうち,\( ∠O \) は小さい方の鋭角に
なっています。
イ~クのうち,\( ∠O \) が小さい方の鋭角になっているのは,
エ,オ,ク の3つです。
点 \( O \) から辺 \( BC \) に垂線をひいた交点を点 \( P \) とするとき,
線分 \( PO \)(長辺)と線分 \( OC \)(斜辺)は
カタカナの「フ」の形になっています。
直角三角形 エ,オ,ク のうち,
長辺と斜辺の位置関係がカタカナの「フ」の形になっているのは
オ になります。
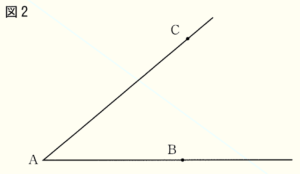
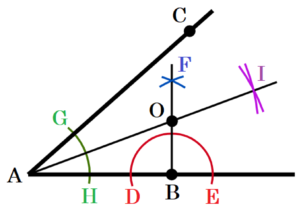
(2) 図2のように, 半直線 \( AB,AC \) がある。半直線 \( AB,AC \) のどちらにも接する円のうち,半直線 \( AB \) と点 \( B \) で接する円の中心 \( O \) を作図しなさい。ただし,作図に用いた線は消さないこと。
【解答】
手順1 点 \( B \) を中心に円弧を描く。
(半直線 \( AB \) との交点を点 \( D,E \) とします)
手順2 点 \( D,E \) を中心に円弧を描く。
(交点を点 \( F \) とします)
手順3 点 \( B,F \) を通る直線を描く。
手順4 点 \( A \) を中心に円弧を描く。
(半直線 \( AC,AB \) との交点を点 \( G,H \) とします)
手順5 点 \( G,H \) を中心に円弧を描く。
(交点を点 \( I \) とします)
手順6 点 \( A,I \) を通る直線を描く。
手順3と6の直線の交点が求める点 \( O \) になります。
【解説】
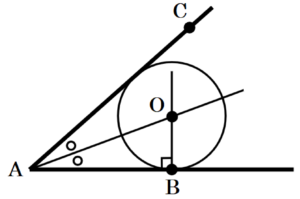
円と接線については,以下の性質があるので,
これを利用して点 \( O \) の位置を求めます。
・ 円の半径と接線は接点において垂直に交わる
・ 円 \( O \) の外部の点 \( A \) から2本の接線をひいたとき,直線 \( OA \) は \( ∠A \) の二等分線になる。(注)
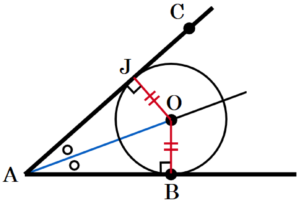
直線OAが∠Aの二等分線になる理由
接線 \( AC \) と円 \( O \) の接点を点 \( J \) とすると,
\( △OAB \) と \( △OAJ \) において,
線分 \( OA \) は共通 ・・・ ➀
円 \( O \) の半径なので,\( OB=OJ \) ・・・ ➁
円の半径と接線は接点において垂直に交わるので,
\( ∠OBA=∠OJA=90° \) ・・・ ③
➀➁③より,
直角三角形において,斜辺と他の1辺がそれぞれ等しいので,
\( △OAB≡△OAJ \)
対応する角は等しいので,
\( ∠OAB=∠OAJ \)
大問4
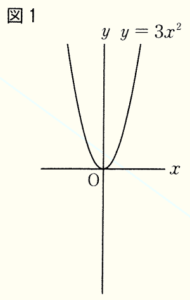
(1) 図1は,関数 \( y=3x^2 \) のグラフである。下のア~エは,図1と同じ座標軸を使って,\( y=ax^2 \) の形で表される関数のグラフをそれぞれ図1にかき加えた図であり,そのうちの1つが関数 \( y=-\dfrac{1}{3}x^2 \) のグラフをかき加えたものである。
関数 \( y=-\dfrac{1}{3}x^2 \) のグラフをかき加えた図として最も適切なものを,ア~エから選び,記号で答えなさい。
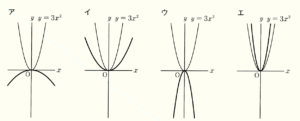
【解説】
\( y=-\dfrac{1}{3}x^2 \) は,\( y=ax^2 \) に \( a=-\dfrac{1}{3} \) を代入したものなので,
\( a=-\dfrac{1}{3}<0 \) より,かき加えたグラフは上に凸になります。
ここから,正しい図は
アまたは
ウになります。
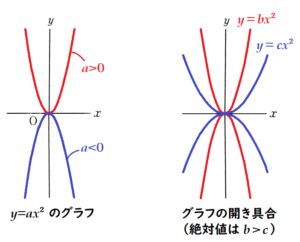
二次関数のグラフは,係数の絶対値が小さいほどグラフの開き具合が大きく(平らな形に)なります。
\( 3 \) と \( -\dfrac{1}{3} \) では,\( -\dfrac{1}{3} \) の方が絶対値が小さいので,
書き加えたグラフの方が,より平らな形になります。
ここから,正しい図はアになります。
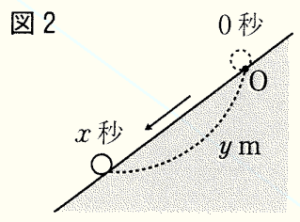
(2) 図2のような斜面で,点 \( O \) の位置からボールを転がす。
ボールが転がり始めてから \( x \) 秒間に転がる距離を \( y \; m \) とする
とき,\( x \) と \( y \) の間には,\( y=3x^2 \) の関係がある。
このとき,次の文章が正しくなるように ア , イ にあてはまる数を求めなさい。
ボールがこの斜面を転がり始めて \( 2 \) 秒後から \( 4 \) 秒後までの平均の速さは,毎秒 ア \( m \) である。また,ボールが転がり始めてから \( t \) 秒後までの平均の速さが毎秒 ア \( m \) であるとき,\( t= \) イ である。
【解答】
ア ・・・ \( 18 \)
イ ・・・ \( 6 \)
【解説】
ア
転がり始めて \( 2 \) 秒後までに転がる距離は,\( y=3 \times 2^2=12 \; (m) \)
転がり始めて \( 4 \) 秒後までに転がる距離は,\( y=3 \times 4^2=48 \; (m) \)
なので,\( 2 \) 秒後から \( 4 \) 秒後までの \( 2 \) 秒間に転がる距離は,\( 48-12=36 \; (m) \)
よって,平均の速さは,毎秒 \( \dfrac{36}{2}=18 \; (m) \)
イ
転がり始めて \( t \) 秒後までに転がる距離は,\( 3t^2 \; m \) と表すことができるので,
\( t \) 秒後までの平均の速さは,毎秒 \( \dfrac{3t^2}{t}=3t \; (m) \) (\( t>0 \) より)
よって,
\( 3t=18 \)
\( t=6 \)(秒後)
大問5
Rさんは,図1の展開図を組み立ててできる特殊なさいころを2個つくり,できたさいころを図2のように,それぞれさいころA,さいころBとした。
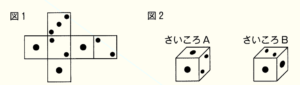
次の(1),(2)に答えなさい。ただし,さいころA,さいころBはどの面が出ることも同様に確からしいものとする。
(1) さいころAを1回投げるとき,1の目が出る確率を求めなさい。
【解説】
さいころは全部で6面あり,そのうち,1の目は3面あるので,
求める確率は,\( \dfrac{3}{6}=\dfrac{1}{2} \)
(2) さいころAとさいころBを同時に1回投げるとき,出る目の数の和について,Rさんは次のように予想した。
【Rさんの予想】
出る目の数の和は,2になる確率が最も高い。
Rさんの予想は正しいか,正しくないか。確率を求めるまでの過程を明らかにして説明しなさい。
【解答】
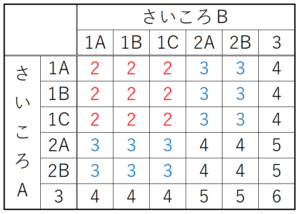
3つの1の面を「1A」,「1B」,「1C」,
2つの2の面を「2A」,「2B」として
2つのさいころの出た目の組み合わせとその和を
表にすると,右の表のようになる。
2つのさいころの出た目の組み合わせは36通り,
出た目の和が2になるのは9通りなので,
確率は \( \dfrac{9}{36}=\dfrac{1}{4} \)
出た目の和が3になるのは12通りなので,
確率は \( \dfrac{12}{36}=\dfrac{1}{3} \)
よって,出た目の和が3になる確率の方が高いので,
Rさんの予想は正しくない。
大問6
Sさんは授業でフェアトレードについて学習した。フェアトレードとは,発展途上国で生産された農作物や製品を適正な価格で購入することで,その国の人々の生活改善と自立をめざす貿易の仕組みである。
次の(1),(2)に答えなさい。
(1) コーヒー1杯の販売価格 \( 400 \) 円に対して,コーヒー豆の生産者の収入を \( a \) 円とする。このとき,このコーヒー1杯の販売価格に対する生産者の収入の割合は何%になるか。\( a \) を使った式で表しなさい。
【解答】
\( \dfrac{a}{4} \) %
【解説】
\( \dfrac{a}{400} \times 100=\dfrac{a}{4} \) %
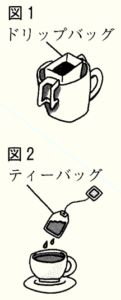
(2) Sさんたちは,地域の祭りでフェアトレードについての紹介をし,フェアトレード製品である図1のようなコーヒーのドリップバッグと,図2のような紅茶のティーバッグを売ることにした。
Sさんたちは,ドリップバッグとティーバッグを仕入れて,ドリップバッグ \( 3 \) 個を袋に入れた商品と,ティーバッグ \( 4 \) 個を袋に入れた商品の2種類の商品をつくる予定である。
それぞれの仕入れ価格は,ドリップバッグが1個 \( 70 \) 円,ティーバッグが1個 \( 40 \) 円であり,仕入れの予算は \( 19000 \) 円である。ただし,袋代は考えないものとする。
仕入れの予算を全額使うものとし,仕入れたドリップバッグとティーバッグをそれぞれ余りなく袋に入れて,2種類の商品を合計 \( 100 \) 袋つくる。
このとき,ドリップバッグとティーバッグをそれぞれ何個仕入れればよいか。 ドリップバッグを \( x \) 個,ティーバッグを \( y \) 個仕入れるものとして,連立方程式をつくり, ドリップバッグとティーバッグの個数をそれぞれ求めなさい。
【解答】
\( \left\{ \begin{array}{}
70x+40y=19000 \\
\dfrac{x}{3}+\dfrac{y}{4}=100 \\
\end{array} \right. \)
これを解くと,\( x=180,y=160 \)
よって,仕入れる量は
ドリップバッグが \( 180 \) 個
ティーバッグが \( 160 \) 個
【解説】
\( \left\{ \begin{array}{}
70x+40y=19000 \;\; ・・・ ➀ \\
\dfrac{x}{3}+\dfrac{y}{4}=100 \;\; ・・・ ➁ \\
\end{array} \right. \)
➀より,
\( 7x+4y=1900 \) ・・・ ➀’
➁ \( \times 12 \) すると,
\( 4x+3y=1200 \) ・・・ ➁’
➀’\( \times 3 \) \( – \) ➁’\( \times 4 \)
\( 5x=900 \)
\( x=180 \)
➁ に代入すると,
\( \dfrac{180}{3}+\dfrac{y}{4}=100 \)
\( \dfrac{y}{4}=40 \)
\( y=160 \)
大問7
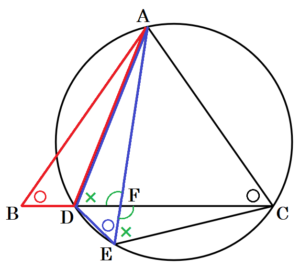
図1のような \( AB=AC \) である二等辺三角形の紙 \( ABC \) がある。この紙 \( ABC \) において,図2のように辺 \( BC \) 上に,\( ∠ADC<90° \) となる点 \( D \) をとる。図3のように線分 \( AD \) で折り返し,頂点 \( B \) が移った点を \( E \),線分 \( AE \) と線分 \( CD \) の交点を \( F \) とする。図4は,図2と図3の点 \( A,B,C,D,E,F \) を結んでできた図形である。
次の(1),(2)に答えなさい。
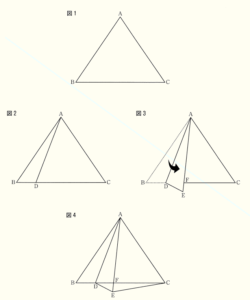
(1) 図4において,\( △ADF \) ∽ \( △CEF \) であることを証明しなさい。
【解答】
\( △ADF \) と \( △CEF \) において,
対頂角は等しいので,
\( ∠AFD=∠CFE \) ・・・ ➀
\( △ABC \) は二等辺三角形なので,
\( ∠ABD=∠ACD \) ・・・ ➁
折り返した図形は合同なので,
\( ∠ABD=∠AED \) ・・・ ③
➁③より,
\( ∠ACD=∠AED \) ・・・ ➃
\( ∠ACD,∠AED \) を弧 \( AD \) に対する
円周角と考えると,
➃より,4点 \( A,D,E,C \)は同一円周上にある。
このとき,弧 \( AC \) に対する円周角なので,
\( ∠ADF=∠CEF \) ・・・ ➄
➀➄より,2組の角がそれぞれ等しいので,
\( △ADF \) ∽ \( △CEF \)
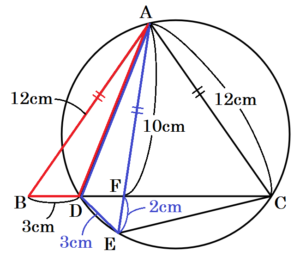
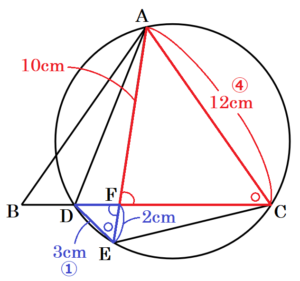
(2) 図4において,\( AB=12 \; cm,BD=3 \; cm,AF=10 \; cm \) であるとき,線分 \( CD \) の長さを求めなさい。
【解答】
\( \dfrac{21}{2} \; cm \)
【解説】
(1)のとおり,4点 \( A,D,E,C \) が同一円周上にあることを利用します。
\( △ABC \) は二等辺三角形なので,
\( AC=AB=12 \; cm \)
折り返した図形は合同なので,
\( ED=BD=3 \; cm,AE=AB=12 \; cm \)
\( AF=10 \; cm \) なので,
\( EF=AE-AF=2 \; cm \)
\( △ACF \) と \( △DEF \) は,
\( ∠ACF=∠DEF,∠AFC=∠DFE \) より,
2組の角がそれぞれ等しいので,
\( △ACF \) ∽ \( △DEF \)
\( AC=12 \; cm,DE=3 \; cm \) より,
相似比は \( 4:1 \)
ここから,
\( AF:DF=4:1 \)
\( 10:DF=4:1 \)
\( DF=\dfrac{5}{2} \; (cm) \)
\( CF:EF=4:1 \)
\( CF:2=4:1 \)
\( CF=8 \; (cm) \)
よって,
\( CD=8+\dfrac{5}{2}=\dfrac{21}{2} \; (cm) \)
大問8
Tさんは, キャンプに行くことにした。
次の(1)~(3)に答えなさい。
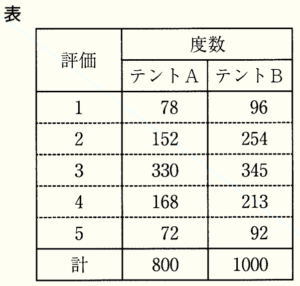
(1) Tさんは,キャンプ場で使用するテントを購入する予定であり,商品とその評価をインターネットで調べた。表は,テントAとテントBのそれぞれの評価を度数分布表にまとめたものであり,評価は,数値が大きいほど高い。
テントAとテントBについて,評価が3以上の相対度数は,どちらが大きいか。評価が3以上の相対度数をそれぞれ明らかにして説明しなさい。ただし,相対度数は,小数第3位を四捨五入し,小数第2位まで求めなさい。
【解答】
評価が3以上の相対度数は,テントAが \( 0.71 \),テントBが \( 0.65 \) なので,
テントAの方が大きい。
【解説】
相対度数は,「求める階級の度数」 \( \div \) 「すべての階級の度数の合計」で求めることができます。
テントAにおいて,
評価が3以上の度数は \( 330+168+72=570 \) なので,
評価が3以上の相対度数は,\( 570 \div 800=0.7125 \) であり,
小数第3位を四捨五入すると,\( 0.71 \)
テントBにおいて,
評価が3以上の度数は \( 345+213+92=650 \) なので,
評価が3以上の相対度数は,\( 650 \div 1000=0.65 \)
(2) Tさんが行こうとしているキャンプ場の標高は \( 350 \; m \) で山の中腹にある。山頂の標高は \( 800 \; m \) であり,Tさんはキャンプ場の気温をもとに,山頂の気温を求めることにした。
気温は,標高が高くなるにつれ一定の割合で下がり,その割合は,標高 \( 100 \; m \) あたり \( 0.6 \; ^\circ \)\( C \) とする。キャンプ場の気温が \( 20.8 \; ^\circ \)\( C \) であるときの山頂の気温を求めなさい。
【解答】
\( 18.1 \; (^\circ \)\( C) \)
【解説】
山頂はキャンプ場よりも \( 800-350=450 \; (m) \) 高い場所になります。
標高 \( 100 \; m \) あたり \( 0.6 \; ^\circ \)\( C \) 気温が下がるので,
標高が \( 400 \; m \) 高くなると,\( 0.6 \times 4=2.4 \; ^\circ \)\( C \),
標高が \( 50 \; m \) 高くなると,\( 0.6 \times \dfrac{1}{2}=0.3 \; ^\circ \)\( C \) 気温が下がります。
つまり,山頂の気温はキャンプ場の気温より \( 2.4+0.3=2.7 \; ^\circ \)\( C \) 低いので,
\( 20.8-2.7=18.1 \; (^\circ \)\( C) \)
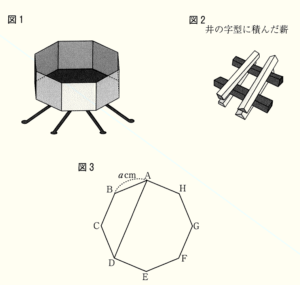
(3) Tさんは,キャンプ場で使用する図1のようなたき火台を購入する予定である。Tさんはその中に入れる薪を,図2のように井の字型に積もうと考えている。
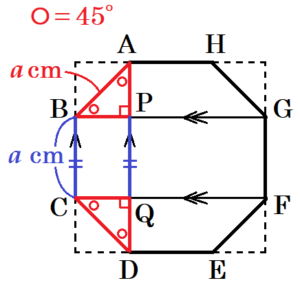
たき火台の底は図3のような正八角形 \( ABCDEFGH \) の形をしていて,Tさんは,その正八角形の対角線 \( AD \) の長さを, たき火台に入れる薪の長さの目安にしようとしている。
正八角形 \( ABCDEFGH \) の一辺の長さを \( a \; cm \) とするとき,対角線 \( AD \) の長さを,\( a \) を使った式で表しなさい。
【解答】
\( (1+\sqrt{2})a \; cm \)
【解説】
正八角形は,正方形の4すみから合同な直角二等辺三角形を切り取った形になっています。
対角線 \( AD \) と対角線 \( BG \) の交点を点 \( P \),
対角線 \( AD \) と対角線 \( CF \) の交点を点 \( Q \)
とすると,
\( △ABP \) は斜辺 \( AB=a \; cm \) の直角二等辺三角形
なので,
\( AP=\dfrac{AB}{\sqrt{2}}=\dfrac{\sqrt{2}a}{2} \; (cm) \)
\( △DCQ≡△ABP \) なので,
\( DQ=AP=\dfrac{\sqrt{2}a}{2} \; cm \)
また,\( BC//AD,BG//CF \) なので,
\( PQ=BC=a \; cm \)
以上より,
\( CD=\dfrac{\sqrt{2}a}{2}+a+\dfrac{\sqrt{2}a}{2} \)
\( =(1+\sqrt{2})a \; (cm) \)