大問1
1 \( 6-(-7) \)
【解説】
\( =6+7 \)
\( =13 \)
2 \( 14 \div \left( -\dfrac{7}{2} \right) \)
【解説】
\( =14 \times \left( -\dfrac{2}{7} \right) \)
\( =-4 \)
3 \( -2^2+(-5)^2 \)
【解説】
\( =-4+25 \)
\( =21 \)
4 \( \sqrt{8}-3\sqrt{6} \times \sqrt{3} \)
【解説】
\( =2\sqrt{2}-3\sqrt{18} \)
\( =2\sqrt{2}-9\sqrt{2} \)
\( =-7\sqrt{2} \)
5 \( 9x^2y \times 4x \div (-8xy) \)
【解答】
\( -\dfrac{9}{2}x^2 \)
【解説】
\( =\dfrac{9x^2y \times 4x}{-8xy} \)
\( =-\dfrac{9}{2}x^2 \)
6 \( x(3x+4)-3(x^2+9) \)
【解説】
\( =3x^2+4x-3x^2-27 \)
\( =4x-27 \)
大問2
1 2次方程式 \( x^2-9x-36=0 \) を解きなさい。
【解説】
\( (x+3)(x-12)=0 \)
\( x=-3,12 \)
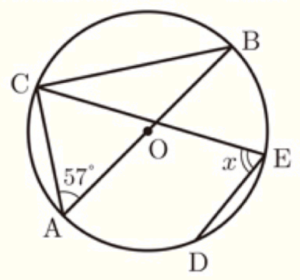
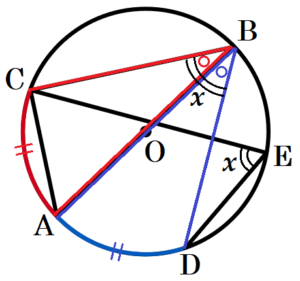
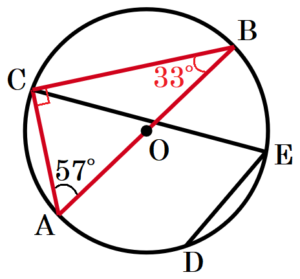
2 右の図において,点 \( C,D,E \) は, \( AB \) を直径とする円 \( O \) の周上の点である。また,弧 \( AC= \) 弧 \( AD \) である。
\( ∠CAB=57° \) のとき,\( ∠x \) の大きさを求めなさい。
【解説】
弧 \( AD \) の円周角なので,\( ∠CED=∠CBD=x \)
また,弧 \( AC= \) 弧 \( AD \) より,\( ∠CBA=∠ABD \)
\( ∠CBD=∠CBA+∠ABD=x \) なので,\( ∠CBA=\dfrac{x}{2} \)
\( △ABC \) において,直径 \( AB \) の円周角なので,\( ∠ACB=90° \)
仮定より,\( ∠CAB=57° \)
よって,\( ∠CBA=180°-(∠CAB+∠ACB)=33° \)
\( ∠CBA=\dfrac{x}{2} \) より,
\( \dfrac{x}{2}=33° \)
\( x=66° \)
3 \( y \) は \( x \) に反比例し,\( x=4 \) のとき \( y=-5 \) である。このときの比例定数を求めなさい。
【解説】
反比例を表す式は \( y=\dfrac{a}{x} \) (\( a \) は比例定数)になります。
ここに,\( x=4,y=-5 \) を代入すると,
\( -5=\dfrac{a}{4} \)
\( a=-20 \)
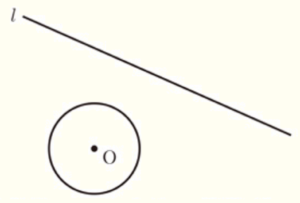
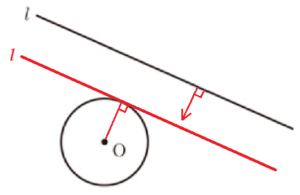
4 右の図において,円 \( O \) の周上にあって,直線 \( l \) からの距離が最も短い点を作図によって求めなさい。そのとき,求めた点を ● で示しなさい。
ただし,作図には定規とコンパスを用い,作図に用いた線は消さずに残しておくこと。
【解説】
直線 \( l \) を垂直な方向に円 \( O \) に近づけ,最初に円と接するとき,
直線 \( l \) は円 \( O \) の接線になります。
円の中心を通る直線と接線は接点で垂直に交わるので,
点 \( O \) から,直線 \( l \) に垂線をひいたときの円との交点が
求める点になります。
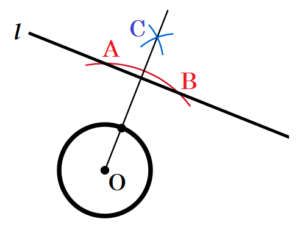
手順1 点 \( O \) を中心として,直線 \( l \) と交わるように弧を描く。
(交点を点 \( A,B \) とします。)
手順2 点 \( A,B \) を中心として,等しい半径で弧を描く。
(交点を点 \( C \) とします。)
手順3 点 \( O,C \) を通る直線を描く。
手順3の直線と円 \( O \) の交点が求める点になります。
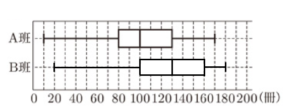
5 あるクラスで生徒の家にある本の冊数を調べた。15人ずつA班とB班に分け,それぞれの班のデータを集計した。図は,A班のデータの分布のようすを箱ひげ図に表したものである。
このとき,次の(1) ,(2)に答えなさい。
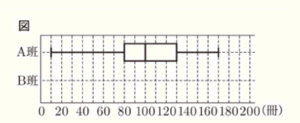
(1) 図において,A班の箱ひげ図から四分位範囲を求めなさい。
【解説】
四分位範囲 \( = \) 第三四分位数 \( – \) 第一四分位数 で求めることができます。
(2) 下のデータは,B班のデータを小さい方から順に整理したものである。このデータをもとに,B班のデータの分布のようすを表す箱ひげ図をかき入れなさい。

【解説】
B班の人数は15人なので,
第一四分位数:少ない方から4番目,中央値:少ない方から8番目,第三四分位数:多い方から4番目
になります。
よって,最小値:20冊,第一四分位数:100冊,中央値:130冊,第三四分位数:160冊,
最大値:180冊 になります。

大問3
ある中学校では,芸術鑑賞会を体育館で行うことになり,生徒会役員のAさんは,そのための準備をしている。このことに関する次の問題に答えなさい。
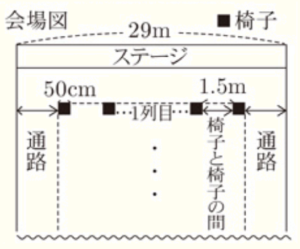
1 Aさんは,体育館の椅子の並べ方を検討している。右の会場図のように体育館の左右に同じ幅で通路を作り,椅子と椅子の間が等間隔になるように椅子を並べることにした。椅子と椅子の間の長さは,\( 1.5 \;m \) とることになっている。Aさんは,生徒がステージをよく見ることができるように横にできるだけ多くの椅子を並べようと考えている。体育館の横の長さは \( 29 \;m \),使う椅子の横幅はすべて \( 50 \; cm \) であることがわかっている。
1列目に並べる椅子の数と通路の横幅の関係については,次の式で表すことができ,Aさんは,その式を用いて
1列目に並べる椅子の数と通路の横幅を検討することにした。
Aさんが検討に用いた式
1列目に並べる椅子の数を \( x \) 脚,通路の横幅を \( y \; m \) としたとき
\( 0.5x+1.5(x-1)+2y=29 \)
このとき,次の(1) ,(2) に答えなさい。
(1) Aさんが検討に用いた式の \( (x-1) \) が表しているものを次のア~エから1つ選び,その記号を書きなさい。
ア 1列目に並べる椅子の数
イ 椅子と椅子の間の長さ
ウ 椅子と椅子の間の数
エ 椅子と椅子の間の長さの和
(2) Aさんが1列目に椅子を12脚並べようとしていたところに,「演出の都合上,左右の通路の横幅をそれぞれ \( 3.5 \; m \) は確保してほしい」という連絡があった。1列目に椅子を12脚並べたとき,通路の横幅を \( 3.5 \; m \) とることができるか。次のア,イから正しいものを1つ選び,その記号を書きなさい。また,それが正しいことの理由をAさんが検討に用いた式をもとに根拠を示して説明しなさい。
ア 通路の横幅を \( 3.5 \; m \) とることができる。 イ 通路の横幅を \( 3.5 \; m \) とることができない。
【解答】
記号:イ
\( 0.5x+1.5(x-1)+2y \) に \( x=12,y=3.5 \) を代入すると,
\( 0.5 \times 12+1.5 \times (12-1)+2 \times 3.5=6+16.5+7=29.5 \)
となり,通路の横幅を \( 3.5 \; m \) とるためには,\( 29.5 \;m \) 必要である。
体育館の横の長さは \( 29 \;m \) しかないので,通路の横幅を3.5mとることができない。
2 生徒会役員Aさん,Bさん,Cさん,Dさん,Eさん,Fさんの6人の中から,芸術鑑賞会当日に花束贈呈を担当する人を2人選ぶことになった。花束贈呈を担当する2人については,次の方法で選ぶ。
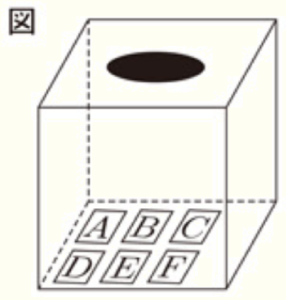
右の図のように,箱の中に6人それぞれの名前が書かれたカードが1枚
ずつ入っている。箱の中のカードをよくかきまぜてから,一度に2枚の
カードを取り出し,カードに名前が書かれている人が花束贈呈を担当する。
ただし,どのカードを取り出すことも同様に確からしいものとする。
このとき,次の(1) ,(2) に答えなさい。
(1) 6人の中から花束贈呈を担当する2人を選ぶときの選び方は,全部で何通りあるか求めなさい。
【解説】
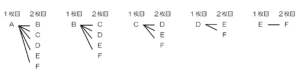
2人の選び方の組み合わせを樹形図に書いてみると,下の図のようになり,15通り
(2) Aさん,Bさんのどちらも花束贈呈の担当に選ばれない確率を求めなさい。
【解説】
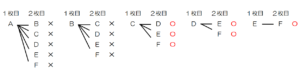
(1) の樹形図において,A,Bどちらも選ばれない組み合わせに
○ ,A,Bどちらか,または両方が
選ばれる組み合わせに ✕ をつけます。
A,Bどちらも選ばれない組み合わせは6通りなので,
求める確率は \( \dfrac{6}{15}=\dfrac{2}{5} \)
大問4
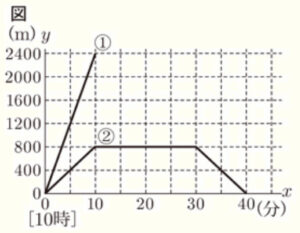
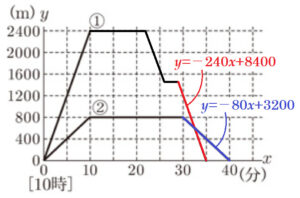
姉と弟は,母の誕生日パーティーの準備をしている。2人は \( 10 \) 時に自宅を出発し,姉は自転車で花屋とケーキ屋へ,弟は徒歩で雑貨屋へ買い物をするために出かけた。姉は雑貨屋の前とケーキ屋の前を通過し,花屋で買い物をしてから,帰りにケーキ屋で買い物をした。次の資料は,各地点の間の道のりと2人の移動のようすを示したものである。ただし,2人は同じ道を往復することとし,どの区間でも移動する速さは,それぞれ一定であるものとする。
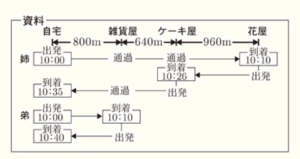
図の ➀ は,姉が移動するようすについて,\( 10 \) 時 \( x \) 分の地点から自宅までの道のりを \( y \; m \) として,\( x \) と \( y \) の関係を表したグラフの一部である。また,図の ➁ は,弟が移動するようすについて,\( 10 \) 時 \( x \) 分の地点から自宅までの道のりを \( y \; m \) として,\( x \) と \( y \) の関係を表したグラフである。
このとき,次の1~4に答えなさい。
1 2人が出発してから \( 5 \) 分経過したとき,姉のいる地点と弟のいる地点の道のりの差を図のグラフから求めることができる。その方法を説明しなさい。ただし,実際に道のりの差を求める必要はない。
【解答】
\( x=5 \) のときの ➀,➁ の \( y \) 座標の値を求め,その差を求める
2 図の ➁ について,\( x \) の変域が \( 0≦x≦10 \) のとき,\( y \) を \( x \) の式で表しなさい。
3 姉が花屋とケーキ屋に滞在していた時間をそれぞれ求めなさい。
【解答】
花屋 ・・・ \( 12 \) 分
ケーキ屋 ・・・ \( 3 \) 分
【解説】
自宅から花屋までの \( 2400 \; m \) を \( 10 \) 分で移動しているので,
分速 \( \dfrac{2400}{10}=240 \; m \) で移動していることになります。
このとき,花屋からケーキ屋までの \( 960 \; m \) を移動するのにかかる時間は,
\( \dfrac{960}{240}=4 \) 分 になります。
ケーキ屋に到着したのは \( 10 \) 時 \( 26 \) 分なので,花屋を出発したのは,\( 10 \) 時 \( 22 \) 分
よって,花屋に滞在していた時間は,\( 10 \) 時 \( 10 \) 分から \( 22 \) 分までの \( 12 \) 分間
また,ケーキ屋から自宅までかかる時間は,\( 10-4=6 \) 分
自宅に到着したのは \( 10 \) 時 \( 35 \) 分なので,ケーキ屋を出発したのは,\( 10 \) 時 \( 29 \) 分
よって,ケーキ屋に滞在していた時間は,\( 10 \) 時 \( 26 \) 分から \( 29 \) 分までの \( 3 \) 分間
4 弟は,雑貨屋から自宅まで帰る途中で姉に追い越された。追い越された地点から自宅までの道のりを求めなさい。
【解説】
姉が花屋から自宅まで移動するようすをグラフに書き足すと,姉に追い越された時間と場所は ➀ と ➁ の直線の交点として表れます。
右の図の赤の直線の式を \( y=-240x+b \) とすると,
\( 35,0 \) を通るので,代入すると,
\( 0=-240 \times 35+b \)
\( b=8400 \)
よって,赤の直線の式は,\( y=-240x+8400 \)
同様に青の直線の式を \( y=-80x+c \) とすると,
\( (40,0) \) を通るので,代入すると,
\( 0=-80 \times 40+c \)
\( c=3200 \)
よって,青の直線の式は,\( y=-80x+3200 \)
2つの直線の式を連立方程式として解くと,
\( (x,y)=\left( \dfrac{65}{2},600 \right) \)
よって,追い越された地点から自宅までの道のりは,\( 600 \; m \)
連立方程式の途中式
\( \left\{ \begin{array}{}
y=-240x+8400 \\
y=-80x+3200
\end{array} \right. \)
\( -240x+8400=-80x+3200 \)
\( 160x=5200 \)
\( x=\dfrac{65}{2} \)
\( y=-80 \times \dfrac{65}{2}+3200 \)
\( =600 \)
大問5
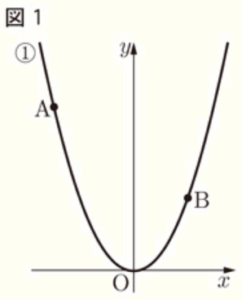
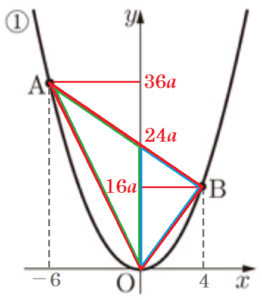
1 図1において,➀ は関数 \( y=ax^2 (a>0) \) のグラフであり,点 \( A,B \) は ➀ 上にある。
点 \( A,B \) の \( x \) 座標はそれぞれ \( -6,4 \) である。
このとき,次の(1) ,(2)に答えなさい。
(1) \( a=\dfrac{1}{4} \) のとき,直線 \( AB \) の式を求めなさい。
【解答】
\( y=-\dfrac{1}{2}x+6 \)
【解説】
点 \( A \) の \( y \) 座標は,\( y=\dfrac{1}{4} \times (-6)^2=9 \)
点 \( B \) の \( y \) 座標は,\( y=\dfrac{1}{4} \times 4^2=4 \)
直線 \( AB \) は,\( A(-6,9),B(4,4) \) を通るので,
傾き \( =\dfrac{4-9}{4-(-6)}=-\dfrac{1}{2} \)
直線 \( AB \) の式を \( y=-\dfrac{1}{2}x+b \) とし,
\( x=4,y=4 \) を代入すると,
\( 4=-\dfrac{1}{2} \times 4+b \)
\( b=6 \)
よって,直線 \( AB \) の式は,\( y=-\dfrac{1}{2}x+6 \)
(2) \( △AOB \) の面積が \( 20 \) になるときの \( a \) の値を求めなさい。
【解答】
\( a=\dfrac{1}{6} \)
【解説】
点 \( A \) の \( y \) 座標は,\( y=a \times (-6)^2=36a \)
点 \( B \) の \( y \) 座標は,\( y=a \times 4^2=16a \)
直線 \( AB \) は,\( A(-6,36a),B(4,16a) \) を通るので,
傾き \( =\dfrac{16a-36a}{4-(-6)}=-2a \)
直線 \( AB \) の式を \( y=-2ax+b \) とし,
\( x=4,y=16a \) を代入すると,
\( 16a=-2a \times 4+b \)
\( b=24a \)
直線 \( AB \) と \( y \) 軸の交点を点 \( C \) とし,線分 \( OC \) を底辺と考えると,
\( △AOC \)の高さは \( 6 \),\( △BOC \)の高さは \( 4 \) になるので,
\( △AOB=20 \)
\( △AOC+△BOC=20 \)
\( \left( 24a \times 6 \times \dfrac{1}{2} \right)+\left( 24a \times 4 \times \dfrac{1}{2} \right)=20 \)
\( 72a+48a=20 \)
\( 120a=20 \)
\( a=\dfrac{1}{6} \)
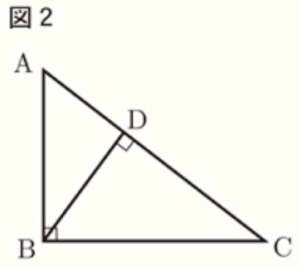
2 図2において,\( △ABC \) は,\( ∠ABC=90° \) の直角三角形である。頂点 \( B \) から辺 \( AC \) に垂線をひき,その交点を \( D \) とする。
このとき,次の(1)~(3)に答えなさい。
(1) \( △ABD \) ∽ \( △BCD \) となることを証明しなさい。
【解答】
\( △ABD \) と \( △BCD \) において,
\( BD⊥AC \) より,\( ∠ADB=∠BDC=90° \) ・・・ ➀
\( △ABD \)は直角三角形なので,\( ∠BAD=90°-∠ABD \) ・・・ ➁
\( ∠ABC=90° \) より,\( ∠CBD=90°-∠ABD \) ・・・ ➂
➁➂より,\( ∠BAD=∠CBD \) ・・・ ④
➀④より,2組の角がそれぞれ等しいので,\( △ABD \) ∽ \( △BCD \)
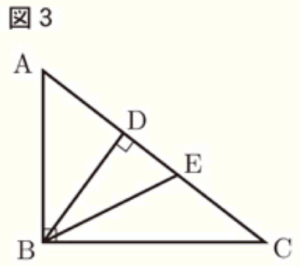
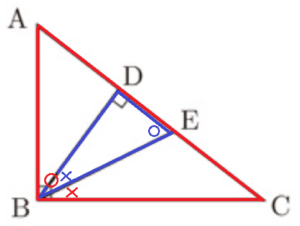
(2) 図3のように,\( ∠DBC \) の二等分線をひいたときの辺 \( AC \) との交点を \( E \) とする。次の説明は,図3において,\( AB=AE \) が成り立つことを示したものである。
\( \fbox{ X } \) と \( \fbox{ Y } \) に当てはまるものを,下のア~カから1つずつ選び,その記号を書きなさい。
説明
\( ∠ABC \) は直角であるから,
\( ∠ABE+∠EBC=90° \) ・・・ ➀
\( △DBE \) は直角三角形であるから,
\( ∠DEB +\fbox{ X } = 90° \) ・・・ ➁
また,仮定より \( ∠EBC= \fbox{ X } \) であるから,
➀,➁より, \( ∠ABE=∠AEB \)
したがって \( △ABE \) において,\( \fbox{ Y } \) から,
\( AB=AE \)
ア \( ∠ABD \) イ \( ∠BCE \) ウ \( ∠DAB \) エ \( ∠DBE \)
オ 2つの辺が等しい三角形は2つの角が等しくなる
カ 2つの角が等しい三角形は二等辺三角形になる
【解答】
\( \fbox{ X } \) ・・・ エ
\( \fbox{ Y } \) ・・・ カ
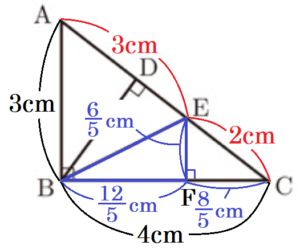
(3) 図3において,\( AB=3 \; cm,BC=4 \; cm \) であるとき,線分 \( BE \) の長さを求めなさい。
【解答】
\( \dfrac{6\sqrt{5}}{5} \; cm \)
【解説】
\( AB=3 \; cm,BC=4 \; cm \) より,\( △ABC \) は,3辺の長さが \( 3:4:5 \) の直角三角形なので,\( AC=5 \; cm \)
(2) より,\( AB=AE \) なので,\( AE=3 \; cm,EC=2 \; cm \)
点 \( E \) から線分 \( BC \) に垂線をひき,交点を点 \( F \) とすると,
\( △ABC \) ∽ \( △EFC \) なので,
\( AB:AC=EF:EC \)
\( 3:5=EF:2 \)
\( EF=\dfrac{6}{5} \; (cm) \)
\( BC:AC=FC:EC \)
\( 4:5=FC:2 \)
\( FC=\dfrac{8}{5} \; (cm) \)
\( BC=4 \; cm \) より,
\( BF=BC-FC=4-\dfrac{8}{5}=\dfrac{12}{5} \; (cm) \)
\( △BEF \) において,三平方の定理より,
\( BE^2=BF^2+EF^2 \)
\( =\left( \dfrac{12}{5} \right)^2+\left( \dfrac{6}{5} \right)^2 \)
\( =\dfrac{144}{25}+\dfrac{36}{25} \)
\( =\dfrac{180}{25} \)
\( BE=\dfrac{6\sqrt{5}}{5} \; (cm) \) (\( BE>0 \)より)
大問6
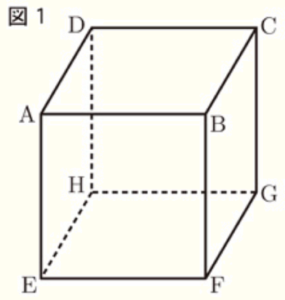
図1のような一辺の長さが \( 8 \; cm \) の立方体 \( ABCD-EFGH \) がある。
このとき,次の1,2に答えなさい。
1 四角形 \( ABCD \) の対角線の長さを求めなさい。
【解答】
\( 8\sqrt{2} \; cm \)
【解説】
\( △ABD \) は \( AB=AD=8 \; cm \) の直角二等辺三角形なので,
\( BD=8\sqrt{2} \; cm \)
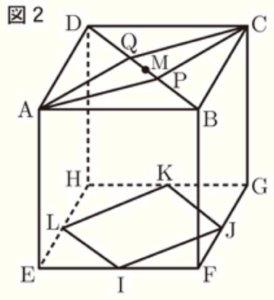
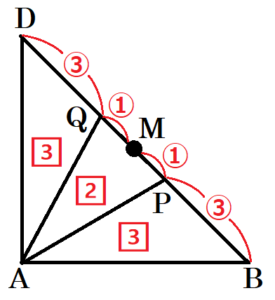
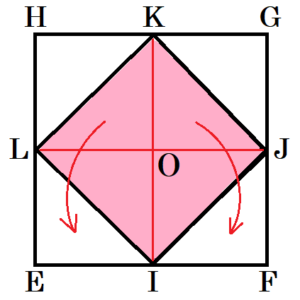
2 図2のように,図1の立方体の辺 \( EF,FG,GH,HE \) の中点にそれぞれ \( I,J,K,L \) をとり,線分 \( BD \) の中点に \( M \) をとる。また,点 \( P \) は \( BP:PM=3:1 \) となる線分 \( BM \) 上の点であり,点 \( Q \) は \( MQ:QD=1:3 \) となる線分 \( MD \) 上の点である。
このとき,次の (1)~(3) に答えなさい。
(1) 四角形 \( APCQ \) と四角形 \( LIJK \) の面積比を最も簡単な整数の比で表しなさい。
【解説】
立方体のすべての面は面積が等しいので,
「四角形 \( APCQ \) と四角形 \( ABCD \) の面積比」,「四角形 \( LIJK \) と四角形 \( EFGH \) の面積比」
を求め,そこから 四角形 \( APCQ \) と四角形 \( LIJK \) の面積比を求めます。
【四角形 \( APCQ \) と四角形 \( ABCD \) の面積比】
四角形 \( APCQ \) は対角線 \( BD \) について線対称なので,
半分だけにあたる \( △APQ \) と \( △ABD \) の比について考えます。
\( BP:PM=3:1,MQ:QD=1:3 \) より,\( BP:PQ:QD=3:2:3 \)
\( △ABP,△APQ,△ADQ \) について,線分 \( BP,PQ,QD \) を底辺とすると,高さが等しいので,線分 \( BP,PQ,QD \) の長さの比が \( △ABP,△APQ,△ADQ \) の面積比と等しくなります。
よって,\( △ABP:△APQ:△ADQ=3:2:3 \)
ここから,\( △APQ:△ABD=2:8=1:4 \) となるので,
四角形 \( APCQ \):四角形 \( ABCD=1:4 \)
つまり,四角形 \( APCQ=\dfrac{1}{4} \) 四角形 \( ABCD \) ・・・ ➀
【四角形 \( LIJK \) と四角形 \( EFGH \) の面積比】
線分 \( IK \) と線分 \( JL \) の交点を \( O \) とすると,
\( △OJK≡△FIJ,△OLK≡△EIL \) なので,これらを入れ替えると,
四角形 \( LIJK= \) 四角形 \( EFJL \) になります。
四角形 \( EFJL \) の面積は四角形 \( EFGH \) の半分にあたるので,
四角形 \( LIJK \):四角形 \( EFGH=1:2 \)
つまり,四角形 \( LIJK=\dfrac{1}{2} \) 四角形 \( EFGH \) ・・・ ➁
➀➁より,四角形 \( APCQ: \) 四角形 \( LIJK=\dfrac{1}{4}:\dfrac{1}{2}=1:2 \)
(2) 3点 \( A,I,M \) を頂点とする \( △AIM \) の面積を求めなさい。
【解説】
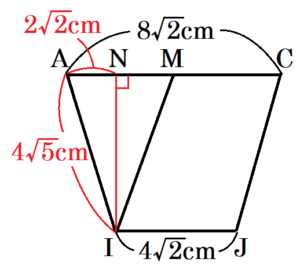
面 \( ACJI \) で切断すると,四角形 \( ACJI \) は
\( AC=8\sqrt{2} \; cm,IJ=4\sqrt{2} \; cm,AI=CJ=4\sqrt{5} \; cm \)
の等脚台形になっています。
点 \( I \) から線分 \( AC \) に垂線をひき,交点を \( N \) とすると,
\( AN=\dfrac{8\sqrt{2}-4\sqrt{2}}{2}=2\sqrt{2} \; cm \)
\( △AIN \) において,三平方の定理より,
\( IN^2=(4\sqrt{5})^2-(2\sqrt{2})^2=72 \)
\( IN=6\sqrt{2} \; (cm) \)
よって,
\( △AIM=AM \times MN \times \dfrac{1}{2} \)
\( =4\sqrt{2} \times 6\sqrt{2} \times \dfrac{1}{2} \)
\( =24 \; (cm^2) \)
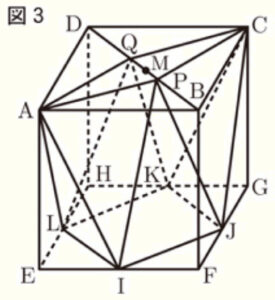
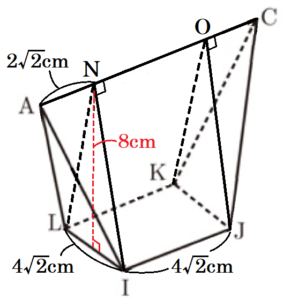
(3) 図3において,図2の8点 \( A,P,C,Q,L,I,J,K \) を頂点とする立体の体積を求めなさい。
【解答】
\( \dfrac{704}{3} \; cm^3 \)
【解説】
3つの立体 \( P-ACJI,Q-ACKL,AC-JKLI \) に分けて求めます。
【四角すい \( P-ACJI \) の体積 】
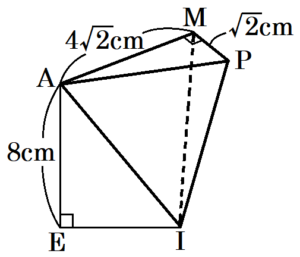
まず,面 \( ACJI \) を底面としたときの高さを求めます。
三角すい \( P-AMI \) において,面 \( AMP \) を底面とすると,
体積は,
三角すい \( P-AMI=\left( 4\sqrt{2} \times \sqrt{2} \times \dfrac{1}{2} \right) \times 8 \times \dfrac{1}{3} \)
\( =\dfrac{32}{3} \; (cm^3) \)
\( △AMI \) を底面としたときの高さを \( h \) とすると,
\( 24 \times h \times \dfrac{1}{3}=\dfrac{32}{3} \)
\( h=\dfrac{4}{3} \; (cm) \)
面 \( AMI,ACJI \) は同一平面なので,面 \( ACJI \) を底面としたときの高さも \( \dfrac{4}{3} \; cm \)
よって,四角すい \( P-ACJI \) の体積は,
四角すい \( P-ACJI=\left\{(4\sqrt{2}+8\sqrt{2}) \times 6\sqrt{2} \times \dfrac{1}{2} \right\} \times \dfrac{4}{3} \times \dfrac{1}{3} \)
\( =32 \; (cm^3) \) ・・・ ➀
【四角すい \( Q-ACKL \) の体積 】
面 \( ACGE \) について,四角すい \( P-ACJI \) と対称なので,\( 32 \; cm^3 \) ・・・ ➁
【立体 \( AC-JKLI \) の体積 】
点 \( J \) から線分 \( AC \) に垂線をひき,交点を \( O \) とし,面 \( NLI,OKJ \) で切断すると,
三角すい \( A-NLI \),三角柱 \( NLI-OKJ \),三角すい \( C-OKJ \) の3つに分けることができます。
三角すい \( A-NLI \) の体積は,
三角すい \( A-NLI=\left( 4\sqrt{2} \times 8 \times \dfrac{1}{2} \right) \times 2\sqrt{2} \times \dfrac{1}{3} \)
\( =\dfrac{64}{3} \; (cm^3) \)
三角すい \( C-OKJ \) の体積は,
三角すい \( A-NLI \) の体積と同じなので,\( \dfrac{64}{3} \; (cm^3) \)
三角柱 \( NLI-OKJ \) の体積は,
三角柱 \( NLI-OKJ=\left( 4\sqrt{2} \times 8 \times \dfrac{1}{2} \right) \times 4\sqrt{2} \)
\( =128 \; (cm^3) \)
よって,立体 \( AC-JKLI \) の体積は,
立体 \( AC-JKLI=\dfrac{64}{3}+\dfrac{64}{3}+128 \)
\( =\dfrac{512}{3} \; (cm^3) \) ・・・ ➂
➀➁➂より,立体 \( APCQ-LIJK=32+32+\dfrac{512}{3}=\dfrac{704}{3} \; (cm^3) \)