大問1
(1) \( 9+4 \times (-3) \) を計算せよ。
【解説】
\( =9-12 \)
\( =-3 \)
(2) \( 2(5a+4b)-(a-6b) \) を計算せよ。
【解説】
\( =10a+8b-a+6b \)
\( =9a+14b \)
(3) \( \dfrac{18}{\sqrt{3}}-\sqrt{27} \) を計算せよ。
【解説】
\( =\dfrac{18 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}-3\sqrt{3} \)
\( =6\sqrt{3}-3\sqrt{3} \)
\( =3\sqrt{3} \)
(4) 2次方程式 \( (x-5)(x+4)=3x-8 \) を解け。
【解説】
\( x^2-x-20=3x-8 \)
\( x^2-4x-12=0 \)
\( (x+2)(x-6)=0 \)
\( x=-2,6 \)
(5) \( 1 \) から \( 6 \) までの目が出る2つのさいころ \( A,B \) を同時に投げるとき,出る目の数の積が偶数になる確率を求めよ。
ただし,さいころはどの目が出ることも同様に確からしいとする。
【解説】
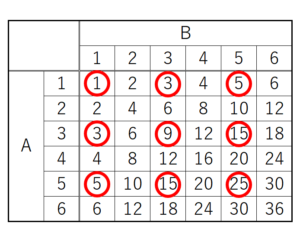
2つのさいころ \( A,B \) の出た目の組み合わせとその積を表に書いて,奇数になるところに
○ をつけてみます。
奇数になる組み合わせは9通り,すべての組み合わせは36通りなので,
積が奇数になる確率は,\( \dfrac{9}{36}=\dfrac{1}{4} \)
よって,積が奇数になる確率は,\( 1-\dfrac{1}{4}=\dfrac{3}{4} \)
【別解】
奇数 \( \times \) 奇数 \( = \) 奇数
奇数 \( \times \) 偶数 \( = \) 偶数
偶数 \( \times \) 奇数 \( = \) 偶数
偶数 \( \times \) 偶数 \( = \) 偶数
なので,積が奇数になるのは,
出た目が両方とも奇数のとき
とわかります。
\( (a,b)=(1,1),(1,3),(1,5) \)
\( (3,1),(3,3),(3,5) \)
\( (5,1),(5,3),(5,5) \)
(6) 関数 \( y=-2x+7 \) について,\( x \) の値が \( -1 \) から \( 4 \) まで増加するときの \( y \) の増加量を求めよ。
【解説】
\( x=-1 \) のとき,\( y \) の値は,\( y=-2 \times (-1)+7=9 \)
\( x=4 \) のとき,\( y \) の値は,\( y=-2 \times 4+7=-1 \)
よって,\( y \) の増加量は,\( -1-9=-10 \)
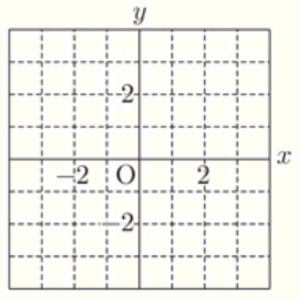
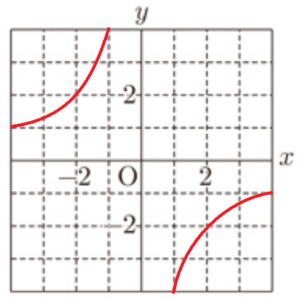
(7) 関数 \( y=-\dfrac{4}{x} \) のグラフをかけ。
【解説】
反比例のグラフは,原点について点対称な曲線も
あるので,2本の曲線を書く必要があります。
\( x=1 \) のとき,\( y=-\dfrac{4}{1}=-4 \)
\( x=2 \) のとき,\( y=-\dfrac{4}{2}=-2 \)
\( x=4 \) のとき,\( y=-\dfrac{4}{4}=-1 \)
なので,この3点を曲線でつなぎます。
\( x=-1 \) のとき,\( y=-\dfrac{4}{-1}=4 \)
\( x=-2 \) のとき,\( y=-\dfrac{4}{-2}=2 \)
\( x=-4 \) のとき,\( y=-\dfrac{4}{-4}=1 \)
なので,この3点も曲線でつなぎます。
(8) M中学校の全校生徒450人の中から無作為に抽出した40人に対してアンケートを行ったところ,家で,勉強のためにICT機器を使用すると回答した生徒は32人であった。M中学校の全校生徒のうち,家で,勉強のためにICT機器を使用する生徒の人数は,およそ何人と推定できるか答えよ。
【解説】
無作為に抽出するということは,サンプルをどこからとっても比率(割合)は同じであると考えます。
よって,40人中32人が機器を使用するとき,同じ比率(割合)で450人全体の中にも機器を使用する人がいると考えるので,比で表すと,
\( 40:32=450:x \)
\( 40x=450 \times 32 \)
\( x=45 \times 8=360 \)(人)
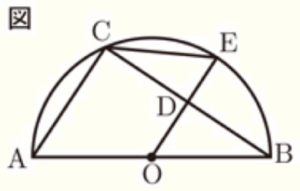
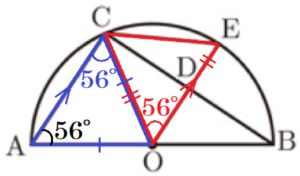
(9) 図のように,線分 \( AB \) を直径とする半円 \( O \) の弧 \( AB \) 上に点 \( C \) をとり,\( △ABC \) をつくる。線分 \( AC \) に平行で点 \( O \) を通る直線と線分 \( BC \),弧 \( BC \) との交点をそれぞれ \( D,E \) とし,点 \( C \) と点 \( E \) を結ぶ。 \( ∠CAB=56° \) のとき,\( ∠DEC \) の大きさを求めよ。
【解説】
補助線 \( OC \) をひくと,\( △OAC,△OCE \) は二等辺三角形であることに注目します。
\( △OAC \) は,\( OA=OC \) の二等辺三角形なので,
\( ∠OCA=∠OAC=56° \)
\( AC//OE \) より,錯角は等しいので,
\( ∠COE=∠OCA=56° \)
\( △COE \) は,\( OC=OE \) の二等辺三角形なので,
\( ∠DEC=\dfrac{180°-∠COE}{2}=62° \)
大問2
あめを買いに行く。
次の (1),(2) に答えよ。
(1) あめは,定価の \( 20 \) %引きの \( a \) 円で売られている。
このとき,あめの定価を \( a \) を用いた式で表せ。
【解説】
この関係を方程式で表すと,
定価 \( \times \left( 1-\dfrac{20}{100} \right)=a \)
定価 \( \times \dfrac{4}{5}=a \)
定価 \( =a \times \dfrac{5}{4}=\dfrac{5}{4}a \)
(2) あめを買い,その全てを何人かの生徒で分ける。
あめを生徒1人に5個ずつ分けると8個余り,生徒1人に7個ずつ分けると10個たりない。
このとき,あめを生徒1人に6個ずつ分けるとすると,あめはたりるか説明せよ。
説明する際は,あめの個数と生徒の人数のどちらかを \( x \) として (どちらを \( x \) としてもかまわない。) つくった方程式を示し,あめの個数と生徒の人数を求め,その数値を使うこと。
【解答】
生徒の人数を \( x \) 人とすると,
あめを生徒1人に5個ずつ分けたときのあめの個数は \( 5x+8 \)(個)
あめを生徒1人に7個ずつ分けたときのあめの個数は \( 7x-10 \)(個)
と表すことができる。
買ったあめの個数はかわらないので,
\( 5x+8=7x-10 \)
\( 2x=18 \)
\( x=9 \)
よって,生徒の人数は9人。
また,買ったあめの個数は,
\( 7 \times 9-10=53 \)
より,53個。
生徒1人に6個ずつ分けるとき,必要なあめの個数は
\( 6 \times 9=54 \)
より,54個なので,あめはたりない。
大問3
農園に3つの品種 A,B,C のいちごがある。孝さんと鈴さんは,3つの品種のいちごの重さを比べるために,A~C のいちごをそれぞれ30個ずつ集め,1個ごとの重さのデータを図1のように箱ひげ図に表した。
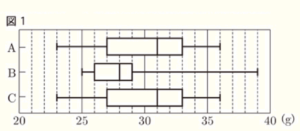
下の会話文は,孝さんと鈴さんが,図1をもとに,「重いいちごの個数が多いのは,A~Cのどの品種といえるか」について,会話した内容の一部である。
孝さん:AとCは,箱ひげ図が同じ形だから,①範囲や四分位範囲などが異なる AとBを比べたいけど,
どうやって比べたらいいかな。
鈴さん:基準となる重さを決めて,比べたらどうかな。例えば,基準を \( 25 \; g \) にすると,\( 25 \; g \) 以上の個数は,
Bの方がAより多いといえるよ。図1から,個数の差が1個以上あるとわかるからね。
孝さん:基準を \( 34 \; g \) にしても,\( 34 \; g \) 以上の個数は,ひげの長さの違いだけではわからないから,
AとBのどちらが多いとはいえないなあ。
鈴さん:基準を \( 30 \; g \) にすると,\( 30 \; g \) 以上の個数は,Aの方がBより多いといえるよ。
孝さん:➁図1から,\( 30 \; g \) 以上の個数は,Aが15個以上,Bが7個以下とわかるからだね。
鈴さん:箱ひげ図を見て基準を決めると,重いいちごの個数が多いのは,AとBのどちらであるか
比べられるね。では,箱ひげ図が同じ形の ➂AとCのデータの分布の違いをヒストグラムで
見てみようよ。
次の (1)~(3) に答えよ。
(1) 下線部➀について,Aのデータの範囲とAのデータの四分位範囲を求めよ。
【解答】
範囲 ・・・ \( 13 \; g \)
四分位範囲 ・・・ \( 6 \; g \)
【解説】
範囲は 最大値 \( – \) 最小値 で求めることができます。 \( 36-23=13 \; (g) \)
四分位範囲は 第三四分位数 \( – \) 第一四分位数 で求めることができます。 \( 33-27=6 \; (g) \)
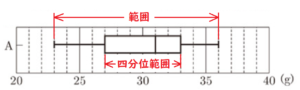
(2) 下線部➁は,次の2つの値と基準の \( 30 \; g \) を比較した結果からわかる。
Aのデータの【X】 Bのデータの【Y】
【X】,【Y】は,それぞれ次の ア~カ のいずれかである。【X】,【Y】をそれぞれ1つずつ選び,
記号をかけ。また,Aのデータの【X】とBのデータの【Y】を数値で答えよ。
ア 最小値 イ 第1四分位数 ウ 中央値
エ 平均値 オ 第3四分位数 カ 最大値
【解答】
Aのデータの【X】・・・ ウ \( 31 \; g \)
Bのデータの【Y】・・・ オ \( 29 \; g \)
【解説】
各品種とも30個の重さを量ったので,
中央値は,重い方から14番目と15番目の重さの平均値,
第三四分位数は重い方から8番目の値になります。
Aの中央値は \( 31 \; g \) なので,重い方から15番目の重さは \( 31 \; g \) 以上です。
Bの第三四分位数は \( 29 \; g \) なので,重い方から8番目の重さは \( 29 \; g \) であり,
\( 30 \; g \) 以上になのは,7個以下とわかります。
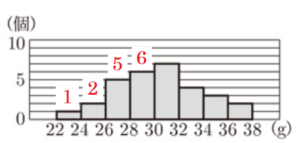
(3) 下線部➂について,図2は,Aのデータをヒストグラムに表したものであり,例えば,Aの重さが \( 22 \; g \) 以上 \( 24 \; g \) 未満の個数は1個であることを表している。
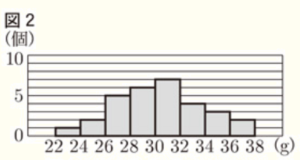
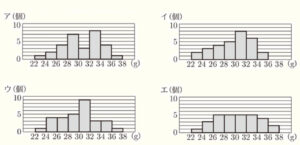
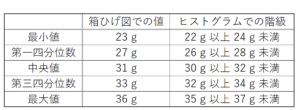
図2において,重さが \( 30 \; g \) 未満の累積度数を求めよ。また,Cのデータをヒストグラムに表したものが,次のア~エに1つある。それを選び,記号をかけ。
【解説】
【\( 30 \; g \) 未満の累積度数】
\( 30 \; g \) 未満のすべての階級の度数の合計が求める累積度数になります。
すべての階級について,度数を
図2に書き加えました。
度数の合計は,\( 1+2+5+6=14 \)(個)
【Cを表すヒストグラムはどれか?】
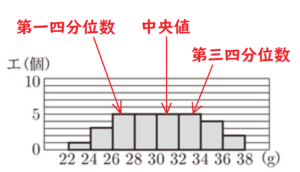
Cの箱ひげ図から,最小値,第一四分位数,中央値,第三四分位数,最大値のそれぞれの値と,
ヒストグラムにしたときにあてはまる階級は下の表のとおりです。
これらがすべてあてはまるヒストグラムは,エになります。
大問4
東西に一直線にのびた道路上にP地点がある。
バスは,P地点に停車しており,この道路を東に向かって進む。次の式は,バスがP地点を出発してから \( 30 \) 秒後までの時間と進む道のりの関係を表したものである。
式 バスについての時間(秒)と道のり \( (m) \)
\( ( \)道のり\( ) \) \( =\dfrac{1}{4} \times \) \( ( \)時間\( )^2 \)
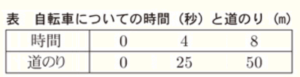
自転車は,P地点より西にある地点から,この道路を東に向かって,一定の速さで進んでいる。自転車は,バスがP地点を出発すると同時にP地点を通過し,その後も一定の速さで進む。次の表は,自転車がP地点を通過してから \( 8 \) 秒後までの時間と進む道のりの関係を表したものである。
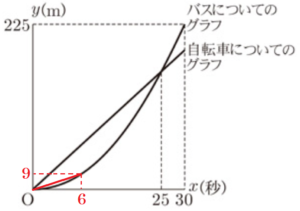
下の図は,バスがP地点を出発してから \( 30 \) 秒後までの時間を横軸( \( x \) 軸),P地点から進む道のりを縦軸( \( y \) 軸)として,バスについての時間と道のりの関係をグラフに表したものに,自転車の進むようすをかき入れたものであり,バスは,P地点を出発してから \( 25 \) 秒後に自転車に追いつくことを示している。
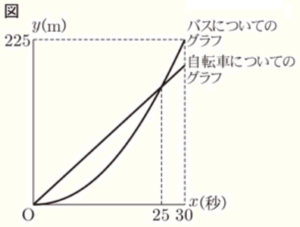
次の (1)~(3) に答えよ。
(1) バスについてのグラフ上にある2点 \( (0, 0) \) と \( (6, 9) \) を直線で結ぶ。この直線の傾きは,バスについての何を表しているか。正しいものを次のア~エから1つ選び,記号をかけ。
ア P地点を出発してから \( 6 \) 秒間で進む道のり
イ P地点を出発してから \( 9 \) 秒間で進む道のり
ウ P地点を出発してから \( 6 \) 秒後までの平均の速さ
エ P地点を出発してから \( 9 \) 秒後までの平均の速さ
【解説】
\( (0, 0) \) と \( (6, 9) \) を直線で結ぶということは,
\( 1 \) 秒あたり同じ距離ずつ進むということを
\( 6 \) 秒間続けていることを表しています。
つまり,これは,\( 6 \) 秒後までの平均の速さを
表していることになります。
(2) この道路上に,P地点から東に \( 100 \; m \) 離れたQ地点がある。バスがQ地点を通過するのは,自転車がQ地点を通過してから何秒後か求めよ。
【解説】
式より,バスが進む状態を表す式は \( y=\dfrac{1}{4}x^2 \) なので,\( y=100 \) を代入すると,
\( 100=\dfrac{1}{4}x^2 \)
\( x^2=400 \)
\( x=20 \)(秒後) ( \( x>0 \)より )
表より,自転車が進む状態を表す式は,\( y=\dfrac{25}{4}x \) なので,\( y=100 \) を代入すると,
\( 100=\dfrac{25}{4}x \)
\( 25x=400 \)
\( x=16 \)(秒後)
よって,答えは,\( 20-16=4 \)(秒後)
(3) タクシーは,この道路を東に向かって,秒速 \( 10 \; m \) で進むものとする。タクシーは,バスがP地点を出発した \( 10 \) 秒後にP地点を通過する。
このとき,タクシーは,バスより先に自転車に追いつくことができるか次のように説明した。
説明
タクシーとバスのそれぞれが自転車に追いつくのは,バスがP地点を出発してから,タクシーが T 秒後で,バスが \( 25 \) 秒後である。
T は \( 25 \) より ➀(ア 大きい イ 小さい) ので,タクシーは,バスより先に自転車に追いつくことが ➁(ウ できる エ できない)。
説明のTにあてはまる数を求め,下線部➀,➁の ( ) にあてはまるものを,それぞれ1つ選び,記号をかけ。
【解答】
T ・・・ \( \dfrac{80}{3} \) 秒後
下線部 ➀ ・・・ ア
下線部 ➁ ・・・ エ
【解説】
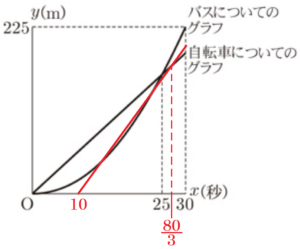
グラフの中に,タクシーが進む状態を表す直線を書き足します。
タクシーは秒速 \( 10 \; m \) で進むことから,
この直線の式を \( y=10x+b \) とすると,
\( (10, 0) \) を通るので,
\( 0=10 \times 10+b \)
\( b=-100 \)
となり,タクシーの式は,
\( y=10x-100 \) となります。
自転車の式は,\( y=\dfrac{25}{4}x \) なので,
連立方程式として解くと,
タクシーが自転車に追いつく時間は,
連立方程式の解として求めることができます。
\( \left\{ \begin{array}{}
y=10x-100 \;\; ・・・ \;\; ➀ \\
y=\dfrac{25}{4}x \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
\( 10x-100=\dfrac{25}{4}x \)
\( 15x=400 \)
\( x=\dfrac{80}{3} \)
よって,タクシーが自転車に追いつく時間は,\( \dfrac{80}{3} \) 秒後
バスが自転車に追いつく時間は,\( 25 \) 秒後なので,バスより先に追いつくことはできない。
大問5
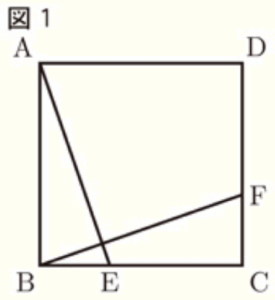
正方形 \( ABCD \) で,辺 \( BC,CD \) 上に,点 \( E,F \) を,\( BE=CF \) となるようにそれぞれとる。
このとき,\( AE=BF \) であることを,図1をかいて,\( △ABE≡△BCF \) を示すことで証明した。
証明
\( △ABE \) と \( △BCF \) において
仮定から,\( BE=CF \) ・・・ ➀
四角形 \( ABCD \) は正方形だから
\( AB=BC \) ・・・ ➁
\( ∠ABE=∠BCF=90° \) ・・・ ➂
➀,➁,➂より, がそれぞれ等しいので
\( △ABE≡△BCF \)
合同な図形では,対応する線分の長さはそれぞれ等しいから
\( AE=BF \)
次の (1)~(4) に答えよ。
(1) にあてはまる言葉をかき,上の証明を完成させよ。
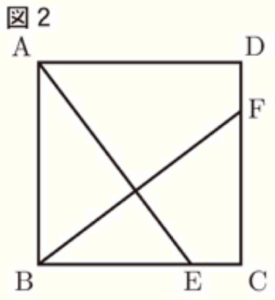
(2) 上の証明をしたあと,辺 \( BC,CD \) 上に,点 \( E,F \) を,図1の位置とは異なる位置に,\( BE=CF \) となるようにそれぞれとり,図2をかいた。
図2においても,図1と同じように \( AE=BF \) である。
このことの証明について,正しいことを述べているものを,次のア~エから1つ選び,記号をかけ。
ア 上の証明をしても,あらためて証明しなおす必要がある。
イ 上の証明で,すでに示されているので,証明しなおす必要はない。
ウ 上の証明の一部をかきなおして,証明しなければならない。
エ 上の証明をしても,線分AEと線分BFの長さを測って確認しなければならない。
【解説】
「辺 \( BC,CD \) 上に,点 \( E,F \) を,\( BE=CF \) となるようにそれぞれとる。」
となっているので,
「辺 \( BC,CD \) 上に」・「\( BE=CF \) となるように」点 \( E,F \) をとっている限りは,
どこに点をとっても証明しなおす必要はありません 。
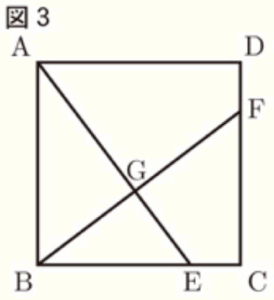
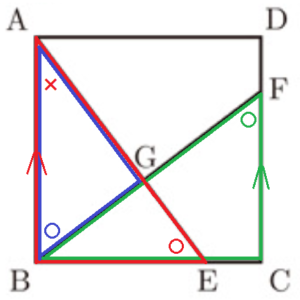
(3) 図3は,図2において,線分 \( AE \) と線分 \( BF \) との交点を \( G \) としたものである。
図3において,\( △ABE \) ∽ \( △AGB \) であることを証明せよ。
ただし, \( △ABE≡△BCF \) であることは使ってよい。
【解答】
\( △ABE \) と \( △AGB \) において,
\( △ABE≡△BCF \) より,
\( ∠AEB=∠BFC \) ・・・ ➀
\( AB//CD \) なので,錯角は等しく,
\( ∠ABG=∠BFC \) ・・・ ➁
➀➁より,\( ∠AEB=∠ABG \) ・・・ ➂
また,\( ∠A \) は共通 ・・・ ④
➂➃より,2組の角がそれぞれ等しいので,
\( △ABE \) ∽ \( △AGB \)
(4) 図3において,\( BE:EC=3:1 \) のとき,四角形 \( GECF \) の面積は,正方形 \( ABCD \) の面積の何倍か求めよ。
【解答】
\( \dfrac{6}{25} \) 倍
【解説】
四角形 \( GECF \) の面積を直接求めるのは難しいので,
四角形 \( GECF=△BCF-△BEG \) となっていること,\( △ABE≡△BCF \),\( △ABE \) ∽ \( △AGB \),であることを使って求めていきます。
\( BE:EC=3:1 \) より,\( BE:BC=3:4 \)
\( AB=BC \) より,\( BE:AB=3:4 \)
\( △ABE \) は \( BE:AB=3:4 \) の直角三角形なので,\( AB:AE=4:5 \)
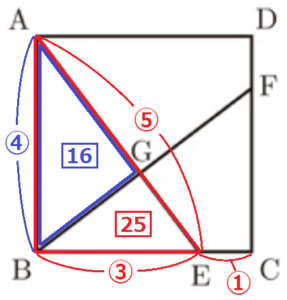
(3) より,\( △ABE \) ∽ \( △AGB \) なので,相似比は \( 5:4 \)
相似な三角形の面積比は相似比の2乗の比と等しいので,
\( △ABE:△AGB=5^2:4^2=25:16 \)
\( △ABE=△AGB+△BGE \) なので,
\( △ABE:△BGE=25:(25-16)=25:9 \)
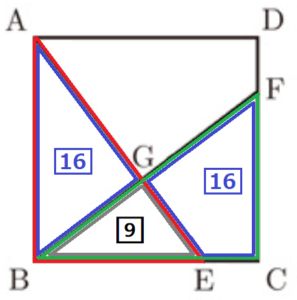
\( △ABE≡△BCF \) より,
\( △BCF:△BGE=25:9 \)
四角形 \( GECF=△BCF-△BEG \) なので,
\( △BCF:\) 四角形 \( GECF=25:(25-9)=25:16 \)
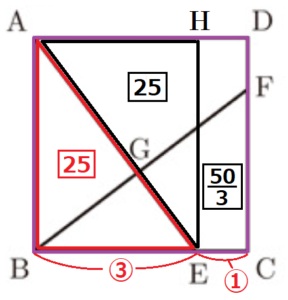
点 \( E \) から辺 \( AD \) に垂線をひき,交点を \( H \) とすると,
四角形 \( ABEH \) は長方形で,線分 \( AE \) は対角線なので,
\( △ABE:\) 四角形 \( ABEH=1:2=25:50 \)
\( BE:EC=3:1 \) より,四角形 \( ABEH: \) 四角形 \( DHEC=3:1 \) なので,
四角形 \( ABEH: \) 四角形 \( DHEC=3:1 \)
\( 25+25: \) 四角形 \( DHEC=3:1 \)
\( 3 \times \) 四角形 \( DHEC=50 \)
四角形 \( DHEC=\dfrac{50}{3} \)
正方形 \( ABCD= \) 四角形 \( ABEH+ \) 四角形 \( DHEC \)
\( =50+\dfrac{50}{3} \)
\( =\dfrac{200}{3} \)
よって,
四角形 \( GECF: \) 正方形 \( ABCD=16: \dfrac{200}{3}\)
\( =48: 200 \)
\( =6: 25 \)
なので,四角形 \( GECF \) の面積は,正方形 \( ABCD \) の面積の \( \dfrac{6}{25} \) 倍
大問6
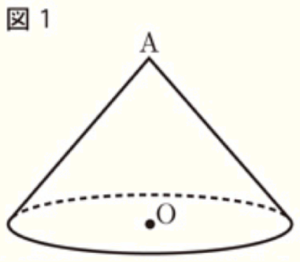
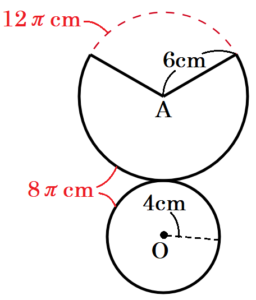
図1は, 半径 \( 4 \; cm \) の円 \( O \) を底面とし,母線の長さが \( 6 \; cm \) の
円すいを表しており,円すいの頂点を \( A \) としたものである。
次の (1)~(3) に答えよ。答えに円周率を使う場合は,\( \pi{} \) で表すこと。
(1) 図1に示す円すいの表面積を求めよ。
【解答】
\( 40\pi{} \; cm^2 \)
【解説】
この円すいを展開すると,半径 \( 6 \; cm \) のおうぎ形と
半径 \( 4 \; cm \) の円になるので,
\( \pi{} \times 6^2 \times \dfrac{8\pi{}}{12\pi{}}+\pi{} \times 4^2=40\pi{} \; (cm^2) \)
(2) 図1に示す円すいと底面が合同で,高さが等しい円柱の容器に,高さを4等分した目盛りがついている。この容器の底面を水平にして,水を入れる。
このとき,図1に示す円すいの体積と同じ量の水を入れた容器を表したものが,次のア~エに1つある。それを選び,記号をかけ。また,選んだ容器の底から水面までの高さを求めよ。
ただし,容器の厚さは考えないものとする。
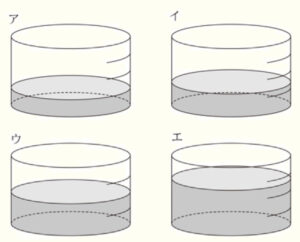
【解答】
イ 高さ \( \dfrac{2\sqrt{5}}{3} \; cm \)
【解説】
円すいと円柱の体積は,
円すい \( = \) 底面積 \( \times \) 高さ \( \times \dfrac{1}{3} \)
円柱 \( = \) 底面積 \( \times \) 高さ
で求められるので,
円すいと円柱の底面が合同(面積が等しい)で,高さが等しいとき,
円すいの体積は,円柱の体積の \( \dfrac{1}{3} \) になります。
よって,容器の \( \dfrac{1}{3} \) だけ水が入っている イ になります。
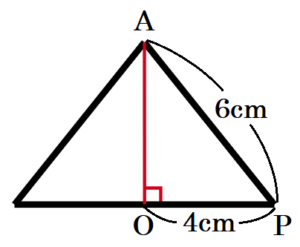
また,円すいを正面から見たとき,
母線と底面の円の半径の交点を点 \( P \) とします。
\( △AOP \) は,\( AP=6 \; cm,OP=4 \; cm \) の直角三角形なので,
三平方の定理より,高さは,
\( AO^2=AP^2+OP^2 \)
\( =6^2+4^2 \)
\( =20 \)
\( AO=2\sqrt{5} \; (cm) \) ( \( AO>0 \)より )
容器は高さが等しく,水は \( \dfrac{1}{3} \) の高さまで入っているので,
水面までの高さは,\( \dfrac{2\sqrt{5}}{3} \; cm \)
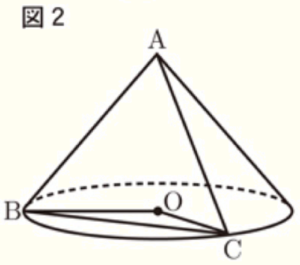
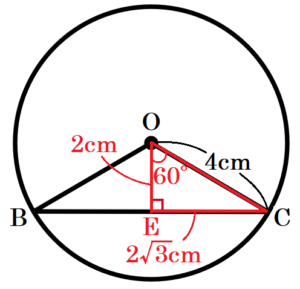
(3) 図2は,図1に示す円すいにおいて,円 \( O \) の円周上に点 \( B,C \) を,\( ∠BOC=120° \) となるようにとり,\( △ABC \) をつくったものである。
図2に示す円すいにおいて,線分 \( BC \) 上に点 \( D \) を,\( AD=CD \) となるようにとるとき,線分 \( OD \) の長さを求めよ。
【解答】
\( \sqrt{7} \; cm \)
【解説】
点 \( O \) から線分 \( BC \) に垂線をひき,交点を点 \( E \) とすると,
\( △OBE≡△OCE \) になっています。
\( ∠BOC=120° \) より,\( ∠COE=\dfrac{1}{2}∠BOC=60° \) なので,
\( △OCE \) は,\( 30°,60°,90° \) の直角三角形であり,
\( OE=\dfrac{1}{2}OC=2 \; (cm) \)
\( CE=\dfrac{\sqrt{3}}{2}OC=2\sqrt{3} \; (cm) \)
となります。
次に,\( △ABC \) に注目すると,線分 \( AB,AC \) は母線になるので。\( AB=AC=6 \; cm \) の二等辺三角形になっています。
ここで,点 \( E \) は線分 \( BC \) の中点なので,\( AE⊥BC \) です。
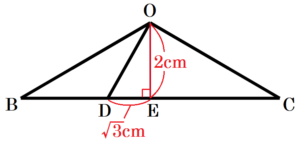
ここで,\( DE=x \; cm \) とすると,\( AD=CD \) より,
\( AD=2\sqrt{3}+x \; cm \) と表すことができるので,
\( △ADE \) と \( △ACE \) において,三平方の定理より,
\( AD^2-DE^2=AC^2-CE^2 \)
\( (2\sqrt{3}+x)^2-x^2=6^2-(2\sqrt{3})^2 \)
\( 4\sqrt{3}x+12=24 \)
\( x=\sqrt{3} \; (cm) \)
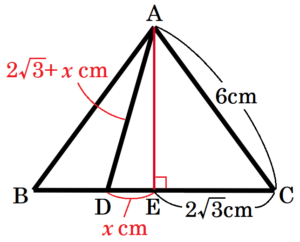
点Dの場所の決め方
三平方の定理より,
\( AE^2=AC^2-CE^2 \)
\( =6^2-(2\sqrt{3})^2 \)
\( =24 \)
\( AE=2\sqrt{6} \; (cm) \)
\( AE>CE \) より,点 \( D \) は \( BE \) 間にあるとわかります。
\( △OBC \) に戻ると,中にできる \( △ODE \) は,
\( OE=2 \; cm,DE=\sqrt{3} \; cm \) の直角三角形なので,
三平方の定理より,
\( OD^2=OE^2+DE^2 \)
\( =2^2+\sqrt{3}^2 \)
\( =7 \)
\( OD=\sqrt{7} \; (cm) \) ( \( OD>0 \)より )