大問1
(1) \( 6-(-4) \div 2 \) を計算した結果として正しいものを,次のアからエまでの中から一つ選びなさい。
ア \( 1 \) イ \( 4 \) ウ \( 5 \) エ \( 8 \)
(2) \( \dfrac{3x-2}{6}-\dfrac{2x-3}{9} \) を計算した結果として正しいものを,次のアからエまでの中から一つ選び
なさい。
ア \( \dfrac{5x-12}{18} \) イ \( \dfrac{13x-12}{18} \) ウ \( \dfrac{5}{18}x \) エ \( -\dfrac{2}{3} \)
【解答】
ウ \( \dfrac{5}{18}x \)
【解説】
\( \dfrac{3x-2}{6}-\dfrac{2x-3}{9}=\dfrac{3(3x-2)-2(2x-3)}{18} \)
\( =\dfrac{9x-6-4x+6}{18} \)
\( =\dfrac{5x}{18} \)
(3) \( 6x^2 \div (-3xy)^2 \times 27xy^2 \) を計算した結果として正しいものを,次のアからエまでの中から
一つ選びなさい。
ア \( -54x^2y \) イ \( -18xy \) ウ \( 18x \) エ \( 54x^2y^2 \)
【解説】
\( 6x^2 \div (-3xy)^2 \times 27xy^2=\dfrac{6x^2 \times 27xy^2}{(-3xy)^2} \)
\( =\dfrac{6x^2 \times 27xy^2}{9x^2y^2} \)
\( =18x \)
(4) \( (\sqrt{5}-\sqrt{2})( \sqrt{20}+\sqrt{8}) \) を計算した結果として正しいものを,次のアからエまでの中から一つ
選びなさい。
ア \( 6 \) イ \( 4\sqrt{5} \) ウ \( 2\sqrt{21} \) エ \( 14 \)
【解説】
\( (\sqrt{5}-\sqrt{2})(\sqrt{20}+\sqrt{8})=(\sqrt{5}-\sqrt{2})(2\sqrt{5}+2\sqrt{2}) \)
\( =2(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2}) \)
\( =2(5-2) \)
\( =2 \times 3 \)
\( =6 \)
(5) 方程式 \( (x-3)^2=-x+15 \) の解として正しいものを,次のアからエまでの中から一つ選びなさい。
ア \( x=-6,1 \) イ \( x=-3,-2 \) ウ \( x=-1,6 \) エ \( x=2,3 \)
【解説】
\( x^2-6x+9=-x+15 \)
\( x^2-5x-6=0 \)
\( (x+1)(x-6)=0 \)
\( x=-1,6 \)
(6) 次のアからエまでの中から,\( y \) が \( x \) の一次関数となるものを一つ選びなさい。
ア 面積が \( 100 \; cm^2 \) で、たての長さが \( x \; cm \) である長方形の横の長さ \( y \; cm \)
イ 1辺の長さが \( x \; cm \) である正三角形の周の長さ \( y \; cm \)
ウ 半径が \( x \; cm \) である円の面積 \( y \; cm^2 \)
エ 1辺の長さが \( x \; cm \) である立方体の体積 \( y \; cm^3 \)
【解説】
\( y \) が \( x \) の一次関数であるとき,\( x \) と \( y \) の関係式は \( y=ax+b \) の形になります。
アからエについて \( x \) と \( y \) の関係式は次のようになります。
ア \( xy=100 \; cm^2 \) ⇒ \( y=\dfrac{100}{x} \) (反比例の式)
イ \( y=3x \)
ウ \( y=\pi{}x^2 \) (二次関数の式)
エ \( y=x^3 \) (三次関数の式)
(7) \( 1 \) が書かれているカードが2枚,\( 2 \) が書かれているカードが1枚,\( 3 \) が書かれているカードが1枚
入っている箱から,1枚ずつ続けて3枚のカードを取り出す。
1枚目を百の位,2枚目を十の位,3枚目を一の位として,3けたの整数をつくるとき,この
整数が \( 213 \) 以上となる確率として正しいものを,次のアからエまでの中から一つ選びなさい。
ア \( \dfrac{7}{24} \) イ \( \dfrac{1}{3} \) ウ \( \dfrac{5}{12} \) エ \( \dfrac{1}{2} \)
【解答】
ウ \( \dfrac{5}{12} \)
【解説】
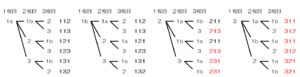
\( 1 \) が書かれているカード2枚に \( 1a,1b \) と名前をつけて選んだカードの組み合わせと
それによりできる整数を樹形図に書いてみます。
できた整数が \( 213 \) 以上となる組み合わせは10通り,すべての組み合わせは24通りなので,
求める確率は \( \dfrac{10}{24}=\dfrac{5}{12} \)
(8) \( n \) がどんな整数であっても,式の値が必ず奇数となるものを,次のアからエまでの中から一つ選び
なさい。
ア \( n-2 \) イ \( 4n+5 \) ウ \( 3n \) エ \( n^2-1 \)
【解説】
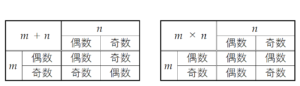
偶数,奇数の和について、
偶数 \( + \) 偶数 \( = \) 偶数,偶数 \( + \) 奇数 \( = \) 奇数,奇数 \( + \) 偶数 \( = \) 奇数,奇数 \( + \) 奇数 \( = \) 偶数
偶数,奇数の積について、
偶数 \( \times \) 偶数 \( = \) 偶数,偶数 \( \times \) 奇数 \( = \) 偶数,奇数 \( \times \) 偶数 \( = \) 偶数,奇数 \( \times \) 奇数 \( = \) 奇数
の関係が成り立ちます
ア \( n \) が偶数のとき,\( n-2 \) は 「偶数 \( + \) 偶数」なので,偶数 (\( -2 \) は偶数)
\( n \) が奇数のとき,\( n-2 \) は 「奇数 \( + \) 偶数」なので,奇数
イ \( n \) が偶数のとき,\( 4n+5 \) は 「偶数 \( \times \) 偶数 \( + \) 奇数」なので,奇数
\( n \) が奇数のとき,\( 4n+5 \) は 「偶数 \( \times \) 奇数 \( + \) 奇数」なので,奇数
ウ \( n \) が偶数のとき,\( 3n \) は 「奇数 \( \times \) 偶数」なので,偶数
\( n \) が奇数のとき,\( 3n \) は 「奇数 \( \times \) 奇数」なので,奇数
エ \( n \) が偶数のとき,\( n^2-1 \) は 「偶数 \( \times \) 偶数 \( + \) 奇数」なので,奇数 (\( -1 \) は奇数)
\( n \) が奇数のとき,\( n^2-1 \) は 「奇数 \( \times \) 奇数 \( + \) 奇数」なので,偶数
別解
整数 \( n \) は,偶数 \( 2m \) と奇数 \( 2m+1 \) (\( m \) は整数)に分けることができます。
アから
エの式に \( n=2m \) と \( n=2m+1 \) を代入したときに
\( 2k \) の形に変形できれば偶数,\( 2k+1 \) の形に変形できれば奇数になります。
つまり,\( n=2m \) と \( n=2m+1 \) を代入したときに,
どちらも \( 2k+1 \) の形に変形できるものを選べばよいことになります。
ア \( n=2m \) のとき,\( 2m-2=2(m-1) \) なので,偶数
\( n=2m+1 \) のとき,\( (2m+1)-2=2(m-1)+1 \) なので,奇数
イ \( n=2m \) のとき,\( 4 \times 2m+5=8m+5=2(4m+2)+1 \) なので,奇数
\( n=2m+1 \) のとき,\( 4 \times (2m+1)+5=8m+9=2(4m+4)+1 \) なので,奇数
ウ \( n=2m \) のとき,\( 3 \times 2m=2 \times 3m \) なので,偶数
\( n=2m+1 \) のとき,\( 3 \times (2m+1)=6m+3=2(3m+1)+1 \) なので,奇数
エ \( n=2m \) のとき,\( (2m)^2-1=4m^2-1=2(2m^2-1)+1 \) なので,奇数
\( n=2m+1 \) のとき,\( (2m+1)^2-1=4m^2+4m=2(2m^2+2m) \) なので,偶数
(9) \( x \) の値が \( 1 \) から \( 3 \) まで増加するときの変化の割合が,関数 \( y=2x^2 \) と同じ関数を,
次のアからエまでの中から一つ選びなさい。
ア \( y=2x+1 \) イ \( y=3x-1 \) ウ \( y=5x-4 \) エ \( y=8x+6 \)
【解説】
\( y=2x^2 \) について,\( x \) の値が \( 1 \) から \( 3 \) まで増加するときの変化の割合は,
\( \dfrac{2 \times 3^2-2 \times 1^2}{3-1}=\dfrac{16}{2}=8 \)
よって,変化の割合が等しいのは エ になります。
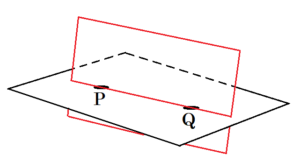
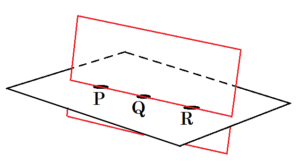
(10) 空間内の平面について正しく述べたものを,次のアからエまでの中から全て選びなさい。
ア 異なる2点をふくむ平面は1つしかない。
イ 交わる2直線をふくむ平面は1つしかない。
ウ 平行な2直線をふくむ平面は1つしかない。
エ 同じ線上にある3点をふくむ平面は1つしかない。
【解説】
直線1本に対しては,無限に平面をとることができます。
異なる2直線が同一平面にある場合は,その面以外の平面をとることはできません。
ア 異なる2点を通る直線は1本しかないので,平面は無限にとることができます。
反例
エ 3点が同じ線上にある場合も直線は1本しかないので,平面は無限にとることができます。
反例
大問2
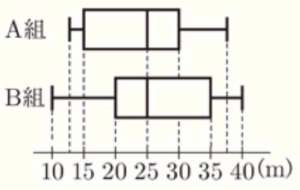
(1) 図は,ある中学校のA組32人とB組32人のハンドボール投げの記録を,箱ひげ図で表したものである。
この箱ひげ図から分かることについて,正しく述べたものを次のアからオまでの中から二つ選びなさい。
ア A組とB組は、範囲がともに同じ値である。
イ A組とB組は、 四分位範囲がともに同じ値である。
ウ A組とB組は、中央値がともに同じ値である。
エ \( 35 \; m \) 以上の記録を出した人数はB組よりA組の方が多い。
オ \( 25 \; m \) 以上の記録を出した人数は,A組,B組ともに同じである。
【解説】
ア 箱ひげ図で範囲は下の図のところです。
問題の箱ひげ図では,明らかにA組の範囲の方が小さくなっています。
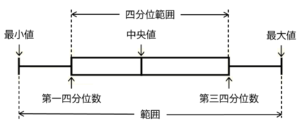
イ 四分位範囲は「第三四分位数 \( – \) 第一四分位数」で求められます。
A組 ・・・ \( 30-15=15 \; (m) \)
B組 ・・・ \( 35-20=15 \; (m) \)
ウ A組とB組は、中央値がともに同じ値である。
中央値は,A組とB組どちらも \( 25 \; m \) になっています。
エ \( 35 \; m \) 以上の記録を出した人数は,
B組:第三四分位数が \( 35 \; m \) なので,8人以上います。
A組:第三四分位数が \( 30 \; m \) なので,8人以上になります。
よって,A組の人数は,B組と同じまたはB組より少なくなっています。
オ A組,B組とも全部で32人ずつなので,
中央値は記録の小さい方から16番目の人と17番目の人の記録の平均値になります。
例えば,A組の16番目,17番目の人の記録がともに \( 25 \; m \) だとすると,
中央値は \( 25 \; m \) ですし,
B組の16番目の人の記録が \( 24 \; m \),17番目の人の記録が \( 26 \; m \) だとしても,
中央値は \( 25 \; m \) になります。
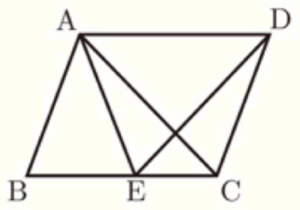
(2) 図で,四角形 \( ABCD \) は平行四辺形であり,\( E \) は \( BC \) 上の点で,\( AB=AE \) である。
このとき \( △ABC \) と \( △EAD \) が合同であることを,次のようにしたい。
( Ⅰ ),( Ⅱ )にあてはまる最も適当なものを,下のアからコまでの中からそれぞれ選びなさい。
なお,2か所の( Ⅰ ),( Ⅱ )には、それぞれ同じものがあてはまる。
(証明)
\( △ABC \) と \( △EAD \) で,
仮定より, \( AB=EA \) ・・・ ➀
平行四辺形の向かい合う辺は等しいから, \( BC=AD \) ・・・ ➁
二等辺三角形の底角は等しいから, \( ∠ABC= \)( Ⅰ ) ・・・ ➂
平行線の錯角は等しいから, ( Ⅰ )\( = \)( Ⅱ ) ・・・ ➃
➂,➃より, \( ∠ABC= \)( Ⅱ ) ・・・ ➄
➀,➁,➄ から2組の辺とその間の角がそれぞれ等しいから,
\( △ABC≡△EAD \)
ア \( ∠ACD \) イ \( ∠ACE \) ウ \( ∠ADC \) エ \( ∠ADE \) オ \( ∠AEB \)
カ \( ∠AEC \) キ \( ∠EAC \) ク \( ∠EAD \) ケ \( ∠ECD \) コ \( ∠EDC \)
【解答】
( Ⅰ )・・・ オ
( Ⅱ )・・・ ク
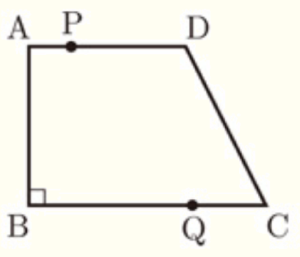
(3) 図で,四角形 \( ABCD \) は \( AD//BC, ∠ABC=90° \),
\( AD=4 \; cm, BC=6 \; cm \) の台形である。点 \( P,Q \) はそれぞれ頂点 \( A,C \) を同時に出発し,点 \( P \) は毎秒 \( 1 \; cm \) の速さで辺 \( AD \) 上を,点 \( Q \) は毎秒 \( 2 \; cm \) の速さで辺 \( CB \) 上をくり返し往復する。
点 \( P \) が頂点 \( A \) を出発してから \( x \) 秒後の \( AP \) の長さを \( y \; cm \) とするとき,次の ➀,➁ の問いに答えなさい。
ただし,点 \( P \) が頂点 \( A \) と一致するときは \( y=0 \) とする。
なお,下の図を必要に応じて使ってもよい。
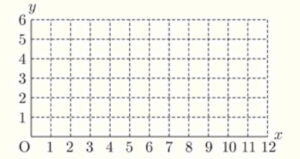
➀ \( x=6 \) のときの \( y \) の値として正しいものを,次のアからオまでの中から一つ選びなさい。
ア \( y=0 \) イ \( y=1 \) ウ \( y=2 \) エ \( y=3 \) オ \( y=4 \)
【解説】
点 \( P \) は毎秒 \( 1 \; cm \) の速さで辺 \( AD \) 上を動くので,
\( 4 \) 秒かけて \( A \) から \( D \) まで移動し,
さらに,\( 2 \) 秒かけて \( 2 \; cm \) だけ \( A \) に向けて戻ってくるので,
\( 6 \) 秒後の \( AP \) の長さは \( 4-2=2 \; (cm) \) になります。
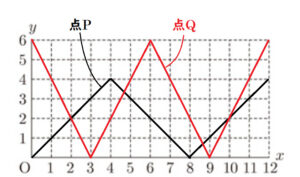
➁ 点 \( P,Q \) が頂点 \( A,C \) を同時に出発してから \( 12 \) 秒後までに,\( AB//PQ \) となるときは何回あるか,次のアからオまでの中から一つ選びなさい。
ア 1回 イ 2回 ウ 3回 エ 4回
【解説】
点 \( P \) の場合と同じように
点 \( Q \) が頂点 \( C \) を出発してから \( x \) 秒後の \( BQ \) の長さを \( y \; cm \) として,
\( AP,BQ \) の長さの関係を表す直線をそれぞれ書き込みます。
\( AB//PQ \) となるのは,\( AP=BQ \) となるとき,
つまり,2本の直線の \( y \) の値が等しくなるときなので,
グラフ中では2本の直線の交点になります。
よって,\( AB//PQ \) となるのは4回になります。
大問3
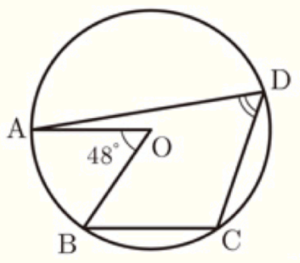
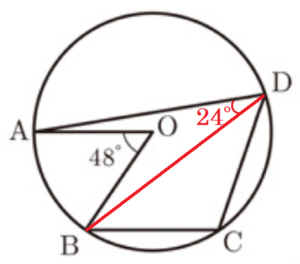
(1) 図で,\( A,B,C,D \) は円 \( O \) の周上の点で,\( AO//BC \) である。
\( ∠AOB=48° \) のとき,\( ∠ADC \) の大きさは 度である。
【解説】
\( ∠ADC \) を線分 \( BD \) で2つに分けると,
\( ∠AOB \) は弧 \( AB \) の中心角,\( ∠ADB \) は弧 \( AB \) の円周角なので,
\( ∠ADB=\dfrac{1}{2}∠AOB=24° \)
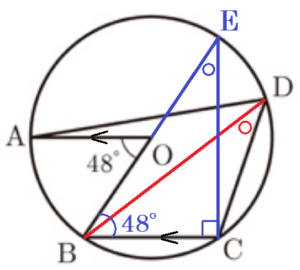
線分 \( BO \) を延長したときの円 \( O \) との交点を点 \( E \) とすると,線分 \( BE \) は直径になるので,\( ∠BCE=90° \)
また,\( AO//BC \) より,錯角は等しいので,\( ∠CBE=∠AOB=48° \)
ここから,\( ∠BEC=180°-(∠BCE+∠CBE)=42° \)
\( ∠BDC \) と \( ∠BEC \) はともに弧 \( AB \) の円周角なので,
\( ∠BDC=∠BEC=42° \)
よって,\( ∠ADC=∠ADB+∠BDC=66° \)
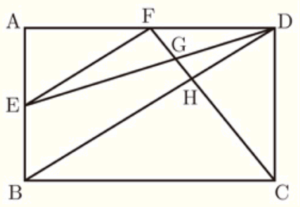
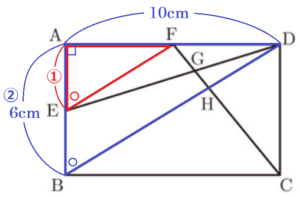
(2) 図で,四角形 \( ABCD \) は長方形で,\( E \) は辺 \( AB \) の中点である。また,\( F \) は辺 \( AD \) 上の点で,\( FE//DB \) であり,\( G,H \) はそれぞれ線分 \( FC \) と \( DE,DB \) との交点である。
\( AB=6 \; cm,AD=10 \; cm \) のとき、
➀ 線分 \( FE \) の長さは, \( cm \) である。
【解説】
\( FE//DB \) より,同位角は等しいので,
\( ∠AEF=∠ABD \)
\( ∠A \) は共通
2組の角がそれぞれ等しいので,
\( △AEF \) ∽ \( △ABD \)
対応する辺の比は等しいので,
\( EF:BD=AE:AB=1:2 \)
\( EF=\dfrac{1}{2}BD \)
\( BD^2=AB^2+AD^2 \)
\( =6^2+10^2 \)
\( =134 \)
\( BD=2\sqrt{34} \; (cm) \)
よって,
\( EF=\dfrac{1}{2} \times 2\sqrt{34}=\sqrt{34} \; (cm) \)
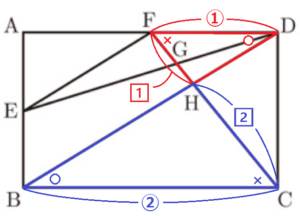
➁ \( △DGH \) の面積は \( cm^2 \) である。
【解説】
\( △DGH \) の面積を直接求めるのは難しいので,
\( △DGH \) と \( △CDF \) の面積比から求めることにします。
\( △DGH \) と \( △CDF \) は底辺をそれぞれ \( GH,CF \) とすると,高さが共通なので,
\( △DGH:△CDF=GH:CF \) となります。
\( △DFH \) と \( △BCH \) において,
長方形の向かい合う辺は平行なので,\( AD//BC \)
錯角は等しいので,
\( ∠HDF=∠HBC,∠HFD=∠HCB \)
2組の角がそれぞれ等しいので,
\( △DFH \) ∽ \( △BCH \)
問➀より
\( △AEF \) ∽ \( △ABD \),相似比 \( 1:2 \) なので,
\( F \) は \( AD \) の中点であり,
\( FH:CH=DF:BC=1:2 \)
線分 \( DE,BC \) をそれぞれ延長したときの交点を点 \( I \) とすると,
\( △ADE \) と \( △BIE \) において,
長方形のすべての角は \( 90° \) なので,\( ∠DAE=∠IBE \)
対頂角は等しいので,\( ∠AED=∠BEI \)
\( E \) は辺 \( AB \) の中点なので,\( AE=BE \)
1組の辺とその両端の角がそれぞれ等しいので,\( △ADE≡△BIE \)
対応する辺の長さは等しいので,\( AD=BI \)
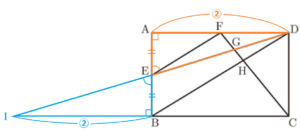
\( △DFG \) と \( △ICG \) において,
錯角は等しいので,
\( ∠GDF=∠GIC,∠GFD=∠GCI \)
2組の角がそれぞれ等しいので,
\( △DFG \) ∽ \( △ICG \)
\( FD:AD=1:2,AD=BC=BI \) より,\( FD:CI=1:4 \)
対応する辺の比は等しいので,\( GF:GC=FD:CI=1:4 \)
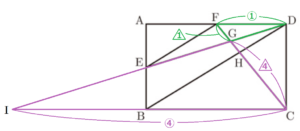
以上より,
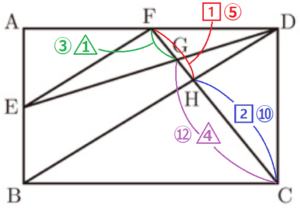
\( FH:CH=1:2=5:10 \)
\( GF:GC=1:4=3:12 \)
であり,
\( FG:GH:HC=3:2:10 \)
\( GH:CF=2:15 \)
問➀で \( △AEF \) ∽ \( △ABD \),相似比 \( 1:2 \) であることがわかっているので,
\( △CDF=DF \times CD \times \dfrac{1}{2} \)
\( =5 \times 6 \times \dfrac{1}{2} \)
\( =15 \; (cm^2) \)
よって,
\( △DGH:△CDF=GH:CF \)
\( △DGH:15=2:15 \)
\( △DGH=2 \; (cm^2) \)
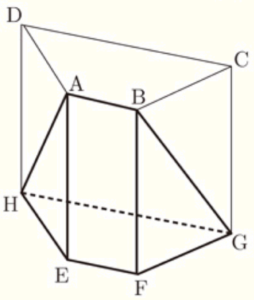
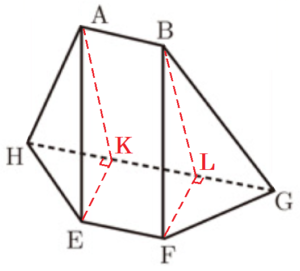
(3) 図で,立体 \( ABCDEFGH \) は底面が台形の四角柱で,\( AB//DC \) である。
\( AB=3 \; cm,AE=7 \; cm,CB=DA=5 \; cm,DC=9 \; cm \) のとき。
➀ 台形 \( ABCD \) の面積は \( cm^2 \) である。
【解説】
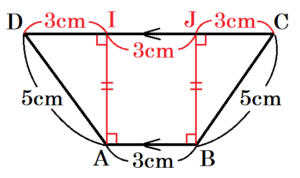
点 \( A,B \) から辺 \( CD \) に垂線をひき,
交点を点 \( I,J \) とすると,
台形 \( ABCD \) は等脚台形なので,\( ID=JC=3 \; cm \)
(詳細は別途解説あります)
\( △AID \) において,三平方の定理より,
\( AI^2=AD^2-ID^2 \)
\( =5^2-3^2 \)
\( =16 \)
\( AI=4 \; (cm) \) ( \( AI>0 \) より)
よって,
台形 \( ABCD=(AB+CD) \times AI \times \dfrac{1}{2} \)
\( =(3+9) \times 4 \times \dfrac{1}{2}=24 \; (cm^2) \)
ID=JC=3cm の求め方
\( △AID \) と \( △BCJ \) において,
仮定より,\( AD=BC=5cm \)
四角形 \( ABJI \) は長方形で,
長方形の向かい合う辺は等しいので,\( AI=BJ \),
\( AI⊥CD,BJ⊥CD \) より,\( ∠AID=∠BIC=90° \)
直角三角形の斜辺と他の1辺の長さが等しいので,
\( △AID≡△BCJ \)
対応する辺の長さは等しいので,\( ID=JC \)
よって,\( ID=\dfrac{CD-IJ}{2}=3 \; (cm) \)
➁ 立体 \( ABEFGH \) の体積は \( cm^3 \) である。
【解説】
点 \( E,F \) から辺 \( GH \) に垂線をひき,交点を点 \( K,L \) とします。
立体 \( ABEFGH \) を面 \( AEK,BFL \) で切断すると,
三角すい \( A-EHK \),三角柱 \( AEK-BFL \),
三角すい \( B-FGL \) の3つに分かれます。
四角形 \( ABCD \) と四角形 \( EFGH \) は合同なので,
問➀より,
\( HK=GL=3 \; cm,EK=FL=4 \; cm \)
であり,
三角すい \( A-EHK \) の体積は,
\( \left( HK \times EK \times \dfrac{1}{2} \right) \times AE \times \dfrac{1}{3} =\left( 3 \times 4 \times \dfrac{1}{2} \right) \times 7 \times \dfrac{1}{3} \)
\( =14 \; (cm^3) \)
三角柱 \( AEK-BFL \) の体積は,
\( \left( AE \times EK \times \dfrac{1}{2} \right) \times AB=\left( 7 \times 4 \times \dfrac{1}{2} \right) \times 3 \)
\( =42 \; (cm^3) \)
三角すい \( B-FGL \) の体積は,
\( \left( GL \times FL \times \dfrac{1}{2} \right) \times BF \times \dfrac{1}{3} =\left( 3 \times 4 \times \dfrac{1}{2} \right) \times 7 \times \dfrac{1}{3} \)
\( =14 \; (cm^3) \)
よって,
立体 \( ABEFGH= \) 三角すい \( A-EHK+ \) 三角柱 \( AEK-BFL+ \) 三角すい \( B-FGL \)
\( =14+42+14 \)
\( =70 \; (cm^3) \)