大問1
(1) \( 3+8 \div (-4) \) を計算せよ。
【解説】
\( =3+(-2) \)
\( =1 \)
(2) \( 6×\dfrac{5}{3}-5^2 \) を計算せよ。
【解説】
\( =10-25 \)
\( =-15 \)
(3) \( \dfrac{x+2y}{2}+\dfrac{4x-y}{6} \) を計算せよ。
【解答】
\( \dfrac{7x+5y}{6} \)
【解説】
\( =\dfrac{3(x+2y)}{6}+\dfrac{4x-y}{6} \)
\( =\dfrac{3x+6y+4x-y}{6} \)
\( =\dfrac{7x+5y}{6} \)
(4) \( \sqrt{8}-\sqrt{3}(\sqrt{6}-\sqrt{27}) \) を計算せよ。
【解説】
\( =\sqrt{8}-\sqrt{3}(\sqrt{6}-\sqrt{27}) \)
\( =2\sqrt{2}-\sqrt{3}(\sqrt{6}-3\sqrt{3}) \)
\( =2\sqrt{2}-\sqrt{18}+9 \)
\( =2\sqrt{2}-3\sqrt{2}+9 \)
\( =9-\sqrt{2} \)
(5) \( (x+1)(x-3)+4 \) を因数分解せよ。
【解説】
\( =x^2-2x-3+4 \)
\( =x^2-2x+1 \)
\( =(x-1)^2 \)
(6) \( x \) についての2次方程式 \( -x²+ax+21=0 \) の解の1つが \( 3 \) のとき,\( a \) の値を求めよ。
【解説】
\( -x²+ax+21=0 \) に \( x=3 \) を代入すると,
\( -3²+3a+21=0 \)
\( 3a+12=0 \)
\( a=-4 \)
(7) 次のア~エの数のうち,12の倍数であるものはどれか。正しいものを1つ選んで,その記号を書け。
ア \( 2 \times 3^4 \) イ \( 2 \times 3^2 \times 7 \) ウ \( 2^2 \times 3^2 \times 5 \) エ \( 2^3 \times 5 \times 7 \)
【解説】
ア~エは,何かの整数を素因数分解した形で表されています。
\( 12 \) を素因数分解すると,\( 2^2 \times 3 \) なので,
ア~エのうち,\( 2 \) を2個,\( 3 \) を1個含むものが12の倍数になります。
よって,あてはまるのは,ウ
大問2
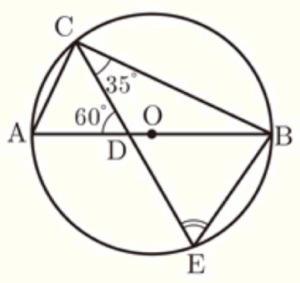
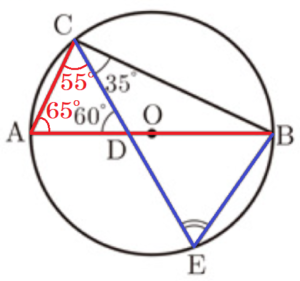
(1) 右の図のような,線分 \( AB \) を直径とする円 \( O \) があり,円周上に2点 \( A,B \) と異なる点 \( C \) をとる。線分 \( AB \) 上に,2点 \( A,B \) と異なる点 \( D \) をとる。2点 \( C,D \) を通る直線と円 \( O \) との交点のうち,点 \( C \) と異なる点を \( E \) とする。点 \( A \) と点 \( C \),点 \( B \) と点 \( E \) をそれぞれ結ぶ。
\( ∠BCE=35°,∠ADC=60° \) であるとき,\( ∠BEC \) の大きさは何度か。
【解説】
\( ∠ACB \) は直径 \( AB \) の円周角なので,\( ∠ACB=90° \)
\( ∠ACD=∠ACB-∠BCD=55° \)
\( ∠CAD=180°-(∠ACD+∠ADC)=65° \)
弧 \( BC \) の円周角なので,\( ∠BEC=∠CAD=65° \)
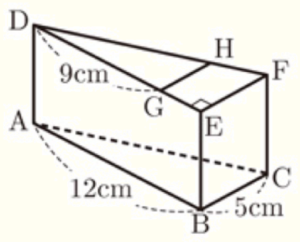
(2) 右の図のような三角柱がある。辺 \( DE \) 上に2点 \( D,E \) と異なる点 \( G \) をとり,点 \( G \) を通り,辺 \( EF \) に平行な直線と,辺 \( DF \) との交点を \( H \) とする。
\( AB=12 \; cm,BC=5 \; cm,DG=9 \; cm,∠DEF=90° \) で,この三角柱の表面積が \( 240 \; cm^2 \) であるとき,次のア,イの問いに答えよ。
ア 線分 \( GH \) の長さは何 \( cm \) か。
【解答】
\( \dfrac{15}{4} \; cm \)
【解説】
三角柱の2つの底面(上面と下面)は合同になるので,
\( DE=AB=12 \; cm,EF=BC=5 \; cm \) になっています。
\( EF//GH \) より,\( ∠DGH=∠DEF \) なので,
\( ∠DGH=∠DEF \),\( ∠D \)共通 より,\( △DGH \) ∽ \( △DEF \)
よって,
\( DG:DE=GH:EF \)
\( 9:12=GH:5 \)
\( 12GH=45 \)
\( GH=\dfrac{15}{4} \; (cm) \)
イ この三角柱の体積は何 \( cm^3 \) か。
【解説】
三角柱の2つの底面(上面と下面)の面積は,
\( 12 \times 5 \times \dfrac{1}{2}=30 \; (cm^2) \)
なので,側面にあたる3つの面の面積の合計は,
\( 240-30 \times 2=180 \; (cm^2) \)
\( △ABC \) において,三平方の定理より,
\( AC^2=12^2+5^2=169 \; (cm^2) \)
\( AC=13 \; (cm) \) (\( AC>0 \)より)
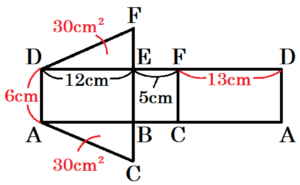
この三角柱の展開図を考えると,側面にあたる3つの面は,右図のように長方形になります。
このとき,
\( DD=DE+EF+FD=30 \; (cm) \),
面積は \( 180 \; cm^2 \) なので,
\( AD=\dfrac{180}{30}=6 \; (cm) \)
よって,三角柱の体積は,
\( △ABC \times AD=30 \times 6=180 \; (cm^3) \)
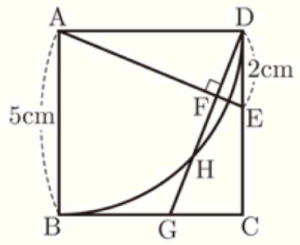
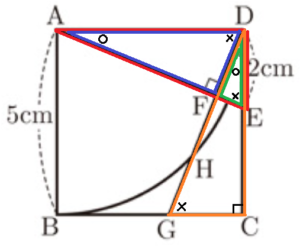
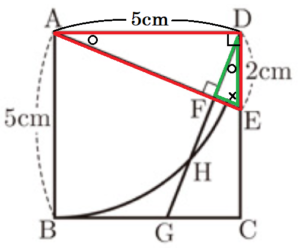
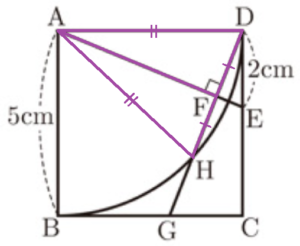
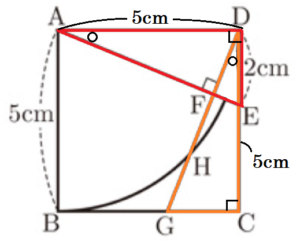
(3) 右の図のような,正方形 \( ABCD \) がある。辺 \( CD \) 上に,2点 \( C,D \) と異なる点 \( E \) をとり,点 \( A \) と点 \( E \) を結ぶ。点 \( D \) から線分 \( AE \) に垂線をひき,その交点を \( F \) とし,直線 \( DF \) と辺 \( BC \) との交点を \( G \) とする。点 \( A \) を中心 として,半径 \( AB \) の円をかき,線分 \( DG \) との交点のうち,点 \( D \) と異なる点を \( H \) とする。
\( AB=5 \; cm,DE=2 \; cm \) であるとき,線分 \( GH \) の長さは何 \( cm \) か。
【解答】
\( \dfrac{9\sqrt{29}}{29} \; cm \)
【解説】
\( △ADE \) において,\( ∠DAE=○,∠AED=× \) とすると,
3つの角が \( ○,×,90° \) になっており,
\( ○+×+90°=180° \)
\( ○+×=90° \)
ここから,\( △AFD,△DFE,△DCG \) も
3つの角が \( ○,×,90° \) になっており,
これら4つの三角形はすべて相似になっています。
\( △ADE \) において,\( AD=AB=5 \; cm,DE=2 \; cm \) なので,三平方の定理より,
\( AE^2=5^2+2^2=29 \; (cm^2) \)
\( AE=\sqrt{29} \; (cm) \) (\( AE>0 \)より)
\( △ADE \) ∽ \( △DFE \) より,
\( AD:DF=AE:DE \)
\( 5:DF=\sqrt{29}:2 \)
\( DF=\dfrac{10}{\sqrt{29}}=\dfrac{10\sqrt{29}}{29} \; (cm) \)
\( △ADH \) は \( AD=AH \) の二等辺三角形で,
頂角から底辺に垂線をひいたとき,底辺を2等分するので,
\( FH=DF=\dfrac{10\sqrt{29}}{29} \; (cm) \)
よって,
\( DH=DF+FH \)
\( =\dfrac{10\sqrt{29}}{29}+\dfrac{10\sqrt{29}}{29} \)
\( =\dfrac{20\sqrt{29}}{29} \; (cm) \)
\( △ADE \) と \( △DCG \) において,
\( AD=DC,∠ADE=∠DCG,∠DAE=∠CDG \) より,
1組の辺とその両端の角がそれぞれ等しいので,
\( △ADE≡△DCG \)
対応する辺の長さは等しいので,\( DG=AE=\sqrt{29} \; (cm) \)
以上より,
\( GH=DG-DH=\dfrac{9\sqrt{29}}{29} \; (cm) \)
大問3
(1) \( y \) は \( x \) に反比例し,\( x=2 \) のとき \( y=5 \) である。\( x=3 \) のときの \( y \) の値を求めよ。
【解答】
\( y=\dfrac{10}{3} \)
【解説】
反比例を表す式は \( y=\dfrac{a}{x} \) になります。
ここに \( x=2,y=5 \) を代入すると,
\( 5=\dfrac{a}{2} \)
\( a=10 \)
となり,もとの式は \( y=\dfrac{10}{x} \) になります。
ここに \( x=3 \) を代入すると,
\( y=\dfrac{10}{3} \)
(2) 2つのくじA,Bがある。くじAには,5本のうち,2本の当たりが入っている。くじBには,4本のうち,3本の当たりが入っている。くじA,Bからそれぞれ1本ずつくじを引くとき,引いた2本のくじのうち,少なくとも1本は当たりである確率を求めよ。
【解答】
\( \dfrac{17}{20} \)
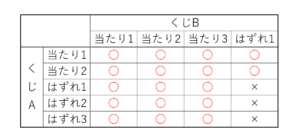
【解説】
くじA,Bから引いたくじの組み合わせを表にして,
当たりが含まれる場合には
○ ,2本ともはずれの場合には
× をつけます。
すべての組み合わせは20通り,2本ともはずれの組み合わせは17通りなので,
確率は \( \dfrac{17}{20} \)
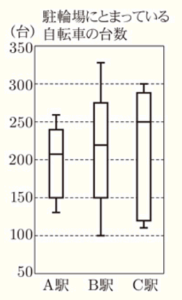
(3) 右の図は,A駅,B駅,C駅それぞれの駐輪場にとまっている自転車の台数を,6月の30日間,毎朝8時に調べ,そのデータを箱ひげ図に表したものである。次のア~エのうち,この箱ひげ図から読みとれることとして,必ず正しいといえることはどれか。2つ選んで,その記号を書け。
ア A駅について,自転車の台数が200台以上であった日数は15日
以上である。
イ A駅とB駅について,自転車の台数が150台未満であった日数を
比べると,B駅の方が多い。
ウ B駅とC駅について,自転車の台数の四分位範囲を比べると,C駅
の方が大きい。
エ A駅,B駅,C駅について,自転車の台数の最大値を比べると,C
駅がもっとも大きい。
【解説】
ア データの総数は30日なので,15日以上が第二四分位数(中央値)以上の値になります。
A駅の第二四分位数(中央値)は200台より大きいので正しい。
イ A駅,B駅ともに第一四分位数が150台になっています。データの総数は30日なので,
少ない方から8番目の値が第一四分位数になります。
よって,150台未満であった日数はA駅,B駅ともに7日以下であることしかわかりません。
ウ 四分位範囲=第三四分位数 \( – \) 第一四分位数 で求められます。
つまり,箱の長さが長いほど四分位範囲は大きくなります。
よって,C駅の方が四分位範囲は大きい。
エ 最大値はB駅がもっとも大きい。
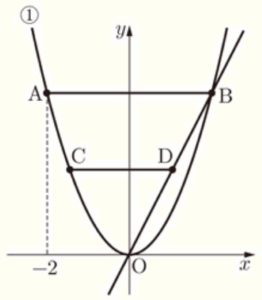
(4) 右の図で,点 \( O \) は原点であり,放物線 ① は関数 \( y=x^2 \) のグラフである。
2点 \( A,B \) は放物線 ① 上の点で,点 \( A \) の \( x \) 座標は \( -2 \) であり,線分 \( AB \) は \( x \) 軸に平行である。点 \( C \) は放物線 ① 上の点で,その \( x \) 座標は負の数である。点 \( C \) を通り,\( x \) 軸に平行な直線をひき,直線 \( OB \) との交点を \( D \) とする。これについて,次のア,イの問いに答えよ。
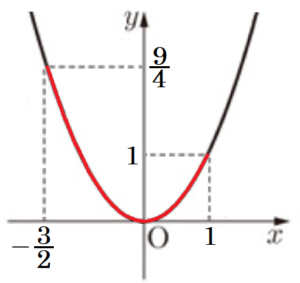
ア 関数 \( y=x^2 \) で,\( x \) の変域が \( -\dfrac{3}{2}≦x≦1 \) のとき,\( y \) の変域を求めよ。
【解答】
\( 0≦y≦\dfrac{9}{4} \)
【解説】
\( y=ax^2 \) \( (a>0) \) のグラフにおいて,
\( x \) の変域が \( 0 \) を含むとき,\( y \) の最小値は必ず \( 0 \) になります。
また,このグラフは \( y \) 軸に対して対称なので,
\( x \) の絶対値が最大になるとき,\( y \) の値も最大になります。
\( -\dfrac{3}{2}≦x≦1 \) の範囲において,\( x \) の絶対値が最大になるのは \( x=-\dfrac{3}{2} \) のときなので,
\( y \) の最大値は,\( y=\left( -\dfrac{3}{2} \right)^2=\dfrac{9}{4} \)
以上より,\( y \) の変域は,\( 0≦y≦\dfrac{9}{4} \)
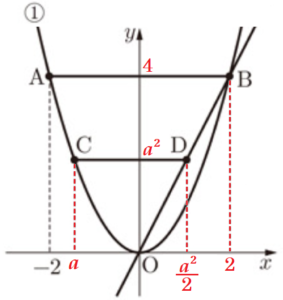
イ \( AB:CD=8:5 \) であるとき,点 \( C \) の \( x \) 座標はいくらか。点 \( C \) の \( x \) 座標を \( a \) として,\( a \) の値を求めよ。\( a \) の値を求める過程も,式と計算を含めて書け。
【解説】
\( y=x^2 \) のグラフは\( y \) 軸に対して対称なので,
線分 \( AB \) は \( x \) 軸に平行,点 \( A \) の \( x \) 座標の値は \( -2 \) から,
点 \( B \) の \( x \) 座標の値は \( 2 \) になります。
点 \( B \) は \( y=x^2 \) 上の点なので,\( y \) 座標の値は\( y=2^2=4 \)
ここから,直線 \( OB \) の式は \( y=2x \)
点 \( C \) は \( y=x^2 \) 上の点なので,\( x \) 座標を \( a \) とするとき,
\( y \) 座標は \( a^2 \) と表すことができます。
線分 \( CD \) は \( x \) 軸に平行なので,
点 \( D \) の \( y \) 座標は点 \( C \) と等しく,\( a^2 \)
点 \( D \) は \( y=2x \) 上の点なので,\( x \) 座標の値は,
\( a^2=2x \)
\( x=\dfrac{a^2}{2} \)
よって,線分 \( CD \) の長さは,\( \dfrac{a^2}{2}-a \)
線分 \( AB \) の長さは,\( 4 \) なので,
\( AB:CD=8:5 \)
\( 4:\left( \dfrac{a^2}{2}-a \right)=8:5 \)
\( 4a^2-8a=20 \)
\( a^2-2a-5=0 \)
\( a=\dfrac{-(-2)±\sqrt{(-2)^2-4 \times 1 \times (-5)}}{2} \)
\( =\dfrac{2±\sqrt{24}}{2} \)
\( =1±\sqrt{6} \)
\( a<0 \)より,\( a=1-\sqrt{6} \)
大問4
(1) 次の会話文を読んで,あとのア,イの問いに答えよ。
先生:ここに何も書かれていないカードがたくさんあります。このカードと何も入っていない袋を使って,次の操作⓵から操作⓹を順におこなってみましょう。
操作⓵ 5枚のカードに自然数を1つずつ書き,その5枚のカードをすべて袋に入れる。
操作⓶ 袋の中から同時に2枚のカードを取り出す。その2枚のカードに書いてある数の和を \( a \) とし,
新しい1枚のカードに \( a \) の値を書いて袋に入れる。取り出した2枚のカードは袋に戻さない。
操作⓷ 袋の中から同時に2枚のカードを取り出す。その2枚のカードに書いてある数の和を \( b \) とし,
新しい1枚のカードに \( b+1 \) の値を書いて袋に入れる。取り出した2枚のカードは袋に戻さない。
操作⓸ 袋の中から同時に2枚のカードを取り出す。その2枚のカードに書いてある数の和を \( c \) とし,
新しい1枚のカードに \( c+2 \) の値を書いて袋に入れる。取り出した2枚のカードは袋に戻さない。
操作⓹ 袋の中から同時に2枚のカードを取り出す。その2枚のカードに書いてある数の和を \( X \) とする。
花子:私は操作⓵で5枚のカード \( \fbox{1},\fbox{2},\fbox{3},\fbox{5},\fbox{7} \) を袋に入れます。次に操作⓶をします。袋の中から \( \fbox{3} \) と \( \fbox{5} \) を取り出したので,\( \fbox{8} \) を袋に入れます。操作⓶を終えて,袋の中のカードは \( \fbox{1},\fbox{2},\fbox{7},\fbox{8} \) の4枚になりました。
太郎:私も操作⓵で5枚のカード \( \fbox{1},\fbox{2},\fbox{3},\fbox{5},\fbox{7} \) を袋に入れました。操作⓶を終えて,袋の中のカードは \( \fbox{3},\fbox{3},\fbox{5},\fbox{7} \) の4枚になりました。次に操作③をします。袋の中から \( \fbox{3} \) と \( \fbox{3} \) を取り出したので,\( \fbox{7} \) を袋に入れます。操作⓷を終えて,袋の中のカードは \( \fbox{5},\fbox{7},\fbox{7} \) の3枚になりました。
花子:操作⓹を終えると,私も太郎さんも \( X= \) P になりました。
先生:2人とも正しく \( X \) の値が求められましたね。
ア 会話文中の P の 内にあてはまる数を求めよ。
【解説】
操作⓵ ・・・ \( \fbox{1},\fbox{2},\fbox{3},\fbox{5},\fbox{7} \)
操作⓶ ・・・ \( \fbox{3} \) と \( \fbox{5} \) を取り出し,\( \fbox{8} \) を袋に入れるので,
袋の中に残るカードは,\( \fbox{1},\fbox{2},\fbox{7},\fbox{8} \)
操作⓷ ・・・ \( \fbox{1} \) と \( \fbox{7} \) を取り出したとすると,\( b+1=1+7+1=9 \) となり,
\( \fbox{9} \) を袋に入れるので,袋の中に残るカードは,\( \fbox{2},\fbox{8},\fbox{9} \)
操作⓸ ・・・ \( \fbox{2} \) と \( \fbox{8} \) を取り出したとすると,\( c+2=2+8+2=12 \) となり,
\( \fbox{12} \) を袋に入れるので,袋の中に残るカードは,\( \fbox{9},\fbox{12} \)
操作⓹ ・・・ \( \fbox{9} \) と \( \fbox{12} \) を取り出すことになるので,\( X=9+12=21 \)
Xの値は5枚のカードを選んだ時点で決定している
操作⓵で \( \fbox{A},\fbox{B},\fbox{C},\fbox{D},\fbox{E} \) の5枚を袋に入れたとします。
操作⓶ ・・・ \( \fbox{A} \) と \( \fbox{B} \) を取り出したとすると,\( \fbox{A+B} \) を袋に入れるので,
袋の中に残るカードは,\( \fbox{C},\fbox{D},\fbox{E},\fbox{A+B} \)
操作⓷ ・・・ \( \fbox{C} \) と \( \fbox{D} \) を取り出したとすると,\( b+1=C+D+1 \) となり,
\( \fbox{C+D+1} \) を袋に入れるので,袋の中に残るカードは,\( \fbox{E},\fbox{A+B},\fbox{C+D+1} \)
操作⓸ ・・・ \( \fbox{A+B} \) と \( \fbox{C+D+1} \) を取り出したとすると,
\( c+2=A+B+C+D+1+2=A+B+C+D+3 \) となり,
\( \fbox{A+B+C+D+3} \) を袋に入れるので,
袋の中に残るカードは,\( \fbox{E},\fbox{A+B+C+D+3} \)
操作⓹ ・・・ \( \fbox{E},\fbox{A+B+C+D+3} \) を取り出すことになるので,\( X=A+B+C+D+E+3 \)
つまり,\( X \) の値は5枚のカードに書かれた数字の和に3を加えた数になります。
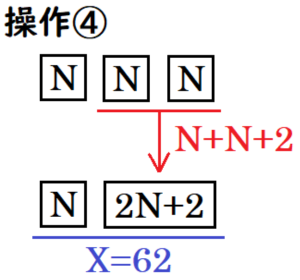
イ 次郎さんも,花子さんや太郎さんのように,操作⓵から操作⓹を順におこなってみることにした。そこで,操作⓵で異なる5つの自然数を書いた5枚のカードを袋に入れた。操作⓶で取り出した2枚のカードの一方に書いてある数は \( 3 \) であった。操作⓷で取り出した2枚のカードの一方に書いてある数は \( 1 \) であり,操作⓷を終えたとき,袋の中にある3枚のカードに書いてある数はすべて同じ数であった。操作⓹を終えると \( X=62 \) になった。このとき,次郎さんが操作⓵で書いた5つの自然数を求めよ。
【解説】
操作⓷を終えたとき,袋の中にある3枚のカードを \( \fbox{N} \) とすると,
操作⓸を終えたとき,袋の中にある2枚のカードは \( \fbox{N},\fbox{2N+2} \) になるので,
\( X=N+2N+2=3N+2 \)
よって,
\( 3N+2=62 \)
\( N=20 \)
操作⓷を終えたとき,袋の中にある \( \fbox{N} \) のうち1枚は \( \fbox{M+2} \) と表すことができるので,
\( M+2=20 \)
\( M=18 \)
ここから,操作⓶を終えたとき,袋の中にある4枚のカードは \( \fbox{1},\fbox{18},\fbox{20},\fbox{20} \)
操作⓵の5枚は異なる数が書かれていたので,
\( \fbox{20} \) のうち1枚は操作⓶で新たに加えられたものだとわかります。
操作⓶で取り出したカードの一方が \( \fbox{3} \) ということは,
もう一方のカードは \( \fbox{17} \) ということになります。
以上より,操作⓵で袋に入れたカードは,\( \fbox{1},\fbox{3},\fbox{17},\fbox{18},\fbox{20} \)
(2) 2日間おこなわれたバザーで,太郎さんのクラスは,ペットボトル飲料,アイスクリーム,ドーナツの3種類の商品を仕入れて販売した。バザーは,1日目,2日目とも9時から15時まで実施された。
1日目の8時に,太郎さんのクラスへ,1日目と2日目で販売するペットボトル飲料とアイスクリームのすべてが届けられた。このとき,1日目に販売するドーナツも届けられた。また,2日目の8時に,2日目に販売するドーナツが届けられ,その個数は,1日目の8時に届けられたドーナツの個数の3倍であった。
ペットボトル飲料は,1日目と2日目で合計280本売れ,1日目に売れたペットボトル飲料の本数は,2日目に売れたペットボトル飲料の本数よりも130本少なかった。
1日目において,1日目の8時に届けられたドーナツはすべて売れた。1日目に売れたアイスクリームの個数は,1日目の8時に届けられたアイスクリームの個数の30%で,1日目に売れたドーナツの個数よりも34個多かった。
2日目は,アイスクリーム1個とドーナツ1個をセットにして販売することにした。1日目が終了した時点で残っていたアイスクリームの個数が,2日目の8時に届けられたドーナツの個数よりも多かったので,ドーナツはすべてセットにできたが,いくつかのアイスクリームはセットにできなかった。セットにできなかったアイスクリームは1個ずつで販売され,セットにしたアイスクリームとは別に4個が売れた。2日目が終了した時点で,アイスクリームは5個,ドーナツは3個残っていた。
これについて,次のア〜ウの問いに答えよ。
ア 1日目に売れたペットボトル飲料の本数は何本か。
【解説】
1日目に売れたペットボトル飲料の本数を \( x \) 本とすると,
2日目に売れたペットボトル飲料の本数は \( x+130 \) 本と表すことができます。
2日合計で280本売れたので,
\( x+x+130=280 \)
\( 2x=150 \)
\( x=75 \) (本)
イ 下線部について,1日目に届けられたアイスクリームの個数を \( x \) 個,1日目に届けられたドーナツの個数を \( y \) 個として,\( y \) を \( x \) を使った式で表せ。
【解説】
1日目に売れたアイスクリームの個数は,届けられたアイスクリームの個数の30%なので,\( 0.3x \) 個
1日目に届けられたドーナツはすべて売れたので,1日目に売れたドーナツの個数は \( y \) 個
1日目に売れたアイスクリームの個数は,1日目に売れたドーナツの個数よりも34個多かったので,
\( 0.3x=y+34 \)
\( y=0.3x-34 \)
ウ 1日目に届けられたアイスクリームの個数を \( x \) 個,1日目に届けられたドーナツの個数を \( y \) 個として,\( x,y \) の値を求めよ。\( x,y \) の値を求める過程も,式と計算を含めて書け。
【解答】
\( (x,y)=(480,110) \)
【解説】
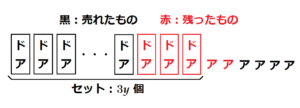
2日目に届けられたドーナツの個数は,1日目の3倍なので,\( 3y \) 個
ドーナツはすべてセットにできたので,2日目に用意したセットの個数も \( 3y \) 個
2日目終了時点で,ドーナツは3個残っていたので,残ったセットの個数も3個
2日目終了時点で,残っていたアイスクリーム5個のうち3個はセットにしていたものなので,
のこりの2個は単品で売っていたものです。単品で売れたアイスクリームは4個なので,
1日目に残ったアイスクリームの個数は,\( 3y+6 \) 個
これは,1日目に届けられたアイスクリームの個数の70%にあたるので,
\( 3y+6=0.7x \) ・・・ ➀
➀とイの式を連立方程式として解くと,
\( \left\{ \begin{array}{}
3y+6=0.7x \:\: ・・・ \:\: ➀ \\
y=0.3x-34 \:\: ・・・ \:\: ➁
\end{array} \right. \)
➀に➁を代入
\( 3(0.3x-34)+6=0.7x \)
\( 0.9x-102+6=0.7x \)
\( 0.2x=96 \)
\( x=480 \)
➁に代入
\( y=0.3 \times 480-34 \)
\( =110 \)
大問5
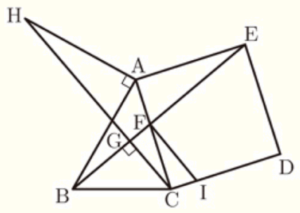
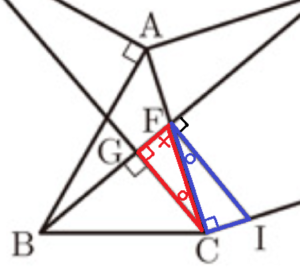
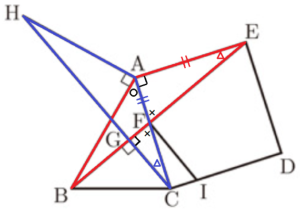
右の図のような,鋭角三角形 \( ABC \) があり,辺 \( AC \) を1辺にもつ正方形 \( ACDE \) を \( △ABC \) の外側につくる。辺 \( AC \) と線分 \( BE \) との交点を \( F \) とする。点 \( C \) から線分 \( BE \) に垂線をひき,その交点を \( G \) とする。点 \( A \) を通り,辺 \( AB \) に垂直な直線をひき,直線 \( CG \) との交点を \( H \) とする。また,点 \( F \) を通り,線分 \( GC \) に平行な直線をひき,辺 \( CD \) との交点を \( I \) とする。
このとき,次の(1) ,(2)の問いに答えなさい。
(1) \( △CFG \) ∽ \( △FIC \) であることを証明せよ。
【解答】
\( △CFG \) と \( △FIC \) において,
仮定より,\( ∠CGF=90° \) ・・・ ➀
正方形の内角はすべて \( 90° \) なので,\( ∠FCI=90° \) ・・・ ➁
➀➁より,\( ∠CGF=∠FCI \) ・・・ ➂
\( ∠FCG=180°-(∠CGF+∠CFG) \)
\( =90°-∠CFG \) ・・・ ➃
\( CG⊥BE,IF//CG \) より,\( IF⊥BE \)
\( ∠IFC=∠IFG-∠CFG \)
\( =90°-∠CFG \) ・・・ ➄
➃➄より,\( ∠FCG=∠IFC \) ・・・ ⑥
➂➅より,2組の角がそれぞれ等しいので,
\( △CFG \) ∽ \( △FIC \)
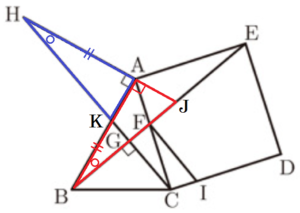
(2) 直線 \( AH \) と線分 \( BE \) との交点を \( J \),辺 \( AB \) と線分 \( CH \) との交点を \( K \) とする。このとき,\( BJ=HK \) であることを証明せよ。
【解答】
\( △ABE \) と \( △AHC \) において,
正方形の4辺はすべて等しいので,\( AE=AC \) ・・・ ➀
正方形の内角はすべて \( 90° \) なので,\( ∠EAC=90° \)
仮定より \( AB⊥AH \) なので,\( ∠EAC=∠BAH=90° \)
\( ∠BAE=∠EAC+∠BAC=90°+∠BAC \)
\( ∠HAC=∠BAH+∠BAC=90°+∠BAC \)
よって,\( ∠BAE=∠HAC \) ・・・ ➁
対頂角は等しいので,\( ∠AFE=∠GFC \)
\( CG⊥BE \) より,\( ∠CGF=90° \)
\( ∠AEF=180°-(∠EAF+∠AFE)=90°-∠AFE \)
\( ∠GCF=180°-(∠CGF+∠GFC)=90°-∠GFC \)
よって,\( ∠AEF=∠GCF \) ・・・ ➂
➀➁➂より,1組の辺とその両端の角がそれぞれ等しいので,
\( △ABE≡△AHC \)
対応する辺の長さと角の大きさは等しいので,
\( AB=AH \) ・・・ ④
\( ∠ABE=∠AHC \) ・・・ ➄
\( △ABJ \) と \( △AHK \) において,
仮定より \( AB⊥HJ \) なので,\( ∠HAK=∠BAJ \) ・・・ ⑥
④➄⑥より,1組の辺とその両端の角がそれぞれ等しいので,
\( △ABJ≡△AHK \)
対応する辺の長さは等しいので,\( BJ=HK \)