大問1
(1) \( 3-12+7 \) を計算しなさい。
【解説】
\( =-9+7 \)
\( =-2 \)
(2) \( 3(2a-b)-5(-a+2b) \) を計算しなさい。
【解説】
\( =6a-3b+5a-10b \)
\( =11a-13b \)
(3) \( 18xy^2 \div (-3y)^2 \) を計算しなさい。
【解説】
\( =\dfrac{18xy^2}{9y^2} \)
\( =2x \)
(4) 3つの数 \( \dfrac{3}{10},\dfrac{\sqrt{2}}{5},\dfrac{1}{\sqrt{10}} \) の大小を,不等号を使って表しなさい。
【解答】
\( \dfrac{\sqrt{2}}{5}<\dfrac{3}{10}<\dfrac{1}{\sqrt{10}} \)
【解説】
\( \dfrac{1}{\sqrt{10}} \) を有理化すると \( \dfrac{\sqrt{10}}{10} \) なので,
3つの数をそれぞれ10倍すると,
\( \dfrac{3}{10}=3=\sqrt{9},\dfrac{\sqrt{2}}{5}=2\sqrt{2}=\sqrt{8},\dfrac{\sqrt{10}}{10}=\sqrt{10} \)
となります。
\( \sqrt{8}<\sqrt{9}<\sqrt{10} \) なので,並べ替えると,
\( \dfrac{\sqrt{2}}{5}<\dfrac{3}{10}<\dfrac{1}{\sqrt{10}} \)
(5) 2次方程式 \( (x+5)^2=13 \) を解きなさい。
【解答】
\( x=-5±\sqrt{13} \)
【解説】
\( x+5=±\sqrt{13} \)
\( x=-5±\sqrt{13} \)
(6) 電子レンジで食品が温まるまでの時間は,電子レンジの出力に反比例する。ある食品の適切な加熱時間が \( 500 \; W \) の出力で \( 3 \) 分のとき,\( 600 \; W \) の出力での適切な加熱時間は何分何秒か,答えなさい。
【解答】
\( 2 \) 分 \( 30 \) 秒
【解説】
反比例を表す式は \( y=\dfrac{a}{x} \) なので,
電子レンジの出力を \( x \; W \),適切な加熱時間を \( y \) 分 とし,
\( x=500,y=3 \) を代入すると,
\( 3=\dfrac{a}{500} \)
\( a=1500 \)
となるので,
\( y=\dfrac{1500}{x} \) に \( x=600 \) を代入すると,
\( y=\dfrac{1500}{600}=\dfrac{5}{2}=2.5 \) (分)
\( 0.5 \) 分 \( =0.5 \times 60=30 \) 秒 なので,
\( 2.5 \) 分 \( =2 \) 分 \( 30 \) 秒
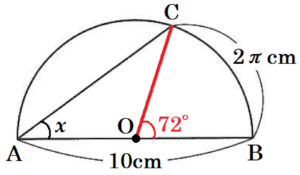
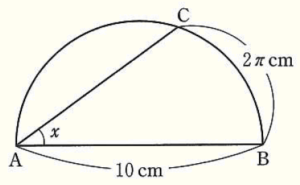
(7) 右の図のように,線分 \( AB \) を直径とする半円があり,\( AB=10 \; cm \) である。弧 \( AB \) 上に,弧 \( BC =2\pi{} \; cm \) となる点 \( C \) をとるとき,\( ∠x \) の大きさを答えなさい。
ただし,\( \pi{} \) は円周率である。
【解説】
この半円の弧の長さは
\( 10 \times \pi{} \times \dfrac{1}{2}=5\pi{} \; (cm) \)
なので,半円の中心を点 \( O \) とすると,
\( ∠BOC=180° \times \dfrac{2\pi{}}{5\pi{}}=72° \)
\( ∠BOC \) は弧 \( BC \) に対する中心角,
\( ∠BAC=∠x \) は弧 \( BC \) に対する円周角なので,
\( ∠x=\dfrac{1}{2}∠BOC=36° \)
(8) 箱の中に同じ大きさの白玉がたくさん入っている。標本調査を行い,この箱の中にある白玉の個数を推定することにした。この箱の中に,白玉と同じ大きさの赤玉 \( 300 \) 個を入れ,よくかき混ぜた後,箱の中から \( 100 \) 個の玉を取り出したところ,その中に赤玉が \( 10 \) 個あった。この箱の中には,およそ何個の白玉が入っていると推定されるか,答えなさい。
【解説】
よくかき混ぜた状態から標本(サンプル)を取り出しているので,
取り出した \( 100 \) 個の中での赤玉と白玉の比と全体の中での赤玉と白玉の比は等しくなると考えます。
取り出した \( 100 \) 個における赤玉と白玉の比は \( 10:90 \) なので,
箱の中の白玉の個数をおよそ \( x \) 個とすると,
\( 300:x=10:90 \)
\( x=2700 \)
大問2
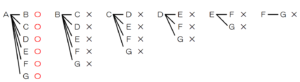
(1) 7人の生徒 A,B,C,D,E,F,G の中から,2人の代表をくじで選ぶとき,生徒Aが代表に選ばれる確率を求めなさい。
【解説】
2人を同時に選ぶときは「A・B」と「B・A」の組み合わせはまとめて1通りと考えることに注意して,
2人の選び方を樹形図で表し,Aを含むところに
○ をつけると,
Aを含む組み合わせは6通り,すべての組み合わせは21通りなので,
求める確率は \( \dfrac{6}{21}=\dfrac{2}{7} \)
(2) 関数 \( y=ax^2 \) について,\( x \) の値が \( 1 \) から \( 4 \) まで増加するときの変化の割合が \( 2a^2 \) である。
このとき,\( a \) の値を求めなさい。ただし,\( a≠0 \) とする。
【解答】
\( a=\dfrac{5}{2} \)
【解説】
\( x=1 \) のときの \( y \) の値は,\( y=a \times 1^2=a \),
\( x=4 \) のときの \( y \) の値は,\( y=a \times 4^2=16a \)
なので,変化の割合は,
\( \dfrac{16a-a}{4-1}=2a^2 \)
\( 5a=2a^2 \)
\( a(2a-5)=0 \)
\( a=\dfrac{5}{2} \) ( \( a≠0 \) より)
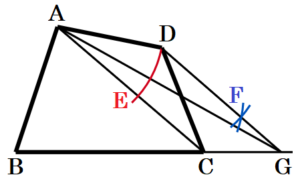
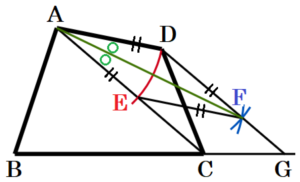
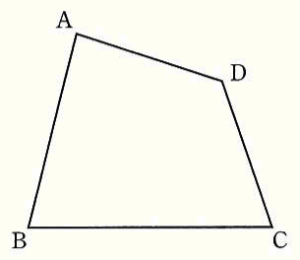
(3) 右の図のような,四角形 \( ABCD \) がある。この四角形と面積が等しい三角形を,定規とコンパスを用いて,1つ作図しなさい。ただし,作図は解答用紙に行い,作図に使った線は消さないで残しておくこと。
【解答】
手順1 線分 \( AC \) を描く
手順2 辺 \( BC \) を延長した直線を描く
手順3 点 \( A \) を中心に,辺 \( AD \) を半径とする
円弧を描く
(線分 \( AC \) との交点を点 \( E \) とします。)
手順4 2点 \( D,E \) を中心に,辺 \( AD \) を半径と
する円弧を描く
(交点を点 \( F \) とします。)
手順5 2点 \( D,F \) を通る直線を描く
(手順2の直線との交点を点 \( G \) とします。)
手順6 線分 \( AG \) を描く
この図において,\( △ABG \) が求める三角形になります。
【解説】
【どんな三角形を書けばいい?】
四角形 \( ABCD \) は \( △ABC \) と \( △ACD \) を
くっつけたものなので,
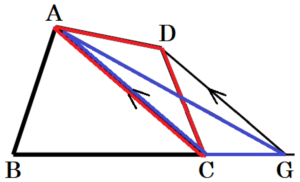
点 \( D \) を通り,線分 \( AC \) と平行な直線と
辺 \( BC \) を延長した線との交点を点 \( G \) とすると,
等積変形の考え方から,
\( △ACD=△ACG \) となります。
このとき,四角形 \( ABCD \) と\( △ABG \) の面積は等しくなります。
つまり,点 \( D \) を通り,線分 \( AC \) と平行な直線を描けばいいことになります。
【 どうしたら \( AC//DG \) となる直線が描ける?】
ひし形(平行四辺形)の向かい合う辺は平行になることから,
線分 \( AC \) 上に点 \( E \) を持つような,ひし形 \( AEFD \) をつくることで
\( AC//DG \) となる直線を描いていきます。
ひし形のすべての辺の長さは等しいので,
点 \( A \) を中心に,辺 \( AD \) を半径とする
円弧を描くことで, \( AE=AD \) となるような
点 \( E \) を作れます。
また,ひし形の対角線は角の二等分線になるので,
2点 \( D,E \) を中心に,辺 \( AD \) を半径とする円弧を描くことで,交点 \( F \) はひし形 \( AEFD \) の頂点になります。
ひし形(平行四辺形)の向かい合う辺は平行なので,\( DF//AE \) であり,
辺 \( DF \) の延長線上に点 \( G \) をとると,\( AC//DG \) になります。
大問3
下の図1,2のように,1辺の長さが \( 6 \; cm \) の正三角形 \( ABC \) と,1辺の長さが \( 5 \; cm \) の正三角形 \( DEF \) がある。このとき,次の(1),(2)の問いに答えなさい。
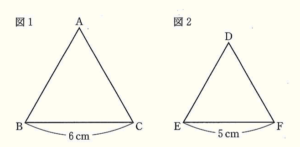
(1) 正三角形 \( ABC \) と正三角形 \( DEF \) の面積の比を答えなさい。
【解説】
相似な三角形の面積比は,相似比の2乗の比になるので,
\( △ABC:△DEF=6^2:5^2=36:25 \)
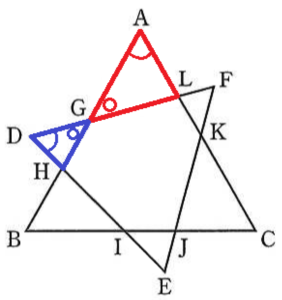
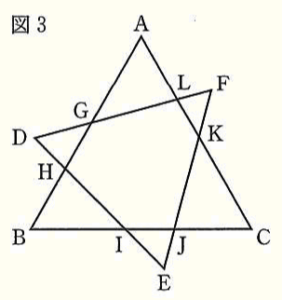
(2) 右の図3のように,正三角形 \( DEF \) を 頂点 \( D,E,F \) がすべて正三角形 \( ABC \) の周の外側にくるように,正三角形 \( ABC \) に重ねる。辺 \( DF,DE \) と辺 \( AB \) との交点をそれぞれ \( G,H \) とし,辺 \( ED,EF \) と辺 \( BC \) との交点をそれぞれ \( I, J \) とする。また,辺 \( FE,FD \) と辺 \( CA \) との交点をそれぞれ \( K,L \) とする。このとき,次の ①,② の問いに答えなさい。
➀ \( △AGL \) ∽ \( △DGH \) であることを証明しなさい。
【解答】
\( △AGL \) と \( △DGH \) において
対頂角は等しいので,\( ∠AGL=∠DGH \) ・・・ ➀
どちらも正三角形の内角なので,
\( ∠GAL=∠GDH=60° \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △AGL \) ∽ \( △DGH \)
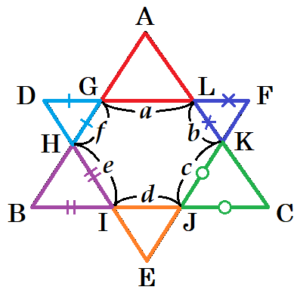
② 辺 \( BC \) と辺 \( DF \) が平行であるとき,六角形 \( GHIJKL \) の周の長さを求めなさい。
【解説】
\( GL=a,LK=b,JK=c,IJ=d \),
\( HI=e,HG=f \) とすると,
六角形 \( GHIJKL \) の周の長さは
\( a+b+c+d+e+f \) と表すことができます。
\( △AGL,△FLK,△CKJ,△EJI \),
\( △BIH,△DHG \) はすべて正三角形なので,
\( DG=HG=f,LF=LK=b \),
\( BI=HI=e,JC=JK=c \) であり,
\( f+a+b=DF=5 \; (cm) \) ・・・ ➀
\( e+d+c=BC=6 \; (cm) \) ・・・ ➁
➀ \( + \) ➁ すると,
\( a+b+c+d+e+f=11 \; (cm) \)
大問4
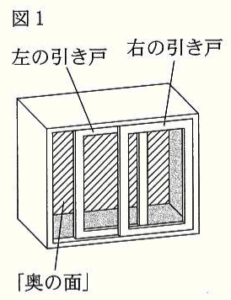
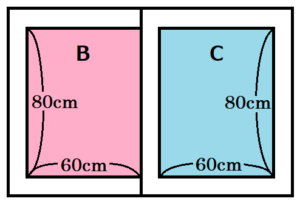
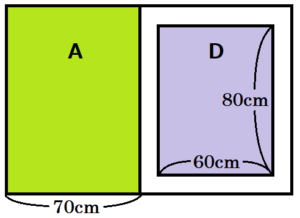
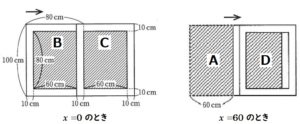
右の図1のような,左右2枚の引き戸がついた棚がある。この棚の内側の面のうち, の面を「奥の面」と呼ぶことにする。2枚の引き戸は,形と大きさが同じであり,それぞれが下の図2のように,透明なガラス板と枠でできている。2枚の引き戸をすべて閉めて,正面から見ると,図3のように,枠が重なり,ガラス板を通して「奥の面」が見える。また,このとき,2枚の引き戸はそれぞれ,全体が縦 \( 100 \; cm \),横 \( 80 \; cm \) の長方形に,ガラス板が縦 \( 80 \; cm \),横 \( 60 \; cm \) の長方形に,枠の幅が \( 10 \; cm \) に見える。
の面を「奥の面」と呼ぶことにする。2枚の引き戸は,形と大きさが同じであり,それぞれが下の図2のように,透明なガラス板と枠でできている。2枚の引き戸をすべて閉めて,正面から見ると,図3のように,枠が重なり,ガラス板を通して「奥の面」が見える。また,このとき,2枚の引き戸はそれぞれ,全体が縦 \( 100 \; cm \),横 \( 80 \; cm \) の長方形に,ガラス板が縦 \( 80 \; cm \),横 \( 60 \; cm \) の長方形に,枠の幅が \( 10 \; cm \) に見える。
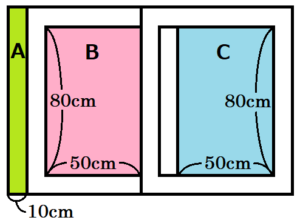
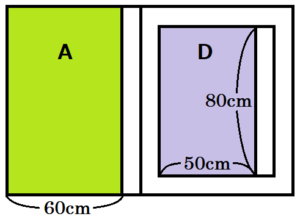
図3の状態から,左の引き戸だけを右向きに動かす。図4~6は,左の引き戸を右向きに動かしたときのようすを順に表したものであり,2枚の引き戸を正面から見たときに見える「奥の面」を,A~Dのように分類する。
左の引き戸を,図3の位置から右向きに動かした長さを \( x \; cm \) とするとき,あとの(1)~(5)の問いに答えなさい。 ただし,\( 0≦x≦70 \) とする。
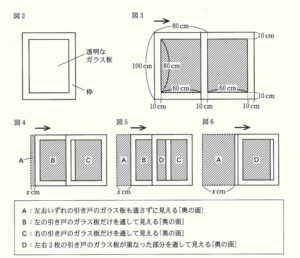
(1) \( x=15 \) のとき,Aの面積を答えなさい。
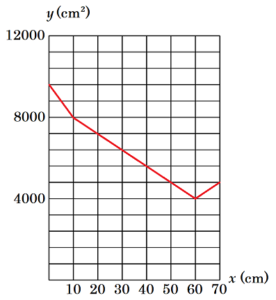
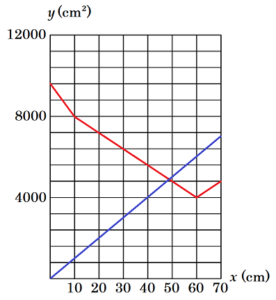
(2) 次の文は,左の引き戸を,図3の位置から右向きに動かした長さと,2枚の引き戸を正面から見たときに見える「奥の面」の面積の関係について述べたものの一部である。このとき,文中の ア に当てはまるものを,A~Dからすべて選び,その符号を書きなさい。
左の引き戸を,図3の位置から右向きに動かした長さと,
ア の面積の関係をグラフに表すと,
下の図7のようになる。
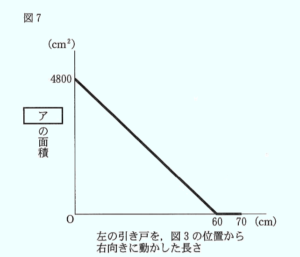
【解説】
図3が \( x=0 \) のときを表していて,
A,
Dの面積は \( 0 \; cm^2 \) なので,あてはまりません。
また,このとき,
B,
Cの面積は \( 80 \times 60=4800 \; (cm^2) \) なので,あてはまります。
次に,\( x=60 \) のときの図を描いてみると,B,Cの面積は \( 0 \; cm^2 \) なので,これもあてはまります。
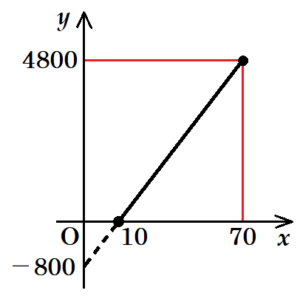
(3) \( 10≦x≦70 \) のとき,Dの面積を \( x \) を用いて表しなさい。
【解説】
\( 10≦x≦70 \) のときのDの面積を \( y \; cm^2 \) とすると,
\( x=10 \) のとき,\( y=0 \)
\( x=70 \) のとき,\( y=4800 \)
となるので,
この直線の式を \( y=ax+b \) とすると,
\( a=\dfrac{4800-0}{70-10}=80 \)
\( y=80x+b \) に \( x=10,y=0 \) を代入すると,
\( 0=80 \times 10+b \)
\( b=-800 \)
であり,この直線の式は,\( y=80x-800 \)
よって,Dの面積は \( 80x-800 \)
(4) 3つの部分B,C,Dの面積の和を \( y \; cm^2 \) とするとき,\( x \) と \( y \) の関係を表すグラフをかきなさい。
【解説】
【 \( x=0 \) のとき】
右の図のとおり,
Bの面積 \( =80 \times 60=4800 \; (cm^2) \)
Cの面積 \( =80 \times 60=4800 \; (cm^2) \)
Dの面積 \( =0 \; (cm^2) \)
なので,
合計の面積は \( y=4800+4800+0=9600 \; (cm^2) \)
このとき,左の引き戸の枠の右側と右の引き戸の左側が重なっています。
ここから,左の引き戸を動かすと,図5のように左の引き戸の枠の右側も見えるようになり,
左の引き戸を \( 10cm \) 動かすごとに,
B,Cの面積は \( 80 \times 10=800 \; (cm^2) \) ずつ小さくなっていきます。
これは,\( x=10 \) の位置まで続きます。
【 \( x=10 \) のとき】
右の図のとおり,
Bの面積 \( =80 \times 50=4000 \; (cm^2) \)
Cの面積 \( =80 \times 50=4000 \; (cm^2) \)
Dの面積 \( =0 \; (cm^2) \)
なので,
合計の面積は \( y=4000+4000+0=8000 \; (cm^2) \)
さらに左の引き戸を動かすと,図5のようにDの部分が現れ,
左の引き戸を \( 10cm \) 動かすごとに,
B,Cの面積は \( 80 \times 10=800 \; (cm^2) \) ずつ小さくなり,
Dの面積は \( 80 \times 10=800 \; (cm^2) \) ずつ大きくなっていきます。
これは,\( x=60 \) の位置まで続きます。
【 \( x=60 \) のとき】
右の図のとおり,
Bの面積 \( =0 \; (cm^2) \)
Cの面積 \( =0 \; (cm^2) \)
Dの面積 \( =80 \times 50=4000 \; (cm^2) \)
なので,
合計の面積は \( y=0+0+4000=4000 \; (cm^2) \)
さらに左の引き戸を動かすと,右の引き戸の左側で隠れていたガラスの部分が見えてくるので,
Dの面積はさらに大きくなっていきます。
これは,\( x=70 \) の位置まで続きます。
【 \( x=70 \) のとき】
右の図のとおり,
Bの面積 \( =0 \; (cm^2) \)
Cの面積 \( =0 \; (cm^2) \)
Dの面積 \( =80 \times 60=4800 \; (cm^2) \)
なので,
合計の面積は \( y=0+0+4800=4800 \; (cm^2) \)
以上より,左の引き戸を \( 10cm \) 動かすごとにB,C,Dの面積は,それぞれ \( 800 \; cm^2 \) ずつ
大きくなったり小さくなったりしているので,
求めるグラフは,\( (x,y)=(0,9600),(10,8000),(60,4000),(70,4800) \) の4点を
直線で結んだものになります。
(5) Aの面積と,3つの部分B,C,Dの面積の和が等しいとき,\( x \) の値を求めなさい。
【解答】
\( x=\dfrac{440}{9} \)
【解説】
左の引き戸を \( 10cm \) 動かすごとに,
Aの面積は \( 100 \times 10=1000 \; (cm^2) \) ずつ大きくなっていきます。
これを(4)のグラフに書き加えると,
下の図のようになります。
\( 10≦x≦60 \) の範囲において,
赤の直線の式を \( y=ax+b \) とすると,
\( a=\dfrac{4000-8000}{60-10}=-80 \)
\( y=-80x+b \) に \( x=10,y=8000 \) を代入すると,
\( 8000=-80 \times 10+b \)
\( b=8800 \)
ここから,
赤の直線の式は \( y=-80x+8800 \) ・・・ ➀
青の直線の式は \( y=100x \) ・・・ ➁ なので,
➀➁を連立方程式として解くと,
\( -80x+8800=100x \)
\( 180x=8800 \)
\( x=\dfrac{440}{9} \)
大問5
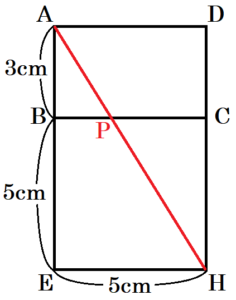
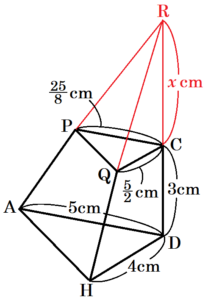
下の図のように,\( AB=3 \; cm,AD=5 \; cm,BF=4 \; cm \) の直方体 \( ABCD-EFGH \) がある。辺 \( BC \) 上を点 \( B \) から点 \( C \) まで移動する点を \( P \) とし,点 \( P \) を通り線分 \( AH \) に平行な直線と辺 \( CG \) との交点を \( Q \) とする。このとき,次の(1)~(3)の問いに答えなさい。
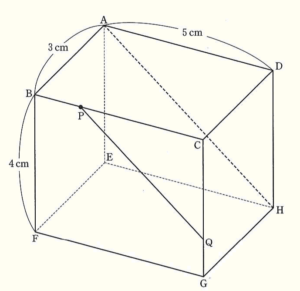
(1) 線分 \( BE \) の長さを答えなさい。
【解説】
\( △BFE \) は,\( EF=AB=3 \; cm,BF=4 \; cm,∠BFE=90° \) の直角三角形なので,
\( EF:BF:BE=3:4:5 \) であり,\( BE=5 \; cm \)
(2) 四角形 \( BCHE \) の面積を答えなさい。
【解説】
四角形 \( BCHE \) は,\( BC=AD=5 \; cm,BE=5 \; cm \) の正方形なので,
面積は,\( 5 \times 5=25 \; (cm^2) \)
(3) \( AP+PH \) の長さが最も短くなるとき,次の①,②の問いに答えなさい。
① 線分 \( BP \) の長さを求めなさい。
【解答】
\( \dfrac{15}{8} \; cm \)
【解説】
線分 \( PH \) は,面 \( BCHE \) 上にあるので,
面 \( ABCD \) と面 \( BCHE \) を展開してできる
長方形 \( AEHD \) において,
3点 \( A,P,H \) が一直線上に並ぶとき,
\( AP+PH \) の長さが最も短くなります。
\( BP//EH \) なので,\( △ABP \) ∽ \( △AEH \) であり,
\( AB=3 \; cm,BE=5 \; cm,EH=AD=5 \; cm \) より,
\( BP:EH=AB:AE \)
\( BP:5=3:8 \)
\( BP=\dfrac{15}{8} \; (cm) \)
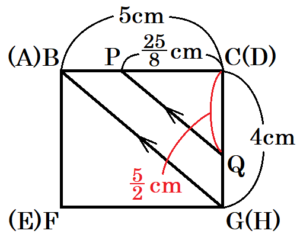
➁ 6点 \( P,Q,C,A,H,D \) を結んでできる立体の体積を求めなさい。
【解答】
\( \dfrac{645}{32} \; cm^3 \)
【解説】
四角形 \( BFGC \) と四角形 \( AEHD \) を重ね合わせて考えると,\( PQ//AH \) より,
\( △PQC \) ∽ \( △AHD \) となっています。
\( PC=BC-BP=5-\dfrac{15}{8}=\dfrac{25}{8} \; (cm) \) なので,
\( CQ:DH=PC:AD \)
\( CQ:4=\dfrac{25}{8}:5 \)
\( CQ=\dfrac{5}{2} \; (cm) \)
\( △PQC \) ∽ \( △AHD \) より,
\( AP,HQ,DC \) の延長線は1点で交わります。
この交点を点 \( R \) とし,\( RC=x \; cm \) とすると,
\( PQ//AH \) より,\( △RPC \) ∽ \( △RAD \) なので,
\( RC:RD=PC:AD \)
\( x:x+3=\dfrac{25}{8}:5 \)
\( x:x+3=5:8 \)
\( 8x=5(x+3) \)
\( x=5 \; (cm) \)
求める立体の体積は,「三角すい \( RPQC \; – \) 三角すい \( RAHD \) 」で求められるので,
三角すい \( RPQC=\left( \dfrac{5}{2} \times \dfrac{25}{8} \times \dfrac{1}{2} \right) \times 5 \times \dfrac{1}{3}=\dfrac{625}{96} \; (cm^3) \)
三角すい \( RAHD=\left( 4 \times 5 \times \dfrac{1}{2} \right) \times 8 \times \dfrac{1}{3}=\dfrac{80}{3} \; (cm^3) \)
よって,求める立体の体積は,\( \dfrac{80}{3}-\dfrac{625}{96}=\dfrac{645}{32} \; (cm^3) \)

![]() の面を「奥の面」と呼ぶことにする。2枚の引き戸は,形と大きさが同じであり,それぞれが下の図2のように,透明なガラス板と枠でできている。2枚の引き戸をすべて閉めて,正面から見ると,図3のように,枠が重なり,ガラス板を通して「奥の面」が見える。また,このとき,2枚の引き戸はそれぞれ,全体が縦 \( 100 \; cm \),横 \( 80 \; cm \) の長方形に,ガラス板が縦 \( 80 \; cm \),横 \( 60 \; cm \) の長方形に,枠の幅が \( 10 \; cm \) に見える。
の面を「奥の面」と呼ぶことにする。2枚の引き戸は,形と大きさが同じであり,それぞれが下の図2のように,透明なガラス板と枠でできている。2枚の引き戸をすべて閉めて,正面から見ると,図3のように,枠が重なり,ガラス板を通して「奥の面」が見える。また,このとき,2枚の引き戸はそれぞれ,全体が縦 \( 100 \; cm \),横 \( 80 \; cm \) の長方形に,ガラス板が縦 \( 80 \; cm \),横 \( 60 \; cm \) の長方形に,枠の幅が \( 10 \; cm \) に見える。