大問1
問1 \( 5+3 \times (-2) \) を計算しなさい。
【解説】
\( =5+(-6) \)
\( =5-6 \)
\( =-1 \)
問2 \( 8a \times 3b^2 \div 12ab \) を計算しなさい。
【解説】
\( =\dfrac{8a \times 3b^2}{12ab} \)
\( =2b \)
問3 連立方程式 \( \left\{ \begin{array}{}
x-4y=1 \\
2x-5y=8 \\
\end{array} \right. \) を解きなさい。
【解説】
\( \left\{ \begin{array}{}
x-4y=1 \;\; ・・・ \;\; ➀ \\
2x-5y=8 \;\; ・・・ \;\; ➁ \\
\end{array} \right. \)
➀ \( \times 2 \) すると,
\( 2x-8y=2 \) ・・・ ➀’
➁ \( – \) ➀’すると,
\( 3y=6 \)
\( y=2 \)
➀に代入すると,
\( x-4 \times 2=1 \)
\( x-8=1 \)
\( x=9 \)
問4 \( y \) は \( x \) に反比例し,\( x=4 \) のとき \( y=2 \) である。比例定数を求めなさい。
【解説】
反比例を表す式は \( y=\dfrac{a}{x} \)(\( a \) は比例定数)です。
この式に \( x=4,y=2 \) を代入すると,
\( 2=\dfrac{a}{4} \)
\( 8=a \)
問5 \( △ABC \) と \( △DEF \) において,\( AB=DE \) である。このとき,条件として加えても \( △ABC≡△DEF \) がいつも成り立つとは限らないものを,ア~エから1つ選び,記号で答えなさい。
ア \( BC=EF,AC=DF \)
イ \( BC=EF,∠C=∠F \)
ウ \( BC=EF,∠B=∠E \)
エ \( ∠A=∠D,∠B=∠E \)
【解説】
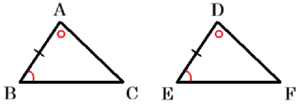
三角形の合同条件を満たしていないのはイになります。
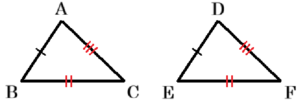
ア 3組の辺がそれぞれ等しい
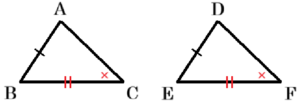
イ 三角形の合同条件を満たしていない
ウ 2組の辺とその間の角がそれぞれ等しい
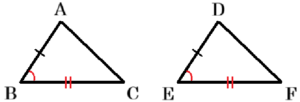
エ 1組の辺とその両端の角がそれぞれ等しい
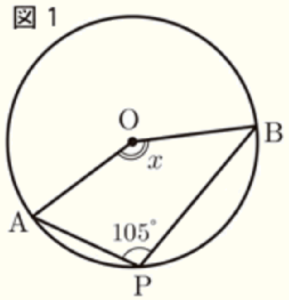
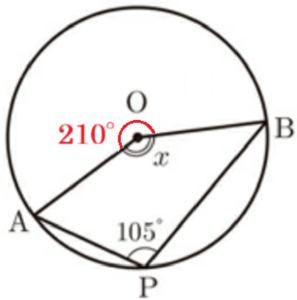
問6 図1のように,半径が \( 6 \; cm \) の円 \( O \) の円周上に3点 \( A,B,P \) があり,\( ∠APB=105° \) である。次の1,2に答えなさい。
1 図1の \( ∠x \) の大きさを求めなさい。
【解説】
\( ∠APB \) は \( \stackrel{\huge\frown}{ AB } \)(点 \( P \) を含まない方)に対する円周角,
\( ∠AOB \) は \( \stackrel{\huge\frown}{ AB } \)(点 \( P \) を含まない方)に対する中心角なので,
\( ∠AOB=2 \times 105°=210° \)
よって,
\( ∠x=360°-210°=150° \)
2 点 \( P \) を含む \( \stackrel{\huge\frown}{ AB } \) の長さは何 \( cm \) か,求めなさい。
【解答】
\( \stackrel{\huge\frown}{ AB }=5\pi{} \; cm \)
【解説】
おうぎ形の弧の長さは中心角の大きさに比例するので,
\( \stackrel{\huge\frown}{ AB } \;\; =2\pi{} \times 6 \times \dfrac{150°}{360°} \)
\( =5\pi{} \; (cm) \)
問7 図2は,縦横同じ \( n \) 個のマス目が左右に印刷された,作文を書くための用紙である。次の1,2に答えなさい。ただし,マス目は用紙のおもて面だけに印刷され,マス目1つに1字書くとする(句読点,記号も1字として考える)。
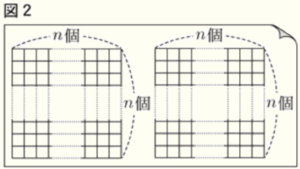
1 \( n=20 \) のとき,用紙1枚に最大何字まで書くことができるか,求めなさい。
【解説】
縦横同じ \( 20 \) 個のマス目のかたまりが2つあるので,マス目の個数は,
\( 20 \times 20 \times 2=800 \)(個)
よって,書ける文字数は最大 \( 800 \) 個になります。
2 1枚に \( 1000 \) 字書くことが可能な用紙のうち,最も小さい \( n \) の値を求めなさい。
【解説】
1の結果から,1枚に書くことが可能な文字数は \( 2n^2 \) と表すことができます。
1枚に \( 1000 \) 字書くことが可能な用紙には,\( 1000 \) 個以上のマス目があればいいので,
\( 2n^2≧1000 \)
\( n^2≧500 \)
\( n≧10\sqrt{5} \)
\( \sqrt{5}=2.236 \) と近似できるので,
\( n≧10\sqrt{5} \; (=22.36) \)
縦横に並ぶマス目の数 \( n \) は整数になるので,
あてはまる最も小さい \( n \) の値は \( 23 \) になります。
問8 アルミ缶とスチール缶の空き缶を合わせて \( 2000 \) 個回収した。回収した空き缶の中から \( 100 \) 個を無作為に抽出したところ,スチール缶が \( 40 \) 個含まれていた。回収したアルミ缶の個数はおよそ何個と推定されるか。ア~エから最も適当なものを1つ選び,記号で答えなさい。
ア \( 800 \) 個 イ \( 1000 \) 個 ウ \( 1200 \) 個 エ \( 1400 \) 個
【解説】
標本調査では,母集団に含まれる調査対象の割合は
抽出した標本(サンプル)に含まれる調査対象の割合と等しくなります。
回収したスチール缶の個数を \( x \) 個とすると,
\( 2000:x=100:40 \)
\( 2000:x=5:2 \)
\( 5x=2000 \times 2 \)
\( x=800 \)(個)
よって,回収したアルミ缶の個数は \( 2000-800=1200 \)(個)になります。
大問2
問1 袋の中に1~9の整数が1つずつ書かれた9個の玉がある。この袋から玉を1個取り出すとき,次の1,2に答えなさい。ただし,どの玉が取り出されることも同様に確からしいとする。
1 取り出した玉に書かれた数が素数である確率を求めなさい。
【解説】
素数とは,「1
とその数自身以外に約数を持たない自然数」のことです。
1~9の整数のうち素数は「2,3,5,7」の4つなので,
(1は約数が1だけなので,素数ではありません)
その確率は \( \dfrac{4}{9} \) になります。
2 取り出した玉に書かれた数を \( x^2+ax-6=0 \) の \( a \) に代入して二次方程式をつくるとき,次の(1),(2)に答えなさい。
(1) 玉に書かれた数が5のとき,二次方程式の解を求めなさい。
【解説】
玉に書かれた数が5のとき,二次方程式は,\( x^2+5x-6=0 \) なので,
\( x^2+5x-6=0 \)
\( (x-1)(x+6)=0 \)
\( x=1,-6 \)
(2) 二次方程式の解が整数となる確率を求めなさい。
【解説】
二次方程式の解が整数になるのは,この二次方程式が
\( (x+m)(x+n)=0 \; (m,n \) は整数)
の形に因数分解できるときです。
【 \( a=1 \) のとき,】
二次方程式は,\( x^2+x-6=0 \) なので,
\( x^2+x-6=0 \)
\( (x-2)(x+3)=0 \)
【 \( a=2 \) のとき,】
二次方程式は,\( x^2+2x-6=0 \) で,
\( (x+m)(x+n)=0 \;\; (m,n \) は整数) の形に因数分解できないので,
解は整数になりません。
【 \( a=3 \) のとき,】
二次方程式は,\( x^2+3x-6=0 \) で,
\( (x+m)(x+n)=0 \;\; (m,n \) は整数) の形に因数分解できないので,
解は整数になりません。
【 \( a=4 \) のとき,】
二次方程式は,\( x^2+4x-6=0 \) で,
\( (x+m)(x+n)=0 \;\; (m,n \) は整数) の形に因数分解できないので,
解は整数になりません。
【 \( a=5 \) のとき,】
二次方程式は,\( x^2+5x-6=0 \) なので,
\( x^2+5x-6=0 \)
\( (x-1)(x+6)=0 \)
【 \( a=6 \) のとき,】
二次方程式は,\( x^2+6x-6=0 \) で,
\( (x+m)(x+n)=0 \;\; (m,n \) は整数) の形に因数分解できないので,
解は整数になりません。
【 \( a=7 \) のとき,】
二次方程式は,\( x^2+7x-6=0 \) で,
\( (x+m)(x+n)=0 \;\; (m,n \) は整数) の形に因数分解できないので,
解は整数になりません。
【 \( a=8 \) のとき,】
二次方程式は,\( x^2+8x-6=0 \) で,
\( (x+m)(x+n)=0 \;\; (m,n \) は整数) の形に因数分解できないので,
解は整数になりません。
【 \( a=9 \) のとき,】
二次方程式は,\( x^2+9x-6=0 \) で,
\( (x+m)(x+n)=0 \;\; (m,n \) は整数) の形に因数分解できないので,
解は整数になりません。
以上より,二次方程式の解が整数となるのは,\( a=1,5 \) のときの2通りなので,
その確率は \( \dfrac{2}{9} \) になります。
問2 太郎さんと先生が整数の性質について話している。次の1,2に答えなさい。ただし, ア にはすべて同じ数が入る。
1 次の会話文1を読んで,後の(1),(2)に答えなさい。
会話文1
先生:連続する整数にはいろいろな性質があります。どんなものがありましたか。
太郎:(自分のノートを見返す)
はい。「連続する3つの整数の和は ア の倍数になる」ことを確かめたときのノートが残っていました。
太郎さんのノート
連続する3つの整数のうち,真ん中の数を \( n \) と表すと,連続する3つの整数は,
\( n-1,n,n+1 \)
と表される。
これらの数の和は,
\( (n-1)+n+(n+1)=3n \)
\( n \) は整数なので,\( 3n \) は ア の倍数になる。
したがって,連続する3つの整数の和は ア の倍数になる。
(1) ア にあてはまる数を答えなさい。
【解説】
\( 3n \) は \( 3 \) の整数倍なので,3の倍数であるといえます。
(2) 連続する3つの整数の和が \( 2025 \) のとき,連続する3つの整数を求めなさい。
【解説】
太郎さんのノートの結果から,
\( 3n=2025 \)
\( n=675 \)
よって,連続する3つの整数のうち真ん中が \( 675 \) なので,
残りの2つは \( 674 \) と \( 676 \) になります。
2 次の会話文2を読んで,後の(1),(2)に答えなさい。
会話文2
先生:ところで,連続する3つの整数をそれぞれ2乗して和を求めるとどうなりますか。
太郎:具体的に選んだ数でためしてみると,表のようになりました。
ア の倍数にはなりそうにないです。
先生:2乗の和に1をたすとどうですか。
太郎:表の場合は ア の倍数になりました。
いつも成り立つのかな。
先生:それでは,「連続する3つの整数の2乗の和に1をたした数は
ア の倍数になる」ことを証明してみましょう。
\( \phantom{ } \)
\( \phantom{ } \)
\( \phantom{ } \)
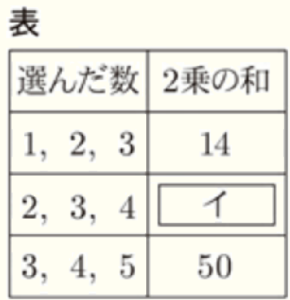
証明
連続する3つの整数のうち,真ん中の数を \( n \) と表すと,連続する3つの整数は,
\( n-1,n,n+1 \)
と表される。
これらの数の2乗の和に1をたすと,
ウ
したがって,連続する3つの整数の2乗の和に1をたした数は ア の倍数になる。
(1) 表中の イ にあてはまる数を答えなさい。
【解説】
\( 2^2+3^2+4^2=4+9+16 \)
\( =29 \)
(2) ウ に証明の続きを書き入れ,証明を完成しなさい。ただし, ウ にあてはまる部分のみ書くこと。
【解答】
\( (n-1)^2+n^2+(n+1)^2+1=(n^2-2n+1)+n^2+(n^2+2n+1)+1 \)
\( =3n^2+3 \)
\( =3(n^2+1) \)
\( n \) は整数なので,\( n^2+1 \) も整数である。
ここから,\( 3(n^2+1) \) は3の倍数になる。
大問3
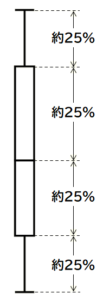
問1 町役場では,よりよい交通サービスを提供するため,ある路線のバスの利用状況を調査した。図1は平日 \( 20 \) 日間分の各時間帯におけるバス利用者数のデータを箱ひげ図に表したものである。後の1~3に答えなさい。
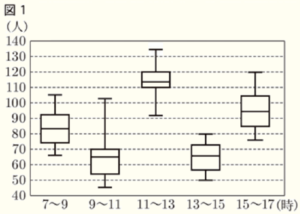
1 図1の箱ひげ図のうち,範囲が最も小さい時間帯はどれか。ア~オから1つ選び,記号で答えなさい。
ア \( 7~9 \) 時 イ \( 9~11 \) 時 ウ \( 11~13 \) 時 エ \( 13~15 \) 時 オ \( 15~17 \) 時
【解説】
範囲は 最大値 \( – \) 最小値 で求められます。
また,箱ひげ図(縦書き)では,
ひげの上端から下端までの長さ
が範囲を表しています。
各時間帯でのおよその範囲は,
\( 7~9 \) 時 ・・・ \( 115-67=48 \)(人)
\( 9~11 \) 時 ・・・ \( 111-45=66 \)(人)
\( 11~13 \) 時 ・・・ \( 134-91=43 \)(人)
\( 13~15 \) 時 ・・・ \( 80-50=30 \)(人)
\( 15~17 \) 時 ・・・ \( 120-77=43 \)(人)
であり,範囲が最も小さい時間帯は,
\( 13~15 \) 時になります。
2 \( 9~11 \) 時の時間帯について,利用者数が \( 70 \) 人以上の日は何日あったと考えられるか。考えられる最も少ない日数を求めなさい。
【解説】
\( 9~11 \) 時の時間帯の箱ひげ図では,第三四分位数が \( 70 \) 人になっています。
全部で \( 20 \) 日間分のデータなので,第三四分位数は,
少ない方から15番目と16番目の平均値(多い方から5番目と6番目の平均値)
になります。
第三四分位数が \( 70 \) 人であることから,
少ない方から15番目(多い方から6番目)の値は \( 70 \) 以下,
少ない方から16番目(多い方から5番目)の値は \( 70 \) 以上
の値になっています。
少ない方から15番目(多い方から6番目)の値が \( 70 \) より小さい場合は,
\( 70 \) 以上の値になるのは5個,
少ない方から15番目(多い方から6番目)の値が \( 70 \) である場合は,
\( 70 \) 以上の値になるのは6個以上
なので,考えられる最も少ない日数は5日になります。
3 図1から,町役場の田中さんは,混雑することが多いと予想される \( 11~13 \) 時の時間帯にバスを増便する提案をした。田中さんの発言の ① , ➁ にあてはまる適切な言葉をそれぞれ答えなさい。
田中さんの発言
図1から,\( 11~13 \) 時の時間帯をほかと比べると,中央値が ① こと,四分位範囲が ➁ ことがわかります。この2つのことから,\( 11~13 \) 時の時間帯にバスを増便することを提案します。
【解答】
① ・・・ 最も大きい
➁ ・・・ 最も小さい
【解説】
他の時間帯に比べて中央値が大きいことから,全体的に他の時間よりも利用人数が多いと推測できます。
また,四分位範囲はデータのばらつきを示して
おり,値が小さいほどばらつきが少ないと
考えられます。
さらに,箱ひげ図では四分位範囲は箱の長さとして表されており,全体の約半数のデータを含んでいます。
\( 11~13 \) 時の時間帯の中央値(約 \( 113 \) 人)は
もっとも大きく,
さらに,四分位範囲が小さい(箱の長さが短い)ことから,約半数の日数(10日間)の利用者数が
\( 110 \) 人以上 \( 120 \) 人以下であることがわかります。
他の時間帯では,利用者数が \( 110 \) 人以上であったのは,\( 15~17 \) 時の時間帯の5日以下だけと
わかるので,\( 11~13 \) 時の時間帯の利用者がもっとも多いと判断できます。
問2 町役場では,駅 \( A \) から観光地 \( B \) までの \( 3600 \; m \) のまっすぐな路線に,自動運転の車 \( P,Q \) の運行計画を立てることにした。車 \( P,Q \) は次のルールで走行し,同じ路線を走るとする。車 \( P \) が最初に駅 \( A \) を出発してから経過した時間を \( x \) 分, 車 \( P,Q \) から駅 \( A \) までの距離を \( y \; m \) として,\( x \) と \( y \) の関係をグラフに表すと図2のようになった。後の1~3に答えなさい。
【車 \( P \) のルール】
・最初は駅 \( A \) を出発し,走行中は一定の速さで走り,駅 \( A \) と観光地 \( B \) の間を2往復する。
・駅 \( A \),観光地 \( B \) に到着したときは,それぞれ \( 1 \) 分間停車する。
【車 \( Q \) のルール】
・車 \( P \) が駅 \( A \) を最初に出発してから \( 10 \) 分後に駅 \( A \) を出発する。
・走行中は一定の速さで走り,駅 \( A \) と観光地 \( B \) の間を1往復する。ただし,速さは車 \( P \) と
異なる。
・観光地 \( B \) に到着したときは,\( 4 \) 分間停車する。
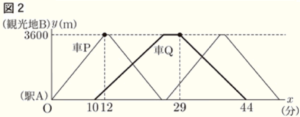
1 車 \( P \) について, 次の(1),(2)に答えなさい。
(1) 車 \( P \) の走行中の速さは分速何 \( m \) か,求めなさい。
【解説】
グラフより,駅 \( A \) から観光地 \( B \) までの \( 3600 \; m \) を \( 12 \) 分で走行するので,
\( 3600 \div 12=300 \; (m) \)
(2) 車 \( P \) が2回目に駅 \( A \) を出発するときの,\( x \) の値を求めなさい。
【解説】
グラフから,観光地 \( B \) に到着するのは,\( x=12 \) のとき,
観光地 \( B \) で \( 1 \) 分間停車するので,観光地 \( B \) を出発するのは \( x=13 \) のとき,
観光地 \( B \) から駅 \( A \) に到着するまでに \( 12 \) 分かかるので,駅 \( A \) に到着するのは \( x=25 \) のとき,
駅 \( A \) で \( 1 \) 分間停車するので,2回目に駅 \( A \) を出発するのは \( x=26 \) のとき
になります。
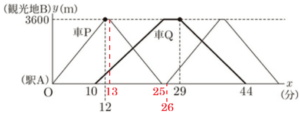
2 車 \( Q \) が駅 \( A \) から観光地 \( B \) に向かうとき,\( y \) を \( x \) の式で表しなさい。ただし,変域は求めなくてよい。
【解説】
グラフから,車 \( Q \) が観光地 \( B \) を出発するのは \( x=29 \) のときで,
車 \( Q \) は観光地 \( B \) で \( 4 \) 分間停車するので,
車 \( Q \) が観光地 \( B \) に到着するのは \( x=25 \) のときです。
ここから,車 \( Q \) のグラフは \( (10,0),(25,3600) \) を通るので,
この直線の式を \( y=ax+b \) とすると,
\( a=\dfrac{3600-0}{25-10}=240 \)
\( y=240x+b \) に \( x=10,y=0 \) を代入すると,
\( 0=240 \times 10+b \)
\( b=-2400 \)
よって,\( y=240x-2400 \)
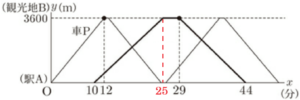
3 車 \( P \) と車 \( Q \) が1回目にすれ違うときの,\( y \) の値を求めなさい。
【解説】
車 \( P \) が観光地 \( B \) から駅 \( A \) に向かうときを表す式を \( y=-300x+n \) とし,
\( x=25,y=0 \) を代入すると,
\( 0=-300 \times 25+n \)
\( n=7500 \)
なので,\( y=-300x+7500 \)
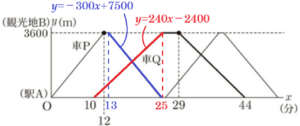
2直線の交点は2つの式の連立方程式の解として表されるので,
\( 240x-2400=-300x+7500 \)
\( 540x=9900 \)
\( x=\dfrac{55}{3} \)
\( y=240x-2400 \) に \( x=\dfrac{55}{3} \) を代入すると,
\( y=240 \times \dfrac{55}{3}-2400 \)
\( =2000 \)
大問4
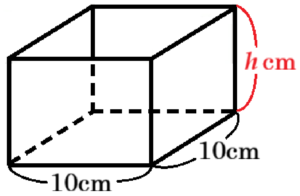
昔から使われている体積を表す単位に合があり,しょうゆや酢などを量るときに用いられている。体積を合で量るときは,升と呼ばれるふたのない容器が使われ,内側が底面を正方形とする直方体になっている。図1は5合入る升で5合升といい,\( 900 \; cm^3 \) の水がちょうど入るとする。次の問1~問3に答えなさい。
問1 図1の5合升の内側は,底面の1辺の長さが \( 10 \; cm \) である。内側の高さは何 \( cm \) か,求めなさい。
【解説】
5合升の内側を表す直方体を右の図のように表し,
内側の高さを \( h \; cm \) すると,
\( 10 \times 10 \times h=900 \)
\( h=9 \; (cm) \)
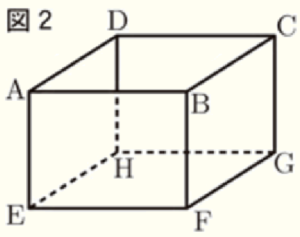
問2 図2のように,図1の5合升の内側の各頂点を \( A~H \) とする。底面 \( EFGH \) が水平な状態で升に水がいっぱいに入っているとき,後の1,2に答えなさい。
1 升を傾け水をこぼしていったところ,升に残った水の体積がちょうど半分になった。升内の水面はどの頂点を通っていると考えられるか,ア〜ウから1つ選び,記号で答えなさい。
ア 頂点 \( A,B,C,D \) イ 頂点 \( A,C,G,E \) ウ 頂点 \( A,D,G,F \)
【解説】
升を傾け水をこぼしていくとき,水面は常に水平な状態になります。
これに注意して,升を傾けた状態とそのときの水面を図に表すと,
【面 \( ABCD \) が水平になるとき】
図2の状態そのままで,升に水がいっぱい入ったままの状態なので,あてはまりません。
\( \phantom{ } \)
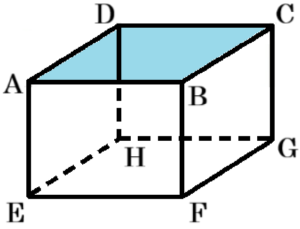
【面 \( ACGE \) が水平になるとき】
面 \( A,C,D \) にあたる部分から水がこぼれてしまうので,升内の水面が4点 \( A,C,G,E \) を通る状態で維持することはできません。
\( \phantom{ } \)
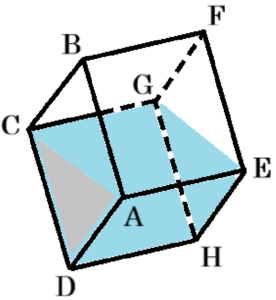
【面 \( ADGF \) が水平になるとき】
水は,三角柱 \( AEF-DHG \) の形になります。
\( AF,DG \) は長方形 \( AEFB \) の対角線なので,\( △AEF \) の面積は長方形 \( AEFB \) の面積の \( \dfrac{1}{2} \)
\( DG \) は長方形 \( DHGC \) の対角線なので,\( \) ,\( △DHG \) の面積は長方形 \( DHGC \) の面積の \( \dfrac{1}{2} \)
なので,升に残った水の体積はちょうど半分になります。
\( \phantom{ } \)
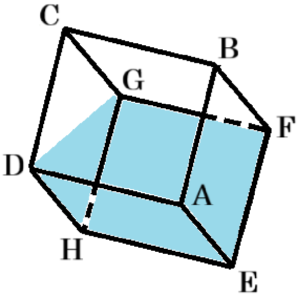
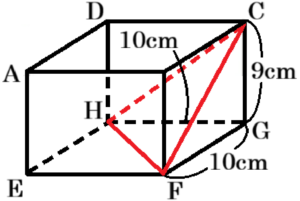
2 頂点 \( C \) から水をこぼしながら水面が頂点 \( C,H,F \) を通るまで升を傾けたとき,残った水の体積は何 \( cm^3 \) か求めなさい。
【解説】
図2に面 \( CHF \) を書き加えると,残った水の部分は,
三角すい \( C-FGH \) の形になっているので,その体積は,
\( \left( 10 \times 10 \times \dfrac{1}{2} \right) \times 9 \times \dfrac{1}{3}=150 \; (cm^3) \)
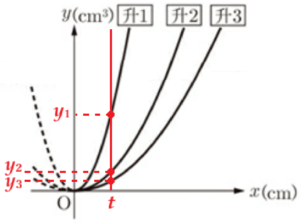
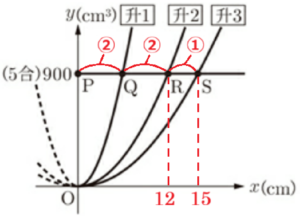
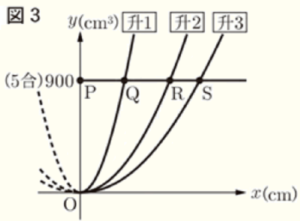
問3 内側の高さが異なる 升1,升2,升3について,内側の底面の1辺の長さを \( x \; cm \),それぞれの升に水をいっぱいに入れたときの水の体積を \( y \; cm^3 \) として調べ,\( x \) と \( y \) の関係をグラフに表すと図3のような3本の放物線になった。また,体積が5合を示す直線 \( y=900 \) と,\( y \) 軸および 升1,升2,升3を表す放物線とが交わる点をそれぞれ \( P,Q,R,S \) とする。後の1,2に答えなさい。
1 内側の高さが最も高いのはどの升か,ア〜ウから1つ選び,記号で答えなさい。
ア 升1 イ 升2 ウ 升3
【解説】
升1において,内側の底面の1辺の長さを \( x=t \; cm \),内側の高さを \( h_1 \; cm \),
水をいっぱいに入れたときの水の体積を \( y_1 \; cm^3 \),
升2において,内側の底面の1辺の長さを \( x=t \; cm \),内側の高さを \( h_2 \; cm \),
水をいっぱいに入れたときの水の体積を \( y_2 \; cm^3 \),
升3において,内側の底面の1辺の長さを \( x=t \; cm \),内側の高さを \( h_3 \; cm \),
水をいっぱいに入れたときの水の体積を \( y_3 \; cm^3 \)
とすると,
それぞれの升の内側の底面の1辺の長さと
水をいっぱいに入れたときの水の体積の関係は,
升1 ・・・ \( y_1=t^2 \times h_1 \) → \( h_1=\dfrac{y_1}{t^2} \)
升2 ・・・ \( y_2=t^2 \times h_2 \) → \( h_2=\dfrac{y_2}{t^2} \)
升3 ・・・ \( y_3=t^2 \times h_3 \) → \( h_3=\dfrac{y_3}{t^2} \)
と表すことができます。
グラフから,\( y_1>y_2>y_3 \) なので,\( \dfrac{y_1}{t^2}>\dfrac{y_2}{t^2}>\dfrac{y_3}{t^2} \) になります。
よって,\( h_1>h_2>h_3 \) になります。
2 升3の内側の高さが \( 4 \; cm \) のとき,次の(1),(2)に答えなさい。
(1) 点 \( S \) の \( x \) 座標を求めなさい。
【解説】
升3において,\( x \) と \( y \) の関係式は,\( y=4x^2 \) になります。
点 \( S \) の \( y \) 座標は \( 900 \) なので,
\( 900=4x^2 \)
\( x^2=225 \)
\( x=15 \; (cm) \)(\( x>0 \) より)
(2) \( PQ:QR:RS=2:2:1 \) のとき,升2の内側の高さは何 \( cm \) か,求めなさい。
【解答】
\( \dfrac{25}{4} \; cm \)
【解説】
(1)より,点 \( S \) の \( x \) 座標は \( 15 \) なので,
点 \( R \) の \( x \) 座標は \( 15 \times \dfrac{4}{5}=12 \) です。
升2の内側の高さを \( h_2 \; cm \) とすると,
升2の \( x \) と \( y \) の関係式は \( y=h_2 \times x^2 \) なので,
\( x=12,y=900 \) を代入すると,
\( 900=h_2 \times 12^2 \)
\( h_2=\dfrac{25}{4} \; (cm) \)
になります。
大問5
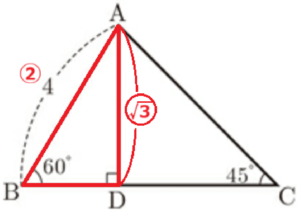
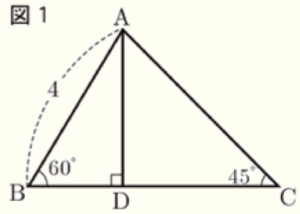
図1のように, \( AB=4,∠B=60°,∠C=45° \) の \( △ABC \) において,点 \( A \) から辺 \( BC \) に引いた垂線と辺 \( BC \) との交点を \( D \) とする。後の問1,問2に答えなさい。
問1 次の1,2に答えなさい。
1 線分 \( AD \) の長さを求めなさい。
【解説】
\( △ABD \) は \( 30°,60°,90° \) の直角三角形なので,
\( AB:AD=2:\sqrt{3} \)
\( 4:AD=2:\sqrt{3} \)
\( 2AD=4\sqrt{3} \)
\( AD=2\sqrt{3} \)
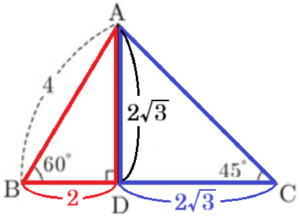
2 \( △ABC \) の面積を求めなさい。
【解説】
\( △ABD \) において,
\( AB:BD=2:1 \)
\( 4:BD=2:1 \)
\( BD=2 \)
\( △ACD \) は直角二等辺三角形なので,
\( AD=DC=2\sqrt{3} \)
よって,\( △ABC \) の面積は,
\( (BD+DC) \times AD \times \dfrac{1}{2}=(2+2\sqrt{3}) \times 2\sqrt{3} \times \dfrac{1}{2} \)
\( =(2+2\sqrt{3}) \times \sqrt{3} \)
\( =6+2\sqrt{3} \)
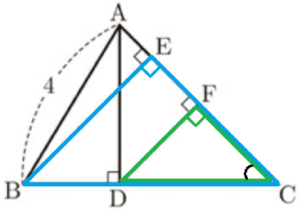
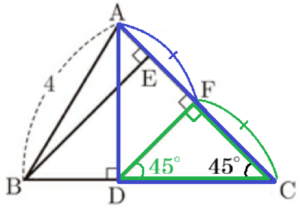
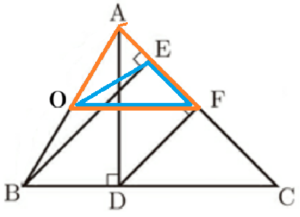
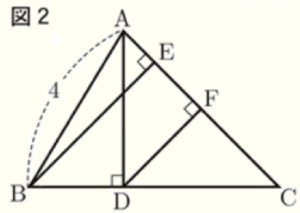
問2 図2のように,点 \( B \) と点 \( D \) から辺 \( AC \) に引いた垂線と辺 \( AC \) との交点をそれぞれ \( E,F \) とする。後の1,2に答えなさい。
1 \( △CFD \) ∽ \( △CEB \) であることを証明しなさい。
【解答】
\( △CFD \) と \( △CEB \) において,
共通な角なので,\( ∠DCF=∠BCE \) ・・・ ➀
仮定より,\( ∠CFD=∠CEB=90° \) ・・・ ➁
➀➁より,2組の角がそれぞれ等しいので,
\( △CFD \) ∽ \( △CEB \)
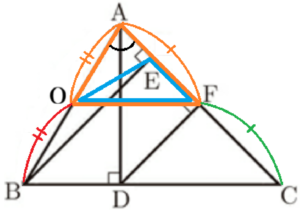
2 3点 \( A,B,E \) を通る円の中心を \( O \) とする。次の(1)~(3)に答えなさい。
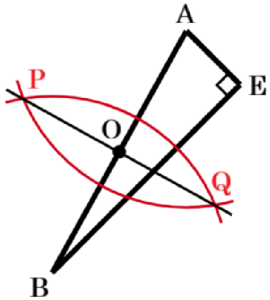
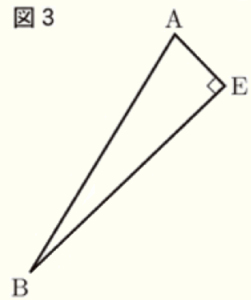
(1) 点 \( O \) を図3に作図して求めなさい。また,点 \( O \) の位置を示す文字 \( O \) も図の中に書き入れなさい。ただし,作図にはコンパスと定規を用い,作図に用いた線は消さないでおくこと。
【解答】
手順1 2点 \( A,B \) を中心に円弧を描く。
(交点を \( P,Q \) とします)
手順2 2点 \( P,Q \) を通る直線を描く。
手順2の直線と辺 \( AB \) の交点が
求める点 \( O \) になります。
【解説】
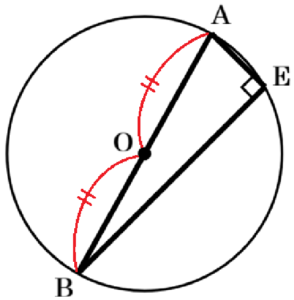
右の図のように3点 \( A,B,E \) を通る円を描くと,
\( ∠AEB \) は \( \stackrel{\huge\frown}{ AB } \) に対する円周角になっていて,
\( ∠AEB=90° \) であることから、
線分 \( AB \) はこの円の直径になります。
よって,この円の中心 \( O \) は,線分 \( AB \) の中点になります。
このことから,線分 \( AB \) の垂直二等分線を描くことによって,線分 \( AB \) の中点を求めることができます。
(2) 線分 \( OF \) の長さを求めなさい。
【解説】
\( ∠CDF=45°,∠ADC=90° \) であることから,
線分 \( DF \) は \( ∠ADC \) の二等分線です。
\( △ACD \) は直角二等辺三角形なので,
線分 \( DF \) と辺 \( AC \) の交点 \( F \) は
辺 \( AC \) の中点になっています。
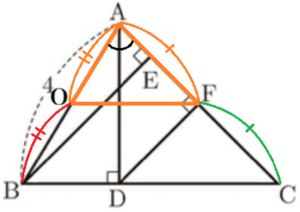
(1)より,点 \( O \) は辺 \( AB \) の中点なので,
\( AO:AB=AF:AC=1:2 \),
\( ∠AOF=∠BOC \),
であり,
2組の辺の比とその間の角がそれぞれ等しいので,
\( △AOF \) ∽ \( △ABC \)
対応する辺の比は等しいので,\( OF:BC=1:2 \)
問1の2より,\( BD=2,DC=2\sqrt{3} \) なので,
\( OF=\dfrac{1}{2}(BD+DC) \)
\( =\dfrac{1}{2}(2+2\sqrt{3}) \)
\( =1+\sqrt{3} \)
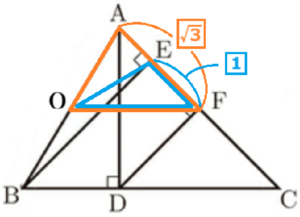
(3) \( △EOF \) の面積を求めなさい。
【解答】
\( △EOF=\dfrac{1+\sqrt{3}}{2} \)
【解説】
\( △AOF \) の底辺を \( AF \),\( △EOF \) の底辺を \( EF \) とすると,高さが共通なので,
\( △AOF \) と \( △EOF \) の面積比は \( EF:AF \) と等しくなります。
ここから,\( △AOF \) の面積と \( AF:EF \) を
求めることができれば,\( △EOF \) の面積を求めることができます。
【\( △AOF \) の面積を求める】
相似な三角形の面積比は相似比の2乗の比と等しくなります。
(2)より,\( △AOF \) と \( △ABC \) の相似比は \( 1:2 \) なので,、面積比は,
\( △AOF:△ABC=1^2:2^2=1:4 \)
問1の2より,\( △ABC=6+2\sqrt{3} \) なので,
\( △AOF:(6+2\sqrt{3})=1:4 \)
\( 4△AOF=6+2\sqrt{3} \)
\( △AOF=\dfrac{3+\sqrt{3}}{2} \)
\( \phantom{ } \)
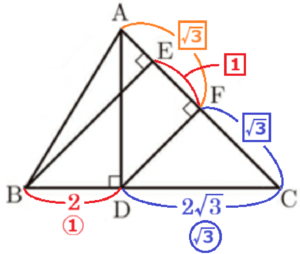
【\( EF:AF \) を求める】
\( △CFD \) ∽ \( △CEB \),\( BD=2,DC=2\sqrt{3} \)
なので,
\( EF:FC=BD:DC=1:\sqrt{3} \)
また,点 \( F \) は辺 \( AC \) の中点なので,
\( EF:AF=EF:FC=1:\sqrt{3} \)
\( \phantom{ } \)
以上より,
\( △EOF:△AOF=1:\sqrt{3} \)
\( △EOF:\dfrac{3+\sqrt{3}}{2}=1:\sqrt{3} \)
\( \sqrt{3}△EOF=\dfrac{3+\sqrt{3}}{2} \)
\( △EOF=\dfrac{1+\sqrt{3}}{2} \)
大問A










-300x246.png)